Разработка программного обеспечения для реализации модели пористых структур на основе трехпериодических поверхностей

Теория минимальных поверхностей уже давно стала предметом математических исследований (см., например, обзоры [1; 2]). Эта теория является объектом изучения для различных разделов математики: комплексного анализа, вариационных принципов, дифференциальной геометрии, топологии, теории дифференциальных уравнений в частных производных, теории геометрических мер и других [2; 3]. В последнее время появился практический интерес к минимальным поверхностям и другим трехпериодическим поверхностям, в частности с точки зрения их механических свойств [4; 5].

Для разработки общих методов построения трехпериодических и минимальных поверхностей большое значение имеет серия работ [6–9]. В данных статьях используется тот факт, что трехпериодические минимальные поверхности делят трехмерное пространство на два непересекающихся конгруэнтных лабиринта, и способы построения таких поверхностей изучаются с точки зрения их свойств симметрии. Симметрии поверхности описываются группой G, которая является полной группой пространственных симметрий поверхности, и некоторой ее подгруппой H с индексом 2, которая не перемешивает данные лабиринты при соответствующих преобразованиях. Далее в работах [6–9] использовались известные кристаллографические группы в качестве G-H групп, и на их основе была построена серия трехпериодических минимальных поверхностей. Существуют и другие примеры построения трехпериодических и минимальных поверхностей [1; 2], тем не менее можно сказать, что в настоящее время не найдены общие методы генерации трехпериодических и минимальных поверхностей в трехмерном пространстве.

В данной работе мы предлагаем оригинальный обобщенный подход получения трехпериодических поверхностей, идея которого восходит к работам [6–9]. Наш подход основан на алгоритме получения трехпериодических поверхностей на основе их природных аналогов – кристаллов.

В качестве исходного инструмента используется известный в мире комплекс программ ToposPro [10; 11], который позволяет анализировать и определять топологическую и геометрическую структуру кристаллов. В частности, он может выделять отдельные структурные единицы решетки – тайлы и на их основе собирать элементарные ячейки кристаллов в виде каркасов. Так, на основе кристаллографических решеток т. н. цеолитов ToposPro строит элементарную ячейку трехмер-

ьи^^™, © Смольков М.И., Крутов А.Ф., 2022

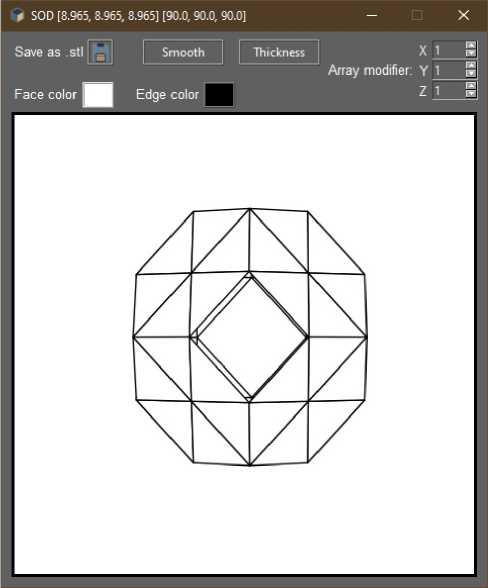
Рис. 1. Окно приложение TPS Extractor с открытым каркасом SOD

Fig. 1. TPS Extractor application window with SOD framework open ной периодической поверхности. После удаления некоторых граней и открытия каналов элементарная ячейка принимает форму пористого скелета, образованного плоскими многоугольниками, – каркаса. Задача настоящей статьи заключается в разработке программного обеспечения для реализации модели пористых структур на основе сгенерированных в ToposPro каркасов различного топологического типа. Для получения трехмерной периодической поверхности с системой бесконечных непересекающихся лабиринтов необходимо сшить элементарные ячейки на границах. С этой целью была написана процедура трансляции элементарной ячейки, реализованная в разработанной в данной статье программе TPS Extractor.

Для получения гладкой поверхности из каркаса необходимо провести процедуру сглаживания. Эта процедура также реализована в созданной программе. В качестве параметра, определяющего качество сглаживания, мы выбрали так называемую среднюю кривизну, которая для минимальных поверхностей равна нулю в каждой точке поверхности. Таким образом, трехмерная периодическая поверхность будет представлять собой совокупность сшитых вместе малых элементарных поверхностей нулевой средней кривизны.

• 1.    Программное обеспечение для моделирования пористого материала на основе трехпериодических поверхностей

• 2.    Форматы входных и выходных файлов

Для получения трехпериодических поверхностей и моделирования пористых материалов на основе полученных в ToposPro каркасов было разработано программное обеспечение – TPS Extractor, позволяющее преобразовывать извлеченные из ToposPro каркасы, сохраненные в формате .t3g, в формат .stl или stereolithography – широко используемый формат для хранения трехмерных моделей объектов. Информация об объекте хранится как список треугольников, которые описывают его поверхность, и их нормалей. Этот формат является наиболее подходящим для печати этих каркасов на 3D-принтерах. Каркас, построенный с помощью ToposPro, представляет собой набор граней (колец) разного типа. Каждое кольцо – это набор точек с координатами вершин данного кольца в пространстве.

Извлеченные из ToposPro каркасы представляют собой текстовый файл формата .t3g, пример которого представлен ниже:

1 AFG : 3D surface formed by rings: 4a, 6a, 6c, 6d, 6f 2 12.54800 12.54800 20.78900

• 3    90.00 90.00 120.00

• 4    RING 4 a

• 5    0.08890 0.67060 0.37460

• 6    0.00350 0.75340 0.25000

• 7    0.24660 0.99650 0.25000

• 8    0.32940 0.91110 0.37460

• 9    ...

• –    Строка 1 содержит название каркаса (AFG), и все уникальные цепи атомов – кольца (4a, 6a, 6c, 6d, 6f);

• –    Строки 2 и 3 – параметры атомной ячейки: длина, ширина и высота ограничивающего параллелепипеда, а также углы его наклона относительно осей X, Y, Z;

• –    Строка 4 из ключевого слова RING и его типа (4 a);

• –    Строки с 5 по 8 – координаты атомов, составляющих замкнутую цепочку;

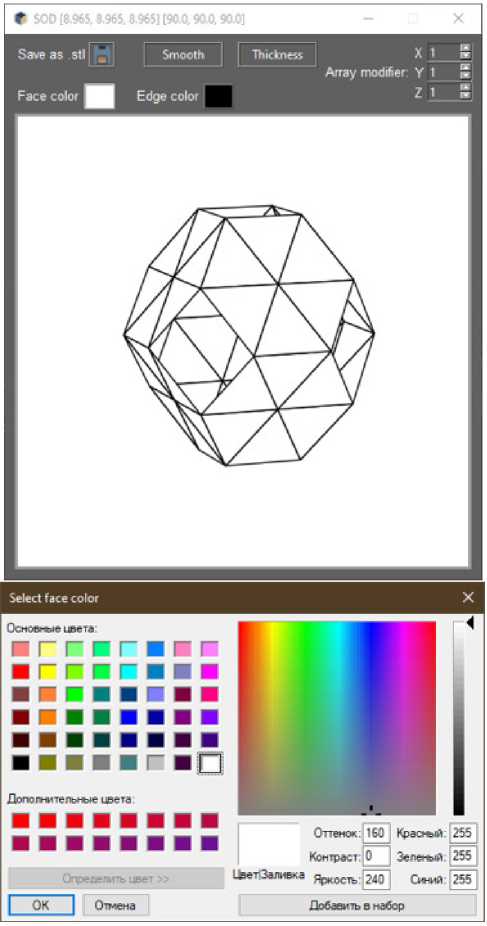
Рис. 2. Меню выбора цвета фасетов или граней созданной модели

Fig. 2. Menu for selecting the color of facets or faces of the created model

• –    Оставшиеся строчки аналогичны строкам с 4 по 8 для оставшихся колец.

На основе полученных данных разработанное приложение строит трехмерную модель каркаса, например содалита (SOD), как показано на рис. 1.

На рис. 1 также представлен интерфейс разработанного приложения. В заголовке окна описаны название каркаса (SOD) и параметры атомной ячейки.

Алгоритм конвертации из .t3g в .stl следующий:

Входной файл: набор колец из точек с координатами в пространстве.

• 1)    Считываем .t3g файл и сохраняем имя каркаса (цеолита) и параметры атомной ячейки.

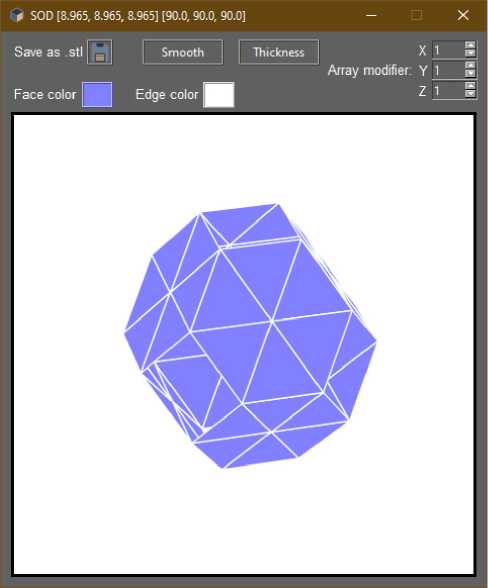
Рис. 3. Результат изменения цвета

Fig. 3. Color change result

• 2)    По метке ключевого слова RING считываем k координатных строк k вершин данного кольца.

• 3)    Производим триангуляцию, находя центроид данного кольца. Координатами центроида кольца является среднее арифметическое координат его вершин. Создаем набор из k треугольников, отбирая точки обходя вершины кольца против часовой стрелки, причем каждая вторая точка в наборе – центроид кольца. В дальнейшем каждый треугольник из такого набора будем называть фасетом.

• 4)    Полученный набор сохраняем для дальнейшего преобразования в некоторый массив данных.

• 5)    Повторяем пункты 2, 3, 4 до конца файла.

• 6)    Каждые координаты сохраненных наборов приводим к параметрам атомной ячейки, сохраненной прежде.

• 7)    Формируем файл формата .stl согласно общепризнанному стандарту.

Выходной файл: STL-формат каркаса.

Параметр k в данном алгоритме равен количеству вершин кольца.

Разработанный графический интерфейс предоставляет возможности просмотра (вращение и увеличение масштаба) созданной 3D-модели, а также для удобства просмотра имеются возможности цветовой настройки фасетов и граней фигуры, как показано на рис. 2, 3.

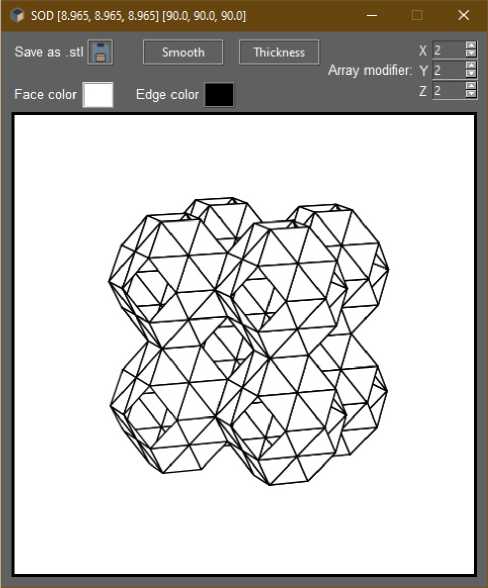
Рис. 4. Пример трансляции каркаса SOD

Fig. 4. Example of SOD framework translation

Созданное приложение также позволяет сохранять полученную модель в файлы формата .stl. В разработанной программе присутствует конвертация в два типа формата файла STL:

• •    Бинарный – файл формата Binary .stl представляет собой особую структуру:

Заголовок в UINT8 – первые 80 байт, которые обычно игнорируются; используется для записи требуемой информации о модели;

Число треугольников в UINT32;

Для каждого фасета:

Координаты нормали фасета в REAL[32];

Координаты вершины №1 фасета в

REAL[32];

Координаты вершины №2 фасета в

REAL[32];

Координаты вершины №3 фасета в

REAL[32];

Количество байт в UINT16

Конец файла

• •    ASCII – файл формата ASCII .stl представляет собой особую структуру:

Метка начала файла и название модели

(необязательно)

Нормаль фасета и ее координаты

Начало фасета №1

Вершина №1 фасета и ее координаты

Вершина №2 фасета и ее координаты

Вершина №3 фасета и ее координаты

Конец фасета №1

Метка конца файла.

Для конвертации из формата .t3g, полученного с помощью программы ToposPro, в формат .stl были написаны алгоритм триангуляции и алгоритм расчета нормалей по правилу правой руки.

Алгоритм триангуляции производит разбиение полигонов полученного каркаса на фасеты и рассчитывает для них нормали с помощью алгоритма в соответствии с требованиями формата .stl: вектор нормали направлен наружу, вершины перечислены в порядке появления против часовой стрелки. Каркас в данном формате будет использоваться для печати на 3D-принтере.

3. Трансляция и сглаживание

Как было сказано ранее, для получения трехмерной периодической поверхности с системой каналов необходимо сшить элементарные ячейки на границах. Для этого была написана процедура трансляции.

В пространстве параллельный перенос в прямоугольной системе координат ( x , y , z ) выражается аналитически при помощи:

(x, y, z) ^ (x + a, y + b, z + c), где вектор MM1 = (a, b, c) вычисляется из параметров элементарной ячейки. Пример трансляции представлен на рис. 4.

Для создания процедуры сглаживания необходимо было решить проблемы подсчета средней кривизны для триуангулированных поверхностей и способ минимизации средней кривизны.

Подсчет средней кривизны был реализован с использованием результатов работы [12]. Для подтверждения работоспособности, написанного алгоритма был произведен численный эксперимент.

Для подтверждения правильности вычисления значения средней кривизны были созданы 120 экземпляров икосфер с разными радиусами. Пример икосферы представлен на рис. 5.

Известно, что средняя кривизна сферы в каждой точке равна константе и вычисляется по формуле:

H = R?

где R – радиус сферы.

Результаты теоретического и численного расчета средней кривизны представлены в таблице.

Рис. 5. Пример икосферы

Fig. 5. Example of an icosphere

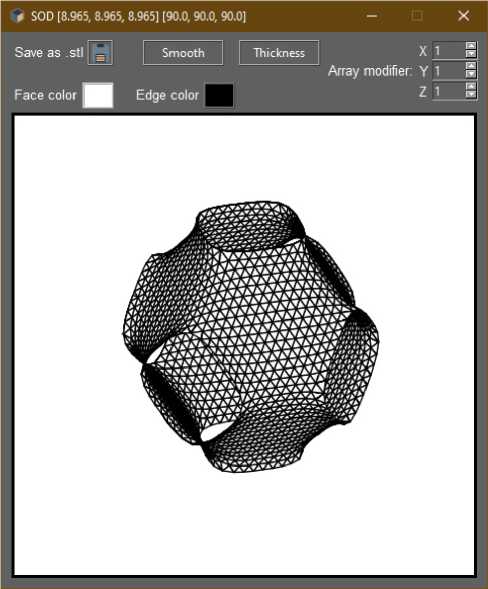
Рис. 6. Сглаженная трехпериодическая поверхность, полученная из каркаса SOD

Fig. 6. Smoothed three-period surface obtained from the SOD framework

Из представленных в таблице результатов видно, что разработанный численный алгоритм является приемлемым для расчета средней кривизны.

На основе расчета средней кривизны был разработан алгоритм сглаживания трехмерной поверхности.

Образец задания процедуры сглаживания: _smooth (mesh, n, min_angle, iterations) , где mesh – несглаженный каркас; n – количество разбиений каркаса, выбирается пользователем; min_angle – минимальный желательный угол между смежными гранями каркаса, при идеальном ва-

Таблица. Расчет средней кривизны Table. Average curvature calculation

Значение H R Теоретическое Расчетное Разница 0,1 10 10,000128 1,20Е-05 0,2 5 5,000064 1,20Е-05 0,3 3,(3) 3,333376 1,20Е-05 0,4 2,5 2,500032 1,20Е-05 0,5 2 2,000032 1,3Е-05 0,6 1,(6) 1,666688 1,28Е-05 0,7 1,428 1,428658 6,06Е-05 0,8 1,25 1,249199 0,0006408 0,9 1,(1) 1,111061 4,51Е-05 1,0 1 0,999959 4,1Е-05 1,1 0,9(09) 0,908746 0,0003794 1,2 0,8(3) 0,833295 4,6Е-0,5 1,3 0,769 0,769249 2,37Е-05 1,4 0,714 0,714027 0,0003622 1,5 0,(6) 0,666636 4,6Е-05 1,6 0,625 0,627276 0,0036416 1,7 0,588 0,590166 0,0032822 1,8 0,(5) 0,556464 0,0016352 1,9 0,526 0,527584 0,0024096 2,0 0,5 0,500731 0,0014620 рианте равен 180 градусам; iterations – количество повторений операций смещения точек смежных граней с углом неравным min_angle.

Алгоритм сглаживания заключается в следующем:

• 1)    Разбиваем фигуру на большее количество треугольников в n раз.

• 2)    Ищем точки смежных граней, угол между которыми меньше или больше min_angle .

• 3)    Пересчитываем координаты этих точек так, чтобы угол смежных граней стал равен 180 градусам:

  • 3.1)    Координаты данной точки M рассчитываются как координаты проекции этой точки на плоскость, содержащую все вершины смежных граней. Другими словами, находим точку пересечения прямой и плоскости в пространстве.

  • 3.2)    Присваиваем точке M координаты ее проекции.

• 4)    Повторяем пункты 2 и 3, пока не останется углов меньших, чем min_angle , либо пока количество итераций не станет равно iterations.

• 5)    Возвращаем сглаженную фигуру в формате .stl.

Результаты выполнения функции сглаживания и трансляции представлены на рис. 6, 7.

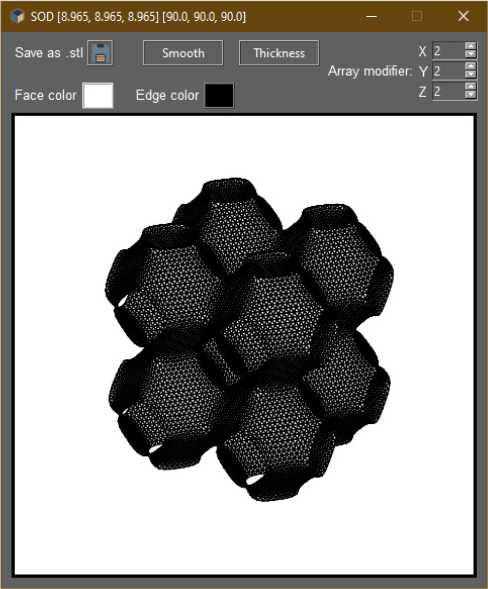
Рис. 7. Сглаженная и транслированная трехпериодическая поверхность, полученная из каркаса SOD

Fig. 7. Smoothed and translated three-period surface obtained from the SOD framework

Логику данного алгоритма можно сформулировать следующим образом: чем ближе двугранный между соседними гранями стремится к развернутому углу, тем меньше средняя кривизна в общих точках этих граней.

Описанный выше алгоритм сглаживания по средней кривизне уменьшает значение средней кривизны в каждой точке поверхности. Чтобы показать это, был проведен расчет с разным значением n алгоритма сглаживания. Результаты представлены на рис. 8, 9.

Из графиков видно, что ближайшее значение средней кривизны в каждой точке к нулю получается при использовании параметра n = 3. Следовательно, можно модифицировать алгоритм следующим образом:

Образец задания процедуры сглаживания: _smooth (mesh, min_angle, iterations) , где mesh – несглаженный каркас; min_angle – минимальный желательный угол между смежными гранями каркаса, при идеальном варианте равен 180 градусам; iterations – количество повторений операций смещения точек смежных граней с углом неравным min_angle .

Обновленный алгоритм сглаживания заключается в следующем.

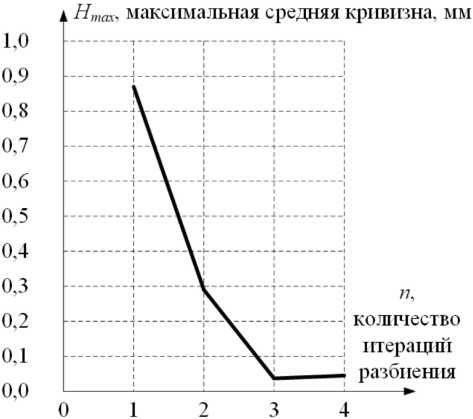
Рис. 8. График расчета максимальной средней кривизны для поверхности, полученной из каркаса SOD

Fig. 8. Graph of the calculation of the maximum average curvature for the surface obtained from the SOD wireframe

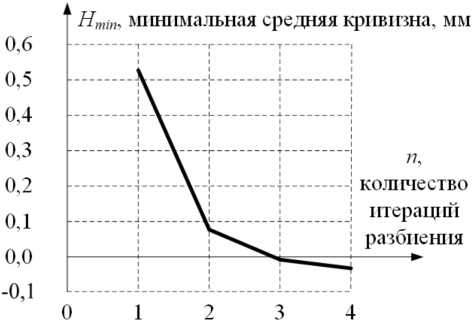
Рис. 9. График расчета минимальной средней кривизны для поверхности, полученной из каркаса SOD

Fig. 9. Graph of the calculation of the minimum average curvature for the surface obtained from the SOD wireframe

• 1)    Рассчитываем A H = H   - H   до сглажи-

• 1 max min

вания, присваиваем n = 2.

• 2)    Разбиваем фигуру на большее количество треугольников в n раз.

• 3)    Ищем точки смежных граней, угол между которыми меньше или больше min_angle.

• 4)    Пересчитываем координаты этих точек так, чтобы угол смежных граней стал равен 180 градусам.

  • 4.1)    Координаты данной точки M рассчитываются как координаты проекции этой точки на плоскость, содержащую все вершины смежных граней. Другими словами, находим точку пересечения прямой и плоскости в пространстве.

  • 4.2)    Присваиваем точке M координаты ее проекции.

    

    Рис. 10. Напечатанная сглаженная модель пористого материала, полученная из каркаса SOD

    Fig. 10. Printed smoothed porous material model obtained from the SOD framework

    
    
    

    Рис. 11. Напечатанная несглаженная модель пористого материала, полученная из каркаса SOD

    Fig. 11. Printed non-smoothed porous material model obtained from the SOD framework

    
    

• 5)    Повторяем пункты 2 и 3 пока не останется углов меньших, чем min_angle, либо пока количество итераций не станет равно iterations.

• 6)    Рассчитываем AH₀ = H„„„ -H   после сгла-

• 2 max min
4.    3D-печать

живания. Если A H 2 < A H 1 то n = n + 1, A H 1 = A H 2 , и идем на пункт 3. Если A H 2 > A H 1 , то возвращаем сглаженную фигуру в формате .stl, полученную на предыдущем шаге.

Для 3D-печати модель должна обладать некоторой толщиной. Для придания соответствующей модели необходимой толщины был написан алгоритм, образец задания процедуры которого: solid (model, thickness), где model – модель, не имеющая толщины; thickness – толщина в условных единицах.

Алгоритм наращивания толщины заключается в следующем.

• 1)    Находим граничные точки модели, копируем их индексы и координаты в отдельный массив данных – copy .

• 2)    У всех вершин из copy рассчитывается нормальный вектор, и координаты вершин сдвигаются на расстояние thickness вдоль нормального вектора.

• 3)    Из полученных точек и их оригиналов, зная их индексы, создаем новые фасеты по правилу правой руки, которые будут являться ободом модели для печати.

• 4)    Аналогично 2 копируем и передвигаем оставшиеся вершины модели и аналогично 3 восстанавливаем фасеты на этих вершинах.

• 5)    Возвращаем фигуру с толщиной thickness в формате .stl.

Полученная модель (сглаженная и несглажен-ная) была распечатана на 3D-принтере Prusa i3 из PLA пластика, рис. 10 и 11.

Заключение

Полученные результаты позволят моделировать новые пористые и конструкционные материалы, прогнозировать их механические и адсорбционные свойства, необходимые для использования в нефтехимической промышленности, на предприятиях аэрокосмической, автомобильной и медицинской отрасли.

Работоспособность созданной системы моделирования пористых материалов на основе генерации пористых каркасов и получения на их основе трехпериодических поверхностей подтверждена путем генерации 103 примеров пористых каркасов, соответствующих им трехпериодических поверхностей с семействами непересекающихся пор и построения на их основе пористых материалов.

В следующих работах планируется сравнить разработанный алгоритм по быстродействию с алгоритмом приближенного отыскания гармонической функции методом конечных элементов с помощью решения уравнения Лапласа после триангуляции плоской области, получающейся проекцией кольца на некоторую плоскость.

Авторы выражают свою благодарность за ценные замечания и помощь в работе профессору Блатову В.А., профессору Блатову И.А. и Барабанову В.С. Работа выполнена при финансовой поддержке Минобрнауки РФ в рамках государственного задания № 0778-2020-0005.