Разработка программы для численного газодинамического моделирования на основе лагранжево-эйлеровой схемы LES - ASG

DOI:

В данной работе проведено сравнение двух типов решения уравнения переноса с неоднородным распределением скорости, а именно LES (лагранжево-эйлерова схема) и MUSCL (Monotonic Upstream-Centered Scheme). По результатам сравнения можно определить эффективность схем, а также точность по отношению к вычислительным затратам для схем равного порядка точности. Все полученные данные будут способствовать дальнейшей реализации схемы LES — ASG уравнений газодинамики.

• 1.    Численные схемы

Разработка новых и модификация уже существующих численных методов для повышения их эффективности всегда были актуальными задачами вычислительной математики. Это связано как с практической необходимостью нахождения решений новых сложных задач, так и самой логикой развития численных методов как раздела прикладной математики.

Для построения численного алгоритма необходимо прежде всего четко поставить математическую задачу, эквивалентную данной физической задаче. Кроме того, алгоритм, позволяющий корректно производить вычисления, должен удовлетворять ряду требований, чего не всегда просто добиться в каждой конкретной ситуации.

Известно, что решения различных задач математической физики, которые описываются гиперболическими системами уравнений, могут быть гладкими в одних областях и разрывными в других [1; 5; 6; 8; 9]. Разрывные решения могут при этом возникать из гладких начальных данных. Такие свойства решений налагают на алгоритмы численного решения достаточно жесткие требования. С одной стороны, численный метод должен уметь сохранять свойство монотонности в тех областях, где искомые решения имеют большие перепады значений. С другой стороны, тот же метод должен обладать высоким порядком точности в тех областях, где решение является гладким.

• 1.1.    Схема MUSCL

Данная схема относится к методу конечных объемов, обеспечивает высокую точность решения. Идея состоит в том, чтобы заменить кусочно-постоянную аппроксимацию на реконструкцию ячеек и получить их промежуточные состояния на каждом временном шаге. Для каждой ячейки ограничен угол наклона, реконструкция левой и правой ячейки производится непосредственно через вычисление потоков на границах ячеек [3; 11].

• 1.2.    Схема LES

Численные схемы, основанные на лагранжевом или эйлеровом подходах, обладают как преимуществами, так и недостатками. Комбинирование лагранжева и эйлерова подходов в рамках одного алгоритма позволяет объединить преимущества обоих методов. Для численного решения можно применить схему «предиктор — корректор». LES является обобщением новой численной схемы cSPH — TVD (combined Smoothed Particle Hydrodynamics — Total Variation Diminishing) [4; 7; 10; 12; 13]. Схема LES строится для уравнения переноса, не только для гидродинамического моделирования, но и прекрасно подходит для задач по переносу загрязненных примесей в приземном слое атмосферы [2].

• 1.3.    Кусочно-постоянная реконструкция

Рассмотрим одномерное уравнение переноса с неоднородным распределением скорости:

^ +     =0,    В - В(t) -const.

at ox

Применив схему MUSCL к уравнению (1), получим

Q " ⁺ -(1 - A i (i))Q " + A 2 (i)Q '- ₁ ,                       (2)

где

A i (i)- 0 +1 / 2 (1 -        - ',

A s et) - G - 1 / 2 (1 - ^{C i}-^{1/2 - С ,-3/2} ) .

Следует учитывать условия устойчивости

С , -     ,      С , <  1.

h

Для реализации схемы LES уравнение (1) будет иметь вид o„+1_ .     B1№\

Q, Д1-     QQ, + где

В1(г) = С,+1/2,(6)

^B 2 ^{( t}) ^{- С} , - 1/2 .

Погрешность для обеих схем рассчитываем через соотношение (7)

N е - ^ Е |Q, - Q'|,    С, < 1.(7)

• 1.4.    Кусочно-линейная реконструкция

• 2.    Проведение вычислительных экспериментов

  Проведем сравнение численных схем MUSCL и LES для кусочно-линейной и кусочно-постоянной реконструкции для решения уравнения переноса с неоднородным распределением скорости. Следует обратить внимание, что обе схемы совпадают при U = = const, а также схемы хороши для реализации переноса гладких профилей, поэтому рассмотрим, как будет вести себя профиль, представленный на рисунках 1 и 2.

  

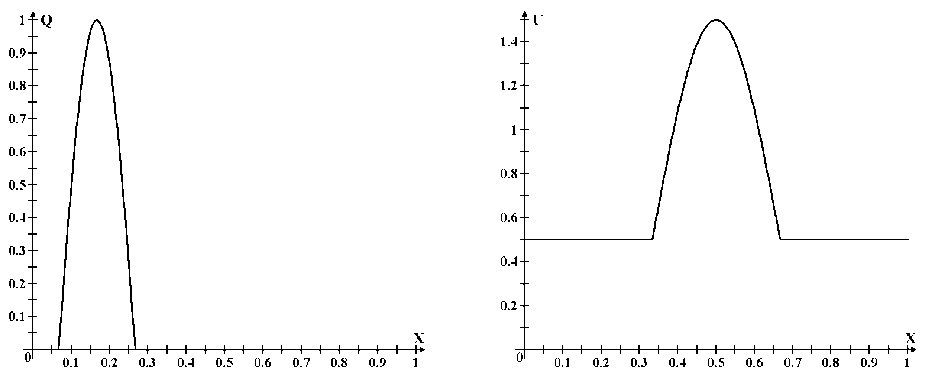
  Рис. 1. Исходный профиль Рис. 2. Профиль скорости

  
  

Применив схему MUSCL к уравнению (1), получим

Q"+1 - (1 - Ai(.))Q” + A2(.)Q'-i - Аз(г)А”h + A4(.)A'-ih,(8)

где B 1 ,B ₂ ,B 3 и B ₄ рассчитываем через соотношение (9)

A i (t)-C . +i / 2 (1 - ^{С ,+1/2 -С ,-1/2} ) ,

A s (t) - С ,- 1 / 2 (1 - ^С '^-1/2 - ^С '^-3/2 ) ,

Д       _Г (    ^С ' +1 / 2 + ^С '- 1 / 2 А

A3(t) - С'+1/2 I 1^) ,

Д       _п           ^С '- 1 / 2 + ^С '- 3 / 2А

^A 4 ^{( t ) - С} '- 1 / 2 11^I .

Как и в кусочно-постоянной реконструкции, следует учитывать условия устойчивости (4).

Для реализации схемы LES применим шаг «предиктор — корректор» к уравнению (1) и в результате получим

Q " ⁺¹ = (1 -        Q" + ^Q ?- , - Вз(ОД t + B 4 ( . ) A ' - i |,       (10)

⁵ +            ⁵ +-1                   ^{2              2}

где В 1 , В ₂ , В ₃ , В 4 , 5 + и 5 +1 рассчитываем через соотношения (11) и (12)

В 1 (г)= С _{г +}1 / 2 ,

В 2 (г) = С _г- 1 _/2 ,

^В 3 ⁽ ^ = ^С г+1/2 ⁽¹ - ^С г ),

^В 4 ⁽ г) = ^С г - 1/2 ^{(1 — С} г- 1 ⁾-

^{5 +} = ¹ + ^С г+1/2 ^{— С} г , ⁵ +-1 = ¹ + ^С г- 1 / 2 ^{— С} г- 1 .

Проведем тестовые расчеты и получим решения на сетках с частотой дискретной пространственной дискретизации N : 300, 600, 1 200, 2 400, 4 800, 9 600. Будем использовать ограничитель minmod. Количество итераций для N = 300 будет 970, а для каждого последующего N количество итераций увеличивается в два раза, для удовлетворения условия (4).

/ ^U i+1 - U i ^U i - ^U i - 1

\ h ’ h

= -(szyn(a) + S2gn(b))mm( | a | , | b | ).

L(a, b)

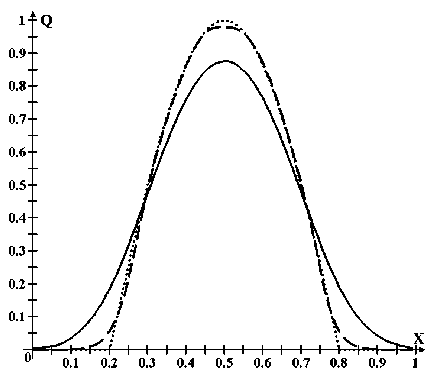
Рис. 3. Конечные профили для схемы LES при N = 300 , где: сплошная линия — это кусочно-постоянная реконструкция; прерывистая линия — это кусочно-линейная реконструкция; пунктирная линия — это исходный профиль

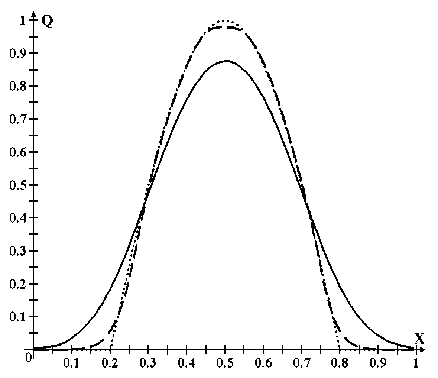
Рис. 4. Конечные профили для схемы MUSCL при N = 300 , где: сплошная линия — это кусочно-постоянная реконструкция; прерывистая линия — это кусочно-линейная реконструкция; пунктирная линия — это исходный профиль

Обратим внимание на то, что обе схемы (рис. 3 и 4) почти полностью совпадают в конечных профилях. Более подробные результаты испытаний представлены на рисунках 5–8, а также в таблице 1.

Таблица 1

Результаты тестов, погрешность вычислений

N	Кусочно-постоянная реконструкция		Кусочно-линейная реконструкция
	MUSCL	LES	MUSCL	LES
300	7, 5455 х 10 - 2	7, 5451 х 10 - 2	2, 0163 х 10 - 2	1,0191 х 10 - 2
600	4,2171 х 10 - 2	4, 2169 х 10 - 2	5, 7162 х 10 - 3	5, 7275 х 10 - 3
1 200	2,2633 х 10 - 2	2, 2633 х 10 - 2	2,6335 х 10 - 3	2, 6309 х 10 - 3
2 400	1,1818 х 10 - 2	1,1818 х 10 - 2	1,2402 х 10 - 3	1, 2411 х 10 - 3
4800	6, 0794 х 10 - 3	6, 0794 х 10 - 3	5,9244 х 10 - 4	5, 9223 х 10 - 4
9600	3, 0903 х 10 - 3	3, 0903 х 10 - 3	2,7158 х 10 - 4	2, 7163 х 10 - 4

Составим формулу, по которой будем сравнивать кусочно-линейную схему MUSCL с LES.

N

F(х) = 1од_ш ^Q i — Q * ,                        (14)

i =0

где Q _i — решение по MUSCL, а Q* — решение по LES.

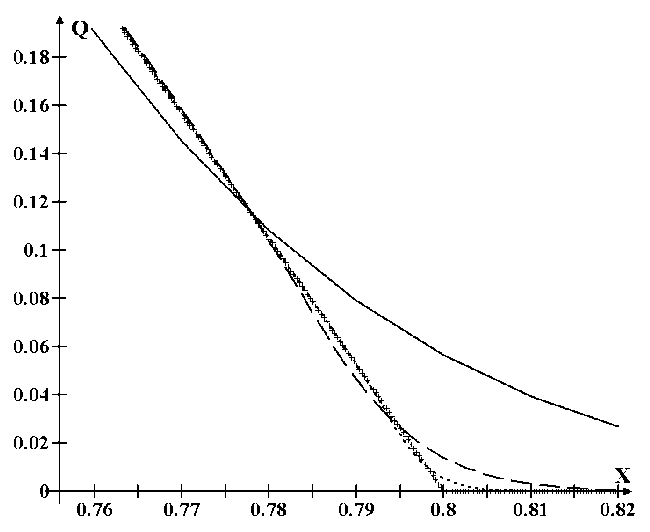
Рис. 5. Вырезка из конечного профиля схемы LES с кусочно-линейной реконструкцией на сетках N = 300 (сплошная линия), N = 2 400 (прерывистая линия), N = 9 600 (пунктирная линия), исходный профиль (плюс)

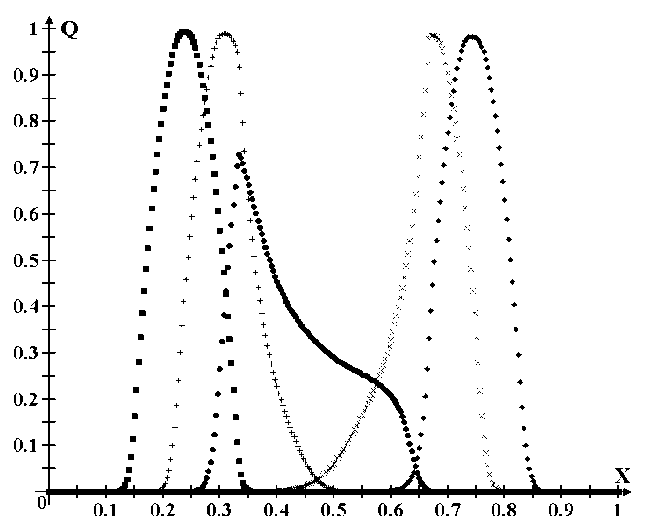
Рис. 6. Профиль схемы LES с кусочно-линейной реконструкцией в моменты итераций

150 (квадрат), 300 (плюс), 450 (круг), 700 (крест), 850 (ромб), для N = 300

При проведении тестовых расчетов мы получили данные, на основе которых можем полагать, что численные схемы MUSCL и LES одинаково хорошо применимы для моделирования уравнений переноса.

По итогам проведенной работы мы удостоверились в правильности выбора схемы LES для последующей разработки программы для численного газодинамического моделирования на основе схемы LES — ASG.

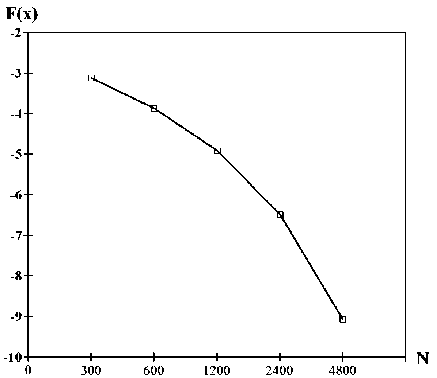
Рис. 7. Отличие кусочно-линейной схемы MUSCL от LES по формуле (14)

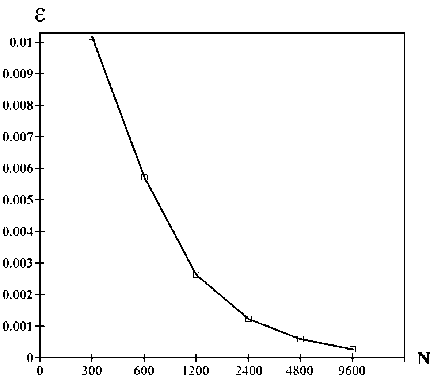
Рис. 8. Погрешность вычислений кусочно-линейной схемы LES