Разработка схемы численного расчета параметров нелинейных электрофизических процессов методом минимизации функции сравнения

В последнее десятилетие интенсивные темпы развития вычислительной, цифровой техники и программио-аппаратиого обеспечения способствовали существенному усовершенствованию чис-

• ¹    E-mail: kalytka@mail.ru

лепных методов решения уравнений математической и теоретической физики, методов статистической обработки результатов лабораторных экспериментов, методов сравнительного численного анализа, степени точности теории по отношению к эксперименту и методов компьютерного прогнозирования результатов экспериментов [1-6].

Эффективным, с точки зрения оптимизации вычислительного процесса, инструментом сопоставления результатов экспериментальных и теоретических исследований является метод минимизации функции сравнения (МФС-метод), применяемый при математическом моделировании различных физических процессов, протекающих в неоднородных физических системах, эволюционирующих во времени под действием различных полевых факторов и температуры. МФС-метод получил достаточно широкое распространение в различных областях науки и техники и остается актуальным при численной оптимизации параметров работы технологических схем различных информационно-коммуникационных систем и промышленных установок, что подтверждается рядом работ последнего времени [7-12].

В [1] рассмотрен метод минимизации времени простоя пользовательских процессов при их миграции в «облачном хостинге». Реализация данного метода, осуществляется путем: прогнозирования времени остановки процессов; сокращения объема, оперативной памяти, затрачиваемой при миграции [1].

В [2] исследован вопрос по использованию метода, модифицированных функций Лагранжа. (МФЛ) при численной оптимизации процессов, с учетом голономных связей в механических системах. Развитие методов учета, дополнительных геометрических и кинематических связей, позволяет существенно расширить методы численной оптимизации процессов в механических системах со структурой типа, «дерева» па. структуры с кинематическими связями [2]. Метод МФЛ, применяемый при компьютерной оптимизации [3-6] технологий изготовления различных деталей и при сборке машин и механизмов, находит применение в различных областях современной электротехнической промышленности и в машиностроении [7-9].

В [10] выполнена, модификация методов расчета, поля скоростей потока, па. примере решения задач, связанных с кавитацией. В ходе исследований усовершенствованы существующие и разработаны новые методы численного расчета, и обнаружения пузырей воздуха, в жидкостях по изображениям [11].

Разработанные алгоритмы расчета, параметров потока. [11, 12] актуальны при численной оптимизации технологических схем гидроустановок и электроустановок, при проектировании в области турбостроения, кораблестроения, ракетостроения и др.

1.    Постановка задачи исследования

Центральная идея данной работы состоит в изложении теоретических основ обобщенной математической модели, позволяющей, па. основе алгоритма, компьютерной программы (или комплекта. программ) проводить эффективные, с высокой степенью точности, численные расчеты параметров эволюционирующих во времени нелинейных подсистем, входящих в систему, находящуюся под действием различных силовых полей (внешних, локальных) и тепловых потоков. Такого типа, модельные системы, по свойствам и структуре, приближены к функциональным элементам, входящим в состав технологических схем различных силовых установок и систем, работающих в условиях реального производства.

Цель работы состоит в описании обобщенной схемы математического моделирования и численного расчета, параметров релаксационных физических процессов (поляризация, проводимость), протекающих в разнородных функциональных элементах (ионные проводники, тонкопленочные изоляторы, регуляторы параметров излучения, элементы памяти ЭВМ, топливные элементы водородной энергетики) электротехнических схем оборудования, работающего при изменяющихся условиях (переменные силовые поля, температура).

Методология исследования строится на. МФС-методе, устанавливающем, в комплексе с чис- лепными методами исследования свойств функций многих переменных [13], оптимальное математическое соответствие между теоретическими (расчетными) и измеренными в эксперименте значениями характеристических параметров физической модели.

В данной статье, в качестве предмета исследования выступает частный случай обобщенной математической модели поляризационных процессов релаксационного типа. [14], протекающих (в достаточно широком диапазоне полей и температур) в слоистых диэлектрических структурах ^объект исследования), на. примере кристаллов с водородными связями (КВС), классифицируемых, по электрофизическим свойствам, как протонные полупроводники и диэлектрики (ППД) [14-18]. В качестве параметров (характеристик) релаксационных процессов в ППД принимаются [15, 16]: U_o - энергия активации (высота, потенциального барьера) наиболее подвижных (в данной физической модели) частиц (протонов), двигающихся по водородным связям (за. счет термической активации, или туннелирования); vo - линейная частота собственных колебаний релаксаторов (протонов) в потенциальной яме; no - равновесная коицентрация протонов; So - ширина потенциального барьера.

Теоретические исследования нелинейных эффектов при квантовой поляризации в ППД в области низких (70-100 К) и сверхнизких (1-10 К) температур выполнены в [15, 16]. Математическая модель нелинейной объемно-зарядовой поляризации в области высоких (250-550 К) и сверхвысоких (550-1500 К) температур строится в [17, 18]. При этом в [15-18], теоретические основы методов численного исследования нелинейных поляризационных процессов не рассматриваются.

В [19-21] алгоритм численного расчета параметров Uo, vo, no, So, на основе МФС-метода, не раскрывается детально.

2.    Построение и анализ функции сравнения теории и эксперимента

Физико-математическая модель протонно-релаксационной поляризации в материалах класса. ППД (в частности, КВС) [15-19] позволяет строить теоретические температурные спектры плотности токов термостимулированной деполяризации (ТСТД) - Jtcdp (Т ) [14] и частотнотемпературные спектры тангенса угла диэлектрических потерь tg 5 (ш; Т ) [21], обусловленные вкладом только одного типа, релаксаторов - протонов [14]. Методы кинетической теории [14-18, 20, 21] эффективны, с точки зрения точности численных расчетов спектров Jtcdp (Т ) и tg 5 (ш; Т ), только в окрестности (па. множестве точек меры континуума) экспериментально наблюдаемого максимума.

Положение теоретического максимума функции Jtcdp (Т ) определяется точкой (Т_тах; Jtcdp, max) ^в пространство характеристик моиорслаксаипоипого процесса, {^ф; Т_тах^. где ^ф = {U_o,th;v_o,th;n_o,th; 5_o,_th} ~ многомерный радиус-вектор, построенный на множестве теоретических значений параметров ^ф = {U_o; v_o;n_o; 5_o} [21]. Положение теоретического максимума функции tg 5(^^ро1^ (Т ), при постоя!шой частоте ш_роц определяется точкой ^Т_max;tg S^max⁰¹)^, в пространстве характеристик {^ф;Т_тах^. Аналогично, положение максимума функции tg 5^(Тро1 ) (ш), при постоянной температуре поляризации Т_роц определяется точкой ^ш_max;tg 5mmОХ” )^ в пространство {^ф; ш_Хх |

Движение изображающих точек {^ф;Т_тах^, {^ф; ш_тах^ в пространстве характеристик процесса ^ф приводит к изменению теоретического значения времени релаксации, а значит и к смещению точек максимумов (Ттах; tg 5(паХ^о1)) , ^Штах; tg 5ma^px^l )) , (Ттах; Jtcdp, max ) ПО осям абсцисс, а также к изменению амплитуд максимумов [21].

Достаточно высокая степень точности численного расчета, точек максимумов функций Jtcdp (Т), tg 5(1ар°г) (Т), tg 5mmОХ”1) (ш), в сравнении с результатами [20, 21] будет обеспечиваться численной оптимизацией функциональных зависимостей компонент радиус-вектора f от значения Tmax и wmax. С этой целью вводится функция сравнения теории и эксперимента [14]

ф (^f) = \e_th (f) - 0exp]2,

Здесь 0th

(f)

абсцисса, соответствующая положению теоретического максимума, на. графике,

которая устанавливается расчетным путем; 0exp — абсцисса, соответствующая положению экспе

риментального максимума, на. графике, который строится по результатам прецизионных измере ний.

Согласно (1) функция сравнения Ф

(о

не может быть отрицательна.

Абсцисса 0_exp моделируется либо в качестве температуры материала T_max,_exp

либо в каче

стве частоты возмущающего переменного внешнего поля wmax,exp, соответствующей измеренному в эксперименте мопорелаксациошюму максимуму физической характеристики процесса, (плотности тока, поляризации).

Абсцисса 0th (f)

устанавливается в результате исследования на. максимум математического выражения, описывающего теоретический монорелаксационный спектр. Данное выражение явля ется результатом аналитического решения системы дифференциальных уравнений [15-19, 21] и в, общем случае, исследуется на экстремум как функция от переменных (f; т( или (ф w)- и, в конечном счете, сводится к установлению функциональных зависимостей вида:

Л"»'1 (fmax)

Л(Т»”г) (fmax)

= T^V max,th

^"^(т ;Д

tg    )И)

wmax,th

( ^0,th,max; ^0,th,max; ^0,th,max; ^0,th,max) ;

⁽Uo,th,max^; ^0,th,max; ^0,th,max^; ^0,th,max) ^;

O (fmax)

— ^T_max th           ⁽U"o,th,max; ^0,th,max^; ^0,th,max^; ^0,th,max) -

(2-1)

(2-2)

(2.3)

В (2.1)42.3) Л^"»^ (fmax) - вычисленное в пространстве критических значений параметров (max = {Uo,th,maxV^O,th,max;no,th,max; ^0,th,max} ЩЖ ПОСТОЯННО!I чаСТОТС ПОЛЯ wpol ЗИачСПИС ТСМ- пературы h

теоретического максимума функции Ф1 (т; ^f) = tg 5^(_h^P°¹^ (т; ^f);

Л(т»°г) (fmax) — вычисленное в пространстве критических значений fmax при постоянной темпе-

[tg ратуре ТрО1 значение частоты wmax th

теоретического максимума функции Ф2 (w; f) =

= tg ф(»^oi) (w; f): O (f_max) - вычисленное в пространстве fm_ax значение температуры теоретического максимума функции Ф3 (т; f) = JTCDP,th (т; f).

Громоздкость функций Ф1 (т; f), Ф₂ (w; f), Ф3 (т; f) не даёт возможности детально исследовать аналитические выражения Л^(ш»=1) (fmax), Л^(т»О (fmax), O (fmax) - Тогда, пренебрегая температурной (или частотной) зависимостью характеристик ( в окрестности точки экспериментального максимума. [21] упрощаем процедуру минимизации функции сравнения (1). Из системы уравнений дФ1(т ;f)      8Ф2(_Ш;Д       ЭФз(т ;f)               O-rl - С 1 - С         ,

—8^г^ = °- —84"^ = °- — 8^^" = °-^г'^ = р^г;^тг ^Sj = с; ^wV ^Sk = 1 ^fk; ^тг ^ПС1^{,СХОД1П1 к} выражениям ^1» (Tmax,th; fmax) = °- ^2j (wmax,th; fmax) = °- ^3k (Tmax,th; fmax) = °- НОЗВОЛЯТОШИМ построить функции, выражающие каждый из параметров из множества, критических значений

f

f

f_max. вклточая T ii w. через все остальные параметры множества. f_max (вклточая Т и w) в точках теоретических максимумов соответствующих функций Ф1 (т; f), Ф₂ (w; f). Ф3 (т; f). Тогда.

_T [M^T 01

"*~ m о v + ri

.911 (max) ,

K-Y  n (f )  THT=01

^wmax,th   = 922 Tmax,th

933 ^(max) .

Выражения (3) позволяют перейти к расчету функций сравнения

Ф 1 (( max) =

т №=0] т

Г. х ^{( ш}р°¹ tg ⁵exp тк „~ max , exp

}(Тф,)]"

, Ф 2 ((max) =

_yW max ,t^

[     ^{( т}ро1

tg 5exp wmax,exp

W)]"

,

* 3 (( max ) = [rm^^{1 5}» -     .p          ² .                    ,4,

В (4) компоненты вектора (0 = {U₀,_exp; v₀,_exp; n₀,_exp; 5₀,_exp} вычисляются в окрестности соответствующих экспериментально измеренных максимумов тангенса угла потерь tg ^Lp”⁰¹) (т; (0), (^T ”oi )

tgoexp    w; (o и плотности термостимулированного тока JTCDP,exp М ; (o I, с помощью методов, описанных в [14].

Процедура, минимизации функций (4), с помощью формул д^2 ((max)

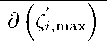
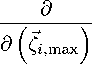
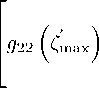
[ tg 5^ (_Ш;ф)] ^w max , exp

= 2

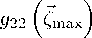
^w max , exp

[^tg S exp \“Ф⁰)]     Эд22 (( max )

•

•

d (⁽, max)

0,

(5.2)

dФ 3 (( max) d (( max )

д

d (( max)

833 (( max )

rp [ J tcdp ,exp( ^T Фо)] 1 2 ^т max , exp

2 933 (( max)

rp [^{i ,} TCDP, exp ^т max , exp

(T Фо)]"|   ⁹⁸³³ ((max)

•

d (( max)

0,

(5.3)

позволяет записать минимизированные значения параметров (3), каждому ся в соответствие некоторые множества l,m,n векторов ((_max;opt,z), ((_{max;op f}

из которых ставят-

f

), где

f

BeKTOp ⁽ max; opt, 1 — ^{U 0 ,t^, max; opt, 1 ^; ^ 0 ,t^, max; opt, 1 ^; ^ 0 ,t^, max; opt, 1 ^{; S} 0 ,t^, max; opt, 1 } Отвечает ТОЧКаМ ЭКСПе-

[tgi-h^T ;5o)]    [tg ^(xT’ риментальных максимумов Tmax,exp       J , wmax,exp

^Фо)]

_m [- ? TCDP, exp ( ^T ; <□)]

- rmax,exp            . а. все осталь-

д Ф1 ((max) д (fi,max) д              (f )       [tg 5exxPo1)(T;ф)] 2 —   ( .    ) 911 ^(maxJ   Tmax,exp            — \      tg5expP ^(tФо)     д9и ((max) = 2 911 ((max)   Tmax,exp            •    ((    ) = 0,            (5-1) ные вектора, отвечают всем возможным, распределенным вблизи экспериментальных значе т [Ф1(т;0] (max,th);opt,l

911 ^⁽ max; opt,l^ -

ний мипимизироваппым теоретическим значениям параметров

^fcx^opt,™ = 922 ((max;opt,m), T(m£’tK)?opt^ = 933 ((max;opt,n) • Эти Значения ВЫЧИСЛЯЮТСЯ ИЗ д911(

равнении "^(^-^mxy- = ⁰ "^(^-mxp- = ⁰-^^max^" = ⁰

По результатам численных исследований, функции сравнения (4) имеют в пространстве ха- рактеристик (max сложный рельеф. Некоторые характеристики меняются в небольших пределах, так например энергия активации выбирается из интервала. (0,05; 0,7) эВ, в то время как равновесная концентрация релаксаторов при движении теоретического максимума, по оси температур может изменяться на. несколько порядков. Это приводит к тому, что рельефом функции сравнения оказывается многомерный сложный извилистый и очень узкий овраг, содержащий большое количество минимумов. В вычислительной математике разработаны простые в техническом отношении методы, позволяющие пройти вдоль оврага, и выйти в котловину минимума, однако эти методы расчёта, капризны, и алгоритм прохождения по оврагу содержит ряд не формализуемых поправок, которые должны вноситься в программу прямо по ходу вычислений [13, 22, 23]. Скорость движения вдоль оврага, очень небольшая. Результативность поиска, минимума, функции сравнения при таком ее рельефе очень сильно зависит от того, насколько удачно удалось подобрать пулевое приближение для характеристик. Удобным является изменение масштаба, с помощью двойного логарифмирования по разным основаниям. Удачный выбор оснований логарифмов сокращает время вычислений. На выбор оснований влияет подбор пулевого приближения. Большую помощь оказывает точный эксперимент.

Приближенный способ минимизации функций сравнения (4) вдоль одного из направлений из множества Сш_ах, включая Т, или ш, осуществлялся методом парабол, при котором соответствующие приближения I + 1,m + 1,п + 1 связаны с приближениями 1,т,п одномерных г-ых минимумов

А

^С(г,шах);( opt,l + 1)

А

С(г,шax);(opt,l)

Хг;1

А (^А(г,шах);1 ^{+ Х}щ) ^— ^1 (^А(г,шах);1 ^{— Х}г;1^

² ^1 (С(г,шах);1 ⁺Хц^ - 2Ф1 (фшах);^ ⁺ ^1 (С(г,шах);1 ^—Х^

(6.1)

^С(г,шax);(opt,m+1)

^С(г,шax);(opt,т)

Хг;т

^С(г,шах);т ^{+ Х}г;т) — А (А(г,шах);т

Аг;т 1

С(г,шах);т ^{+ Х}г;т) — 2Ф2 (С(г,шах);т) + а (с(г,шах);т

^{— Х}г;т^

(6.2)

л»

л»

^Хг;п

^С(г,шах);п ^{+ Х}г;п^   ^3

г,шах);п

С(г,шах);п ^{+ Х}г;п^ ^{— 2}^3

— \A»J

г,шах);п^ ⁺ *3 ^С(г,шах);п

^— Хг;п)

(6.3)

В (6.1)-(6.3) координат, вдоль

С(г,шах);1, С(г,шах);т, С(г,шах);п - Соответствующие фуНКЦИЯМ Сравнения (4) ОСИ которых производится очередной спуск. Вспомогательный шаг, в этих случаях,

Хг;1 = Хит. = ХЦп = 0, 0001. Такая аппроксимация эквивалентна замене сечений рельефов функций сравнения интерполяционными параболами, построенными по трём точкам фг,шах);а —Хца А(г,шах);а А(г,шах);8 + Хг;з, Г Де S = {Z, т, п}.

3.    Особенности программы минимизации функции сравнения

В программе минимизации функции сравнения (1) предусматривается возможность формирования пространства, характеристик. После запуска, программы в диалоговом режиме задаются все необходимые для расчёта, параметры. Задаются также и критерии, позволяющие выяснить, перебором каких именно параметров следует минимизировать функцию сравнения. Эти критерии могут принимать два. значения - нуль и единица. Так, например, если критерий необходимости минимизации функции сравнения путём перебора, значений энергии активации равен единице, то ЭВМ включает энергию активации в список параметров сравнения. Задание числовых значений всех критериев необходимости минимизации формирует пространство характеристик. В процессе задания пулевого приближения значения характеристик предполагается деформация рельефа, функции сравнения, который поначалу представляет собой узкий извилистый овраг. С этой целью путём двойного логарифмирования характеристик формируется область котловинного типа, размеры которой сравнимы с единицей.

Программа, перегружена, операторами условия, что связано с необходимостью различия значимых и не значимых параметров расчёта, в процедуре перебора.

После того, как сформировано пространство характеристик, выбирается область, в которой будет минимизироваться функция сравнения, задается пулевое приближение координат изображающей точки и выполняется процедура, спуска, по координатам. При реализации спуска, существенную роль играет порядок следования осей координат. Наибольший вклад в смещение теоретическо го мопорелаксациоппого максимума, вносит изменение экспоиеициальио входящих характеристик (энергия активации, ширина, потенциального барьера). Именно по этим направлениям спуск производится в первую очередь. Каждый цикл спусков завершается сверкой полученного значения функции сравнения с минимально допустимым значением. Поиск минимума, при изменении одной координаты в пространстве характеристик и расчёт значений функции сравнения выносится в блок подпрограмм, располагающихся после головной программы.

Подпрограмма, построенная для численного расчета, по формулам (6.1)-(6.3), осуществляет поиск минимумов функций сравнения (4) при спуске по одной из координат. Итерационный процесс одномерного спуска, должен приводить к убыванию функций сравнения. В случае же увеличения значений функций сравнения управление передаётся подпрограмме, которая корректирует полученное в итерационном процессе значение изменяющейся координаты.

Назначение заключительной подпрограммы состоит в расчете значений функций Ф1 ^Т; () = = tg S^⁰') (т; ^f), Ф2 (w; ^f) = tg 5^°^l) (w; ^f), Ф3 (т; ) = J_TCDP,th (т; ) при текущих значениях параметров релаксационного процесса. Выполнение расчёта, зависит от возможности появления экспонент от больших чисел, что и определяет необходимость передачи управления подпрограммам, которые рассчитывают функции Ф1 ^Т; (^, Ф₂ (w;f). Ф3 (т; О в зависимости от определённых в различных вычислительных ситуаций [22, 23].

Заключение

В данной статье не ставилось целью разработать какие-либо принципиально новые методы математического моделирования и численного расчета, характеристических параметров систем. В этой области уже исследованы и используются па. практике достаточно эффективные методы [1-13], в том числе и МФС-метод.

Основная задача, данной работы состояла, в описании процедуры адаптации МФС-метода, его основных положений, применительно к численному расчету параметров разработанной в [1519, 21] физико-математической модели релаксационной поляризации в материалах класса. ППД. МФС-метод использован с целью повышения точности численных расчетов теоретических значений параметров ( = {U_0h; р^С Ti₀,th; S₀,_th}, путем ряда физических интерпретаций элементов функции сравнения (1), с учетом экспериментально и теоретически установленных закономерностей поведения частотных и температурных спектров функций Jtcdp (Т) [14] и tgS (w; Т) [21]. С этой целью построены более конкретизированные, по физическому смыслу, функции сравнения (4), исследовано их поведение на множестве характеристик (

Описаны особенности работы программы компьютерного расчета, где с помощью выражений (6.1)-(6.3) выявлены влияния формы рельефа поверхностей {(;Т^, |(; wj- на технологию поиска минимизированных согласно (5.1)—(5.3) числовых значений искомых параметров сравнения (2.1)(2-3).

Применения данного метода, численного расчета, дает хорошо согласующиеся с экспериментом результаты [21].

При этом, характеристики языка, программирования, практически не сказываются па. точности (порядка 0, 00001) результатов численного расчета параметров сравнения (2.1)—(2.3), по формулам описанной модели.

Таким образом, можно сделать следующие выводы:

• 1.    Сформулированы теоретические основы обобщенной математической модели, предназначенной для численного расчета, параметров релаксационных процессов при поляризации разнородных электротехнических материалов, в широком диапазоне варьирования полей и температур.

• 2.    В качестве примера, описан алгоритм минимизации функции сравнения (МФС-метод) результатов теории и эксперимента, при исследовании протонно-релаксационной поляризации в протонных полупроводниках и диэлектриках (ППД) и, на. этой основе, разработана, схема, численной минимизации параметров релаксационного процесса, (включая частоту переменного электрического поля и температуру).

• 3.    Выявлены особенности работы программы численного расчета, построенного па. алгоритме МФС-метода. применительно к расчету и анализу параметров спектров токов и диэлектрических потерь в КВС. Установлены возможности расширения диапазона, варьирования переменных параметров (частота, и амплитуда, поля; температура) процесса, при применении метода. МФ С для численного исследования более широкого круга, релаксационных процессов (магнитных, оптических, механических, тепловых и т.д.) в разнородных функциональных элементах технологических установок и систем.