Разработка системы реконструкции неоднородных тел элементарными объемами на примере керамики с дефектами микроструктуры

В настоящее время бронированная техника имеет, в основном, металлическую конструкцию (сталь, алюминиевые, титановые сплавы), что приводит к неоправданно высоким весовым показателям и необходимости иметь более мощные и тяжелые двигатели. Требования современного театра боевых действий заставляют разрабатывать легкие и скоростные транспортные средства с броней из керамики и полимерных волокнистых композитов [1, 2]. Однако количество варьируемых параметров при оптимизации защитной структуры исчисляется десятками [3–5], поэтому актуальной является разработка детализированных математических моделей деформирования и разрушения слоистых керамо-композитных структур для реализации конечно-элементных оптимизационных суперкомпьютерных вычислений.

Анализ современной литературы по механике разрушения неоднородных материалов показывает явную необходимость учета исходного состояния материала на микроуровне [1], т.е. учета дефектов структуры: распределения пор, включений и других несовершенств. Таким образом, многопараметричность моделей сплошной среды для керамики будет резко снижена за счет повышения «физичности и структурности» при отказе от гипотезы макросплошности. Перенос внимания на включение дефектов разного уровня в математические модели геометрии с упрощенным малопараметрическим описанием разрушения — мировой тренд численного анализа [6, 7].

Однако если для композитных материалов такой подход успешно применяется несколько лет [8–10], то в области моделирования керамических материалов есть всего несколько работ. Предлагаемые упрощенные аналитические модели [11] подходят только для первоначальных грубых оценок. Поэтому предлагается разработать систему реконструкции неоднородных тел элементарными объемами, где будет учтена микроструктура хрупкого керамического материала, полученные модели керамики будут использоваться при конечно-элементном моделировании процессов высокоскоростного удара на суперкомпьютере в пакете программ LS-DYNA.

Статья организована следующим образом. В разделе 1 приведена постановка задачи. В разделе 2 описывается реализация системы. В разделе 3 обсуждаются результаты исследований. В заключении суммируются основные результаты, полученные в данной работе.

• 1.    Постановка задачи

  • 1.1.    Функциональные требования к системе

Система должна предоставлять пользователю графический интерфейс со следующими возможностями:

• -    ввод имени входного текстового файла с граничными условиями (координаты точек);

• -    выбор количества измерений модели (2D или 3D);

• -    ввод размера конечного элемента (в двухмерном случае в качестве формы конечного элемента берется квадрат, в трехмерном — куб);

• -    ввод процентного соотношения нескольких материалов (например, 20 %; 15 %; 5 %; 60 %). При генерации сетки конечных элементов каждому конечному элементу в модели случайным образом присваивается один из нескольких заданных материалов, в результате на выходе получается модель с распределенными случайным образом свойствами материалов по объему.

Система должна обеспечивать создание k -файла (входного файла для расчета в пакете программ LS-DYNA) с узлами и конечными элементами тела в 2D или 3D постановке, реконструированного в соответствии с выбранными параметрами.

• 1.2.    Модульная структура системы

Система имеет модульную структуру:

• -    Модуль распределения свойств предназначен для распределения свойств материалов конечных элементов случайным образом по объему тела. Процентное соотношение материалов задано пользователем.

• -    Модуль анализа координат границ предназначен для обработки границ реконструируемого тела. Он выполняет следующие функции: считывание координат точек границы из входного файла; обработка границ; представление границ в системе.

• -    Модуль построения сетки предназначен для преобразования тела в набор конечных элементов. Он выполняет следующие функции: разбиение фигуры; анализ положения конечных элементов относительно границ фигуры.

• -    Модуль вывода предназначен для записи вычисленных координат узлов и конечных элементов в выходной k -файл. Данные в модуль вывода поступают из модуля построения сетки и модуля распределения свойств .

• 1.3.    Взаимодействие между модулями

• 2.    Реализация системы

На рис. 1 представлена схема взаимодействия между модулями системы. Стрелками обозначены потоки данных от одного модуля к другому. Основная программа предоставляет пользователю интерфейс для ввода параметров вычисления. Эти параметры обрабатываются и передаются в модуль распределения свойств и модуль анализа координат границ соответственно.

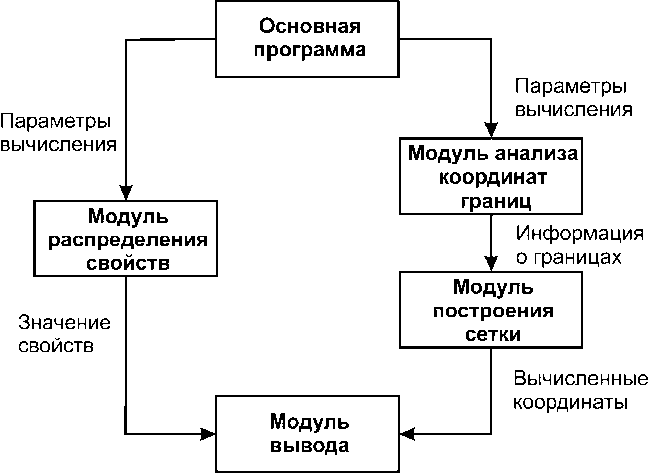
Рис. 1. Схема взаимодействия модулей системы

Пользовательский интерфейс (рис. 2) представляет собой форму ввода данных, необходимых для реконструкции тела. Для работы с приложением пользователю необходимо ввести имя входного файла, выбрать необходимое количество измерений, внести размер конечного элемента и процентное соотношение материалов. После этого нажать кнопку «Вычислить» и система построит модель на основе введенных параметров.

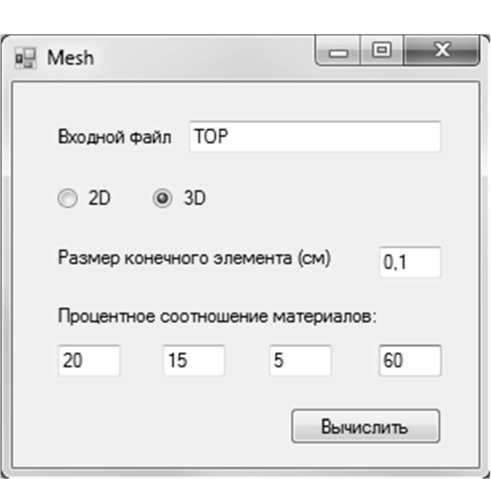
Рис. 2. Пользовательский интерфейс

Алгоритм работы системы включает в себя следующие шаги:

• 1.    Считывание координат границ из входного текстового файла. После считывания координаты записываются в vector (шаблон из стандартной библиотеки C++, реализующий динамический массив произвольного доступа), где с ними происходит дальнейшая обработка.

• 2.    Обработка границ и представление их в системе в виде конечных элементов.

• 3.    Вписывание тела в прямоугольник в двухмерном случае и в параллелепипед в трехмерном, на основе вычисленных крайних точек тела: минимумов и максимумов по каждой из осей.

• 4.    Заполнение полученного параллелепипеда конечными элементами.

• 5.    Определение принадлежности каждого конечного элемента реконструируемому телу. Для этого используется метод трассировки луча с учетом числа пересечений [12]. Из текущего конечного элемента выпускается луч по трем осям, по каждому подсчитывается число пересечений с границами, исходя из полученных данных, определяется положение конечного элемента относительно границ.

• 6.    Удаление конечных элементов, не вошедших в тело.

• 7.    Распределение свойств материалов конечных элементов.

• 8.    Запись вычисленных узлов и конечных элементов в k -файл.

• 3.    Результаты исследований

Для тестирования системы использовались различные выпуклые и невыпуклые двухмерные и трехмерные тела. На рис. 3 представлен один из тестов: разбиение тора на конечные элементы с процентным соотношением материалов 20 %, 15 %, 5 %, 60 %.

Рис. 3. Разбиение тора на конечные элементы с процентным соотношением материалов:

20 % (черный), 15 % (светло серый), 5 % (темно серый), 60 % (белый)

Заключение

Разработана система реконструкции неоднородных тел элементарными объемами на примере керамики с дефектами микроструктуры. В ходе работы были решены следующие задачи: спроектирована и реализована система реконструкции неоднородных тел элементарными объемами, проведено тестирование системы на различных выпуклых и невыпуклых двухмерных и трехмерных телах. Система позволяет создавать модели керамических структур с учетом дефектов. Полученные модели будут использоваться для суперкомпьютерного моделирования ударного нагружения керамик в пакете программ LS-DYNA.

Исследование выполнено в Южно-Уральском государственном университете (национальном исследовательском университете) за счет гранта Российского научного фонда (проект № 14-19-00327).