Разработка стенда для полунатурного моделирования системы управления движением гусеничной машины с гидростатической трансмиссией

В настоящее время системы управления на основе программируемых логических контроллеров (ПЛК) широко используются в различных областях: от систем управления движением до систем распределения электроэнергии, от устройств управления параметрами среды до нефтеперегонных комплексов. На этапе эскизного проектирования систем автоматического управления (САУ) детально прорабатываются возможные варианты алгоритмов управления объектом, а эффективность алгоритмов управления можно установить только по результатам тщательных исследований макетного образца системы.

Отладку алгоритмов обработки информационных сигналов и алгоритмов управления в различных эксплуатационных условиях можно проводить в реальных условиях эксплуатации системы. Однако не всегда есть возможность проведения натурных испытаний, например система управления находится на стадии проектирования; проведение натурных испытаний по настройке и отладке алгоритма работы устройства управления дорого или небезопасно. Замена натурных испытаний математическим моделированием системы тоже не всегда уместна, так как часто алгоритмы управления сложны, громоздки и при математическом моделировании исследователь прибегает к их упрощению. В таких случаях для отладки алгоритмов управления целесообразна организация полунатурного моделирования системы управления [1], при котором часть системы, в том числе само устройство управления, реализуется в виде реальной аппаратуры, например ПЛК, а остальная часть системы (включая объект управления), называемая отброшенной частью системы управления, представляется математической моделью. Благодаря добавлению реальной аппаратуры в контур моделирования сложных процессов, можно добиться уменьшения априорной неопределенности при исследовании процессов, для которых нет полного и адекватного математического описания.

На предприятиях, разрабатывающих системы автоматического управления движением гусеничных подвижных объектов, для сотрудников одинаково важными считаются и навык проектирования алгоритмов управления, и навык программирования ПЛК. Поэтому для таких предприятий актуальной задачей является создание стенда, на котором работники смогут получить практические навыки работы с программируемыми логическими контроллерами в составе системы управления, ознакомиться с особенностями программирования и настройки ПЛК, а также смогут проводить испытания и отладку проектируемых алгоритмов управления движением гусеничной машины.

Анализ известных на рынке технических решений [2–7] показал, что основными недостатками существующих учебно-лабораторных стендов для обучения программированию ПЛК и стендов для отработки алгоритмов управления являются: высокая стоимость (свыше 430 тыс. руб.) при избыточном функционале; закрытая архитектура и связанная с этим сложность масштабирования стенда; скрытое от пользователя устройство и реализация стендового оборудования, что затрудняет процесс обучения; необходимость после покупки стенда в замене модели реализованного на стенде объекта управления на математическую модель конкретной гусеничной машины с гидростатической трансмиссией, а контроллера стенда – на ПЛК, используемый на предприятии, что эквивалентно разработке нового стенда.

Поэтому целью данной работы является разработка аппаратной и программной части учебно-лабораторного стенда для полунатурного моделирования системы управления движением гусеничной машины (ГМ) на базе трактора ТМ-10 на базе контролера Bosch-Rexroth и для отработки алгоритмов управления на стадии их разработки.

Структурная схема учебно-лабораторного стенда представлена на рис. 1.

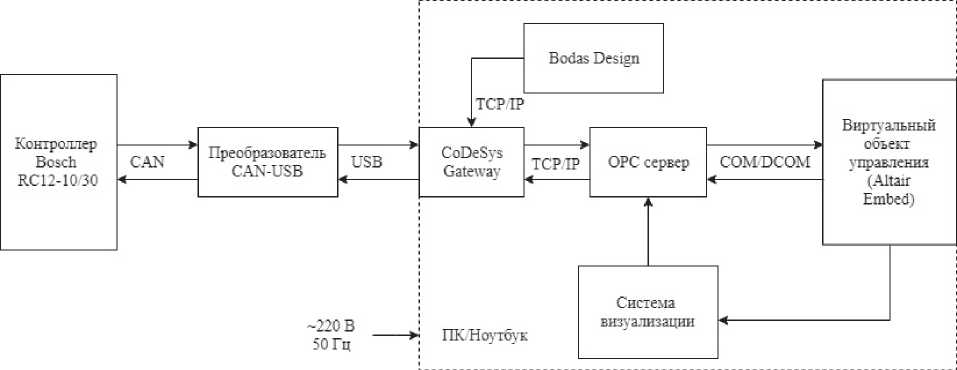
Рис. 1. Структурная схема учебно-лабораторного стенда

В качестве реальной аппаратуры в стенде применяется устройство управления, реализованное на контроллере Bosch RC12-10/30, а также интерфейсный преобразователь CAN-USB CANfox EC2112 как элемент устройства сопряжения с объектом управления. Отброшенной частью системы в учебно-лабораторном стенде является транспортная платформа с двигателем внутреннего сгорания (ДВС), гидростатической трансмиссией (ГСТ), выполненной по бортовой схеме, и гусеничным движителем. Прототипом платформы является промышленный гусеничный трактор класса тяги 15 т производства ОАО «Завод дорожно-строительной техники «Урал», г. Челябинск. Отброшенная часть системы управления ГМ с гидростатической трансмиссией (ГСТ) совместно с имитатором внешних воздействий и задающим устройством реализована на персональном компьютере в программном пакете Altair Embed 2019.

Схема плоскопараллельного движения ГМ, схема моторно-трансмиссионной установки ГМ, а также основные уравнения связей, характеризующие взаимодействие гусениц с грунтом, перераспределение веса машины при повороте по бортам, формирование тяговых усилий на гусеницах, сопротивление прямолинейному движению и повороту ГМ подробно рассмотрены в работах [8–11].

Математическая модель криволинейного движения платформы на плоскости представляет собой систему трех дифференциальных уравнений в форме уравнений Лагранжа второго рода:

^ = [(P2 + P1 — Pf — Pf2) sin ф + R6 cos ф]^

« 0^= [(P2+P1 —Pf1 —Pf2)cOSф —RбSinф]^'                                   (1)

,    = [(P, - P + P f — pf2) 2 - sign 3 MC] £, где Т - текущее время, с; Хс, Yc - координаты центра тяжести ГМ, м; ф — курсовой угол, рад; P 1, P2 - силы тяги на левом и правом бортах; Pf1, Pf2 - сопротивление передвижению на левом и правом бортах; R6 - боковая сила инерции; Мс - момент сопротивления повороту, формирующийся силами и моментами трения; G - вес платформы; /с - момент инерции платформы относительно вертикальной оси, проходящей через центр тяжести; g – ускорение свободного падения.

Моторно-трансмиссионная установка имеет три степени свободы и описывается тремя дифференциальными уравнениями первого порядка [11–13]:

<а0? = [мд - МГН1 - МГН2] 1, а^М1 =

*     ат —

Д^ М2 =

I     ат ~

^М М1

^М М2

—

—

Р 1 Й ВК

,

^• бр      7 2

Р 2 ^ ВК

. 7з '

где ш_ГН, ш_М1, ш_М2 - угловые скорости валов ДВС и моторов ГОП; М д , М_ГН1, М_ГН2 - крутящие моменты на валах ДВС и насосов гидрообъемных передач (ГОП); М_М1,М_М2 - моменты на моторах ГОП; R_BK - радиус ведущего колеса; i_6p - передаточное число бортового редуктора; /₁,/₂,/ з -моменты инерции соответствующих масс.

Гидрообъемные передачи (ГОП) описываются алгебраическими уравнениями для давления в каждой из магистралей [14, 15]:

^а аТ П¹¹ = ^[Qh1 - ^Qm1 - ^Q k11 ^{+ Q} k12 ^{+ Q} kpp11 ^{— Д}^ 11 ^{— Д} 9 м11 ^] ^" ,

ГОП¹² = ^[Qm1 ^{— Q} H1 ^{+ Q} k11 ^{— Q} k12 ⁺ Q kpp12 ^{— Д} @ И12 ^{— ДQ} м12 ^] ;Т'

. ^ат                                                                                          V' ²                                     (3)

^d аТ П²¹ = ^[Qh2 ^{— Q} M2 ^{— Q} k21 ^{— Q} k22 ^{+ Q} kpp21 ^{— AQ}h21 ^{— AQ}m21^] ^ 1 '

< аТ П²² = ^[Qm2 ^{— Q}h2 ^{+ Q} k22 ^{— Q} k22 ^{+ Q} kpp22 ^— △ ^Qh22 ^— △ ^Qm22^] ^ " '

где P_r on ₁₁,P_r on ₁₂ - давления в магистралях нагнетания и всасывания первой ГОП; P_r on ₂₁,P_r on ₂₂ -давления в магистралях нагнетания и всасывания второй ГОП; Q_H1, Q_M1 - расходы насоса и мотора первой ГОП; Q h2 , Q m2 - расходы насоса и мотора второй ГОП; Q kn , Q k12 , Q k21 , Q k22 - расходы предохранительных клапанов; Q_kpp11, Q_kpp12, Q_kpp21, Q_kpp22 - расходы клапанов подпитки; AQ_H, AQ_M — утечки в насосах и моторах; Е — модуль упругости жидкости в магистралях; V 1 , У₂ — объемы соответствующих магистралей.

Связь реальной части системы управления с отброшенной частью осуществляется через технологию OPC. Так, управляющие сигналы с контроллера через преобразователь CAN-USB поступают в ПК (шлюз CoDeSys Gateway), затем сигналы по протоколу TCP/IP передаются в OPC-сервер, и уже оттуда по протоколу COM/DCOM поступают в Altair Embed, где реализована отброшенная часть системы управления движением ГМ. Информационно-измерительные сигналы передаются в контроллер по тому же пути в обратном направлении. Интерфейсный преобразователь CAN-USB CANfox EC2112, шлюз CoDeSys Gateway и OPC-сервер являются составными частями устройства сопряжения с объектом (УСО).

Формирование алгоритмов управления движениемгусеничной машины с гидростатической трансмиссией

Управление движением платформы осуществляется изменением производительности (подачи) насосов ГОП [16]. Гидромоторы имеют два режима – рабочий и транспортный. Иными словами, насосы непрерывно регулируемые, а моторы двухпозиционные. При движении прямо насосы регулируются синхронно, а при повороте уменьшается подача насоса отстающего борта [17].

Одними из наиболее значимых преимуществ ГОП в механизме поворота являются внешняя автоматичность и возможность бесступенчатого регулирования. В работах [18, 19] предлагается использовать обратную связь при регулировании подачи насоса ГОП отстающего борта по отклонению кривизны траектории к ш , задаваемой штурвалом, от текущей кривизны траектории к д , реализуемой ГМ на местности. Регулирование подачи насоса именно по Дк = к ш — к_д позволяет обеспечить движение ГМ по замкнутой траектории независимо от влияния внешних возмущений f со стороны грунта, поскольку стабилизация к_д = R ~\ где R — радиус разворота ГМ, - это, по сути, обеспечение R = const, при f = var.

Структурная схема автоматической системы (АС) управления движением гусеничной платформы приведена на рис. 2.

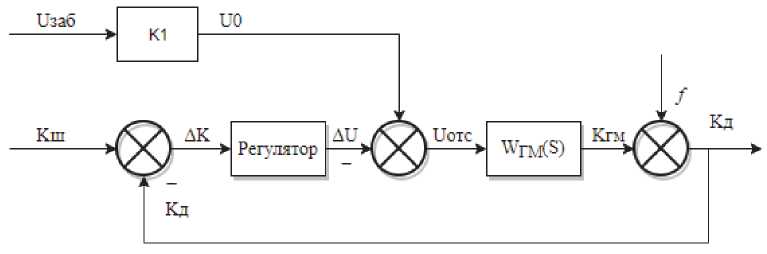
Рис. 2. Структурная схема АС управления движением ГМ: W_rM(s) — передаточная функция ГМ;

f — возмущение (изменение к_ГМ , вызванное влиянием изменяющейся нагрузки со стороны грунта и неучтенными потерями в насосах и моторах ГОП)

Автоматическая система управления подачей насоса отстающего борта работает следующим образом: опорный сигнал П_ЗАБ подачи насоса забегающего борта задает скорость прямолинейного движения платформы. В случае нулевой кривизны проложенной трассы и отсутствия внешних помех движению параметр регулирования подачи насоса отстающего борта П оТс = П_ЗАБ , и платформа движется прямо. При появлении помех, например буксования одной из гусениц, или утечек в одной из ГОП, АС по разности кривизны реальной траектории центра тяжести и заданной линией на местности корректирует подачу насоса отстающего борта и прямолинейное движение восстанавливается. При повороте соотношение П_ЗАБ и П оТс задается кривизной трассы. В качестве регулятора применяется ПИД-регулятор с возможностью настройки его параметров в системе визуализации. Единичная обратная связь и регулятор обеспечивают точное соответствие кривизны траектории центра тяжести проложенной на местности линии маршрута.

Параметр регулирования подачи насоса отстающего борта определяется следующим образом:

ПОТС = к1 • ПЗАБ — [кП • (Дк) + кИ • J(Дк')dt + кдиф ^)],                                 (4)

где

^/к ^-В/г

к1=тг^вт.                                                            (5)

/кш+ /2

к П , к И , к диф — настроечные параметры пропорциональной, интегральной и дифференциальной составляющей регулятора соответственно.

Текущая кривизна траектории к_д вычисляется как отношение угловой скорости поворота машины ш_м, измеряемой вибрационным датчиком угловой скорости - микромеханическим гироскопом, к продольной скорости центра тяжести машины У_м, оцениваемой по частоте вращения выходного вала коробки передач.

^к д =^. (6)

Параметры и_ЗАБ и U o _T c соотносятся с параметрами регулирования насосов первого и второго ГОП и_Н1,и_Н2 в зависимости от знака кривизны штур в ала к ш . Таким образом, при пов о роте направо (к ш >  0) насос второго ГОП, расположенного на левом борту гусеничной машины, является насосом забегающего борта, то есть ы_Н2 = и_ЗАБ, а насос первого ГОП, расположенного на правом борту ГМ, является насосом отстающего борта, то есть ы_Н1 = U_0T c . При повороте налево (к ш <  0) забегающим бортом является правый борт ГМ, а отстающим - левый: ы_Н1 = и_ЗАБ, ы_Н2 = U o _T c .

В [19] показана эффективность раздельной работы тормозов при угрозе заноса и при перегрузке ГОП по давлению. На основе данной работы сформированы алгоритм включения тормоза забегающего борта при угрозе заноса и алгоритм включения тормоза отстаю щ его борта при перегрузке гидрообъемного механизма поворота по давлению.

Тормоз на забегающем борту включается в звонковом режиме при превышении текущей кривизны траектории к_д, реализуемой ГМ на местности, над кривизной тра е ктории к ш , задаваемой штурвалом, на величину, равную или большую е.

Тормоз на отстающем борту включается в звонковом режиме при достижении относ и тельного давления в магистрали ГОП отстающего борта – 80 % от максимально допустимого давления.

Для удобной работы на учебно-лабораторном стенде была разработана система визу а лизации в графической среде Altair Embed, представляющая собой графический интерфейс польз о вателя.

На мнемосхеме панели оператора (рис. 3) демонстрируются графики изменения: скорости центра тяжести; траектории движения центра тяжести; параметров регулирования подачи насоса ГОП1 и ГОП2; кривизны траектории (заданной и текущей); скорости вращения гусениц на левом и правом бортах; коэффициента сопротивления грунта под каждой гусеницей.

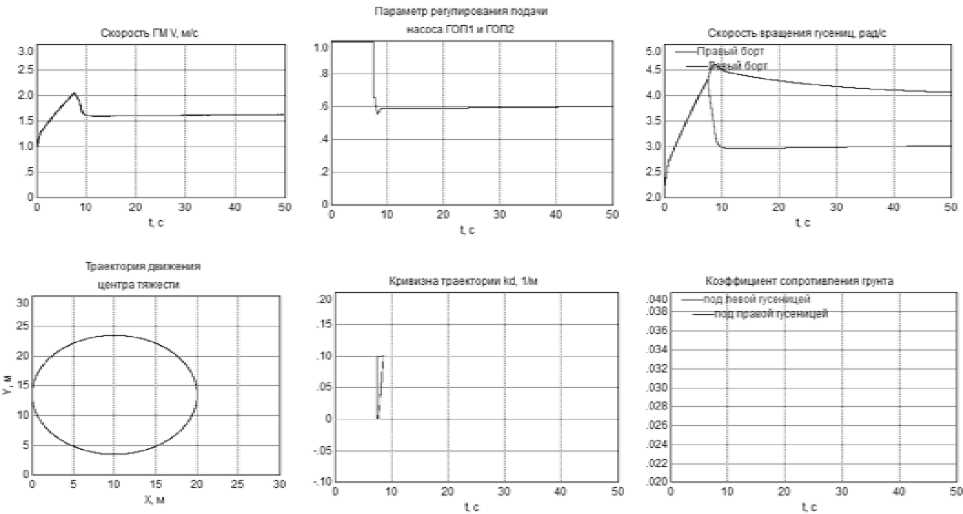
Рис. 3. Мнемосхема панели оператора

С помощью панели выбора траектории движения ( рис. 4) устанавливается один из вариантов изменения траектории движения во время моделирования. Для каждого типа траектории движения выполнены два варианта реализации: зависимость от времени и зависимость от пут и . На панели можно выбрать один из вариантов реализации и установить настроечные параметры.

На панели настройки алгоритмов управления движением гусеничной машины (рис. 5) задается тип регулятора, используемый в алгоритме управления, и выбираются его настроечные параметры. Также на панели активируются или деакт и вируются алгоритмы включения тормоза на забегающем или отстающем борту и выбираются настроечные параметры для работы алгоритмов.

! ) Прямолинейное движение

( ) Движение по кругу

Движение по "змейке"

( ) Маневр "перестроение"

( ) Среднестатистическая трасса

( ) Произвольная траектория

Кривизна траектории Krd = | 0.1 |

Промежуток между поворотами (по умолчанию: 8=10,1=10)

Функция времени	Функция пути
s = ГтГ|

Рис. 4. Панель выбора траектории движения

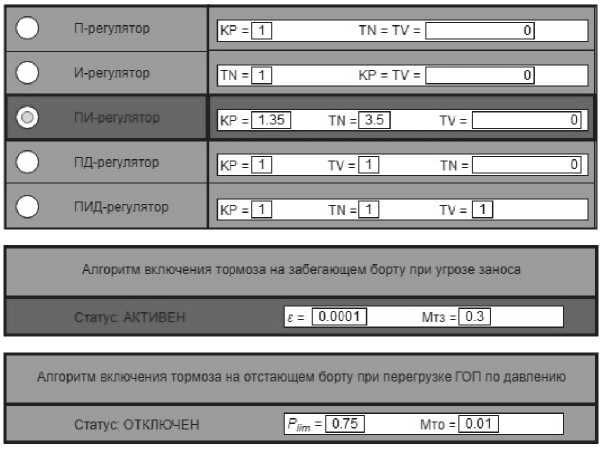
Рис. 5. Панель настройки алгоритмов управления движением гусеничной машины

Меняющийся грунт

Разовое изменение

Начальное значение

0 05

Правая гусеница

Левая гусеница

Изменение по пройденному пути

Асфальт

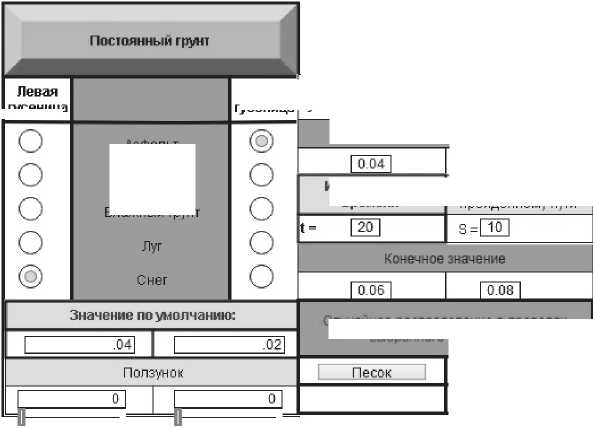
Рис. 6. Панель настройки параметров грунта

гусеница

Правая гусеница

Сухой грунт

Влажный грунт

Изменение по времени

Случайное распределение в пределах выбранного типа грунта

Г Су хой грунт ^

На панели настройки параметров грунта (рис. 6) организована возможность выбора пользователем того, будет ли меняться коэффициент сопротивления грунта во время моделирования. Для «постоянного грунта» пользователем выбирается тип грунта под каждой гусеницей, а также устанавливается значение его коэффициента сопротивления «по умолчанию» или на определен- ном уровне в пределах допустимого диапазона изменением положения ползунка в соответствующем поле. Для «меняющегося грунта» выбирается режим разового изменения грунта под каждой гусеницей в зависимости от времени моделирования или пройденного пути и устанавливаются начальное и конечное значения коэффициента. Также пользователь может выбрать режим случайного распределения значения в пределах выбранного типа грунта и установить необходимый тип грунта для каждой гусеницы.

Заключение

Разработан и реализован стенд для полунатурного моделирования системы управления движением гусеничной машины ТМ-10 с гидростатической трансмиссией, предназначенного как для обучения программированию ПЛК Bosch RC12-10/30 , так и для тестирования алгоритмов управления движением машины на стадии их разработки. Под потребности стенда адаптирована математическая модель системы управления движением гусеничной машины, сформирован комплекс алгоритмов управления, включающий алгоритм управления движением гусеничной машины, алгоритм включения тормоза забегающего борта при угрозе возникновения заноса и алгоритм включения тормоза отстающего борта при перегрузке гидрообъемного механизма по давлению.