Разработка технологии упрочнения абразивных кругов на керамических связках

В начальный момент времени т. 1 и 1' при Θ исх

T ⋅ d _H

= 20 oС оправка имеет размер d“cp ± 2 , а отвер- стие круга

d acp

T ⋅ d ±

, посадка осуществляется с зазором Δ з.ср.. Дальнейшее нагревание приводит к тому, что зазор уменьшается. Температура, при которой Δз = 0, назовем температурой равновесия Θ 1, это соответствует (рис. 1) точкам 2 и 2'. Когда температура достигнет максимальной величины

Θ ₁ , оправка увеличит свой размер до т. 3, в тоже время отверстие абразивного круга увеличится только до т. 3', создавая при этом расчетный натяг Δ _н.ср. Фактически натяга не будет, т.к. в результате диаметра металлической оправки σ Θ практически равны нулю.

Это связано с тем, что абразивная масса при- обретает при Θ Т = 12500С вязкотекучее состояние и диаметр отверстия круга без особых усилий трансформируется в диаметр оправки (точка 4’). В процессе охлаждения металлическая оправка из точки 4 переходит в т.5, сохраняя исходный размер и допуск, а отверстие абразивного круга, охлаждаясь, уменьшается только до т.5 и не возвращается в исходное состояние, т.е. dа.ср.› становится больше dа.ср.. Анализ схемы полей допусков при контактирования заготовки круга с оправкой показывает, что величины среднего зазора и натяга можно рассчитать по формулам:

^∆ 3 cp ^{= d}acp ^⋅Θ 1 ^⋅ ( α M 1 ^- α a 1 ) ,      (1)

∆ _Hcp = d _acp ⋅ ( 1 +Θ ₁ ⋅ α _{a 1} ) ⋅ ( Θ _T -Θ ₁ ) ⋅ ( α _M - α _a ) ,(2)

где d _а.ср. – средний диаметр отверстия абразивного круга; α _M , α _{M 1} , α _a , α _{a 1} – соответственно коэффициенты термического расширения металлической оправки и круга при температурах Θ _T и Θ ₁ .

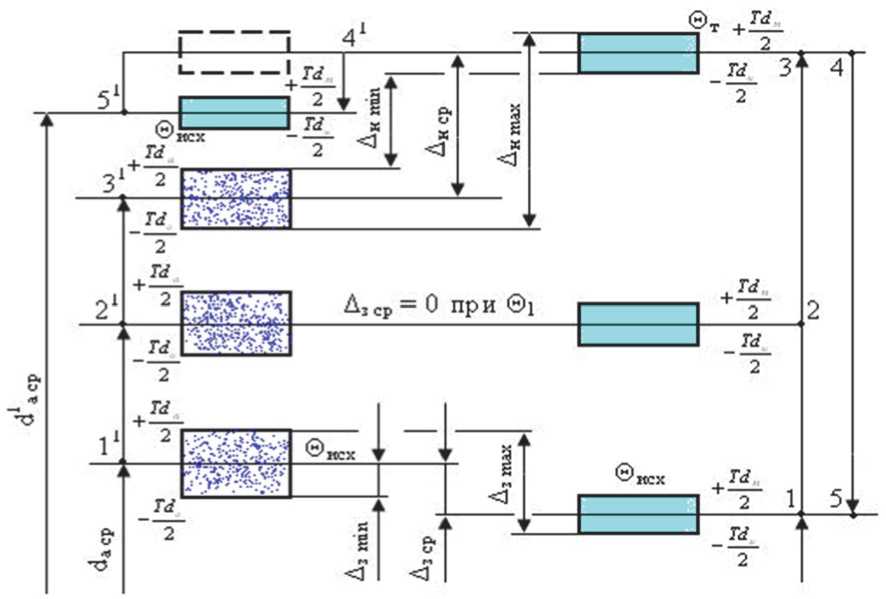
Рис. 1. Схема полей допусков отверстия абразивного круга и металлической оправки при упрочнении

Диаметр отверстия абразивного круга после термообработки:

dacp = d м. cp ' (1 + 0 T " aM У (1 - 01 " aa ) , (3)

и диаметр металлической оправки расчетный:

,                (4)

м.cp      acp 3cp а также для получения точного размера отверстия:

'

м . cp

d acp

(1 + 0tаH1 -©i • а)’

В результате увеличения расчетного значения диаметра отверстия dacp необходимо определить диаметр сердечника пресс-формы dacp , который после упрочнения был бы равен dacp

, a.c.        acp           a ,

, T • d M

2    , т.е.

где '

^ ^da = ^dacp ^{- d}acp = ^dMcp '⁽¹ + ⁰ T ‘ « M M¹ - ⁰ 1 ‘ “ a ^{)- d}acp .

Тогда:

da.c. = 2dacp - dM.p • (1 + 0T • «M )• (1 -01 • «a ) - (7)

Это значение можно определить и по приближенной формуле:

d ~ с!*., — Д7 , a .c.      Mcp       3cp ,

Одним из важных факторов, определяющих величину натяга и зазора, является величина коэффициента термического расширения. Зная коэффициент термического расширения метал- лической оправки а м и абразивного круга а а при различных температурах, можно рассчитать основные параметры процесса упрочнения. Для исследования процесса упрочнения с помощью программы ANSYS построена модель, в которой стояла задача смоделировать процесс упрочнения шлифовального круга и теоретически определить остаточные напряжения и деформации после охлаждения. Решение данной задачи основано на методе конечных элементов. При моделировании учитывались свойства материалов круга и оправки: линейные свойства: модуль упругости, коэффициент Пуассона [1], нелинейные свойства: предел текучести и касательный модуль (только для материала круга), коэффициент линейного расширения материалов [1].

Как показано на рис. 2, остаточные напряжения в круге после снятия нагрузки распределены неравномерно. Наибольшие остаточные напряжения возникают на внутреннем диаметре круга ( <г ₀ = 18МПа), что является следствием натяга при соприкосновении оправки и круга, к середине круга ( с ₀ = 4,31МПа) напряжения уменьшаются. К периферии круга ( с₀ = 9,9МПа) происходит снова увеличение величины напряжений, т. к. вступает в силу теория равновесия тел.

Так как материал круга обладает пластическими свойствами, после снятия нагрузки остаются пластические деформации. Максимальные деформации возникают на внутреннем диаметре круга. В радиальном направлении величина де-

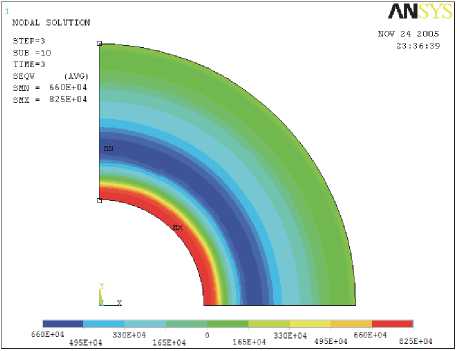
Рис. 2. Остаточные напряжения в круге после снятия нагрузки (охлаждения)

формаций уменьшается и на поверхности круга становится минимальной. На рис. 3 показаны пластические деформации, из которых видно, что круг деформируется лишь в небольшой части у отверстия круга. Отсюда можно сделать вывод, что этими деформациями можно пренебречь.

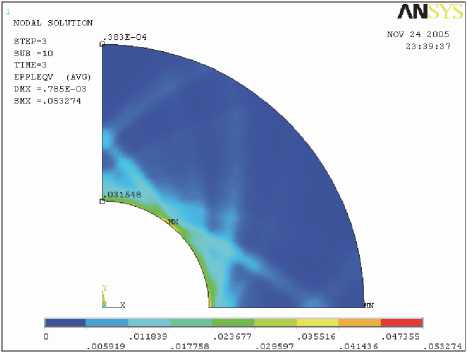
Рис. 3. Пластические деформации в круге после снятия нагрузки (охлаждения)

Исследования показали, что при упрочнении сплошной металлической оправкой контакт оправки с отверстием круга происходит неравномерно, так как отклонение от округлости отверстия после сушки 0,3-0,7 мм, а эта величина соизмерима с величиной натяга при нагреве. Поэтому предложен способ упрочнения разрезной металлической оправкой. Величина разреза кольца компенсирует отклонения формы заготовки круга при прессовании и рассчитывается из условия полного контакта круга с кольцом, при температуре 750 oС.

Методика расчета параметров упрочнения аналогична методике, приведенной ранее. Но, так как оправка имеет разрез, который начинает смыкаться при Θ = 600 ^oС (соприкосновение оправки и круга), необходимо его рассчитать таким образом, чтобы при смыкании полностью паза при некоторой температуре 600 ^oС <  Θ < 1250

^oС, создавался натяг такой, чтобы, дойдя до Θ _Т = 1250 ^oС оправка имела размер d _м равный диаметру посадочного отверстия по ГОСТ.

Размер круга при Θ = 750⁰С:

dа2 = dа1 · (1 +( Θ2 – Θ1) Θа2),(9)

где d _а1 – диаметр отверстия АК при 600 ^oС, Θ ₁ = 600 ⁰С, Θ ₂ = 750 ^oС.

Диаметр оправки при Θ ₂:

dм2 = dм исх ×(1 + Θ2 × Θм2),(10)

Тогда ширина разреза оправки:

∆Н = (dм2 – dа2) π,(11)

Создаваемый натяг при нагреве от 750 oС до

1250 oС:

∆нср = dмТ – dа 2,(12)

В интервале Θ ₁ = 20 ⁰С – 600 ^oС происходит касание оправки с кругом. Затем до Θ = 600-750 ^oС начинает смыкаться паз оправки. Полное смыкание паза происходит при Θ ₂ = 750 ^oС. В интервале 750 ^oС - 1250 ^oС формируется натяг. На рис. 4 показана схема для расчета исходных данных при построении модели упрочнения круга разрезной оправкой.

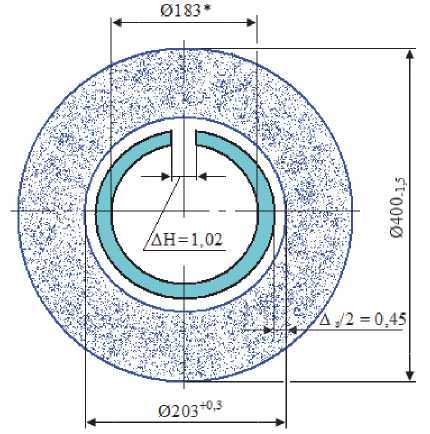
Рис. 4. Схема для расчета; * – размер для справок

Из рис. 5 видно, что картина перераспределения остаточных напряжений аналогична предыдущей модели. Происходит максимальное увеличение напряжений на внутреннем диаметре круга, затем их величина уменьшается и к периферии снова возрастает. Пластические деформации абсолютно идентичны предыдущей модели, т.к. ни материал круга, ни материал оправки – не меняются.

Исследование процесса упрочнения производилось по приведенной методике на кругах 24А16НСМ16К5 А400×203×8. Круги упрочнялись с помощью как сплошной, так и разрезной оправки в печи туннельного типа с режимами по технологии: нагрев до 1250 oС в течение 3 ч, затем выдержка при данной температуре. Осты-

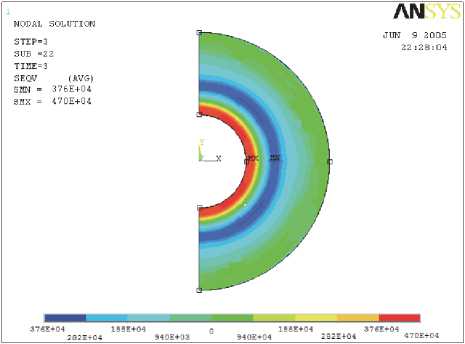
Рис. 5. Остаточные напряжения в круге после снятия нагрузки (охлаждения) вание абразивного круга вместе с упрочняющей оправкой до температуры 20 ^oС в течение 3 ч. Затем оправка вынималась и использовалась вновь. На рис.6 представлены эпюры остаточных напряжений кругов, замеренные после упрочнения сплошной и разрезной оправками.

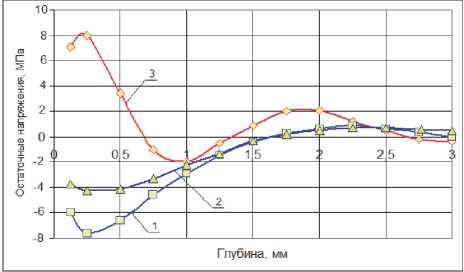
Проведенными исследованиями установлено, что применение сплошной металлической оправки с натягом ∆ _нср. = 2,9 мм формирует в поверхностном слое отверстия абразивного круга остаточные напряжения сжатия величиной 6-8 МПа. Отсюда можно сделать вывод, что существует взаимосвязь деформации внутренней поверхности круга и формировании в поверхностном слое остаточных напряжений сжатия σ_Θ = 5-6 МПа. При упрочнении кругов разрезной оправкой, в отверстии формируются напряжения сжатия σ_Θ = 3,8 – 4,5 МПа, на рабочей поверхности σ_Θ = 3,7-4,0 МПа. Для обычных кругов без вставки за счет интенсивного охлаждения отверстия возникают временные напряжения растяжения. Это связано с тем, что участки круга, прилегающие к отверстию, кристаллизуются раньше, уменьшая свой объем, чему препятствуют вышележащие слои. После остывания круга по всему объему в зависимости от интенсивности внутренних и временных напряжений будут формироваться остаточные напряжения. Знак этих напряжений, как было показано ранее, связан с продольной и поперечной усадкой гранул в процессе термообработки. Для кругов зернистостью 16 и более, формируются остаточные напряжения растяжения, а для зернистостей 12 и меньше - сжатие. Важно заметить, что в случае применения упрочняющей термообработки общая картина изменяется независимо от зернистости абразивного инструмента.

Рассмотрим механизм образования остаточных напряжений при упрочнении. Под действием напряжений, вызванных натягом, зерна, окруженные связкой, приобретают радиальное перемещение. При этом расстояние между центрами зерен в одном направлении уменьшается и связка,

б

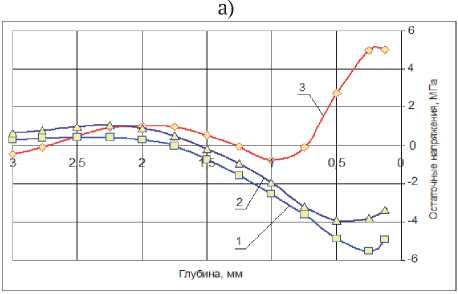
Рис. 6. Распределение остаточных напряжений в круге 24А16ПСМ16К5, упрочненном сплошной оправкой 1 , разрезным кольцом 2 и неупрочненном 3 :

а – у отверстия, б – на рабочей поверхности окружающая зерно, приобретает эллипсоидную форму, поэтому большая ось эллипса ориентируется перпендикулярно радиусу. Это приводит к уменьшению пористости в упрочненном слое за счет увеличения количества связки и изменению формы пор, которые становятся также вытянутыми. Согласно гидродинамической теории смазки расстояние между частицами уменьшается до тех пор, пока не установится минимально допустимое сближение ∆ min. Затем появляется сдвиг одного зерна относительно другого и изменяется упаковка зерен и увеличивается плотность данного слоя. При термообработке этот слой увеличивает свою длину в большей мере, чем в обычных кругах, чему препятствуют вышележащие слои, которые формируют сжимающие технологические напряжения. В результате охлаждения упрочненный слой первый приобретает кристаллическую структуру и уменьшает свой объем, действует так называемая усадка. Этому процессу препятствуют слои, которые расположены глубже, они вызывают в этом слое растягивающие временные напряжения, которые по своей величине меньше сжимающих технологических. Поэтому после того, как связка на внутренней части круга приобретает твердое состояние и произойдет ее усадка, на поверхности отверстия в упрочненной зоне сформируются остаточные напряжения сжатия. На их величину и глубину проникновения оказывают влияние температура, как функция коэффициента теплоотдачи и геометри- ческие размеры абразивного круга. Кроме этого наличие металлической оправки при термообработке увеличивают скорость охлаждения отверстия в круге в диапазоне температур от 1250 оС до 1000 оС. Как известно, [2] скорость охлаждения влияет на кристаллическую структуру связки. При скорости охлаждения более 200 оС в час в начальный момент охлаждения в связке образуется мелкокристаллическая структура, которая дополнительно уменьшает ее плотность и увеличивает объем упрочненного слоя. Напряжения, которые возникают при этом, имеют один и тот же знак, поэтому напряженное поле сжатия, полученное в результате упрочнения – передеформирует термические напряжения. Таким образом, при упрочнении указанными способами в поверхностных слоях отверстия круга и на периферии, формируются остаточные напряжения сжатия, величина которых зависит от характеристик абразивного круга и режимов упрочнения. Были проведены исследования упрочненных кругов различной твердости от М2 до С1.

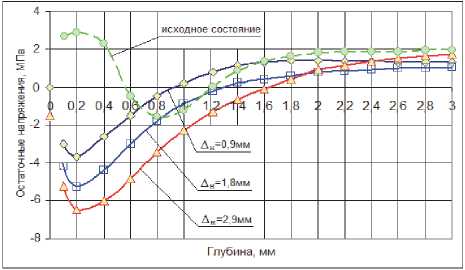
Рис. 7. Влияние натяга на величину остаточных напряжений на рабочей поверхности при упрочнении круга 24А16НСМ1К5 (эксперимент)

Установлено, что с повышением твердости связки от М2 до С1 для 24А16ПК5 величина a _{0 ( r} ) сжатия повышается с 2,5 МПа до 4,5 МПа. Уменьшение зернистости до 8 увеличивает сжимающие напряжения на 2-3 МПа. На рис. 7 показано влияние натяга на величину g _{@ ( r} ) .

В итоге модно сказать, что суммарные напряжения в круге увеличиваются с повышением скорости круга. Испытания кругов на разрыв подтвердили, что при приближении Vраб к [Vкр]: σΣ ⇒ [σð]. Однако для упрочненного инструмента величина σ∑ имеет отрицательное значение за счет наведенных в отверстии сжимающих остаточных напряжений, т.е. появился у круга запас прочности, который позволяет при Vк = 68 м/с достигнуть значения σ∑ = 0 (рис. 8). Найдем критическую скорость круга, при которой произойдет разрыв кругов, изготовленных по разной технологии. Для этого по оси ординат отложим значение прочности круга на разрыв σp . Эта прямая пересечет зависимости 1, 2 и 3 в точках 1, 2, 3, опустив перпендикуляр из этих точек на ось скорости, получим значение Vкр точки 1', 2' и 3' для каждой технологии изготовления круга.

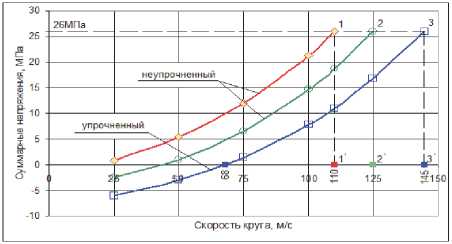
Рис. 8. Зависимость σΣ от скорости вращения круга 24А16НСМ1К5

Если не учитывать остаточные напряжения и рассчитать по формуле:

σ∑ =σω+σR, (13)

то получим точку 1' и V _кр = 110 м/с, для не упрочненного круга, но с учетом ^G @ < r ) (точка 2') величина V _кр = 125м/с, а для кругов с упрочняющей термообработкой (точка 3') V _кр = 145 м/с, т.е. критическая скорость разрыва возросла на 2535 м/с (рис. 8).

Напряжения, возникающие в работающем абразивном круге, связаны с действием ряда фактов: центробежных сил, сил резания, сил закрепления на шпинделе станка, дисбалансом круга, а также напряжений, имеющих термическое происхождение. Как доказано, остаточные напряжения оказывают существенное влияние на напряженное состояние инструмента при работе и должны суммироваться с рабочими от действия центробежных сил и сил резания, которые оказывают влияние на прочность и работоспособность круга. Суммарные напряжения будут равны:

σ _∑ = σ_ω + σ _R + σ _T , (14) где σ_ω – напряжения, вызванные центробежными силами, σ _R – напряжения от сил резания, σ _T – термические напряжения.

Расчеты показали, что эффект упрочнения кругов наблюдается при различных характеристиках абразивного инструмента. Установлено, что с увеличением твердости круга критическая скорость разрыва [Vкр] повышалась и для упрочненных, и для не упрочненных кругов. Необходимо учитывать, что круги данных типоразмеров работают при скоростях до Vк = 60 м/с, а проверяют их на разрыв при Vк = 90 м/с. Применение упрочняющей технологии даже с небольшим натягом ∆ н = 1 мм повышает скорость круга Vк на 10-15 м/с. Максимальный натяг в нашем случае составил ∆ н = 2,9 мм (рис. 8). Круги, упрочненные с данными параметрами, увеличили Vкр на 30 м/с, т.е. в 2 раза. Также установлено, что влияние твердости круга на [Vкр] не меняется во всем диапазоне зернистости. Замечено, что для зернистости 8 – эффект упрочнения больше, чем для зернистости 16 и более. Это, на наш взгляд, объясняется продольной и поперечной усадкой гранул при термообработке. Анализ экспериментальных результатов показал, что эффект упрочнения не зависит от марки абразивного зерна и проявляется как на плавящей связке К5, так и на спекающей связке К3. Кроме этого установлено, что для АК из 24А применение связки К3 уменьшает [Vкр] на 15-20 м/с.

ВЫВОДЫ

Исследование работоспособности доказало влияние натяга при упрочнении на величину критической скорости разрыва. При увеличении натяга с 0,9 до 2,9 мм, критическая скорость разрыва увеличивается 118 до 145 м/с в диапазоне средней твердости СМ1 – СМ2, что на 20 и 45% выше по сравнению с неупрочненными кругами из 24А.