Разработка ультразвуковой измерительной системы для диагностики дефектов зоны сплавления в слоистых материалах

Акустические волны ультразвукового диапазона широко используются в диагностике металлов (см.: [4; 6]). В настоящей работе рассматривается ультразвуковая измерительная система для диагностики слоистых металлических образцов, изготовленных методом сварки взрывом, с использованием оптимальных параметров диагностики. Слоистые металлические структуры находят широкое применение в тяжелом машиностроении, нефтяной, газовой и атомной промышленности, а также других отраслях народного хозяйства.

Покажем теоретический механизм распространения ультразвуковой волны в слоистых металлических структурах, изготовленных методом сварки взрывом. Рассмотрим распространение плоской гармонической акустической волны с частотой р в неоднородной по координате z среде.

Решение уравнения Гельмгольца для давления:

. v + k ²V - 0               (1)

ищем в виде:

V ( x,z ) - Ф ( z ) exp Qk II z ) .          (2)

Здесь k _II – проекция волнового вектора на ось x .

Для зависящей от z функции получаем уравнение:

. i ⁺ k 2 i = 0 ,                 (3)

где

ω kz - Vk2 - k2-, k - “,          (4)

c_l – скорость звука в среде.

Для проекции скорости [2] получаем:

v _z

1 dji i ωρ ₀ dz .

Здесь i0 - плотность среды.

Вводим обозначения:

ш

Q ( z ) =

C i ⁽ z ) ф I v z ⁽ z ) ^ ,

л

A

C 0 ^ k² ^ ^kz I ®p 0

®P 0 ф

0 X .    (6)

^

Тогда уравнения для i(z) и vz(z) записываются в векторном виде: ш dQ - iA Q.            (7)

dz

Для этого уравнения по методу, изложенному в работе авторов [5], получаем следующую характеристическую матрицу:

M ( z ) -

С

n

-

cos(λ₁ z )

ib ₁ sin(λ₁ z )

- -i - sm^ z ) $ b i          ? . (8)

cos(^ i z ) ^

Здесь

k

^ ^- k z , b i ^-   -.           (9)

ωρ0

Рассмотрим теперь систему, состоящую из n -слоев.

Для характеристической матрицы многослойной системы получаем следующий результат:

M ( z „ ) - у М , ( z,- z,_ 1 ) .       (10)

1 - 1

Здесь d_j=z_j–z_j–1 – толщина слоя, а

M , ( z, - z_r 1 ) - соответствующая характеристическая матрица j -го слоя (рис. 1).

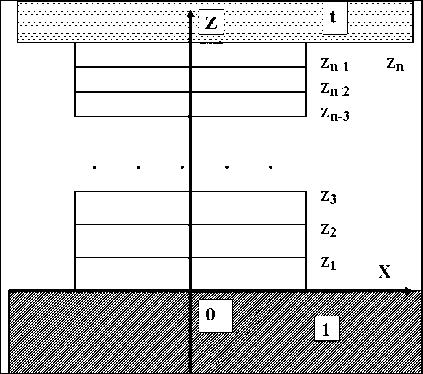
Рис. 1. Многослойная система из n -слоев:

1 – область пространства, откуда приходит волна; t – подложка;

zj – координаты границ слоев;

d_j=z_j–z_j–1 – толщина слоя

Рассматриваем теперь задачу об отражении звуковой волны на границе раздела 2 сред (рис. 2).

Для волн давления и скорости падающей ( i ), отраженной ( R ), прошедшей ( T ) соответственно имеем:

• i ,    - A о exp( ik 1 z z ), i r - A

i t - A t exp( ik z ( z - z „ ))

k vz - A0 1z-exp(ik 1 zz)

ωρ1

k vz -- ar — exP(ik 1 zz)            (11)

ωρ1

k vz - At — exp( iktz (z - z„)) ωρt

Здесь индексы 1 и t относятся к первой среде и подложке соответственно (рис. 2).

Рассматривая сшивание полей на границе среды, получаем следующие формулы для амплитудных коэффициентов отражения и прохождения:

R_A R _ b 1 ⁽ m 11 ⁺ b_tm 12 ) ^{- (} m 21 + b_tm 22 )     (12)

A 0    b 1 ⁽ mu ⁺ b t m 12 ) ^{+ (} m 21 ⁺ b t m 22 )’

_T   A T                2 b 1

A ₀    b 1 ( m 11 + b_tm ₁₂) + ( m ₂₁ + b_tm ₂₂)

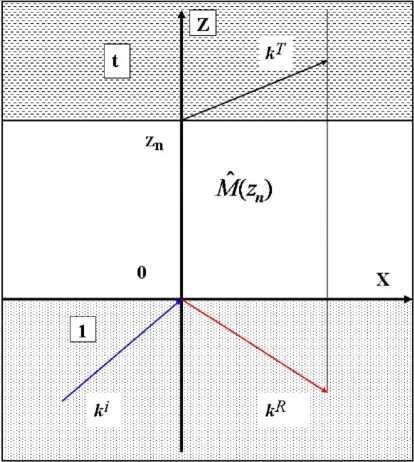
Рис. 2. Геометрия отражения звуковой волны на границе раздела 2 сред: волновые векторы волн давления падающей ( i ), отраженной ( R ), прошедшей ( T );

M ( z _n ) – характеристическая матрица многослойной структуры

Здесь m_ij – элементы характеристичес- k tz кой матрицы слоистой системы, b t _ю р .

Для энергетических коэффициентов от- ражения и прохождения получаем:

в = |л|2,                  (14)

А

ρ₁ Re k_tz

ρ _t Re k _{1 z}

На рисунках 3 и 4 представлены частотные спектры отражения и прохождения для различных случаев при нормальном падении. Видно, что частота 2,5 МГц попадает в область минимального отражения для параметров рисунка 3, что является приемлемым. При другом значении параметров иммерсионного слоя отражение будет гораздо более значительным – 75 % (рис. 4), что значительно затрудняет диагностику дефекта. Таким образом можно подобрать оптимальные параметры этого слоя. Из рисунков видна интерференция волн из-за слоистости системы. При этом характер интерференции определяется размерами слоев и характеристиками их материалов.

Рассмотрен также случай, когда биметаллический слой содержит дефект в виде тонкого воздушного слоя. Рассматривались случаи биметаллов сталь + сталь, медь + сталь.

Анализ спектров отражения показывает, что наличие дефекта дает эффект полного внутреннего отражения: для всех частот из рассматриваемого диапазона энергетический коэффициент отражения равен 1, соответственно, коэффициент прохождения равен 0. Поэтому его легко обнаружить экспериментально.

На рисунках 5 и 6 приведены графики зависимостей фазы отраженной волны. Последний рисунок относится к случаю, когда биметаллический слой содержит дефект в виде тонкого воздушного слоя. Из этого графика видно, что хотя энергетический коэффициент

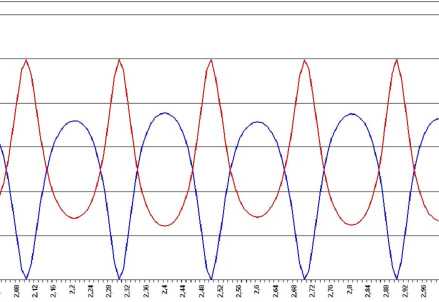
Рис. 3. Частотные спектры энергетического коэффициента отражения (синий) и прохождения (красный) для параметров иммерсионного слоя c = 4000 м/с, с = 3000 кг/куб.

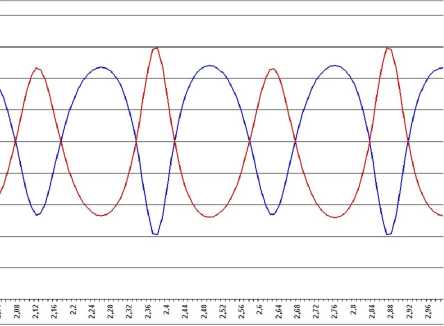
Рис. 4. Частотные спектры отражения и

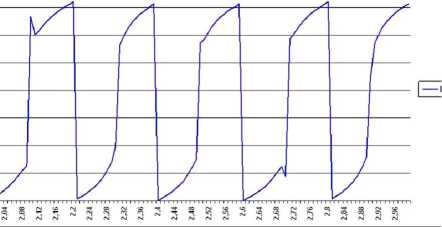
Рис. 5. Частотная зависимость фазы отраженной волны для параметров рис. 3

прохождения для параметров иммерсионного слоя c = 5000 м/с, с = 4000 кг/куб. м

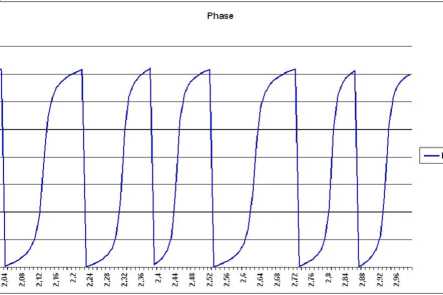
Рис. 6. Частотная зависимость фазы отраженной волны. Случай биметаллического слоя с дефектом в виде тонкого воздушного слоя

отражения равен 1, фаза продолжает сохранять чувствительность к наличию границ многослойной системы.

В настоящей работе были проведены эксперименты по диагностике дефектов в биметаллах с использованием результатов теоретического анализа и найдены оптимальные параметры для обнаружения дефектов слоистой структуры. Для этого нами была построена измерительная система для диагностики слоистых металлических образцов, изготовленных метом сварки взрывом, с использованием современных ультразвуковых дефектоскопов УД2-140 и УД2-70, в которых реализованы импульсные варианты эхо-метода и зеркально-теневого метода, с последующей обработкой полученных данных.

Для проведения ультразвуковой диагностики были разработаны и изготовлены наклонные пьезоэлектрические преобразователи с углами ввода в сталь 65° и 50°, с частотой ультразвукового импульса 2,5 МГц, для которых построены реверберационно-шумовые характеристики, сняты амплитудно-частотные характеристики, а также в работе использовались стандартные раздельно-совмещенные пьезоэлектрические преобразователи с частотами 2,5 и 5,0 МГц. Частота повторения ультразвуковых импульсов фиксирована и равна 1 кГц. На рисунках 7, 8 и 9 представлены дефектограммы, характерные для различных параметров дефекта в граничной зоне металлических слоев.

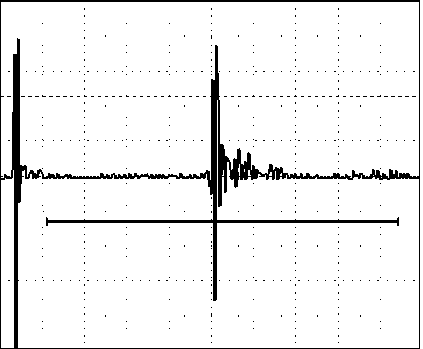
Рис. 7. Отражение импульса от зоны сплавления в отсутствие дефекта

(слоистая металлическая структура сталь + сталь)

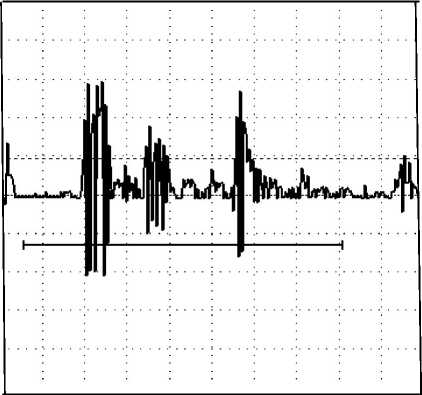
Рис. 8. Отражение импульса от дефекта размером 0,01 мм (слоистая металлическая структура сталь + сталь)

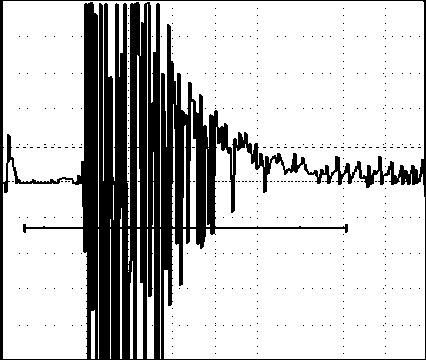
Рис. 9. Отражение импульса от дефекта размером 0,1 мм (слоистая металлическая структура сталь + сталь)

Таким образом, в работе построена ультразвуковая измерительная система для экспериментального анализа отражения ультразвуковой акустической волны для различных слоистых металлических образцов, изготовленных методом сварки взрывом. Одновременно построена математическая модель распространения ультразвуковой волны в слоистых металлических структурах. Полученные результаты показывают эффективность данного подхода при диагностике слоистых систем.