Разработка веб-приложения для эксперимента по восстановлению спектра нейтронов с применением алгоритмов нейронный сетей

Белый А. А., Стариковская М. Д., Чижов К. А. Разработка веб-приложения для эксперимента по восстановлению спектра нейтронов с применением алгоритмов нейронный сетей // Системный анализ в науке и образовании: сетевое научное издание. 2025. № 2. С. 49-57. EDN: XQZWTL. URL:

4.0)

Радиационный контроль на ускорителях частиц не может быть произведен с помощью стандартных дозиметров и радиометров нейтронов, так как их рабочий диапазон ограничен максимальной энергией нейтронов около 20 МэВ. На современных высокоэнергетических ускорителях в объединённом институте ядерных исследований (ОИЯИ) энергии нейтронов могут достигать нескольких сотен МэВ и более [1].

Известно, что нейтроны с энергиями более 0,1 МэВ дают основной вклад в эффективную дозу персонала, поэтому, в первую очередь, необходимо обеспечить дозиметрию нейтронного излучения. В связи с вышеупомянутыми ограничениями, для высокоэнергетических установок становится необходимым применение специализированных инструментов, таких как многошаровой спектрометр Боннера. Получение спектров и доз – это сложный процесс вычислений, который требует специализированного математического аппарата и программного обеспечения [1].

Показания спектрометра Боннера связаны со спектром нейтронов через уравнение Фредгольма 1го рода (см. формула 1):

Q i =

f.....

^mm

K^EEpd^dE =

г lu ln(10) I  Kj(u)v(u)E(u)du,

J 0

j = 1..... m,

где Q j - показание спектрометра Боннера для j-й сферы; K j (E) - ядро j-го уравнения, являющееся функцией чувствительности детектора (непрерывные неотрицательные функции на [E_m i _n, E_max]); ((E) - энергетический спектр нейтронов, Е - энергия нейтрона; пределы интегрирования E_m i _n и E_max определяются областью определения спектра и используемого для измерений набора детекторов (для наших данных E_min = 10^-3 эВ и Е_тах = 3,98 • 10⁸ эВ), l_u = gf ^E ) .. Поскольку ^lg(E min )

восстановление спектра нейтронов предполагается в широком диапазоне энергий, превышающем несколько порядков, для уменьшения погрешности численного интегрирования удобно перейти к новой безразмерной переменной, называемой летаргией u(E) = lg(E—).

Однако с математической точки зрения задача восстановления спектра нейтронов по результатам нескольких измерений является некорректно поставленной, поскольку допускает множество решений из-за ограниченного количества шаров-замедлителей и погрешности в исходных данных. Такую задачу в основном решают численно переходом к системе линейных алгебраических уравнений (СЛАУ) с разбиением ((E) по дискретной сетке с шагом ДЕ, применяя методы регуляризации, разложения спектра по базису пробных функций, нейронными сетями и другими методами [1].

В работе представлен метод восстановления спектров нейтронов с применением модели нейронной сети и разработка веб-приложения для хранения, обработки и предоставления результатов расчётов.

1.    Методы и материалы 1.1.    Генерация данных

Для обучения моделей с помощью метода Frascati Unfolding Interactive Tool (FRUIT) [2] сгенерирована обучающая выборка из 10⁵ спектров, полученных как взвешенная сумма четырёхкомпонентных спектров, описываемых моделями деления, испарения, распределения Гаусса и высокоэнергетических нейтронов (см. формула 2). «Эффективные» показания детекторов для набора шаров-замедлителей для каждого спектра были рассчитаны по выражению, приведённому ранее (см. формула 1).

((E) = P th _{V th} (E) + Pe^E + P fv _fE + P_MVM(E)                (2)

где (_th(E) - тепловая компонента Максвелла, (_e(E) - эпитермическая, ( f (E) - быстрая и ( ^i (E) -высокоэнергетический компонента, P_t ^ , P_e , P f , P ^i - доля каждой компоненты в полном спектре (P_th + P_e + P f + P_h i ) = 1. Выражение (см. формула 2) позволяет получить набор спектров моделирующих энергетическое распределение плотности потока нейтронов на большинстве энергетических установок, включая источники деления, радионуклидные источники, медицинские циклотроны и адронные ускорители. Быстрые нейтроны описываются по выражению 3 для модели деления, по выражению 4 - испарения и по выражению 5 для распределения Гаусса (см. формула 3 -5).

Е

(_ff(E) = E ^a e Р

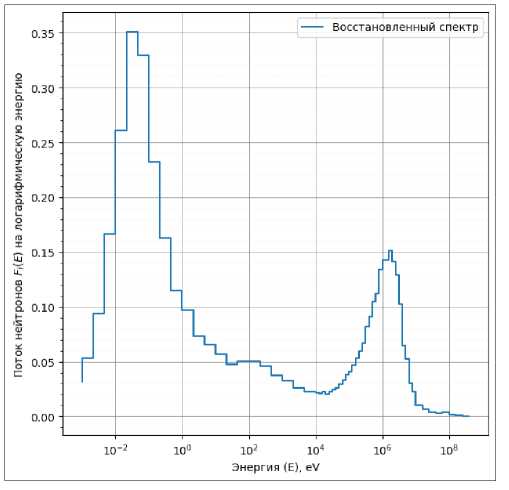
Рис. 1. Сгенерированный спектра № 32

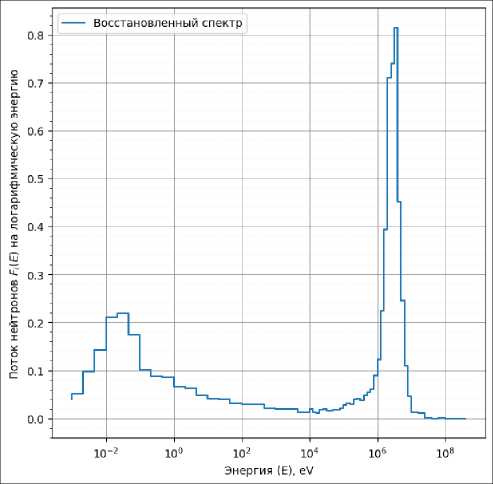
Рис. 2.Сгенерированный спектр № 40

Каждое значение спектра соответствует одному энергетическому уровню. Каждый уровень соответствует значению функции чувствительности, приведённых в сборнике МАГТЭ (см. рис 3) [4]. Интервал их расположения от E_m i _n = 10^-3 эВ до Е_тах = 10⁸ эВ, разделённый на 60 значений.

Для алгоритмов случайного леса и градиентного бустинга 80% обучающей выборки было использовано для обучения, а 20% – для тестирования. Валидация разработанного подхода проведено на базе данных из 340 спектров (251 – из компендиума МАГАТЭ [4], 125 – спектры из статей, решающих подобные задачи) (см. рис. 3) [5 – 8].

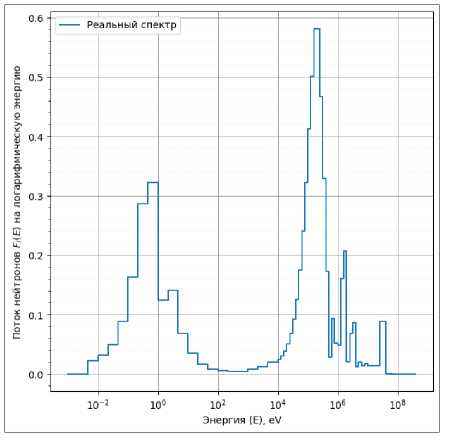
Рис. 3. Пример реального спектра из сборника МАГАТЭ

Тестирование нейронной сети проводилось на базе данных из 340 спектров. 251 спектр был взят из сборника МАГАТЭ. Выборка была расширена путём ручного добавления реальных спектров из других работ [5 – 8].

2.    Модели случайного леса и градиентного бустинга

Для разработанных алгоритмов средствами библиотеки Python Optuna [9] и класса GridSearchCV [10] проведена оптимизация гиперпараметров. Оптимизируемые параметры для случайного леса – число деревьев в лесу; максимальная глубина дерева; минимальное число объектов для расщеплени; ограничение на число объектов в листьях. Оптимизируемые параметры для градиентного бустинга [11] – число решающих деревьев; максимальная глубина дерева; степень расщепления и интенсивность обучения. Лучше себя показал алгоритм случайного леса: Подобранные параметры позволили уменьшить целевой показатель оптимизации: среднюю абсолютную ошибку (МАЕ) на 27%, поэтому далее замеры качества велись для него (см. рис. 4).

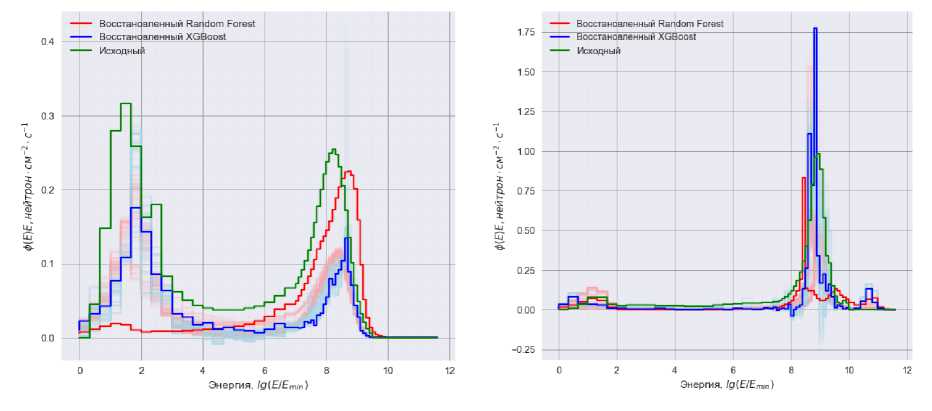
Рис. 4. Результаты восстановления спектров (полупрозрачные области обозначает неопределённость восстановления)

Анализ тестовой и валидационной выборки показал, что восстановленные спектры по своему характеру близки к исходным. В качестве примера на рис. 1 приведено 2 восстановленных графика. Метод позволяет определить положение пиков на графике, а полученный спектр удовлетворяет физическим представлениям. В среднем существует сильная корреляция между исходным и спектром, восстановленным методом случайного леса R = 0,78. МАЕ = 1,63 • 10-2, а среднеквадратичная ошибка (MSE) = 9,02 • 10-4. Неопределённость восстановления спектра была оценено методом Монте-Карло по 103 случайным розыгрышам (см. рис. 5).

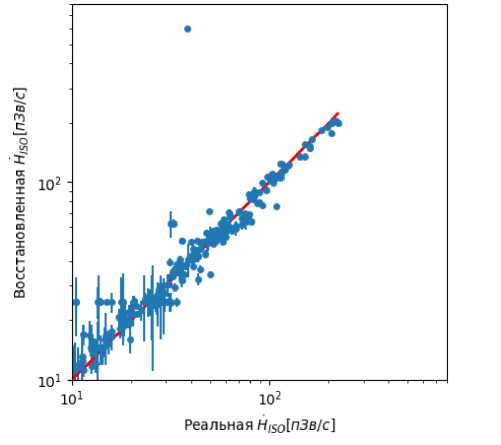
Рис. 5. Сравнение реальной и восстановленной H i _so по тестовой выборке из 376 спектров. Красная прямая - график у = х, вертикальные синие линии - неопределённость восстановления.

Показания детектора были представлены в виде массива случайных чисел, распределённых равномерно в пределах f = 5% от истинного значения. Область неопределённости восстановленного спектра показана на рис. 1 Как видно из рисунка 1, область неопределённости на модели случайного леса узкой полосой повторяет спектр, следовательно, решение достаточно устойчиво к ошибкам измерений. На рисунке 2 приведён график сравнения реальной и восстановленной доз на модели случайного леса по тестовой выборке. Из графика видно, что восстановленные и реальные дозы близки друг к другу за исключением единичного выброса, при котором разница реальная равна 38 пЗв/с, а восстановленная H_iso = 583 пЗв/с, разница между ними ^_iso * ¹⁵⁰0%.

3.    Модель машинного обучения

Разработанная модель машинного обучения представляет собой нейронную сеть с архитектурой, состоящей из 10 полносвязных и 2 Dropout слоями. Каждый полносвязный слой использует функцию активации ReLU , что делает сеть эффективной для решения задач регрессии (см. рис. 6).

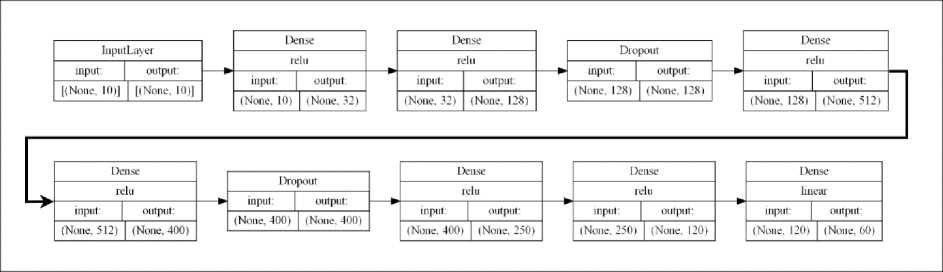
Рис. 6. Архитектура нейронной сети.

На входе в модель подаётся 10 значений Q, полученных на многошаровом спектрометре Боннера. На выходе модель решает задачу регрессии и восстанавливает спектр нейтронов для 60 значений энергетических уровней.

4.    Веб-приложение

Для работы с моделью машинного обучения было разработано веб-приложение на основе фреймворка Streamlit . Для хранения данных используется база данных Postgres . Приложение предусматривает сопровождение процесса дозиметрического контроля и позволяет хранить значения, полученные со спектрометра Боннера, а также спектры, восстановленные при помощи модели нейронной сети. Для расчёта доз загружаются данные расчётов со спектрометра и подаются в модель для восстановления спектра, на его основе рассчитывается эффективная доза [12].

5.    Результаты

Для реализации алгоритма нейронной сети и веб-приложения был выбран язык программирования Python . Для разработки алгоритма модели нейронной сети применялись библиотеки: Scikit-learn для получения информации метрик, Keras и Tensorflow - для сборки, подготовки и настройки параметров модели. Для написания веб-приложения, разработки интерфейса и интеграции модели для проведения расчётов спектров использовалась библиотека Streamlit (см. рис. 7) [12 - 15]. Результат расчёта продемонстрирован на рисунке (см. рис. 8). Мощность дозы по реальному спектру составила 104,33 пЗв • см², по восстановленному - 102,09 пЗв • см². Разница между рассчитанными значениями - 2,19%.

Заполнение данных замера

Рис. 7. Внешний вид веб-приложения.

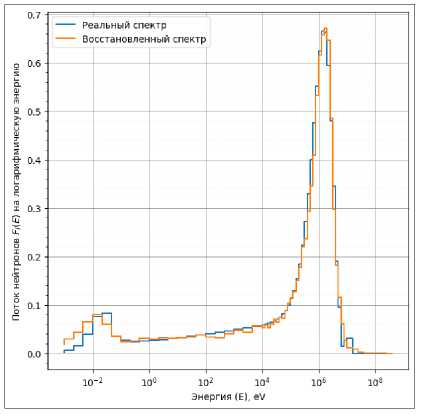
Рис. 8. Восстановленный и реальный спектр № 19.

6.    Дискуссия

Алгоритм нейронной сети на тестовой выборке показал такие значения метрик: R 2 = 0,71, MSE = 3 • 10^-2. Предполагается, что с более корректно сгенерированными аугментированными и расширенным объёмом данных получится повысить точность результатов и позволит сделать шаг в сторону автоматизации обучения модели, так как сейчас модель обучается отдельно.

Также планируется сбор разработанных моделей в ансамбль для повышения качества предсказания.

Веб-приложение позволило упростить работу с моделью, исходными данными и восстановленными спектрами. Планируется расширить функционал для обработки данных другими алгоритмами и статистическими методами, которые позволят проводить комплексный анализ.

Заключение

Был разработаны алгоритмы восстановления спектров нейтронов при помощи нейронной сети и машинного обучения, разработано веб-приложение для взаимодействия с моделью. На тестовых данных алгоритм нейронной сети позволил восстановить спектр с точностью MSE = 3 • 10^-2. Алгоритм случайного леса с точностью MSE = 9,02 х 10^-4. Веб-приложение дополнило функцию модели возможностями для обработки, хранения и предоставления информации в наглядном виде.