Разрешимость краевой задачи для системы обыкновенных дифференциальных уравнений

Рассмотрим периодическую краевую задачу

• ^X 1 ^{( t} ) = f 1 ^{( t}, x 1 (t),X 2 (t),...,X n ( t) ) ,

X n (t) = fn (t, X1 (t),X 2 (t),-*n( t) ), t е [ 0,1] JX1 (0) = X1 (1), X2 (0) = X2 (1)- ■■■, Xn (0) = Xn (1), где функции f1 ,f2,...,fn: [0;1]x Rn ^ R1 удовлетворяют условию Каратеодори.

Краевая задача (1), (2) и ее частные случаи исследовались многими авторами. Известные признаки разрешимости задачи (1), (2) могут содержать так называемые "знаковые" условия на функции ff,—,^ • В данной статье будут получены новые достаточные условия разрешимости задачи (1), (2), в некоторых случаях уточняющие известные в литературе результаты. В работе применены общие утверждения о разрешимости квазилинейного операторного уравнения в резонансном случае.

В некоторых случаях задачу (1), (2) можно рассматривать как периодическую краевую задачу для одного скалярного уравнения. Однако получаемые при этом условия разрешимости не всегда учитывают специфику системы уравнений.

Введем в рассмотрение пространства.

Пусть L 2 = L 2 [ 0;1 ] – пространство суммируемых    с    квадратом    функций

у: [0,1] ^ R1 со стандартной нормой ||»||£^ ; D2) = D2 [0;1] – банахово пространство таких абсолютно     непрерывных     функций x : [0;1] ^ R1, таких, что X е L2 , с нормой II XIId 2 = Iх (0)1 + 1 lXl\l 2;

^L 2 у ^L 2 ^[0;^1] = ^{( У 1, У 2 ,..., У п )/ У ^{е L} 2 , i = 1, ^{n }}

(2) с нормой

II ylLn =1 у1 L 2 +1y 2IL 2 + •••+1 ynL2;

D 2 = D 2 [0;1] = {( х 1, х 2 ,..„X n )/ х ; е D 2 ,i = 1, n } с нормой

II xDn    llX1l D 2 +1X2ID 2 + "• + 1 lXnll-

I D 2.

Определение. Под решением задачи (1), будем понимать совокупность таких n функций, что (X1, X2,.,,, xn ) е Dn [0;1], которые удовлетворяют почти всюду на [0;1] уравнениям (1) и краевым условиям (2).

Обозначим через D n ^,0 пространство:

n, 0 _

^D 2 =

х е Dn [0;1] / хх (0)=                   •

.

. х 1 ⁽ 1 ) ,х 2 ⁽ 0 ) = х 2 ⁽ 1 ) ,

X n ( 0 ) = X n ( 1 )

■■■,

Вспомогательные утверждения.

Теорема 1. Пусть выполнены условия:

• 1)    L - нетеров;

• 2)    F - вполне непрерывен;

• 3)    | FX^ <  a + b\x[\X ;

• 4)    для любого элемента х ₀ е Х ₀ существует такой элемент X i е ker L , что имеет место включение F ( x ₀ + X i ) е imL , причем II ^x il <  Я ^x о| 1 + ^{s ;}

• ⁵⁾    b ⁽¹ +^Y ) <  K I ■

Тогда уравнение Lx = Fx имеет хотя бы одно решение.

Теорема 2. Пусть D - открытое ограниченное множество конечномерного евкли-n дова пространства R , содержащее нуль в качестве внутренней точки. Пусть F(x) - оператор (необязательно монотонный), определенный и непрерывный в замкнутой области D , со значениями в Rn . Если на границе области D скалярное произведение < x, F(x) >> 0, то уравнение F(x) = 0 имеет хотя бы одно решение в D .

Для применения теоремы 1 к задаче (1), (2) предварительно запишем эту задачу в пространстве D n ^,0 в виде операторного уравнения

Lx = Fx ,             (3)

где операторы L : D ^,0 ^ L 2 , F : D n ^ L 2 определены равенствами

( Lx )( t ) = ( x i ( t ), x 2 ( t ),..., X n ( t )) ,

Fx =

' f. (t,Xi (t),x 2 (t),...,xn(t) ),'

f , ^{( t,x} i ^(t),X 2 ⁽t⁾...,X_n⁽t⁾ ) ,..., ’

. fn (t,Xi (t),X 2 (t)..-Xn(t) )

Лемма 1. Ядро и образ оператора n ,02

Операторы P и Q, определяемые ра- венствами

Px = (Xi(0), x2(0),..., Xn (0)),(6)

i                         ii

Q =(yi - j yi(td, y2 - J y2 (td,..., Уп - j Уп (td), 0                00

являются проекторами соответственно на ядро и образ оператора L .

Доказательство. Справедливость равенства (4) проверяется непосредственно.

Проверим справедливость равенства (5). Решим систему xi( t) = yi,

X 2 ( t ) = y 2 ,

,X n ( t ) = Уп для произвольных    yi е L2. Имеем

t xi (t) = j у^ (s)ds + Ci, i = i, n.  Применив пе- риодические краевые условия, получим i                           _____ j yi (t)dt = 0, i = i, n.     По     определению

i

imL = {(yi,y2,...,Уп)еLn / jy(t)dt = 0,i = i,n}.

Справедливость равенства P ² = P проверяется непосредственно.

Для доказательства утверждения (7) достаточно проверить, что оператор C

Q = I — Q, определенный равенством i               i                    i

^QCУ = ⁽ j y i⁽ t ) ^dt , j У 2 ⁽ t ) ^dt ,..., j У п ⁽ td ) , 0         0             0

является проектором. Действительно, Q С (Q с У )= i/i             A i/i             A        i/i             A

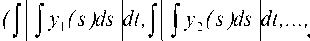
0 <  0            7     0 <  0            7        0 <  0            7

= Q^С у-

Это и означает, что оператор QC является (про- ектором, называемым дополнительным к

Равенство imQ = imL очевидно.

Q .

Лемма доказана.

Определение

Оператор

K p : imL ^ X будем называть обобщенно обратным к оператору L : X ^ Y , ассоциированным с проектором P , если справедливы равенства:

• 1)    LK_p = I , где I : imL ^ Y - естественное вложение;

• 2)    K p Lx = P c x для любого x e X .

Лемма 2. Обобщенно обратный для

оператора      ( Lx )( t ) = ( x 1 ( t ), x 2 ( t ),

...

■, ^x n ⁽ t )) ,

ассоциированный с проектором P (6) имеет вид

В силу леммы 1 существует разложение пространств D^{n ,0}[0,1] и Lⁿ ₂ в прямые суммы:

D n ^,0 = ker L Ф X ₀, L 2 = imL Ф Y ₀ .

Нам потребуются следующие утверждения.

Лемма 3. Для любого элемента x ( t ) e D 2 справедливо неравенство

Ix(t )l -l x (t )l D 2-

Доказательство. Для доказательства утверждения леммы используем представление

t

t

t

K p y = J У 1 ( td J y 2 ( t )dt , ...J У п ⁽ t d

t

x ( t ) = x (0) + J x ( s ) ds .

V 0

и его норма удовлетворяет неравенству

II K P^Dn ^-1.

Доказательство. Непосредственная проверка выполнения условий определения обобщенно обратного оператора показывает, что оператор K является обобщенно обратным к оператору L .

Имеем

LKp у =

Получим

t

I ^x( t) = x^{( 0} ) +J x⁽s)\^ds ^- x^{( 0} ) +1 x⁽ M L = I x⁽ MI D ■

Лемма доказана.

Лемма 4. Пусть существуют неотрица-

тельные постоянные a^a отрицательные функции

,...,

a _n и такие не-

Y 1 ^(t) Y 2 ^(t )>■■■> Y _n(t) , что        Y 1 ( t ), Y 2 ( t ),..., Y n ( t ) e L 2 [0,1] , и

< t

t

t,...,

V 0

V

V о

J y_n ^(t)dt V 0

' 7 7

7' J

(У1 (t),y 2 (t )>■■■> У n(t)).

t

t

t

KpLx = J x^ (s)ds, J x2 (s)ds,...,J xn (s)ds =

V о

(x1 (t) - x1 ( 0 ),x 2 (t) - x 2 (0 ),...xn(t) - xn( 0)) = Pcx.

Найдем оценку K_Py 2 .

II M d 2 =

t

t

+

t

V 0

LP

V о

t

LP

+ ...

Ifl(t,ul,u2,...un) -ai(u 11 + \u22\ +...+\u22

i = 1 ,n ,

для

любых

I^{) +} Y i ^(t)’ t e [0,1] ,

2 1 , u 2 ,...,u_n e R ¹ . Тогда для оператора F справедлива оценка | Fx|_£n - a + b\x\_Dn , где

n

n

а = EMl2, b = Eai.

i = 1                     i = 1

Доказательство.    Действительно, применив утверждение леммы 3, получим II FxLn =1 If.1 IL +1 f 2| Il, + ..-+I К =

n

E i Jl f^(t’^x 1 ^,x 2 ^,...’^x n )^{2 dt}

i = 1

n

-

г t

⁺ J y n^(s)ds

V 0

n

-EifMuJ+u 2I

i = 1

+ ... + u 2 1^{)+ Y} i ⁽t)

dt >

t

LP

= 1W L ₂ ⁺l| y 2 1 L ₂ ⁺ ... + 1 M l 2 =| \у\\_ь« .

Лемма доказана.

-E («Mn + Ml )-a + bllxM i=1

Лемма доказана.

Для произвольно фиксированного элемента ( x 1 , x₂,—,x_n ) e D n ^,0 определим непрерывное отображение Ф : R ⁿ ^ R ⁿ равенством

Лемма 5. Если выполнены условия

• 1)    существуют неотрицательные постоянные « [ , « 2 ,..., a n и такие неотрицательные функции         / 1 ( t ), / 2 ( t ),..., Y n ( t ) ,        что

• Y1(t) Y2(t),..., Yn (t) e L2[0,1]                    и
• If(t,иъu^...Un) < ai(u1| + \u2I +...+\u2I)+Yi(t)

i = 1 ,n ,      для      любых        t e [0,1] ,

• > ^c(u 1| ⁺ \u ₂| ⁺ ... ⁺ \u_n\)² - ^ ^(t),

тогда для отображения Ф : Rn ^ Rn сущест-0 х^0

Ф(С10, С20,...С0) = (0,0,...0), причем     С0! + С0| +... + С0| < r,где

~  ~\~

r = 1 1 +--I x n_n +---+ 1 , a = max a ,

<       c   J" "D2    c

~ = max vrai max I Y i ( t )|, &  = vrai max & ( t )|. i      t e [0,1]                          t e [0,1]

Доказательство. Для того чтобы по казать, что на выпуклом множестве

B ( r ) = {( C 1 , C 2 ,..., C n )/ C 1 + С ₂ + ... + C n <  r } ,

Ii a + y in и        &   .

где r = 1 1 +--I x n +---+ 1 , условия

[     c J "D2   c теоремы 2 выполнены, достаточно оценить скалярное произведение

<Ф(C1,С2,...,Cn),(C1,C2,...,Cn) > для произвольных (C1,C2,..., Cn) e dB(r).

Теорема 3. Пусть выполнены следующие условия:

• 1)    существуют неотрицательные постоянные a 1 , a 2 ,..., a n и такие неотрицательные функции         Y 1 ( t ), Y 2 ( t ),..., Y n ( t ) ,        что

• Y1(t),Y2(tX-, Yn(t) e L2[0,1]                   и
• |fi(t,ubu2,...,un) < ai(uJ + u2I + — + u2|)+ Yi(t)

^{+ u} n ^f n ^(t,u 1 ^,u 2 ^..V n ) >

^c(|^u 1| ⁺ \^u 2I ⁺ ... ⁺ | ^un|)² - &^(t);

• 3)    выполнено условие ( ' 1 + a 2 + ... + a n )(1 + y ) <  1 ,

i a + Y где y = 1 +-- .

c

Тогда задача (1), (2) имеет хотя бы одно решение в пространстве D n [ 0;1 ] .

Доказательство. Справедливость первых двух утверждений теоремы 1 очевидны. Условие 3 теоремы 1 выполнено в силу леммы 4.

Лемма 5 гарантирует существование та кого элемента ядра и , что имеет место вклю- чение

F ( x 0 + и ) e imL . Оценим норму

¹ Dn .

I u |I d n

I C ,| I l, +1 | C 21 L + ... + I | C,||

.  <

^L 2

' 2

~~

<| 1 ⁺ 'R )K n

~

+ &  + 1 .

c

Выполнение условия 5 теоремы 1 автоматически следует из условия 3 теоремы и леммы 4. Теорема доказана.