Разрешимость нестационарной задачи теории фильтрации

Пусть множество J — промежуток в R, содержащий нуль, и Q С R n - ограниченная область с границей dQ класса C “ . В цилиндре Q х J рассмотрим задачу Коши-Дирихле

u(x, 0) = u g (x),          x G Q,

u(x, t) = 0,

(x, t) G dQ х J

для уравнения

(A - A)u t (x,

n _{∂           ∂}

t) = ъ dx (m ij (x’*> j

u(x, t) + g(x, t),

(x, t) G Q х J,

где вещественные функции m ij (x, t), удовлетворяющие условию m ij (x, t) = m ji (x, t), а также параметр A G R + характеризуют свойства среды, однако в [1] было отмечено, что отрицательные значения параметра λ не противоречат физическому смыслу. Подобный вид имеют многие уравнения теории фильтрации [2 – 4]. У этих авторов изначально, вообще говоря, нестационарная задача заменяется на стационарную, то есть m ij (x,t) = m ij (x). Целью же данной работы является найти решение задачи, приведенной выше, при условии зависимости коэффициентов от времени.

Для построения решения поставленной задачи исследуем сначала абстрактную задачу для нестационарного операторно-диференциального уравнения.

Пусть U и F — банаховы пространства, операторы L, M t G L (U; F) (т.е. линейны и непрерывны) при каждом t G J. Рассмотрим в банаховых пространствах линейные уравнения

LU(t = M t u(t),

Lu(t) = M t u(t) + g(t)

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ с функцией g : J ^ F, неразрешенные относительно производной по времени. Такие уравнения часто называют уравнениями соболевского типа ( см. [3, 5, 6]), которые в последнее время нашли применение в задачах измерения динамически искаженных сигналов [7, 8].

Если оператор L — непрерывно обратим, то уравнения (4), (5) сведутся к разрешенным относительно производной уравнениям вида

v(t) = A t v(t),      v(t) = A t v(t) + h(t).                               (6)

Такие уравнения с ограниченнным оператором A t , t ∈ J, и задача Коши для них, подробно рассмотрены в монографии Ю.Л. Далецкого и М.Г. Крейна [9]. Среди работ, в которых исследовались уравнения такого вида с неограниченными операторными коэффициентами, отметим работы Т. Като [10], О.А. Ладыженской и М.И. Вишика [11], К. Иосиды [12], С.Г. Крейна [13], Д. Хенри [14].

Разрешимость одного класса уравнений соболевского типа (4), (5) с неограниченными операторными коэффициентами изучена в работе А. Фавини и А. Яги [15].

При рассмотрении вопросов разрешимости уравнений (4), (5) и задачи Коши

u(t o ) = u o                                               (7)

для них при t 0 ∈ J в предположении нетривиальности ядра оператора L , как и в работах [5, 6] для стационарных уравнений соболевского типа, будет использовано условие ограниченности L -спектра оператора M _t и, как следствие, возможность построения некоторых проекторов на пространствах U и F. В результате исходное уравнение будет редуцировано к системе двух уравнений на взаимно дополнительных подпространствах. Одно из этих уравнений примет вид (6) с ограниченными операторами A _t , поэтому в целом результаты настоящей работы можно считать обобщением соответствующих результатов [9] на случай необратимого оператора L .

1.    Относительно спектрально ограниченная оператор-функция

Пусть U и F — банаховы пространства, J — промежуток в R, операторы L E L (U; F), M t E L (U; F) для всех t E J.

Следуя терминологии, используемой в [5, 6], множества p ^L (M _t ) = { /../ E C : (^L — M t ) ^{- 1} E L (F;U) } и a ^L (M _t ) = C \ p ^L (M _t ) будем называть соответственно ^-резольвентным множеством и L - спектром оператор-функции M _t .

Очевидно, что если ker L П ker M t = { 0 } при некотором t E J, то p ^L (M t ) = 0 .

Лемма 1. [5] Пусть операторы L E L (U; F), M t E L (U; F) для t E J. Тогда L-резольвентное множество p ^L (M t ) оператора M t открыто , а L-спектр a ^L (M _t ) оператора M t замкнут.

При t E J оператор-функции комплексного переменного (^L — M t ) ^{- 1} , R^M t ) = (^L — M _t ) ^{- 1} L, L ^ (M t ) = L(^L — M t ) ^{- 1} с областью определения p ^L (M t ) будем называть соответственно L-резольвентой, правой и левой L-резольвентами оператора M _t .

В дальнейшем будут использоваться тождества, справедливые при фиксированном t ∈ J и любых ^, A E p ^L (M ):

(А — ^)(AL — M t ) ^{- 1} L(^L — M t ) ^{- 1} = (^L — M t ) ^{- 1} — (AL — M t ) ^{- 1} , L(^L — M _t ) ^{- 1} M _t = M t (^L — M ) ^{- 1} L.

Лемма 2. Пусть операторы L E L (U;F), M t E L (U;F) для t E J. Тогда L-резольвента, правая и левая L-резольвенты оператора M t аналитичны по ^ в p ^L (M _t ) .

Определение 1. Оператор-функция M t называется спектрально ограниченной относи тельно оператора L (или просто (L, ст)-ограниченной), если

B a t Е C (J;R + ) V t Е J тах {| ц | : ц Е CT ^L (M _t ) } <  a t < + го .

Лемма 3. Пусть оператор-функция M t Е C (J; L (U; F)) (L, ст) - ограничена. Тогда при ц Е E _t = { А Е C : | А | >  2a _t } оператор-функция (цL — M t ) ^{- 1} Е C (J; L (F;U)).

Доказательство. Возьмем 6 >  0, чтобы при | т — t | <5 выполнялось a _T <  2a _t . Тогда при таких т Е J получим E t С p ^L (M _t ) n p ^L (M _T ). В силу справедливости равенства (цL — M _т )(цL — M t ) ^-1 = I + (M t — M t )(цL — M t ) ^{- 1} при \W t — M t ||l(U;F) <  \ (цL — M t ) ^-1 ^ ^-^ ) получим

(цL — Mt>L — Mt)-1 = 2 ((Mt — Mt)(цL — Mt)-1)k , k=0

(цL — M t ) ^{- 1} — (цL — M t ) ^{- 1} = (цL — M t ) ^{- 1} 52 ( (M t — M t )(цL — M t ) ^{- 1} ) k .      (9)

k =1

Следовательно, | (цL — M_t ) ^{- 1} — (цL — M _t ) ^{- 1} ||-(f _; u) ^ 0 при т ^ t. Причем этот предел равномерен по ц Е Y С E t , где y — замкнутый контур. Действительно, возьмем \ M_t — M t \- ( U ; F ) <  2 CC 2 , где C = mаx {| (цL — M t ) ^{- 1} \- ( F ; U ) , ц Е y } , тогда сразу для всех ц Е Y

II ^^{L — M} t ^{) - 1 — (}Ц^{L — M} t ^{) - 1}\ - ( F ; U ) <  2 _{— £} /с < ^£.

Теорема 1. Пусть оператор-функция M _t Е C (J; L (U; F)) сильно дифференцируема по t Е J и (L, ст) -ограничена. Тогда оператор-функция (цL — M _t ) ^{- 1} сильно дифференцируема по t Е J при ц Е E t = { А Е C : | А | >  2a _t } .

Доказательство. Возьмем ц Е E t , f Е F, 6 >  0. Выберем т как в предыдущем доказательстве. Пусть u _t = (цL — M _t ) ^{- 1} f, тогда получим, используя (9),

(цL - M T^f) ЦL - M _i ) 2 ¹ f — ^цL _ M t ) - 1 dM ^цL _ _Mlrt =

Т t                                dt

(цL — M t ) ^{- 1}

/ Mt — M t

У ^{т —} t

52 ((цL — Mt)-1 (Mt k=1

— M t )) k ^{- 1}

—

dM t dt

(цL — M t ) ^{- 1} f

U

(цL — M t ) ^{- 1}

(

Mt — Mt ut т — t

—

dM t

—ET ut ⁺ dt

M t — M t

т —

t

∞ k=1

((цL — M t ) ^{- 1} (M t — M t )) k u t

<

U

T -1||      ( Mt — M t     dM t

< ^ ^{(цL — M t )}    || - (f , u) т — t ^{u t —}

+

F

+

M t —

т —

M t t

∞

52 ^ (цL — M t)-Ч M т — M t ) ^ L (u) \( цL — M t ) ^{- 1} f \ u . l (U;F) k =1                                                        /

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Покажем, что это выражение при т ^ t стремится к нулю равномерно по ^ G y С E t , где γ – замкнутый контур. Действительно, так как контур компактен, последнее выражение достигает максимума при некотором ^ q G 7. В силу леммы 3 и принципа равномерной ограниченности его можно оценить сверху равномерно по µ ∈ γ следующим выражением

|| ⁽№L - M t ) ¹

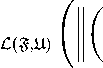
M τ - M t τ - t

- dM) (_№l - M t ) ^{- 1} f

+

F

+C2 ||(WL - Mt)-1 (Mt k=1

-

M t ) !^ ^ (^ q L - M t ) ^{- 1} f Hu) ,

которое стремится к нулю при τ → t. Следовательно,

V f G F -d ((^L - M t ) ^{- 1} f) = (^L - M t ) ^{- 1} dM t (^L - M t ) ^{- 1} f.           (10)

dt                                     dt

□

Пусть оператор-функция M t (L, а)-ограничен, а контур Y t = { ^ G C: | ^ | = 2a _t } . Рассмотрим интегралы

P t = 1^ [ R ^L L (M t) d^,    Q t = -^ [ L ^L L (M t) d^,

2ni J p                   2пг J p

γt                                      γt которые существуют в силу леммы 2. В [5] показано, что при фиксированном t ∈ J операторы Pt : U ^ U и Qt : F ^ F являются проекторами.

Лемма 4. Пусть оператор-функция M _t G C (J; L (U; F)) сильно дифференцируема по t G J и (L, a) -ограничена. Тогда оператор-функции P _t G C (J; L (U)) и Q t G C (J; L (F)) сильно дифференцируемы по t ∈ J.

Доказательство. Возьмем 6 >  0 так, чтобы при | t - т | <  6 выполнялось a _T < 2a _t , получим

P t u - P t u = —Ц [ R L (M T )ud^ - 2ni J ^

γ τ

2П У R L (M t )ud^ ₂ У ( r L (M t )u - R L (M t )u) d^.

γ t

γ t

Из доказательства леммы 3 следует равномерная непрерывность P _t . Далее получим

P _τ u - P _t u τ - t

^-     /⁽^^{L -} M t ) ¹ ~TT^R L ^(M t ^)ud^ <

2ni J                dt ^

^{Y t}                                     U

<

- 2nj

γ t

R ^L L (M t )u - R L (M t )u τ - t

- (^L - M t ) ^{- 1} dMR L (M t )u

| dµ | ,

U

откуда из (10) с учетом равномерной сходимости на γ t разностного отношения к производной следует сильная дифференцируемость P _t и

∀ u ∈ U

-dP t u = ^ /(^L - M t ) ^{- 1} dM t R ^L L (M t )ud^. dt        2П i J                  dt

γ t

Сильная дифференцируемость Q _t показывается аналогично.

Положим U 0 = ker P t , F 0 = ker Q t ; U 1 = imP t , F ¹ = imQ t для всех t E J. Обозначим через L _t,k , M _t,k сужение операторов L, M _t на U ^k , k = 0,1.

Теорема 2. Пусть оператор-функция M t E C (J; L (U; F)) (L, ст)-ограничена. Тогда

• (i)    имеет место действие операторов L _t,k : U k ^ F k , M _t,k : U ^k ^ F k V t E J, k = 0,1;

• (ii)    существуют операторы M — E L (F 0 ;U 0 ), t E J, причем, если оператор-функция M t : J ^ L (U; F) сильно дифференцируема, то оператор-функция M _tg^L (I — Q _t ) E L (F;U 0 ) сильно дифференцируема по t ∈ J, а при условии сильной непрерывности оператор-функции dd M t оператор-функция dd (M t - ¹ (I — Q _t )) также является сильно непрерывной по t E J;

• (iii)    существуют операторы L ^{- 1} E L (Ft; Ц"), t E J, причем оператор-функция L — Q t E C (J; L (F; U j ).

Доказательство. Первое утверждение из (i) имеет место в силу соотношения LP _t = Q _t L, которое вытекает из очевидного тождества LR L (M _t ) = L L (M t )L. Второе утверждение справедливо в силу соотношения M _t P _t u = Q t M t u, которое вытекает из тождества (8).

• (ii)    Пусть f ⁰ ∈ F _t ⁰ , тогда

M ty^ [⁽^^{L —} Mt) ^1f 0 — = ., . [ ~f 0 ⁺    ■ [ ^LL^(Mt^)f 0dV = ^{— f} 0 -

2пг J                 ц 2ni J ц 2ni J ^

γ t                                        γ t                    γ t

Если u ⁰ ∈ U _t ⁰ , то

A^L — M t ) ¹ d^M t u ⁰ = —    [ ~u ⁰ +     [ R L (M t )u°d^ = — u°.

2ni J              ^            2ni J ^       2ni J ^

γ t                                             γ t                    γ t

(Все равенства здесь получаются из (8) при А = 0). Значит, оператор Mt. 0 равен сужению на F _t ⁰ оператора

— — / (^L — Mt)-1 — -

2ni J^

γ t

Найдем производную оператор-функции

Mм^(1 — Qt) = —/(^L — Mt) 1 ~(I — Qt), '                2ni J^

γt которая, если существует, имеет вид

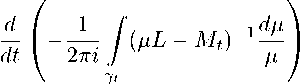
( I — Q t ) +

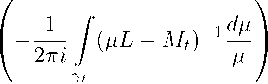
d(I — Q t ) dt

Сильная дифференцируемость проектора (I — Q _t ) следует из леммы 4. Сильная дифференцируемость оператора (11) доказывается так же, как сильная дифференцируемость проекторов в лемме 4.

Покажем, что при условии сильной непрерывности оператор-функции _d ^d _t M _t сильно непрерывен по t ∈ J интеграл

— -¹, /"(^L — M t ) ^{- 1} dM t (^L — M t ) ^{- 1} d^.

2кг J               dt              ц

γ t

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

При | t — т | <  5 обозначим u _T^ = (^L — М _т ) f , тогда

1 Л _т dM-idMt d^ Г _MV1dM_T d^

IУ -L - ^Mt) ^г"** 7 - У ' - M T > -s-t- 7 γ t                                     γ τ

<

U

< 2л/ 1 ^<(^^L γ t

— M t ) ^{- 1}

— (^L — M t ) ^{- 1} ) dM * u t, + (^L — M t ) ^{- 1} d^ dt                         dt

—

dM τ dτ   ^{u t,µ}

Ж

U Ы +

+2n

/ ⁽^^{L —} M T )

dM τ

dτ

⁽u t,^

—

^и т,ц )

γ t

^{| d}^ | <  u

< sup || (^L — M t ) ¹ — µ ∈ γ t

⁽^^{L —} M T ) ^LF.U sup

µ ∈ γ t

⁺ sup || ⁽^^{L —} M T ) ^LF. U ^suP µ ∈ γ t                            µ ∈ γ t

dM t dt ^{u t,µ}

+

F

/ dM _t dM_T\ dt dτ

^u t,µ

^{+ su}P ^{| (}^^{L —} M T ) 1l^ µ ∈ γ t

dM τ dτ

L ( U ; F ) ^ ^ Y t

+

F sup ||ut,^

иЖ1я <

<

dMt dt ut,µ0

^sup |^|(^^{L —} M t ) ^{1 —} (ML — M T ) ¹ |^| L ( F ; u ) ⁺

F л" '■                                                                  ^{v ; 7}

+

dM t   dM τ

"dt      dT" ) ^Ut’^M0

sup sup ||(^L — M t ) ^LF . U +

F | t τ | <δ µ ∈ γ t

+ C sup sup ||(^L — MT) 1 ^(F.U) sup ||ut,^ — uT,^ ||U ^ 0 |t τ|<δµ∈γt                               µ∈γt при т ^ t. Здесь использованы лемма 3, компактность контура y* и принцип равномерной ограниченности.

Cильная непрерывность оператор-функции dt (I — Q _t ) доказывается аналогично.

• (iii)    Согласно лемме 4 оператор L t 1 равен сужению на F ¹ оператора

  — [ (^L 2ni J

  
  

  — Mt;¹) ¹dp,.

  
  

γ t

Отсюда следует непрерывность в смысле операторной нормы в L (F) оператор-функции L-^Q t по t G J.                                                                          □

Замечание 1. Нетрудно показать, что в предположении F ¹ = F ¹ оператор-функция L t 1 G C (J; L (F ¹ ; U1 )).

При условии (L, ^-ограниченности оператор-функции M _t в условиях теоремы 2 имеем операторы H _t = MtoL _t, o G L (U 0 ) и S _t = Lt^M _t, 1 G L(Ut ), используя которые можно разложить L-резольвенту оператора M _t в кольце | ^ | >  a _t в ряд Лорана

∞∞

(^L — M t ) ^{- 1} = ^ц^кH k М*-_о\1 - Q t ) + ^Ц ^- k S - ¹ L t, 1¹ Q t .

k =0                        k =1

Определение 2. Бесконечно удаленную точку назовем устранимой особой точкой, полюсом порядка p ∈ N или существенно особой точкой L-резольвенты оператор-функции M _t , t E J, если соответственно V t E J H _t = O; 3 t o 6 J H^ = O,   H i' + = O; H _t q = O V q 6 N.

Определение 3. (L, ст)-ограниченную оператор-функцию M t будем называть:

• (i)    (L, 0)-ограниченной, если бесконечность является устранимой особой точкой L-резольвенты оператор-функции Mt ;

• (ii)    (L,p)-ограниченной, если бесконечность является полюсом порядка p E N L-резольвенты оператор-функции M_t ;

• (iii)    (L, го)-ограниченной, если бесконечность является существенно особой точкой L-резольвенты оператор-функции M_t .

2.    Существование решений

Теорема 3. Пусть оператор-функция M t E L (U; F) (L, 0)-ограничена. Тогда ker L = U 0 , imL = F ¹ для всех t E J.

Доказательство см. в [5].

В дальнейшем будем обозначать ker L = ker P t = U ⁰ , ker Q _t = F 0 ; imP _t = U 1 , imL = imQ _t = F ¹ ; через L o обзначим сужение оператора L на U ⁰ , L _t , 1 - сужение оператора L на U 1 ; M _t,k , k = 0,1, есть сужение операторов M t на U ⁰ и U соответственно, t E J.

Решением уравнения (4) будем называть вектор-функцию u E C ¹ (J; U), удовлетворяющую этому уравнению на J.

Определение 4. Семейство множеств {P t С U : t E J } назовем обобщенным фазовым пространством уравнения (4), если

• (i)    для любого решения u(t) уравнения (4) для любого t E J выполняется u(t) E P t ;

• (ii)    для любого u 0 ∈ P t ₀ , существует единственное решение задачи (7), (4).

Теорема 4. Пусть t E J, оператор-функция M t E C (J; L (U; F)) (L, 0) - ограничена. Тогда обобщенным фазовым пространством уравнения (4) является семейство множеств { L-^F ¹ ]: t E J } .

Доказательство. Построим решение уравнения (4). Подействуем на уравнение проектором (I — Q t ) и получим

^{(I — Q} t ^)Lu(t) = ^{(I — Q} t ^)M t u^(t)

для всех t E J, поскольку ker(I — Q t ) = imL, то

0 = Mt(I — Pt)u(t) = Mt,ouo(t), и в силу обратимости оператора Mt,0 (см. теорему 2) имеем u0 (t) = (I — Pt>(t) = 0.

Теперь сделаем замену Lu(t) = f (t) E F1 для всех t E J в уравнении (4). Представим u(t) в виде u(t) = u0(t) + Ptu(t), тогда f (t) = Lu(t) = Lu0(t) + LPtu(t) = 0 + LPtu(t) = Ltj1Ptu(t).

Так как в силу теоремы 2 оператор L _t, 1 непрерывно обратим и P t u(t) = L - f (t), то, следовательно, уравнение (4) на подпространстве F ¹ примет вид

Lu(t) = LUT = f(t) = M t u(t) = M t u ⁰ (t) + M t P t u(t) = 0 + M t L —1 f (t).

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Получили уравнение

f(') = M t L - f (t),                                  (12)

с оператор-функцией T _t = M _t, i L -1 E C (J; L (F 1 )) (см. замечание 1). Решение задачи Коши f (' o ) = f o E F ¹ для уравнения (12) согласно [9, с.138-153] имеет вид f (t) = F (t)f o , где оператор F (t) E L (F 1 ) при t, t o E J задается следующим образом

t

^F(t) = IF^{1 +}

j Tti dti + t0

tt

t 2

∞

ум

n =

n

t 0 t 0

t 0

T t n T t

n

T t ₁ dt 1     dt n

и называется оператором Коши уравнения (12).

Решение уравнения (4) имеет вид u(t) = L -1 F (t)f o , и каждому u o E { L—^F ¹ ] : t E J } соответствует f o = Lu o E F ¹ , для которого решение единственно. Следовательно, семейство { L—^F ¹ ] : t E J } является обобщенным фазовым пространством. □

3.    Неоднородное уравнение

Дальнейшие рассуждения проведем в предположении (L, 0)-ограниченности оператор-функции M t E C (U; F).

Определение 5. Оператор U(t,T ) = L - F (t)F ^{- 1} (т)L _T , 1P _T назовем эволюционным ( разрешающим ) оператором уравнения (4).

Лемма 5. Эволюционный оператор U(t,T ) обладает следующими фундаментальными свойствами:

• (i)    U (t,t) = P t ;

• ⁽ⁱⁱ⁾    U^(t,s)U^(s,T) = U^(t,T);    1

• ^{(iii)    U(}',^т) 1 и т = [U^:;-') u. It ;

  ^{( t} <  ')•

  
  

• ^(iv)    ll^U(t,T ^Il^) <  K^exP (7 H ^T s H L ( F 1 ) ^dS)

Доказательство очевидным обазом следует из вида эволюционного оператора.

Теорема 5. Пусть оператор-функция Mt E C(J; L(U; F)) сильно дифференцируема по t E J, (L, 0)-ограничена и вектор-функция g E C 1(J, F). Тогда для любого начального значения uo EGto = {uEU:(I — Pto)u = — Mt0 1o(I — Qto)g('o)} существует единственное решение u E C1 (J, U) задачи (7) для уравнения (5), причем

u ( t ) =

t

U (t,to)uo + У t0

U (t,T)L_T 1 1 Q t д(т )dT

- M _t ^- _o ¹ ( I - Q t ) g ( t ) .

Доказательство. Подействуем проектором (I — Q _t ) на уравнение (5), получим

⁽I ^{— Q} t ^)Liu^(t) = ⁽I ^{— Q} t ^)M t u^{(t) + (I — Q} t ^)g(t)i L(I — P t )ii(t) = M t (I — P t )u(t) + (I — Q t )g('), о = (I — P t )u(t) + M _t~₀4 i — Q t )g(t).

Как и прежде, обозначим u0(t) = (I — Pt)u(t), тогда uo(t) = —M-1(I — Qt)g(t).

Вновь сделаем замену Lu(t) = f (t) G F ¹ для всех t G J и получим

(LU(t)) = f (t) = M t u(t) + g(t) = M t u°(t) + M t P t u(t) + g(t) =

= M t ^{( — M} t. p ⁽I - ^Q t )g^{(t)) +} M t ^p t u^{(t) +} g^(t) = ^{— (}I - Q tW ) ⁺ M t ^p t u^{(t) +} g^(t) =

= M t P t u(t) + Q t g(t) = M t L^f (t) + Q t g(t).

Таким образом, уравнение (5) мы можем представить в виде системы двух уравнений f (t) = Ttf (t)+ Q^t),                                (14)

0 = u°(t) + M^I — Q t )g(t)                            (15)

на подпространствах F1 и U0 соответственно. Решение задачи Коши f (to) = fo G F1 для уравнения (14) согласно [9, с.138-153] имеет вид t г f (t) = F(t)F 1 (to)fo + j F(t)F 1 (t)Qtд(т)dT. t0

Из приведенных выше рассуждений следуют равенства P t u(t) = L t 1 f (t) и f o = L _{t 0 ,} 1 P _{t 0} u 0 , а, следовательно,

t

P t u(t) = l^f (t)F - ¹ (t o )L t o , 1 P t o u o +

j L t, 1 F(t)F 1 (т '^^Qt д(т)dT.

t 0

Функция u°(t) = — M t 0 (I — Q t )g(t) является непрерывно дифференцируемой в силу теоремы 2 (ii) и разрешает уравнение (15). Следовательно, (13) является решением задачи (7), (5).

4.    Решения нестационарной задачи теории фильтрации О Редуцируем задачу (1)-(3) к задаче (7), (5), для этого возьмем пространства U =Н 1(Q), F = H- 1(Q) и обозначим через Ao оператор Лапласа А, действующий из U в F. Пусть функция g G C 1(J;F), {Ak : k G N} - собственные значения оператора Ao, занумерованные по невозрастанию с учетом их кратности, {фк(x) : k G N} - множество соответствующих собственных функций. Будем предполагать, что A G a(Ao). Обозначим собственные вектора, соответствующие A, через ^i(x), l = 1,r, где r - кратность A в спектре a(Ao). Зададим операторы L = A n∂           ∂ А,м-=:Е1 ^ (mj (x-t) dx") GL(U; F), t G J.

Лемма 6. Пусть функции m ij (x,t) G C 1 (J; L ^ (Q)), тогда оператор-функция M t : J ^ О

L (H ¹ (Q); H - 1 (Q)) непрерывно дифференцируема по операторной норме.

Доказательство. Через (w,v) обозначим действие функционала w G H-1 (Q) на вектор О v GH1 (Q). Введем обозначения 8Mt0 = Mt — Mt0, Smij = mij(x,t) — mij(x,to), = {5mij}П"=1, ^5Mt01| - норма матрицы.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Имеем 6M t 0 u =

A dXi Ь j i,j = 1                     J

поэтому

n

K^M t o u^-v) | = E / j ¹ Q

n

Q

∂u ∂v

δm ij        dx

∂x j ∂x i

= У (бМ t ₀ V u, V v) R n dx <

Q

J | (SM „ ^V u, \    . | dx <  C«.up ИЙ ^ ,

Q

.

Получили, что ||5M t₀ u | _H । (q) <  Cess sup ||tM t₀ ||H u H °    , а значит, при m ij E C ¹ (J; L ^ (^))

0                   x e Q 0      h ¹ (q)

• и | t — t o | <  6 верно следующее неравенство ||5Mt₀ 1|    °             <  Cess sup ||^Mt₀ 1| <  E.

L( H 1 (Q); H ^{- 1} (Q))         x _G q

Поскольку

следующее

δM t 0

5t

dM t 0 dt

< C ess sup

L ( H 1 (Q); H ^{- 1} (Q))        x ^{G Q}

°            <  C ess sup

L( H 1 (Q); H ^{- 1} (Q))         x EQ

Теорема 6. Пусть матричная функция M t

δM t 0

5t

∂M t 0 ∂t

, то при t — t o = St ^ 0 получим

9M t₀   J dm ij     )

- ^где “аГ = t д

n

□

i,j =1

\T         t\^l^ ^d^ k

^J_q m j ^(x,t) dx ₃ Эх _г

dx

r

при всех

k,l =1

t E J такова, что det M t = 0. Тогда для любого t E J оператор-функция M t (L, 0)-

ограничена.

Доказательство. Пусть A E a(Ao), тогда любой ненулевой вектор ^ из ядра оператора L r можно представить в

виде ^ = У^ a i ^ i . Возьмем вектор b = (a 1 ,... -a _y ) E R ^r

, тогда

l =1

n∂             ∂rr

^ dx (mij(x,t)IxT^ai^i(x) ) ^akVk(x)dx = q i,j=1    i X              j l=1

rrn

= — E aiE aij (x-t) Ц¹   dx = (Mtb- b)^ =0 (16)

i=1 k=1 i,j=1 Q для всех ненулевых векторов b E Rr в силу условий теоремы. Поскольку оператор L самосопряжен в L2(Q), то образ imL ортогонален ядру ker L в смысле L2(^). Поэтому из (16) следует, что Mt^ / imL. Следовательно, оператор L не имеет Mt-присоединенных векторов. Поскольку оператор L фредгольмов, из теоремы 4.6.1 [6] следует требуемое.

В силу леммы 6 и теоремы 6 справедлива теорема 5 о разрешимости задачи (1) – (3).

В заключение хочу выразить благодарность Г.А. Свиридюку за постановку задачи и интерес, проявленный к данной работе, а также В.Е. Федорову за полезные советы и констуктивную критику полученных результатов.