Разрушение релаксационных колебаний в новой модели экстремальной динамики численности популяции
Автор: Переварюха Андрей Юрьевич
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Компьютерное моделирование
Статья в выпуске: 1 (38), 2017 года.
Бесплатный доступ
В контексте моделирования нетривиальных перемен в развитии популяционных процессов предлагается уравнение с запаздыванием 𝑥˙ = 𝑥(𝑡)𝑓(𝑥(𝑡- )) (𝑥(𝑡- )), где, > 0, (𝑥) - меняющая знак функция. В новой модели трактовка предпороговой емкости среды отличается от асимптотического балансового равновесия 𝑥(𝑡) → из уравнения Ферхюльста - Пирла. Вычислительное исследование потери устойчивости особой точки показывает помимо известного сценария образования глобального орбитально устойчивого цикла в логистическом уравнении с запаздыванием другой вариант метаморфоза - с разрушением возникших при изменении репродуктивного параметра неустановившихся релаксационных колебаний и появлением неограниченного сверху псевдопериодического решения. При возрастании амплитуды релаксационных колебаний сценарий катастрофического завершения фазы роста численности популяции реализуется в зависимости не от достижения критического минимума, а от положения максимума в случае превышения нестабильной популяцией допустимой поддерживающей емкости среды. Модель применима для описания вспышек численности ряда биологических видов, сильно воздействующих на пригодность среды своего размножения.
Модели популяционных колебаний, уравнения с запаздыванием, регулярные циклы и вспышки численности, редкие экологические сценарии, пороговые ситуации
Короткий адрес: https://sciup.org/14968886
IDR: 14968886 | УДК: 517.929,519.1 | DOI: 10.15688/jvolsu1.2017.1.6
Текст научной статьи Разрушение релаксационных колебаний в новой модели экстремальной динамики численности популяции
DOI:
Дифференциальные уравнения с запаздыванием вызывают интерес в естественных науках, так как поддерживают теоретическое математическое объяснение для сценариев возникновения длительных колебательных режимов, когда внешние периодические воздействия исключены условиями экспериментов.
Несколько известных в системной экологии моделей предложены как дополнения уравнения экспоненциального роста ж = Лж в попытках формализовать саморегуляцию численности: ж = Лж • /(ж ^ ), ^ > 0. Дополнения призваны отражать наиболее общие ситуации, когда конкурентные факторы в некоторый момент начинают тормозить скорость роста популяций. Первым описанием ограниченного роста стала модель «логистического роста»:
d-N = rN fi - N), dt к ,
(1’)
N (t) =
N (0)ert
1 + N (0)(ert — 1)/K'
Асимптотика решения уравнения (1) для V N(0) > 0 подразумевала плавный выход численности популяции к стационарному состоянию K , соответствующему балансу со средой. Кривая (1’) не рассматривалась П. Ферхюльстом как единственно возможная для модели ограниченного роста [2]. Далеко не всегда наблюдалось замедление темпов прироста населения, которое для (1) должно происходить после N > K/2. В ряде альтернативных модификаций логистической модели варьируется именно положение точки кривой, где /"(N) = 0.
В правую часть (1) можно добавить сомножитель (N — Ь), увеличив число ее нулей:
= rN — K ) • ( N — Ь ) (2)
и получить дополнительно отталкивающую точку равновесия Ь > 0, что предложил Базыкин для видов с минимально допустимой численностью группы [3]. Альтернативный способ построения обратной связи — раздельно учесть смертность, зависящую от плотности скопления к, и естественную g, много увеличив число параметров:
dN y N 2
— gN — k N 2 ,
—— = r1------ dt y + °N но такая форма триггерной модели трудна для практического использования.
Отметим, что для формы правой части (2) /(N) • (N — Ь) в вычислительных моделях еще необходима компенсирующая сверхбыстрый прирост перенормировка репродуктивного параметра: r 1 ^ г, но движение траектории N (t) ^ 0 выглядит слишком стремительным, безвозвратным вымиранием.
Решение (1), предсказывающее плавный выход к равновесию с замедлением скорости прироста, считается основополагающим, на нем основана теория максимального устойчивого изъятия при управлении биоресурсами, но мало соответствует многообразию встречающихся в экспериментах флуктуаций. Особенно противоречиво для (1) и (2) выглядят экстремальные сценарии популяционных процессов.
Для фундаментальных задач расширения математических методов системной экологии интересно получение моделей нестационарных и переходных режимов. Ограничением при разработке моделей достаточно нетривиальных ситуаций служит обстоятельство, что обосновать можно использование производной не выше первого порядка.
Вспышки численности видов могут проходить по различным сценариям, как с одним затяжными пиком, так и в форме серий кратких всплесков. Предложенная нами ранее непрерывно-дискретная модель с апериодической динамикой описывает только один из возможных сценариев вспышки тропической популяции с бифуркационным завершением [11]. Одним из интересных явлений представляется возникновение всплесков негармонических флуктуаций у насекомых-вредителей. Типичным примером служит поведение кукурузного мотылька Ostrinia nubilalis на Юге России, за численностью которого на всех жизненных стадиях ведутся долгосрочные мониторинговые наблюдения лабораторией ГНУ ВИЗР. Мы кратко рассмотрим свойства колебаний в моделях с запаздыванием, имеющих популяционную интерпретацию в жизненном цикле ряда беспозвоночных, и предложим оригинальные модификации уравнений для учета специфических факторов регулирования выживаемости.
1. Проблема адекватности характеристик колебаний
Решения (1) и (2) плохо согласовывались с наблюдавшимися разнообразного вида флуктуациями популяций. Система дифференциальных уравнений для трофического взаимодействия видов Лотки — Вольтерра позволяет, как известно, получить циклическое решение. Казалось бы, бифуркация рождения цикла (связанная с репродуктивным параметром) в уравнениях перераспределения биомассы может объяснить колебания с отставанием по фазе, наблюдаемые в сообществе организмов. Противоречие в том, что колебания не прекращаются, если сообщество теряет высшее звено трофической цепи, хищника. В лабораторных экспериментах Никольсона [10] установлено, что колебания численности могут появляться у изолированной популяции насекомых, обитающих при постоянных условиях и получающих фиксированное количество корма.
Хатчинсон [6] предложил пересмотреть (1) исходя из запаздывающего действия регуляции, что привело к уравнению с отклоняющимся по времени аргументом «logistic DDE»:
% = rN (t) ( 1 - Y (3) at у К /
Введенное в уравнение запаздывание τ служит характеристикой использования и восстановления ресурсов. Дополнение «репродуктивного» сомножителя запаздыванием в виде rN(t — T i ) • /[N(t), N (t — т 2 )] имеет сомнительное эколого-физиологическое обоснование.
Возникающие в уравнении режимы поведения траектории подробно обсуждались в фундаментальных работах (обычно в однопараметрической форме: С = A^(t)(1 — x(t + + т))), и продолжают исследоваться оригинальными современными методами, как в [1]. При малых значениях запаздывания τ динамика модели опишет затухающие колебания N (t) ^ К .В (3) установлена возможность возникновение бифуркации Андронова — Хопфа с появлением устойчивого предельного цикла N*(t,r). Нарушение устойчивости состояния равновесия зависит от величины гт. Дальнейшее увеличение гт > п/2 вызывает переход в режим релаксационных колебаний. Быстрое возрастание амплитуды колебаний выраженной негармонической формы [8] при увеличении временного промежутка между максимумами и минимумами, стремящимися к неотличимым от нуля значениям, приводят такой релаксационный цикл (рис. 1) к затруднениям при экологическом обосновании.
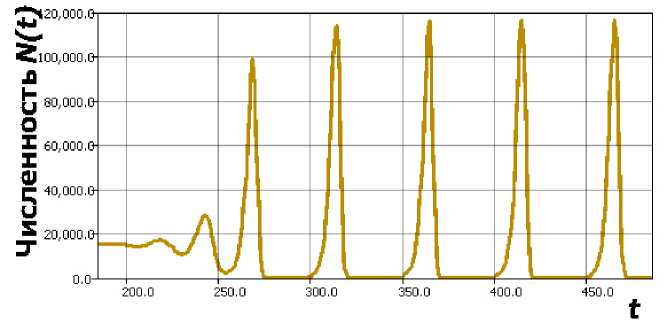
Рис. 1. Релаксационный цикл в уравнении (3), К = 15 000
В аналитическом виде проблема обоснованности цикла модели (3) выражается следующим образом:
min N * (t, X) = exp — e A + 2X +
1 + (1 + X) In X λ
+ -M
Многим лесным насекомым свойственны долгопериодические колебания численности, но вспышки не будут начинаться из глубоких минимумов. Обычно пики следуют после преодоления некоторого порогового значения, когда регуляция естественных врагов становится недостаточной. Формы переходов к флуктуациям для автохтонных и инвазионных популяций могут быть различными, потому продолжают быть актуальными исследования в данном направлении математической биологии, наиболее тесно связанном с теорией колебаний.
В [7] рассматривалась модификация модели Хатчинсона (с приведенными коэффициентами):
dN = X N (t)/ (N(t — 1)),
где /(ж) — дифференцируемая функция, разложимая в асимптотический ряд, для которой выполняются условия:
/(0) = 1, /(ж) = — « + f « 1 , ж ^ю , . > 0. ж 1
(4’)
(4”)
Условиям (4’) соответствует предложенная в [4] функция:
= (1 - ж)
/ (ж) (1 + сж) •
В модификации, известной в англоязычной литературе как «food-limited DDE», расширяется число параметров, определяющих характеристики релаксационного цикла неклассической формы. Так, при увеличении с в (4”) сжимается его амплитуда.
Из дополнительных ограничений при преобразовании исходного уравнения (4) к сингулярно возмущенному ж = F(x(t — 1), е) и далее к предельному релейному уравнению с запаздыванием ж = R(x(t — 1)) предполагается: Л ^ 1. В результате для (4) c (4’) утверждается существование единственного орбитально экспоненциально устойчивого цикла. Неясно соответствие свойств цикла какому-либо нелинейному популяционному процессу, так как из утверждения о характеристиках колебаний в [7] получено:
min N*(t, Л) ~ С1 exp (—Ла0), С1, а0 = const > 0, и как отмечено ранее, λ изначально указывается достаточно большим значением. При использовании функции (4”) наши вычислительные эксперименты показывают влияние демпфирующего колебания параметра с на все характеристики цикла, что напрямую не обсуждается в [7], и требуется условие с ^ 1, так как при малых с свойства цикла (4) будут значительно менее интерпретируемы, чем у (3).
2. Преодоление недостатка цикла min N*(t, Л) ^ +е
Более обосновано, что между выраженными краткими пиками колебаний численность удерживается на значительном уровне. Вернем параметр емкости среды К , неравномерно увеличив степень нелинейности в (4”):
dN АТ/ , / К — N2(t — т) \
If = Т (t ) ((К + cN 3 (t — т))) ’ (5)
тогда в новой модификации удается преодолеть проблему быстрого снижения минимумов min
0
<t
Вычислительные исследования уравнения (5) позволяют говорить о математическом описании частного, но весьма неблагоприятного для лесного хозяйства варианта развития популяционной динамики. После бифуркации можем наблюдать сценарий перехода к релаксационному циклу (рис. 2), соответствующему вспышке численности в виде последовательной серии пиков.
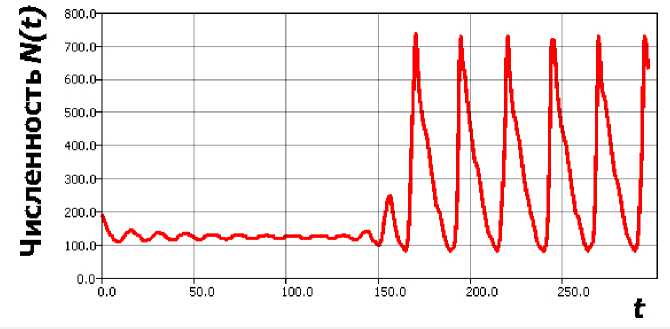
Рис. 2. Переход к релаксационному циклу в новой модели (5)
Основной значимый аспект (5) — очередной стремительный неконтролируемый рост численности начинается от значения близкого к существовавшему перед бифуркацией равновесию, которое является результатом оптимального баланса репродуктивного потенциала и естественных регулирующих факторов.
Согласно всем постулатам системной экологии динамика колебаний (см. рис. 2) может реализовываться только на ограниченном временном интервале. Положим, что достижение значения критической пороговой численности означает не уравновешивание, но деградацию необходимой составляющей среды обитания.
3. Модель с меняющим знак сомножителем
Вспышка численности как переходный нелинейный процесс имеет не только начало, которое мы в (5) отождествляли с бифуркацией Андронова — Хопфа. Дальнейшая динамика ситуации не может быть исчерпывающе описана моделью с глобальным ор-битально устойчивым подмножеством фазового пространства (циклом или хаотическим аттрактором), потому как вспышки — это экстремальные переходные режимы существования вида в среде. Завершение, часто оказывающееся неблагоприятным не только для биосистемы, но и для самой популяции, только в идеальном случае можно трактовать как обратную бифуркацию цикл — устойчивый фокус, то есть с восстановлением балансового равновесия. В уравнении с запаздыванием можно получить описание еще одного специфического явления, которое не было рассмотрено в известных работах.
В случае вспышек насекомых понятие емкости экологической ниши из (1) утрачивает смысл асимптотического предела. Предположим существование предкритического порогового уровня Н < К . Переход через мягкий порог имеет значение для механизмов контроля внутрипопуляционной структуры, что можно отразить изменяющим знак дополнением ^(V), аналогично включающего запаздывание т. Тогда на динамику системы оказывает влияние отклонение [Н — V (t — т)], притом величина отклонения может быть как положительной, так и отрицательной. Модифицируем (3) следующим образом:
^ = ^ (1 — ')(Н — V(t — т)).
at \ К /
Можно считать, что при смене знака отклонения члены правой части (воспроизводства и регуляции) меняются своими функциональными ролями в модели. Для правой части (6) не выполняются условия (4’), указанные для /(ж) при обосновании утверждения о глобальном аттракторе, потому не обязательно теорема (2.1) об орбитальной устойчивости такого цикла из [7] будет справедлива для разработанной нами модели сложной вспышки насекомых.
4. Вычислительный анализ уравнения с двумя τ
При малом значении запаздывания в (6) получаем затухающие осцилляции с V ^ ^ Н . При увеличении т или г 1 в таком уравнении (c г 1 = 10 - 3 г) возникнет притягивающий цикл (рис. 3, К = 15 000, Н = 5 000).
На рисунке 3 динамика после плавного прохождения бифуркационного изменения по сценарию Андронова — Хопфа при переходе г 1 через критическое значение (в вычислительном эксперименте — см. рис. 3 — все параметры модели сохраняются), показывающая установление цикла при V(0) = Н + е,Н = 5 000, К = 15 000.
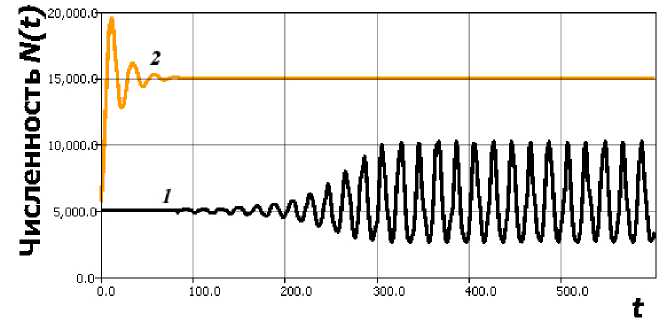
Рис. 3. Притягивающий цикл в новой модели: 1 — цикл после бифуркации в (6);
2 — динамика (3) при аналогичных параметрах
Цикл быстро становится релаксационным с возрастанием г 1 . Из обзора [9] теории колебаний в известных модификациях logistic DDE мы не можем утверждать его глобальную орбитальную устойчивость. Амплитуда колебаний в отличие от аналогичного случая модели (3) не возрастает до нереалистичных величин, но остается в приемлемых границах. В (6) при N (0) < Н переход к установившимся флуктуациям происходит не плавно, но через скачкообразный переходный режим.
Предположим, давление на выживаемость ослабнет совсем. При более резком увеличении значения г 1 т произойдет другое изменение поведения траектории, которая перестанет притягиваться к замкнутому подмножеству фазового пространства. При такой бифуркации траектория системы до установления цикла со все увеличивающейся амплитудой будет резко выброшена за пределы допустимых для ее существования значений при N(t — т) > К . На рисунке 4 ситуация после бифуркации, когда в результате изменения параметра г 1 (в сравнении с аналогичным изменением г в (3) в момент t = 150) траектория в переходных релаксационных колебаниях преодолевает значение К , и далее N (t) ^ то реализует сценарий «кризиса сверхмногочисленного поколения» вплоть до деструкции всей биосистемы.
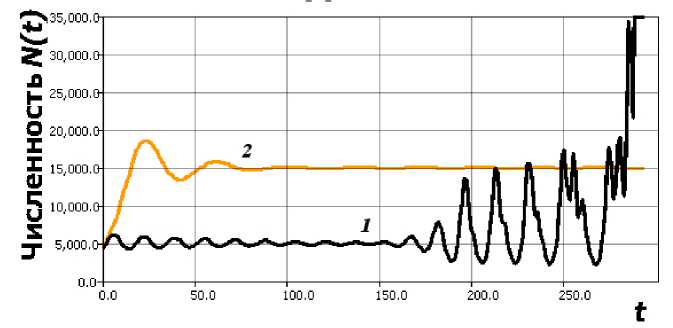
Рис. 4. Релаксационные колебания в новой модели: 1 — выброс за границы емкости среды в (6); 2 — динамика (3) при аналогичном изменении параметра
Цикл сжимается и выбрасывается, вычислительный эксперимент заканчивается сообщением программы о переполнении при вычислениях с плавающей точкой. Такая по- теря неустановившегося режима считается катастрофической. Образуется неограниченное сверху быстровозрастающее немонотонное решение, подобное псевдопериодической функции вида ахп + sinkxp.
5. Объединение новых моделей (5) и (6)
Чтобы лучше представлять, почему не все варианты возникающих в уравнениях с запаздыванием решений имеют теоретическое значение в экологии систем, выпишем уравнение с объединением идей двух предложенных модификаций в следующем виде:
dN Л
К - N 2 (t - т) (К + cN 3 (t - т))
^ (Н - N(t
- т)) ,
увеличивая нелинейность в правой части до кубической. Тогда образующая для N (0) < < Н релаксационный цикл траектория при уменьшении с начнет достаточно параболически плавно и неограниченно возрастать (рис. 5, с 0 = 0.11, бифуркационное С = 0.1, т = 8).
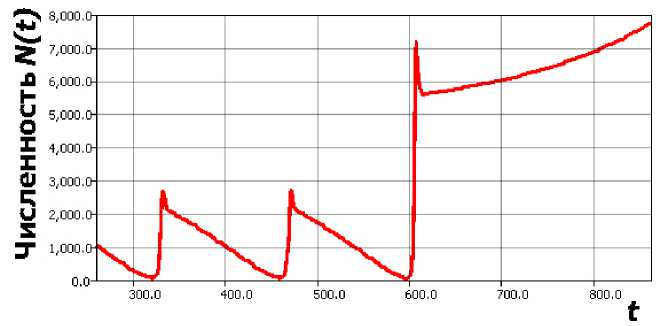
Рис. 5. Медленный сценарий ухода траектории из цикла в (7)
Подобный путь потери решением свойства диссипативности видится не обоснованным и сценарий популяционной динамики вряд ли реализуется. Мы рассматривали ситуацию изолированной саморегулируемой популяции, потому должно присутствовать ограниченное сверху предельное состояние (равновесие, цикл или даже устойчивая по Пуассону хаотическая траектория), либо происходит деструкция биосистемы скачкообразно.
Заключение
При совершенствовании модели специфического сценария популяционной динамики насекомых, связанной с улучшением характеристик колебаний, мы получили уравнение, поведение решения которого описывает катастрофическое завершение серии пиков численности после бифуркации Андронова — Хопфа. В современном обзоре по применению различных уравнений с запаздыванием (в том числе с более чем одним τ) [12] в математической биологии сценарий с разрушением автоколебаний не рассматривал- ся. Подобные свойства интересны для теоретической системной экологии, потому как относятся к анализу значительных трансформаций биоценозов.
В уравнении обосновано значение Н мягкого порогового состояния, в отличие от явной нижней критической точки L в (2) и жесткого уровня остановки прироста К в (1). Особенность предложенной модели возникновения/завершения взрывообразного популяционного процесса в том, что вместо дальнейшего увеличения амплитуды колебаний релаксационной формы при ослаблении факторов регуляции происходит выброс траектории в режим за рамками наличия условий дальнейшего прироста численности.
Некоторым популяциям вредителей действительно свойственно специфическое нерегулярное явление осциллирующей вспышки численности. Пример таких колебаний приведен на рисунке 6 с тремя выраженными пиками из [5]. В результате регулярной гибели леса на протяжении 30 лет происходит завершение атипичной вспышки, так же внезапно, как и началось ее развитие.
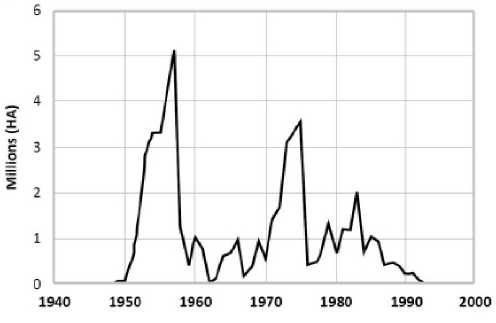
Рис. 6. Пилообразная вспышка листовертки в масштабах гибели леса
После вспышки в очаге индекс видового разнообразия претерпевает существенные изменения, соответственно область перестает быть пригодной для воспроизводства популяции.
Исследуемые нами в рамках проектов РФФИ сценарии резких колебаний численности вредителей и промысловых видов отличаются своей нерегулярностью возникновения. Отметим, что весьма популярна гипотеза значительной синхронизированно-сти популяционных изменений насекомых с гелио-геофизическими факторами. Однако даже при построении альтернативных моделей с учетом периодически меняющейся солнечной активности или современных представлений об опосредованном действии Форбуш-эффекта (резкое понижение интенсивности галактических космических лучей) необходимо аналогично рассматривать запаздывающее действие внешних влияний.
Список литературы Разрушение релаксационных колебаний в новой модели экстремальной динамики численности популяции
- Кащенко, C. А. Динамика логистического уравнения, содержащего запаздывание/C.А. Кащенко//Математические заметки. -2015. -Т. 98. -C. 85-100.
- Bacaer, N. A Short History of Mathematical Population Dynamics/N. Bacaer. -London: Springer-Verlag, 2011. -198 p.
- Bazykin, A. D. Nonlinear Dynamics of Interacting Populations/A. D. Bazykin. -London: WSP, 1998. -198 p.
- Gopalsamy, K. Time lags in a «food-limited» population madel/K. Gopalsamy, M. Kulenovic, G. Ladas//Applicable Analysis. -1988. -Vol. 31, № 3. -P. 225-237.
- Gray, D. Historical spruce budworm defoliation records adjusted for insecticide protection in New Brunswick/D. Gray//Journal of the Acadian Entomological Society. -2007. -Vol. 115, № 1. -P. 1-6.
- Hutchinson, G. An Introduction to Population Ecology/G. Hutchinson. -New Haven: Yale University Press, 1978. -234 p.
- Kolesov, A. A modification of Hutchinson’s equation/A. Kolesov, E. Mishchenko, Yu. Kolesov//Computational Mathematics and Mathematical Physics. -2010. -№ 12. -P. 1990-2002.
- Kolesov, A. Relaxation Oscillations in Mathematical Models of Ecology/A. Kolesov, Yu. Kolesov. -Rhode Island: AMS, 1993. -128 p.
- Ladas, G. Oscillation and global stability in a delay logistic equation/G. Ladas, C. Qian//Dynamics and Stability of Systems. -1994. -Vol. 9, № 2. -P. 153-162.
- Nicholson, A. An outline of the dynamics of animal populations/A. Nicholson//Australian Journal of Zoology. -1954. -Vol. 2. -P. 9-65.
- Perevaryukha, A. Yu. A model of development of a spontaneous outbreak of an insect with aperiodic dynamics/A.Yu. Perevaryukha//Entomological Review. -2015. -Vol. 95. -P. 397-405.
- Ruan, R. Delay Differential Equations in Single Species Dynamics./R. Ruan//Delay Differential Equations and Applications. -Berlin: Springer, 2006. -P. 477-517.


