Разрывный метод Галеркина в задачах газовой динамики с негладкими решениями

Разрывный метод Галеркина (Discontinuous Galerkin — DG) [1] хорошо зарекомендовал себя как метод высокого порядка точности при решении широкого круга задач газовой динамики. Интерес к методам типа DG обусловлен не только возможностью достижения высоких порядков аппроксимации, но и эффективностью распараллеливания благодаря небольшой области зависимости решения в одной вычислительной ячейке от решений в соседних ячейках. В задачах с гладкими решениями метод достигает высоких порядков точности в неизменном виде, но наличие негладких решений и разрывов неизбежно вызывает нефизические осцилляции.

Существуют различные способы борьбы с подобными осцилляциями. Например, можно не использовать высокие порядки локальных аппроксимирующих многочленов. При этом появляется возможность применения лимитеров различных типов, разработанных для методов конечных объемов. Известны также способы борьбы с осцилляциями путем локального понижения порядка разложения.

Имеется иной подход к борьбе с нефизическими осцилляциями. В его основе лежит специальное представление данных в методе DG [2]. Известны по крайней мере два способа их хранения. При первом способе — Modal, для каждого элемента разбиения области решения в памяти хранится набор коэффициентов разложения решения по локальному базису функций. Второй способ — Nodal, предполагает хранение значений решения в некоторых точках элемента. Оба метода представления эквивалентны с математической точки зрения, ибо переход от одного к другому происходит за счет матрицы преобразования, однозначно определенной для данного набора точек и семейства многочленов на элементе [2]. Далее метод будет описан более подробно.

В данной статье предлагается использовать Nodal-представление для подавления нефизических осцилляций в совокупности с одним из методов, предназначенных для разностных схем, а именно с монотонизатором Жмакина–Фурсенко [3]. Этот подход дополняется индикатором гладкости, разработанным в [4] и протестированным на одномерных задачах распада разрыва: задаче Сода [5], задаче Шу–Ошера [6], задаче разлета двух масс газа. Помимо этого в статье применяется авторский метод реализации численного алгоритма на языке Си со специализированным интерфейсом на языке Python.

2.    Описание метода DG

Разрывный метод Галеркина представляет собой сочетание методов конечных объемов и конечных элементов. Расчетная область имеет вид набора ячеек (элементов). В каждой ячейке решение раскладывается по некоторому базису функций, обычно этот базис состоит из многочленов. Разложение решения по базису локально, то есть на границах между элементами не накладывается условие непрерывности искомых функций как в методе конечных элементов; здесь ячейки «разъединены».

При таком подходе на каждой границе между ячейками возникает неоднозначность: свое решение для каждой из соседних ячеек. Чтобы исключить эту неоднозначность, на границах, подобно методу конечных объемов, вместо искомой величины используется ее поток. Таким образом, область зависимости решения в каждой ячейке образуют лишь ее непосредственные соседки.

Рассмотрим задачу

— + ^ 0 = о,    x _eQ ,   _{q = [} l , r ],

dt    dx где L, R — левая и правая границы отрезка соответственно. Представим Q приближенно при помощи K непересекающихся ячеек Q ® Qh = U Dk. Теперь разложим решение задачи (1) в каждой ячейке по базису k из N многочленов порядка от 0 до N = Np -1:

NpNp x е Dk : uk(x, t) = Eйn Vn(x) = Euk(x, t)li (x). n=1                   i=1

В записи этого локального решения показаны оба способа представления: Modal и Nodal. Modal предполагает хранение коэффициентов разложения й k по базису { v n } в каждой ячейке, Nodal — разложение по базису из интерполяционных многочленов Лагранжа { l i }, что фактически соответствует хранению значений функции u^k_k ( x^k , t ) в некоторых точках внутри элемента. Выбор точек хранения основан на оптимизации обусловленности матриц, возникающих при решении задач. Переход между представлениями осуществляется при помощи матрицы Вандермонда для данного базиса многочленов и точек разбиения на элементе [2].

В задаче (1) базис { v „ } состоит из ортогональных многочленов, которые обозначим как { P_n }. Тогда

Np для некоторого набора {сi} из Np точек справедлива формула u(Ei) = EU nPn_,(Ei). Теперь можно записать n=1

уравнение перехода между двумя представлениями: Vu = u , где V_y = Р _{у - 1}( Е i ), u i = U i , u i = u ( E i ); V — локальная матрица Вандермонда. После умножения обеих частей исходного уравнения (1) на каждый из многочленов базиса и интегрирования по частям получим:

J f^ ^U ^ V n ^{+ d f} h ^{( U} h ) ^V n dx = J n ■ ⁽ f hk ⁽ О ^- f ‘⁾ V n dx ,                           ⁽²⁾

Dk I dt          dx J        8Dk где n — внешняя нормаль к элементу, f — численный поток на границе между элементами.

Для удобства обозначим информацию из внутренней части элемента индексом « - », а информацию извне индексом « + ». Тогда среднее значение на границе запишется как {{ u }} = ( u " + и ^/2, где и может быть как скаляром, так и вектором. Похожим образом введем скачок вдоль нормали n : И u ]] = n ^- u ^- + й ⁺ u ⁺ . Многие выкладки удобнее проводить для некоторого «базового» элемента I ;

в одномерном случае — это отрезок I = [ - 1,1].

Вернемся к рассмотрению численного потока. В данном случае используется поток Лакса-Фридрихса

Xl n

— собственное

f* = fLF ={{fh (uh)}} + C[[uh ]]/2, где C определяется локально как C = max u значение матрицы. Действия с потоком Лакса-Фридрихса обычно наиболее просты, хотя возможно применение и других численных потоков.

Перейдем теперь к локальным операциям, необходимым непосредственно для вычислений в задаче. Начнем с матриц M ^k и S ^k . Матрицу масс M определим следующим образом:

xrk

Mk= lk(x)lk(x)dx=h   l(r)l (r)dr=hkM2,(3)

ij                j              2 J,        jj где коэффициент перед полученной матрицей масс M Для разложения по семейству ортогональных

— это якобиан перехода к базовому элементу I . многочленов формулу (3) перепишем в виде:

Mk = hM/2 = hk (VVT) 1/2 . Матрицу жесткости Sk зададим как S j, = f l* (r)  j( ) dr = S*j. Для простоты ее dr

— 1

расчета определим матрицу дифференциирования с элементами

в виде D

dl _j

=.Отсюда следует dr

равенство: MD _r = S .

duk xrk xlk

Теперь исходное выражение (2) можно представить в виде: M ^k —- + Sf h ^k = Г 1 ^k ( x )( f_h — f ) ! dt

(промежуточные выкладки опускаем, так так они приведены в [2]). Полученную полудискретную задачу осталось проинтегрировать по времени. Интегрирование по времени можно производить разными методами. В данном случае используются методы Рунге–Кутты. Такой подход называется Runge–Kutta Discontinuous Galerkin — RKDG. Акцент на форме хранения данных делается намеренно, так как их представление играет существенную роль при применении описываемого подхода.

3.    Метод борьбы с нефизическими осцилляциями

При способе Nodal DG хранятся значения функции решения, соответствующие некоторому набору точек внутри каждого элемента. Воспользуемся этим при проведении монотонизации.

В данной статье в основе метода монотонизации лежит подход [3], основанный на принципе избирательной диффузии–антидиффузии. На первом этапе вводится искусственная диффузия во всех точках, на втором — избирательная измененная антидиффузия. Опишем эти процессы подробнее.

Пусть имеется некоторый набор значений { f_i }. Определим оператор диффузии D : Df = Ф * +ш — Ф / — 1/2 = Q ⁵ f + 1/2 — Q ⁵ f — 1/2 , где 5 f + 1/2 = f + i — f , Q — постоянный коэффициент, точное значение которого зависит от конкретной задачи (хорошие результаты обычно получаются при значениях от 1/10 до 1/6). Получим набор значений { f }. Теперь исключим диффузию таким образом, чтобы не возникли новые экстремумы и не усилились уже существующие. Для этого в операторе антидиффузии A = — ( ф * ^: _{+ 1/2} — ф С _{— 1/2} ) ограничим значения ф * _{+ 1/2} = 5 f _{+ 1/2} условием Ф c + 1/2 = ^{5 max{0,min(} 5 ⁵ f — 1/2 , I Ф * + 1/2 I, 5 ⁵ f + 1/2 ^)} , где ⁵ = ^si g ⁿ⁽ Ф _i + 1/2 ⁾ .

Метод монотонизации Жмакина–Фурсенко разрабатывался для борьбы с нефизическими осцилляциями в разностных схемах. Заметим, что метод работает с некоторым массивом значений. При способе хранения Nodal DG фактически тоже создается массив значений, и цель данной работы состоит в том, чтобы подвергнуть его процедуре монотонизации Жмакина–Фурсенко и оценить ее целесообразность в газодинамических задачах с негладкими решениями.

Рассмотрим постановки различных задач. Для этого запишем уравнения Эйлера в одномерном случае:

^P+^M = 0, dtd

, d(pu) + d(pu)2 +dp =o dt       dx     dx’ de + Ui e + p) u) =0 d t       dx’ где e = p/(y — 1) + p u 2/2. Для задачи Сода (Sod problem) начальные условия слева (индекс L) и справа (индекс R ) на отрезке [0, 1] имеют следующий вид: pL =1,0; uL =0,75; pL =1,0; pR =0,125; uR =0,0; pR = 0,1 ; x0 = 0,3 ; T = 0,2 , где x0 — граница разрыва в начальный момент времени, T — полное время реализации задачи.

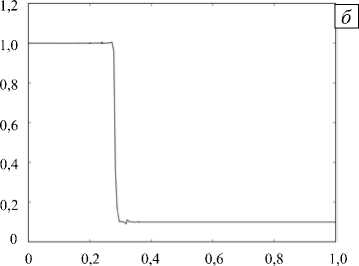
Применим описанный подход к решению задачи Сода. В отсутствие процедур сглаживания уже на первых шагах по времени возникают нефизические осцилляции. При числе ячеек K = 25 и локальном порядке многочленов N = 5 проанализируем график давления на примере одной вычислительной ячейки.

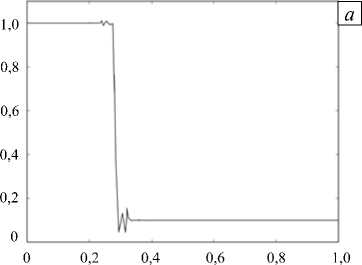
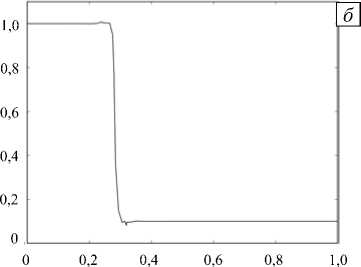
Рис. 1. Задача Сода; график давления p ( x ) без монотонизации ( а ) и с монотонизацией ( б )

Как видно из рисунка 1, а , нефизические осцилляции возникают в самом начале счета (на графике изображен второй шаг по времени). Со временем осцилляции нарастают очень быстро, что приводит к появлению отрицательных плотностей и давлений, поэтому нет возможности изобразить решение даже на десятом временном шаге. При использовании метода монотонизации Жмакина-Фурсенко удается существенно уменьшить осцилляции (Рис 1, б ); в этом случае ударные волны локализуются в пределах одной вычислительной ячейки. Из дальнейших примеров будет видно, что контактный разрыв локализуется в нескольких ячейках.

Полученные после проведения полного расчета в задаче Сода результаты представлены на рисунке 2. Графики давления и плотности в конечный момент времени свидетельствуют, что контактный разрыв не локализуется в одной ячейке, а наблюдается в пределах нескольких из них. Это происходит не только вследствие применения процедуры монотонизации, но и из-за диссипативных свойств потока Лакса-Фридрихса.

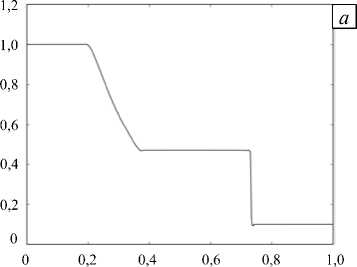
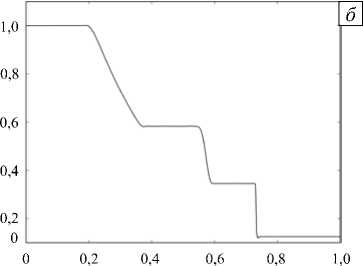
Рис. 2. Задача Сода; график давления p ( x ) ( а ) и плотности р ( x ) ( б ); T = 0,2; K = 100; N = 7

Употребим метод монотонизации в задаче разлета двух масс газа. Для этого запишем начальные условия слева и справа на отрезке [0, 1]: р L = 1,0; u_L = - 1,0; p_L = 1,0 ; р R = 1,0; u_R = 1,0; p_R = 1,0; x ₀ = 0,5; T = 0,1. В решении данной задачи отсутствуют разрывы, но оно не является гладким, поэтому при вычислениях уже на первых шагах по времени возникают нефизические осцилляции. Из рисунка 3, а видно, что область отрицательного давления зарождается на втором шаге по времени (фактическое давление получается меньше нуля, но на рисунке 3, а график заменен на зеркальный для удобства сравнения с рисунком 3, б ), так что расчет не может быть продолжен.

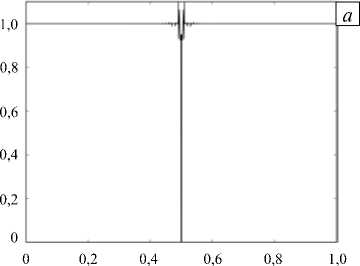
Рис. 3. Задача разлета масс газа; график давления p ( x ) без монотонизации ( а ), с монотонизацией ( б )

1,0

0,8

0,6

0,4

0,2

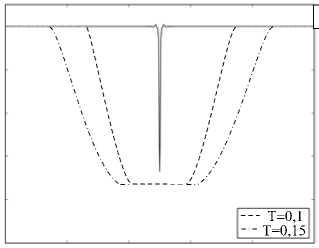
б

о

0,2       0,4        0,6       0,8        1,0

Теперь применим алгоритм монотонизации. Результат показан на рисунке 3, б , из которого видно, что область отрицательного давления подавлена и вычисления можно продолжить. На рисунке 3, б также приводятся графики давления, соответствующие моменту T = 0,1 и полному времени расчета T = 0,15 . Промежуточный график свидетельствует, что алгоритм монотонизации не меняет значения давления в нижней точке с течением времени. При этом существенные осцилляции в решении отсутствуют.

Рассмотрим еще одну задачу — задачу Шу–Ошера (Shu–Osher problem) [6]. Запишем граничные условия на отрезке [0, 1]: ρ _L = 3, 857143; u_L = 2, 629369; p_L = 10, 333333; ρ _R =1, 0 + 0, 2sin(50 x ); u_R = 0,0; p_R =1,0; x ₀ =0,1; T =0,18.

Известно, что при движении скачка должны возникать осцилляции плотности большей частоты, чем исходные. Возьмем описанный метод монотонизации и проверим, сохраняются ли в решении физические осцилляции. Из рисунка 4 видно, что удается побороть нефизические осцилляции и не утратить при этом физические.

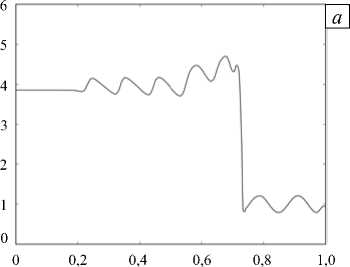
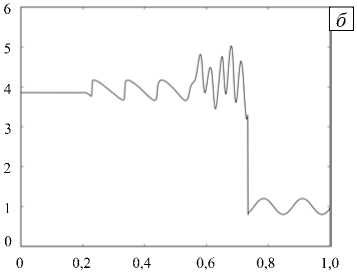
Рис. 4. Задача Шу–Ошера; график плотности ρ ( x ) в момент времени T = 0,18 при разном числе ячеек K : 100 ( а ), 1000 ( б )

Монотонизатор можно применять не только на всей области, но и в ее локальных зонах. Для выявления зон, где необходима процедура сглаживания, можно использовать детектор разрывов, разработанный в [4]. Этот алгоритм основан на выявлении вклада коэффициента при многочлене старшей степени в Modal-представлении.

Согласно выводам авторов метода, при убывании коэффициенты разложения должны иметь тот же

N ( p )

порядок, что и коэффициенты разложения Фурье. Если записать решение в виде u = ∑ u_i ψ _i и рассмотреть i =1

N ( p - 1)

~ _ ( u — й, u — О) S=

(u, u)

AV усеченное разложение u =

∑ u_i ψ _i , то индикатор гладкости можно представить в виде: i =1

Полученный индикатор S позволяет успешно определить ячейки, в которых появляются осцилляции.

Продемонстрируем результаты использования детектора разрывов на первых шагах по времени в задаче Сода. На рисунке 5 показан график давления на втором шаге по времени. Из рисунка видно, что решение в зоне разрыва после применения алгоритма монотонизации стало более гладким, то есть, детектор разрывов сработал.

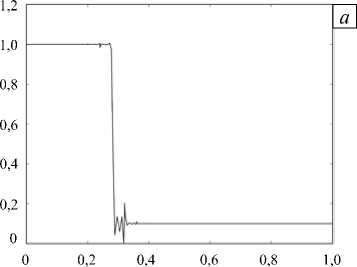
Рис. 5. Задача Сода; график давления p(x) с неактивным (а ) и активным (б) детектором разрывов

4.    Программная реализация алгоритма борьбы с нефизическими осцилляциями

Численный алгоритм реализован на языке Си. Интерфейс взаимодействия с алгоритмом написан на языке Python. В интерфейсе осуществляется задание начальных данных и вывод результатов, само решение задачи происходит в функциях языка Cи. Особенностью данной реализации является метод связи интерфейса с расчетным алгоритмом. Суть его заключается в том, что при каждом запуске программы происходит модификация вычислительного кода на Cи: начальные данные, их размеры, матрицы преобразования записываются в код в виде констант, а также допускается полуавтоматическое разворачивание циклов, упрощение адресации многомерных массивов и автоматическое копирование практически идентичных участков кода. Эти возможности позволяют не только избежать многократного копирования похожих участков кода, но и ускорить его выполнение за счет разворачивания циклов и задания большого числа данных как констант.

Рассмотрим эти процессы подробнее. Довольно проблематично из других языков программирования передавать в функции языка Cи многомерный массив (то есть массив указателей). Намного проще транслировать одномерный массив и рассматривать его как многомерный. Для этого нужно пересчитывать индексы нового массива исходя из размеров частей, на которые условно делится исходный массив. В данной программной реализации применяется прием, позволяющий для некоторых частей одномерного массива использовать вместо одного два индекса и тем самым имитировать адресацию многомерного массива. На это нацелено одно из преобразований, которые проходит вычислительный код после запуска интерфейса программы, при этом два индекса фактически пересчитываются в один с учетом размерности массива.

Другая задача — это избежание повторения участков кода, отличающихся друг от друга, например, лишь названием переменных при неизменных операциях с ними. Для ее решения пускается в ход механизм шаблонов, в котором при помощи специальных управляющих команд можно нужное количество раз продублировать участок с различными параметрами.

После формирования конечного кода происходит его компиляция и запуск счета. Причем все процессы, связанные с модификацией и компиляцией кода, а также его вызов запускаются из управляющего интерфейса, то есть исключается необходимость выполнять эти этапы вручную.

5.    Заключение

Описанный подход к монотонизации, разработанный изначально для разностных схем, позволяет успешно бороться с нефизическими осцилляциями при использовании разрывного метода Галеркина. Созданный на его основе алгоритм прошел проверку на задачах распада разрыва: проблеме Сода, проблеме разлета двух масс газа, а также, проблеме Шу–Ошера. При этом удается достичь разрешения ударных волн в пределах одного–двух элементов, контактных разрывов — в пределах трех–четырех элементов. Метод монотонизации работает достаточно быстро благодаря своей простоте. Главное преимущество этого подхода состоит в том, что не требуется явная модификация логики расчета разрывным методом Галеркина.