Развитие длинных усталостных трещин в стальных образцах под действием движущихся тепловых полей

В задачах разрушения традиционно рассматривался случай действия механической нагрузки. Если нагрузка превысит некоторое критическое значение, то после старта трещина обычно развивается динамически вплоть до полного разрушения конструкции (разделения на части). Поэтому для оценки прочности конструкции определяется нагрузка начала неустойчивого развития трещины. В случаях, где разрушение происходит под действием самоуравновешенных полей напряжений (остаточные, тепловые, и др. напряжения) обычно используется тот же подход. Однако область растяжения у таких полей является локальной и часто невелика по сравнению с размером конструкции. Поэтому рост квазистатической или усталостной трещины, которая не выйдет за пределы этой области (случай динамического распространения трещин, характерный для материалов низкой вязкости, рабочая температура которых ниже первой критической, в данной работе не рассматривается), не может привести к полному разрушению.

Другая крайняя точка зрения заключается в том, что трещина не может развиться до опасного размера вне зависимости от характера поля напряжений: является оно неизменным во времени (например, остаточным) или изменяющимся во времени (например, тепловым). Действительно, если источники тепла неподвижны, то поле напряжений будет изменяться во времени по закону, близкому к пропорциональному. В этом случае, хотя величина напряжений меняется, область теплового растяжения не может существенно изменяться по размеру, и длина растущей трещины оказывается ограниченной этим размером так же, как под действием остаточных напряжений. Так при внезапном охлаждении одной грани у предварительно нагретой стеклянной пластины возникает сетка трещин, развивающихся от этой грани (рис. 1, а).

а)                                                                    б)

Рис. 1. Тепловые трещины от неподвижных источников тепла

После достижения максимальной длины трещины перестают расти и при последующих циклах нагружения не меняются. Если деталь выполнена из пластичного материала, то может происходить усталостное распространение трещины (трещин) как, например, для валка установки произ-

водства шлаковаты (рис. 1,6). Однако максимальный размер трещин также оказывается ограниченным областью растягивающих напряжений.

Из практики эксплуатации известны случаи разрушения теполонаг-руженных конструкций, когда трещины достигли длины, сравнимой с размером конструкции. Это хранилище фосфорной кислоты, в котором трещина длиной около 3 м развилась вдоль образующей цилиндрического" корпуса от основания (рис. 2, а), когда в холодное хранилище заливалась горячая кислота [8] (перепад температур около 100 °C). Трещины большой длины также возникают в чугунных а)                         б)             сталеразливочных изложницах, дос

Рис. 2. Тепловые трещины большого размера           тигая Длины, близкой к размеру кон струкции [5] (рис. 2, б). В чаше шла-ковоза после возникновения трещин они на протяжении ряда циклов заполнения шлаком вырастают до размера, превышающего область теплового растяжения [4].

Это явление объясняется с учетом движения теплового поля. В приведенных примерах это движение вызывается изменением уровня теплонесущих сред: кислоты в хранилище, расплава при заливке изложницы, жидкого шлака при заполнении чаши шлаковоза. В работе [3] в результате расчетных исследований были продемонстрированы и исследованы два основных квазиста-тических механизма разрушения конструкций при таком нагружении. Это, во-первых, сонаправ-ленный рост трещины, когда ее вершина растет по направлению движения поля температур и связанного с ним поля напряжений, постоянно оставаясь в области высоких напряжений. Во-вторых, это противонаправленный механизм, когда вершина трещины подрастает навстречу движущемуся полю. При этом ее приращение за один цикл, как и в случае неподвижного теплового поля, ограничено областью теплового растяжения. Однако по мере роста числа циклов нагружения (проходов поля) это приращение быстро накапливается, и так же, как в случае сона-правленного механизма, будет ограничено только размером области движения поля напряжений.

Разрушение по этим механизмам было получено в цилиндрических тонкостенных образцах из силикатного стекла, под действием полей, движущихся вдоль оси цилиндра [10]. Целью настоящей работы является исследование развития длинных трещин под действием движущегося теплового поля на малоразмерных лабораторных образцах, которые изготовлены из стали, обладающей сравнительно высокой вязкостью разрушения.

Методика эксперимента

Во-первых, потребовалось определить условия эксперимента, обеспечивающие подрастание трещины. Эта проблема вызвана значительной вязкостью конструкционной стали, из которой изготовлен образец. В задачах линейной механики разрушения интенсивность напряжений в вершине трещины пропорциональна квадратному корню из характерного линейного размера задачи, который для исследуемых механизмов равен размеру зоны растяжения. Создание условий, приводящих к росту трещины, представляет трудность, так как лабораторные образцы ограничены малым размером. Поэтому условия нагружения должны быть максимально жесткими для трещины, при этом наибольшая температура в эксперименте не достигать температуры фазовых превращений в стали.

Образец представляет собой длинную тонкостенную цилиндрическую оболочку внешним диаметром 69 мм и с толщиной стенки 4 мм, изготовленную из стали 30ХГСА. Тепловое поле с высокими градиентами температур создавалось путем интенсивного нагрева образца в кольцевом индукторе генератора токов высокой частоты и охлаждения струей холодной воды, вытекающей из трубки (рис. 3). Вращение образца механическим приводом с частотой 0,85 мин-1 обеспечивало движение теплового поля в форме пятна по окружности образца.

Установившееся тепловое поле является квазистацио-нарным относительно неподвижной системы координат, связанной с индуктором. Трещина должна развиваться вдоль линии движения теплового поля, т.е. по окружности образца, так как при этом для такой трещины достигается наибольшая напряженность в ее вершине.

Расчеты, выполненные для описанной схемы нагружения свободного образца (без внешних сил и связей), показали, что такого нагружения недостаточно для роста трещины любой длины. Кроме того, в образце из пластичного материала происходит циклическое пластическое деформирова

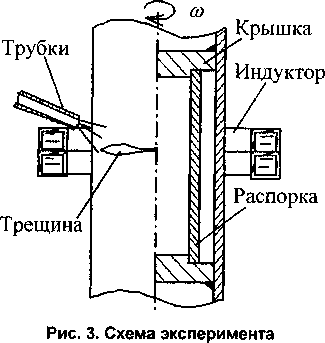
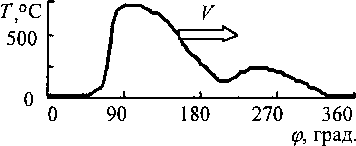
Рис. 4. Изменение температуры по окружности образца

ние с уменьшением длины образца и увеличением толщины стенки в плоскости индуктора: механизм роста ребра [4]. Поэтому концентратор (отверстие, окружная выточка, начальная трещина) обжимается и разрушение не происходит.

Внутрь образца для предотвращения осевого сжатия была вставлена распорка, упирающаяся в крышки, закрепленные в образце (см. рис. 3). В течение начального периода нагружения, пока усилие от распорки мало, в образце активно происходит циклическое пластическое деформирование в осевом направлении. После периода стабилизации, когда усилие в распорке достигает предельного значения, в рабочем цикле происходит лишь знакопеременное течение без прогрессирующего формоизменения.

Распределение температур в цикле нагружения было определено при помощи термопар, приваренных на поверхностях образца. Усилие, действующее со стороны распорки на образец, было рассчитано по методике, разработанной в [И], из условия отсутствия прогрессирующего формоизменения в образце в стабильном цикле при данных условиях нагружения. Осевое напряжение в образце от этого усилия составило ст? = 85 МПа.

Расчетное исследование роста трещины, реализуемого в эксперименте

Определение наиболее опасного положения вершины трещины

Так как наибольшие напряжения достигаются в плоскости симметрии задачи - плоскости индуктора, рассмотрим рост трещины, лежащей в этой плоскости.

Распределение температур в этой плоскости по окружности образца, полученное в результате термометри-рования, показано на рис. 4. Вектор V показывает направление движения поля температур и связанного с ним поля напряжений (осевые напряжения показаны на рис. 5, а) по отношению к образцу. Температура точки образца плавно повышается по мере нагрева в индукторе и резко падает, когда точка попадает под охлаждающую струю жидкости. В этой зоне возникают высокие градиенты температур, и, следовательно, напряжений.

Трещина, отвечающая случаю роста вершины по направлению движения поля, показана на рис. 5, б разделенной на две части, ее подрастающая вершина имеет координату ^с. Схема роста противоположной вершины показана на рис. 5, в, где через М обозначено приращение трещины за цикл. Следует отметить, что в обоих случаях растущая вершина трещины находится в зоне растяжения, которая соответствует охлаждаемой области, где материал имеет пластические свойства и вязкость ст-, МПа

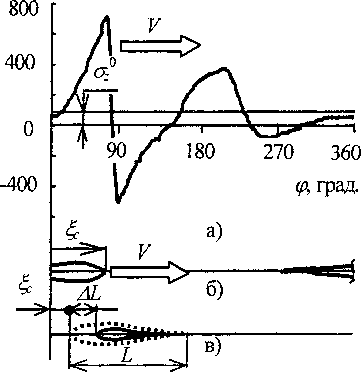
Рис. 5. Зависимость осевого напряжения от окружной координаты:

а, б - сонаправненный механизм роста; в - противонаправленный механизм роста

разрушения, соответствующие нормальной температуре.

Во-первых, требуется определить наибольшее значение коэффициента интенсивности напряжений maxA^i для всех взаимных положений трещины и теплового поля, характеризуемых 4с, для обоих возможных направлений роста, так как именно maxKi определяет возможность разви тия трещины.

Расчет номинальных (при отсутствии трещины) термоупругих напряжений выполнен методом конечных элементов (МКЭ) на той же модели, в которой затем проведен расчет с трещиной, но с закрепленными узлами на линии трещины.

Для определения коэффициента интенсивности напряжений Ку использовался известный метод, согласно которому значение Ку определяется интегрированием номинальных напряжений по всей длине трещины при помощи функций Грина, которые для данного тела равны значению Ку от сосредоточенных сил, приложенных к берегам трещины. Для оценки Ку была использована модель бесконечной пластины с прямой конечной трещиной, для которой известно аналитическое выражение функций Грина [9]. В случае растущей вершины трещины по схеме, отвечающей рис. 5, б, расчетное выражение для коэффициента интенсивности напряжений принимает вид

Ку = № £ а₂ & - ^[T^d^, (1)

где L - длина трещины, q = Кф - дуговая координата в образце, 4с - координата вершины трещины, cr_z - номинальные осевые напряжения в цилиндре, действующие вдоль линии трещины (рис. 5, а).

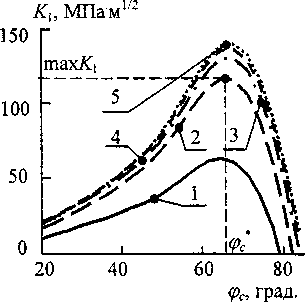
Рис. 6. Зависимость коэффициента интенсивности напряжений от координаты вершины трещины для ряда длин трещины: 1-5 мм; 2-35 мм; 3-65 мм; 4 - 95 мм; 5 -125 мм

Зависимости Ку от угловой координаты вершины трещины ф_с для ряда длин трещин и сонаправленного мехпоказаны на рис. 6. Из графиков видно, что длина трещины незначительно влияет на координату ее вершины ф* (показана для кривой 3), при которой обеспечивается тахК]. Это объясняется высокими градиентами напряжений: с удалением вершины трещины от зоны высоких напряжений напряженность в ней быстро уменьшается. Аналогичный результат получен и для случая роста второй вершины трещины.

Полученные значения фс* для ряда длин трещин использовались далее в более точных расчетах для опреде- ления тахК] с использованием МКЭ.

Численное определение параметров разрушения

Конечно-элементная (КЭ) модель реализована в пакете ANSYS. Разбиение и поле осевых напряжений показано на рис. 7, а (для сопоставления на рис. 7, б показан образец с трещиной). В силу симметрии задачи относительно плоскости индуктора рассчитывалась половина образца. В модели использовались восьмиугольные объемные элементы с линейными функциями формы. Сгущение сетки выполнено в зонах высокого градиента температур и в области вершины трещины. В отличие от аналитической оценки, рассмотренной в предыдущем пункте, в данной модели заложена реальная диаграмма деформирования (учет пластических свойств и зависимости механических свойств от температуры) и посредством контактных элементов учтена возможность смыкания берегов трещины. Определенное ранее напряжение от распорки сг° = 85 МПа приложено к торцам модели. Тепловое поле задавалось МКЭ по результам термометрирования.

Использование традиционной формулировки J-интеграла [13] в задачах, где присутствует неравномерное тепловое расширение, как показано в [1], приводит к неверным результатам. Поэтому по результатам конечноэлементных расчетов напряженно-деформированного состояния определялись значения ^-интеграла в обобщенной формулировке [12]. В отличие от традиционной формулировки, ^-интеграл позволяет учесть неоднородность тепловых расширений внутри области интегрирования.

• а) б)

Рис. 7. Окружная трещина в цилиндрическом образце: а - КЗ расчет (осевые напряжения); б - результат эксперимента

Коэффициент интенсивности напряжений рассчитывался по значениям ^-интеграла по формуле К_х = -jj^E , где Е - модуль упругости материала, применимой для плоского напряженного состояния в вершине трещины, которое имеет место в данной задаче.

По результатам расчетов построены зависимости тахК| от длины трещины L как для случая роста трещины против движения теплового поля (рис. 8, а), так и для случая роста по направлению движения - рис. 8, б. Для сравнения вместе с результатами расчета МКЭ показаны зависимости, полученные по оценке (1).

КЭ расчеты показали, что при росте трещины против движения поля происходит смыкание ее берегов, так как ее линия проходит через зону сжатия. Это приводит к тому, что при увеличении длины трещины длина ее раскрытой части не меняется. Из рис. 8, а видно, что в первом приближении величину тахК] можно считать неизменной для трещины длиной от L = 1 см до L = 9 см (от короткой трещины до 150° окружности образца), и рост трещины будет автомодельным.

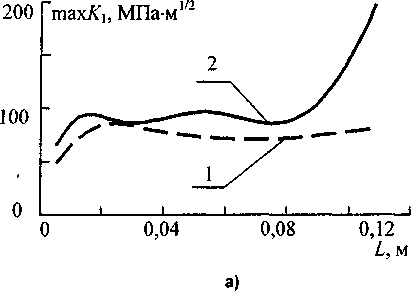
Рис. 8. Зависимость наибольшего коэффициента интенсивности от длины трещины (1 - аналитическая оценка, 2 - КЭ расчет): а - при росте трещины против движения поля; б - в том же направлении

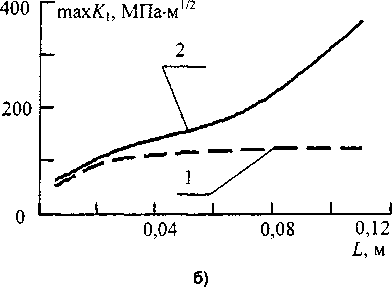
В случае роста в направлении движения поля тахА) увеличивается монотонно с увеличением длины трещины, так как смыкания берегов трещины не происходит, а живая часть сечения, воспринимающая нагрузку от распорки, уменьшается. Однако в диапазоне длин трещин от L = 3,5 см (60° окружности образца) до Z = 7 см (120°) шахК, изменятся незначительно (от 130°МПам^1/2 до 180МПам^1/2).

Из сравнения зависимостей, приведенных на рис. 8, а и рис. 8, б видно, что тахА) в случае сонаправленного роста получается большим (maxXi —150 МПам^1/2), чем при противонаправленном росте (тахА) =95 МПам^1/2) во всем диапазоне длин трещин, кроме коротких, у которых L < 1 см. Это объясняется тем, что при противонаправленном росте трещина пересекает область сжатия.

Развитие трещины, определенное теоретически

Хотя расчетное значение maxXi =150 МПа м^1/2 больше вязкости разрушения материала образца К_Ас ⁼ 80 МПа-м^1/2 (напомним, что в вершине трещины температура близка к комнатной), но в тонкостенном образце в вершине трещины реализуется состояние, близкое к плоскому напряженному, и коэффициент интенсивности напряжений в вершине трещины не достигает критической величины К\о = 250 МПа-м^1/2, оцененной по формуле Броека-Влигера [2]. Поэтому рассматриваемые условия отвечают усталостному развитию трещины.

Диаграмма роста усталостной трещины (РУТ) показана на рис. 9. При плоском напряженном состоянии в вершине трещины, которое реализуется в образце, она представлена не только в диапазоне ДК» - АК\_<С (сплошная линия в области I), но расширена до критического значения коэффициента интенсивности напряжений АКуо - штрих-пунктирная линия в области II на рис. 9. Здесь через ДКу_с и AK\jq обозначены такие размахи цикла, когда максимальное значение коэффициента интенсивности напряжений достигает соответственно Ку_с и Куо- Очевидно, что в об-

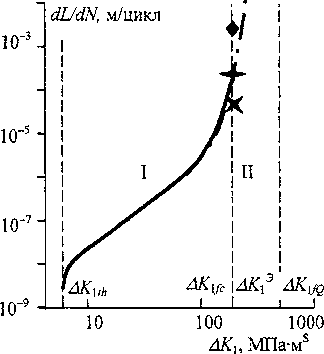
♦ - оценка по размеру зоны разрушения

-^- - экспериментальный результат

X - оценка по раскрытию трещины

Рис. 9. Диаграмма усталостного роста трещины

ласти II скорость роста трещины должна быть существенно выше линии определенная по форму

ле Пэриса и приближаться к бесконечности при приближении к ДКуд.

Осредненное значение действующего размаха коэффициента интенсивности напряжений АК\ = 250 МПа м^/г для диапазона длин трещин от L = 3,5 см (60° окружности образца) до L = 7 см (120°) определено как сумма минимального и максимального значений коэффициента интенсивности в цикле из результатов расчета, представленных на рис. 8.

Размер зоны предразрушения, где напряжения превышают предел прочности, а размах напряжений - удвоенный предел прочности, может быть оценен по выражению [7]

1 ^АХ)

rf =— --L

• ⁷ 2тг ( 2сг_е J

где сгв - предел прочности материала. Результат ту = 2 мм показан на диаграмме РУТ (см. рис. 9) точкой - оценка скорости роста трещины сверху.Оценка скорости РУТ по величине циклического раскрытия трещины [6] дает вторую оценку dL/dN=U?TK/2 = 0,22zlKA2/(2o'yE),                                                       (3)

где ст_у - предел упругости; ЦРТ_К - циклическое раскрытие в зоне кончика трещины. Соответствующая расчетная точка dL/dN = 4Т0^-5 м/цикл показана звездой на рис. 9.

Экспериментально полученный рост трещины и его сопоставление с теоретическим исследованием

В процессе циклического нагружения образцов (были испытаны три образца) начальные трещины распространялись в окружном направлении. В процессе эксперимента проводились замеры длины трещины. Средняя скорость роста одной вершины трещины (у трещины росли обе вершины) за весь период развития dUdN³ = 2-1 О'⁴ м/цикл. Соответствующая точка показана на диаграмме РУТ (см. рис. 9). Экспериментальный результат находится между оценками по формуле (3) и оценкой сверху по (2).

После 103 циклов нагружения трещина достигла длины L = 130 мм, что больше половины окружности образца.

Заключение

Эксплуатация конструкций, подверженных действию высоких тепловых напряжений при незначительных механических, показала возможность их разрушения с образованием длинных трещин. Такое разрушение не может быть объяснено с точки зрения традиционного подхода, не учитывающего движение источников тепла. Движущееся тепловое поле и связанное с ним поле напряжений может приводить к специфическим механизмам роста трещины, которые являются более опасными, чем механизмы, возникающие под действием неподвижных самоуравновешен-ных полей напряжений. Ранее была показана реализация сонаправленного и противонаправленного механизмов на образцах из хрупкого материала (стекла) с образованием длинных трещин.

В настоящей работе исследовано развитие трещин под действием движущихся тепловых полей в малоразмерных лабораторных образцах из пластичного материала. Образцы в форме тонкостенных цилиндрических оболочек, изготовленных из стали, в процессе эксперимента подвергались нагреву в кольцевом индукторе токами высокой частоты. Высокие градиенты температур обеспечивались охлаждением поверхности образца струями воды. Локальное тепловое поле двигалось по окружности в результате вращения образца механическим приводом.

Усталостная трещина в образце в плоскости индуктора, развивалась в окружном направлении со средней скоростью 2-10"⁴ м/цикл, что хорошо согласуется с результатами расчетов. После 103 циклов нагружения длина трещины составила L = 130 мм и превысила половину окружности образца (при этом механическая нагрузка, обусловленная действием распорки в образце, создавала лишь дополнительные напряжения для исключения прогрессирующего обжатия, а рост трещины был обусловлен циклическим нагружением движущимся тепловым полем).

Таким образом, для материала, обладающего значительной вязкостью разрушения, показана возможность усталостного рост трещины в направлении движения теплового поля и в противоположном направлении. Хотя скорость этого роста в сравнении с квазистатическим (сонаправ-ленным или противонаправленным) невелика, трещина может достигнуть значительного размера, который так же, как для квазистатического роста, ограничен лишь областью перемещения зоны теплового растяжения.