Развитие и совершенствование алгоритма одноплоскостной балансировки в динамическом режиме высокоскоростной летающей модели

Введение. Реализация аномальных режимов полёта высокоскоростной осесимметричной летающей модели (ЛМ), например, выполненной в виде стабилизированного вращением вокруг своей геометрической оси длинномерного конического модуля, приводит к снижению точности траекторного движения модели, сбоям и отказам в работе бортовых приборов и систем. Одним из условий движения ЛМ с заданной точностью по расчётной траектории, а также надёжного функционирования бортовой аппаратуры является определение и приведение на завершающем этапе общей сборки параметров её массо-инерционной асимметрии к значениям, не превышающим заданных в эксплуатационной документации предельно допустимых значений. В последнее время наблюдается тенденция к ужесточению требований по точности определения и обеспечения параметров, определяющих асимметрию распределения масс относительно оси симметрии наружной поверхности (или геометрической оси) ЛМ, существенно влияющих на лётнотехнические характеристики модели. К числу параметров массо-инерционной асимметрии относится величина поперечного смещения центра масс с геометрической оси и угол отклонения продольной главной центральной оси симметрии (ГЦОИ) относительно той же оси [1].

Зачастую при проектировании, конструировании и изготовлении высокоскоростной ЛМ стремятся обеспечить симметричность формы корпуса модели и совпадение оси её массовой симметрии с осью симметрии наружной поверхности, которая обычно принимается в качестве строительной. Однако невысокая точность теоретического расчёта параметров массоинерционной асимметрии, как правило проводимого на этапе проектирования, делает актуальной задачу измерения этих параметров [1–3]. Измерения выполняют экспериментальным или расчётно-экспериментальным путём и с применением специализированного контрольно-измерительного оборудования. При этом симметричность формы обусловливает близость к нулю номинальных значений параметров массоинерционной асимметрии, что, в свою очередь, определяет трудности процесса экспериментального определения этих параметров, например, по сравнению с контролем таких массо-центровочных и массоинерционных характеристик (МЦИХ), как масса, продольное положение центра масс, моменты инерции, также определяемых экспериментально после изготовления и сборки модели. Ряд характерных особенностей высокоскоростных ЛМ, таких, в частности, как значительные габаритные размеры, неметаллическая наружная поверхность, наличие нежёстких элементов конструкции, отсутствие удобной технологической базы для закрепления на рабочем органе измерительного стенда, наличие единственной плоскости коррекции, расположенной на значительном расстоянии от центра масс модели, налагают дополнительные ограничения на использование измерительного оборудования и способы выполнения измерений. Процедуру приведения значений параметров массоинерционной асимметрии к заданным нормативам выполняют путём прикрепления корректирующих грузов к штатной плоскости коррекции, как правило конструктивно располагаемой вблизи торца корпуса модели, после её изготовления и сборки.

Для определения массы ЛМ обычно используют стандартные, например, платформенные весы, а определение других МЦИХ выполняют с применением контрольно-измерительных стендов, учитывающих конструктивные и технологические особенности контролируемых объектов и обеспечивающих требуемую точность измерений и безопасность проводимых работ. Координаты центра масс обычно определяют на центровочных стендах, реализующих весовой метод измерений, а для определения моментов инерции используют стенды, реализующие метод физического или крутильного маятника [2–4]. При этом расчёт величины поперечного смещения центра масс и угол перекоса продольной ГЦОИ относительно геометрической оси контролируемой модели выполняют по специальным методикам с использованием результатов измерений МЦИХ. Однако низкая точность стендового оборудования обоих перечисленных типов и малая производительность являются основными факторами, сдерживающими дальнейшее повышение точности определения и обеспечения параметров массоинерционной асимметрии ЛМ.

В работах [4–6] отмечается, что в последнее время для определения параметров массо-инерционной асимметрии высокоскоростных летающих моделей наметилась тенденция к использованию методов и средств динамической балансировки, что обусловлено высокими характеристиками точности динамических балансировочных станков (стендов).

Расчётная схема балансировочного эксперимента. Для прецизионной низкочастотной (рабочая частота вращения не превышает 2 Гц) балансировки осесимметричных ЛМ конической формы в динамическом режиме спроектирована и изготовлена автоматизированная система контроля, построенная на базе вертикального дорезонансного динамического балансировочного стенда с жёсткими опорами, представляющими собой конические газостатические подшипники [7–10]. В качестве рабочего тела используется сжатый воздух, поступающий из заводской пневмосети низкого давления. Контролируемая модель, расчётная схема которой приведена на рис. 1, балансируется на стенде в составе сборного ротора, образуемого собственно ЛМ и специальным защитным технологическим переходником, выполненным в виде усечённого конуса и загружаемого непосредственно на газовые опоры.

Модель устанавливается на внутренние опоры переходника торцом вверх и фиксируется в одном из двух угловых положений относительно переходника, отличающихся друг от друга на 180º [4; 11]. Применение переходника обеспечивает материализацию второй (нижней, обозначаемой символом «Н») плоскости коррекции и необходимо для настройки измерительной системы стенда и проведения балансировочного расчёта. При этом в качестве первой (верхней, обозначаемой символом «В») плоскости коррекции используется штатная плоскость коррекции ЛМ. В процессе балансировочного эксперимента выполняют серию пусков сборного ротора как с пробными грузами, установленными в плоскостях коррекции, так и с ЛМ, установленной внутри технологического переходника в исходном положении. Измерения в исходном состоянии выполняют дважды для двух взаимно противоположных угловых положений ЛМ относительно технологического переходника с последующим усреднением результатов измерений, что позволяет исключить влияния собственных дисбалансов переходника на результаты измерений [11; 12]. В каждом пуске определяют амплитуды и фазы вибраций газовых опор на рабочей частоте вращения сборного ротора. При этом обработку измерительных сигналов выполняют с использованием комбинированного аналого-цифрового фильтра [13; 14].

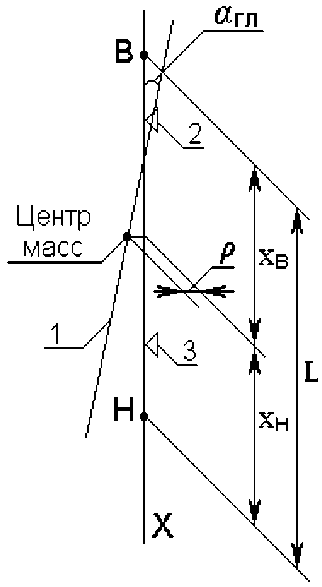
Рис. 1. Расчётная схема:

1 – продольная ГЦОИ; 2 и 3 – соответственно верхняя и нижняя опоры, выполненные в виде конических газостатических подшипников

По результатам измерений вибраций опор в пусках с пробными грузами рассчитывают коэффициенты чувствительности измерительной системы к дисбалансам и коэффициенты взаимовлияния плоскостей коррекции [15]. С использованием указанных коэффициентов, по результатам измерений вибраций опор в пусках сборного ротора с ЛМ, находящейся в исходном положении, определяют векторные параметры (значения и углы) начальных дисбалансов D B и D _Н , действующих соответственно в верхней и нижней плоскостях коррекции, и рассчитывают начальные параметры радиуса-вектора р поперечного смещения центра масс и вектор-угла а _ГЛ перекоса продольной

ГЦОИ модели относительно её геометрической оси по формулам [4; 11]

—*        —*

р - D В ⁺ D И ;

М

——            ——

DВ x В - DИ x И агп - — arcsin---------------

ГЛ эа где М – масса ЛМ; I и I – соответственно её эква-эа ториальный и аксиальный моменты инерции.

Применение метода динамической балансировки позволило достигнуть погрешностей определения указанных параметров массо-инерционной асимметрии, не превышающих соответственно 0,01 мм и 1 угловой минуты, что в 5–6 и более раз превышает погрешности определения тех же параметров на стендах, реализующих методы статической балансировки.

В случае если начальное значение хотя бы одного из параметров, характеризующих асимметричность в распределении масс ЛМ, превышает соответствующее предельно допустимое значение, заданное в эксплуатационной документации на модель, выполняют корректировку её массы. При этом использование коэффициентов взаимовлияния плоскостей коррекции позволяет расчётным путём определить массу и угловое положение балансировочного груза для его прикрепления к штатной плоскости коррекции модели либо показать невозможность обеспечения одновременно двух контролируемых параметров массо-инерционной асимметрии по заданным нормативам (в этом случае балансировка завершается, а модель направляется на перекомпоновку). Следует отметить, что балансировочный расчёт может быть проведён с оптимизацией по критерию достижения минимального значения любого из параметров без выполнения дополнительных шагов балансировки. Учитывая, что на практике балансировщики стремятся достичь минимального значения поперечного смещения центра масс, обеспечивая при этом допустимое по документации на модель значение угла перекоса продольной ГЦОИ, рассмотрим вариант балансировочного расчёта с оптимизацией параметров по критерию достижения минимального поперечного смещения центра масс.

Алгоритм обеспечения параметров асимметрии масс. Сначала ЛМ расчётным путём приводят к режиму квазистатической неуравновешенности, когда её геометрическая ось и продольная ГЦОИ пересекаются не в центре масс, для чего с учётом взаимовлияния плоскостей коррекции моделируют устранение действия начального дисбаланса в штатной (верхней) плоскости коррекции введением в этой плоскости равного ему по значению, но противоположного по направлению компенсирующего дисбаланса DBКОМП [6]. Эта процедура позволяет упростить последующие вычисления и перейти при расчётах коллинеарных векторов дисбалансов к операциям с одномерными величинами. Затем с учётом взаимовлияния плоскостей коррекции моделируют введение в штатной плоскости коррекции корректирующего дисбаланса DBКОРР , равного по значению, но противоположного по направлению дисбалансу DНКОМП , сформировавшемуся в нижней плоскости коррекции в результате предыдущего шага моделирования. Это позволяет устранить поперечное смещение центра масс с геометрической оси и виртуально перевести ЛМ в режим моментной неуравновешенности, когда геометрическая ось и продольная ГЦОИ пересекаются в центре масс. Оценивают угол перекоса продольной ГЦОИ относительно геометрической оси ЛМ, который будет предположительно образован в результате моделирования компенсирующего и корректирующего дисбалансов, по формуле

КОРР аГЛ

1      2 D КОРР L

= — arcsin —В----

I э - I

эксперимент прекращают, а контролируемую модель бракуют и направляют на перекомпоновку. В ином случае определяют значение вектора дисбаланса D _В ^К _м ^О _и ^Р _н ^Р , сонаправленного вектору D _В ^КОРР и обеспечивающего достижение минимально возможного смещения центра масс для варианта, когда угол перекоса продольной ГЦОИ равен а _ГЛдоп , по формуле

( i — i ) '"-2-     — d ^komh

D КОРР = D КОМП + "-------- ²------------ К в - I.

Вмин Н                                           НВ .

x B ⁺ K HB ■ ^Х Н

где L = х В + х _Н - соответственно расстояние между

верхней и нижней плоскостями коррекции; D _В ^КОРР –

значение дисбаланса, смоделированного в верхней плоскости коррекции, для перевода контролируемой модели в состояние моментной неуравновешенности с учётом взаимовлияния плоскостей коррекции.

Затем определяют значение и угол балансировочного вектора по формулам

БАЛ КОМП2 КОРР2

D Вмин = V ^D B     ⁺ D Вмин ⁺

+_л / 2 D К^ОМП D КОРР cos (а К^ОМП В Вмин       В

КОРР аВмин )

В случае если значение а КОРР не превышения

предельно допустимого значения данного параметра а _ГЛдоп , то значение и угол балансировочного вектора D _В ^БАЛ рассчитывают как геометрическую сумму компенсирующего и корректирующего дисбалансов в верхней плоскости коррекции по формулам

БАЛ аВмин

= arctg

sin а

КОМП В

cos а

КОМП В

+ sin а

КОРР Вмин

+ cos а

КОРР , Вмин

> БАЛ = 4 d К^ОМП2 + d К^ОРР2 + BB В

КОМП КОРР      КОМП КОРР

+./2 D в     D в   cos ( а В -а в ) ;

а ВАЛ

= arctg

sin а

КОМП В

+ sin а

КОРР В

где а КОРР - угловое положение дисбаланса D ВКОРР . После чего по законам статики рассчитывают массу и угловое положение балансировочного груза и корректируют массу ЛМ.

На рис. 2 показаны расчётные дисбалансы, действующие в плоскостях коррекции в процессе и по окончании приведения значений параметров массо-инерционной асимметрии ротора к значениям, не превышающим заданных предельно допустимых значений.

cos а

КОМП В

+ cos а

КОРР , В

где а К^ОМП - угловое положение дисбаланса D ВКОМП ; а К^ОРР — угловое положение дисбаланса D К^ОРР . А затем по законам статики рассчитывают массу и угол установки балансировочного груза в штатной плоскости коррекции и корректируют массу ЛМ. В противном случае рассчитывают предполагаемое (одновременно являющееся минимально возможным для данного варианта компоновки контролируемой модели) значение поперечного смещения центра масс, задавая значение угла перекоса продольной ГЦОИ равным предельно допустимому значению, по формуле

КОМП

D _H

( i э - 1 _а) ^"’22

^Р мин

х В ⁺ K НВ х Н

КОМП

D _Н   х _Н

( КНВ - 1)

М

,

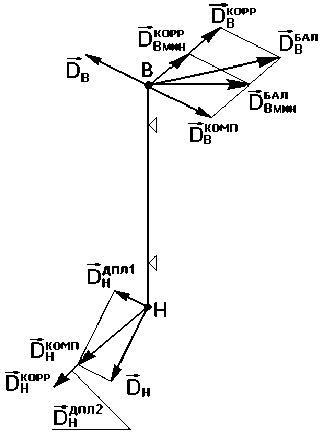
Рис. 2. Диаграмма балансировочного расчёта

где K _НВ – коэффициент влияния верхней (штатной)

плоскости коррекции на нижнюю плоскость коррекции при наличии дисбаланса в верхней плоскости коррекции; D _Н ^КОМП – значение дисбаланса, действующего в нижней плоскости коррекции, после компенсации начального дисбаланса, действующего в верхней плоскости коррекции. Далее, в случае если значение р _мин будет превышать предельно допустимое значение параметра р _доп, то балансировочный

При проведении расчёта дополнительные дисбалансы D H^ДПЛ1 , D H^ДПЛ2 и D H^ДПЛ3 (не показан), появляющиеся в нижней плоскости коррекции в результате влияния на неё верхней плоскости коррекции, при формировании в ней соответствующих компенсирующего и корректирующих дисбалансов, вычисляют по формулам

D ДПЛ1 ₌ D КОМП К ; HBНВ

D ДПЛ2 ₌ D КОРР НВ

ДПЛ3    КОРР

D Н ⁼ D Вмин

К НВ ;

К НВ .

Заключение. Рассмотренный алгоритм обеспечивает прецизионное приведение одновременно двух контролируемых параметров массо-инерционной асимметрии к значениям, не превышающим соответствующих предельно допустимых значений, с оптимизацией по критерию достижения минимального смещения центра масс с геометрической оси модели. При этом сокращается число шагов балансировки и время балансировочного эксперимента. Точность приведения контролируемых параметров асимметрии к заданным нормативам обеспечивается точностью измерений сигналов дисбалансов [13], а также точностью вычисления массы и углового положения балансировочного груза в ходе балансировочного расчёта. Алгоритм и способ балансировки роторного объекта в единственной плоскости коррекции, расположенной на значительном расстоянии от центра масс объекта контроля, защищён патентом РФ на изобретение [16]. Экспериментальное опробование расчётного алгоритма и способа балансировки, проведённого на вертикальном балансировочном стенде с опорами, выполненными в виде конических газостатических подшипников, подтвердило его высокую точность и эффективность.