Развитие эллипсометрии

Эллипсометрия за последнее десятилетие претерпевает период интенсивного развития и существенного расширения области применения. Это прежде всего связано с высокой чувствительностью метода к состоянию поверхности, точностью измерения толщин пленок вплоть до долей ангстрема и важным достоинством — неразрушающим и невозмущающим характером измерений и возможностью проведения исследований не только in situ, но и in vivo. Особенно интенсивно развиваются приложения метода в нанотехнологии и молекулярно-лучевой эпитаксии. В ряде случаев это оказывается практически единственный методом, позволяющим осуществлять неразрушающий контроль в процессе синтеза структур, отвечающим все возрастающим требованиям к точности и информативности контроля и управления технологическим процессом. Интенсивно развиваются приложения метода в областях медицины, биологии и экологии созданием высокочувствительных сенсоров и анализаторов (метод плазмонного резонанса, реакции антиген—антитело и т.п.).

СТОКС-ЭЛЛИПСОМЕТР

Фактически первый отечественный автоматический эллипсометр, пригодный к серийному производству, был разработан в 1990 г. в виде приставки к ручному эллипсометру ЛЭФ3М-1, выпускавшемуся Феодосийским приборостроительным заводом. Простая для таких приборов конструкция приставки и новый теоретический подход позволили получить высокие показатели, заметно превосходящие зарубежные аналоги, при весьма низких ценах. Следует заметить, что за рубежом впервые стокс-эллипсометр фирмы Gaertner (в серийном исполнении) появился на 3 года позже, и цена его составляла $98 000. В настоящее время приставка несколько модернизирована и подключается к компьютеру через USB-разъем.

Принципиальная схема эллипсометра допуска- ет сочетание в одном приборе "нулевого" и фотометрического подходов. Базовый эллипсометр ЛЭФ3М-1 был естественным образом (без конструктивных изменений) дополнен приставкой, позволяющей осуществить автоматизированный измерительный процесс стокс-параметров по фотометрической схеме. Оптическая схема комбинированного прибора приведена на рис. 1.

Схема ручного эллипсометра содержит источник света J — He-Ne лазер, поляризатор P, компенсатор C и анализатор A, установленные в лимбы с ручным приводом и шкалами отсчета; переключатель направления светового потока в виде поворотного зеркала З и фотоприемник ФЭУ с усилителем и индикацией уровня сигнала (на схеме не показаны). Автоматизация измерений осуществляется за счет установки модулятора поляризации M и фотометрического блока ФД. Управление модулятором и цифровая обработка сигнала осуществляются посредством платы контроллера, подключаемого к компьютеру через USB-разъем (на схеме не показаны). Пакет программного обеспечения осуществляет все необходимые функции по управлению измерением и обработке данных.

В режиме автоматических измерений (положение элементов в позиции 1) отраженное от образца S излучение модулируется модулятором M и, пройдя анализатор, попадает на фотоприемник ФД. Результатом измерения является полный вектор Стокса отраженного излучения [1].

В режиме ручного измерения (положение элементов в позиции 2) модулятор M выводится из оптического тракта, а сигнал попадает на фотоприемник ФЭУ. Таким образом, прибор работает по стандартной схеме нуль-эллипсометра.

Кроме очевидных преимуществ автоматизации измерений и более высокой точности по сравнению с зарубежными аналогами, стокс-эллипсометрия содержит больше информации об измеряемом объекте. Четыре параметра Стокса, кроме чисто поляризационных параметров, содержат также информацию о деполяризующих свойствах

ФЭУ

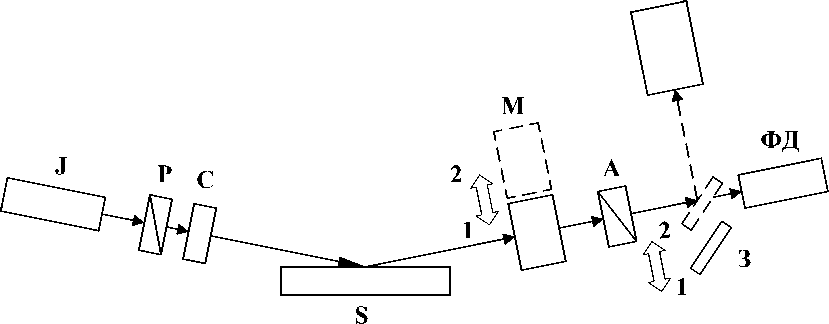
Рис.1. Оптическая схема комбинированного эллипсометра

образца и амплитудных коэффициентах отражения [1]. Модели реальной поверхности с учетом неоднородности и деполяризации более естественно и ясно формулируются в терминах стокс-векторов и матриц Мюллера. Нуль-эллипсометрия в этом случае дает лишь некоторые эффективные значения Ψ и ∆ , которые трудно однозначно интерпретировать. Таким образом, можно сказать, что стокс- и нуль-эллипсометрия измеряют несколько различные параметры исследуемых объектов. Совпадение значений Ψ и ∆ , вычисленных из результатов стокс-измерений, и измерений в режиме нуль-эллипсометрии должно наблюдаться только для поверхности и пленок, близких к идеально планарным, с малой дисперсией в пределах измеряемого спектра и при строго параллельном пучке света.

Комбинированная схема позволяет также оптимизировать измерения для каждого образца. Это достигается путем выбора оптимального состояния поляризации падающего излучения посредством установки соответствующих положений P и C.

В полуавтоматическом режиме возможно полное измерение анизотропии. Для этого проводятся четыре измерения при четырех комбинациях (P, C) i ( i = 1, 2, 3, 4), что дает возможность определить полную матрицу Мюллера исследуемой системы.

Принципиальной и важнейшей особенностью такого измерительного комплекса является возможность его метрологического самотестирования и проверки посредством измерения одного и того же объекта разными способами.

МИНИ-СТОКС-ЭЛЛИПСОМЕТР

Разработан новый для данной области тип прибора — малогабаритный cтокс-эллипсометр, который не уступает по метрологическим характеристикам стационарным приборам, но имеет габариты не более 140 × 80 × 70 мм. Для данной области это является поворотным этапом развития, т. к. позволяет использовать данный метод не только в лабораторных условиях и высокотехнологичных производствах, но и в мобильных лабораториях, клиниках, в системах экологического мониторинга как сверхчувствительный датчик или анализатор различных веществ (на основе плазмонного резонанса и химически селективных пленок). Это существенно расширяет области применения данного метода. Данный прибор обладает весьма высокими метрологическими возможностями и при неизменной базовой конструкции может быть легко модифицирован под конкретные технологические и исследовательские задачи. Например, могут быть добавлены еще несколько измерительных каналов с разными длинами волн или направлений измерения, что позволяет за одно измерение определять полные характеристики анизотропии пленки или подложки (ориентацию и величины компонент тензора диэлектрической проницаемости). Добавление многоканального спектрофотометра на ПЗС-линейках и световодных элементов вво-да/вывода дает возможность измерения спектральных характеристик анизотропии за то же время. Вследствие малых габаритов, веса и осо- бенностей конструкции (весь прибор находится выше плоскости образца) мини-эллипсометр идеально подходит для задач сканирования крупногабаритных деталей, например плоских мониторов, кремниевых пластин диаметром 300 мм и более, покрытий крупногабаритной оптики и т. п., т. к. вместо перемещения самой детали, что применяется в зарубежных аналогах (SOPRA, Gaertner), гораздо проще перемещать измерительный прибор.

ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ

Программное обеспечение и методы обработки сигнала также подверглись существенным изменениям. Кроме общего развития вычислительных процедур, улучшения интерфейса, расширения и уточнения различных моделей поверхностных структур и процессов, особо следует отметить существенное продвижение в области собственно измерительного процесса, оптимальной оценки измеряемых параметров, фильтрации шумов и учета полной информации о погрешности измеряемых параметров, включая и свойства корреляции в виде ковариационных матриц.

Существенной особенностью эллипсометрии является значительная зависимость погрешности измерений от свойств измеряемого объекта. Например, при прочих равных условиях погрешность эллипсометрических параметров Ψ и Δ может увеличиваться на несколько порядков при стремлении Ψ к нулю; погрешность измерения толщины пленки резко увеличивается, если показатель преломления ее приближается к показателю преломления подложки. Кроме того, как сами параметры Ψ и Δ или компоненты вектора Стокса, так и вычисляемые по ним параметры пленок и поверхностных структур оказываются сильно коррелированными. До настоящего времени при вычислении значений параметров погрешности не учитывались, а определялись по статистической обработке при многократных измерениях. Полное изложение вопроса предполагается в дальнейших публикациях. Здесь мы кратко коснемся только некоторых результатов.

Рассмотрим фотометрический эллипсометр, содержащий источник света, поляризатор и/или модулятор поляризации, измеряемый образец, анализатор и/или модулятор поляризации и фотоприемник. Предполагается, что оптическая система линейна, и все ее компоненты (кроме исследуемого образца) — недеполяризующие, т. е. модуляторы и поляризаторы описываются с помощью формализма матриц Джонса. Модуляторы могут находиться как в одном из плеч, так и в обоих одновременно. Модуляция имеет периодический характер с периодом T. В этих предполо- жениях в силу линейности любая система может быть представлена в виде

J ( t ) =

= J 0 • ( m 1 ( t ) • x 1 + ... + m 4 ( t ) • x ₄),        (1)

где J ₀ — интенсивность источника света (полагаем, что J 0 — приведенное значение, учитывающее потери света на оптических элементах), x_i — компоненты вектора отражения X , m_i ( t )— коэффициенты модуляции, зависящие от времени, и J ( t )— интенсивность света на фотоприемнике. Если определить еще вектор модуляции системы M ^T( t )

M T⁽ t ) = ( m 1 ⁽ t ), m 2 ⁽ t ), m 3 ⁽ t ), m 4 ⁽ t ) )          ⁽²⁾

то интенсивность на фотоприемнике может быть представлена в виде скалярного произведения

J ( t ) = J 0 • M ^T( t ) • X .                  (3)

Конкретный вид компонент вектора модуляции однозначно определяется конструкцией прибора. Например, для системы P R SA — вращающийся поляризатор ( P = to t ), образец S, анализатор A , измеряются только три компоненты X ^T = ( R p У ^Re( R p R * )^, ^ R_s ² ^) — компоненты вектора модуляции для идеальных элементов имеют вид

MT (t) = 1 (cos2 A[1 + cos(2P)], sin(2A) sin(2P), sin2 A[1 - cos(2P)]). (4)

Если вектор X не зависит от времени, то система, состоящая из оптической части плюс измерительный тракт, может быть представлена в виде

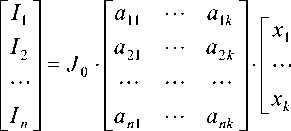
где a.

^a ij

т

- ( i + 1)

n

J m j ( t )d t ,

T

i

n или в компактной форме

I = AX .                    (6)

Здесь n — число измерений (используемых функционалов) за период T , k — размерность измеряемого вектора X , I — вектор измеренных значений, A — матрица прибора. Очевидно, что должно быть n >  k . Матрица A , или ее можно назвать "прямой" матрицей прибора (в статистике "конструкционная" матрица), — это полная характеристика данной системы, и все систематические погрешности и несовершенства оптических элементов имеют значение только относительно влияния на компоненты этой матрицы. В силу линейности соотношений решение системы может быть выражено также в виде линейного уравнения

X = BI , (7)

где B мы называем "обратной" матрицей прибора. Очевидно, что если n = k и матрица A неособенная, то решением является

B = A - 1 . (8)

Если n >  k , то матрица B может быть определена в общем случае неоднозначно. Именно избыточность числа измерений n по сравнению с размерностью вектора X и позволяет оптимизировать процесс обработки сигнала.

Подходящим аппаратом для решения подобных задач является обобщенный метод наименьших квадратов ОМНК [7]. Если известна ковариационная матрица ошибок D ( I ) для измеренных значений вектора I , то задача минимизации погрешностей вектора X в уравнении (7) имеет, согласно [7], аналитическое решение в виде

B = ( A ^t D(I) - 1 A ) - 1 A ^T D(I) - 1 , (9)

D(X) = (A ^T D(I) - 1 A) - 1 . (10)

Здесь D(X) — ковариационная матрица ошибок измеряемого вектора X . Из уравнения (9) очевидно, что обратная матрица B в общем случае не является постоянной, а зависит от измеряемых параметров.

Для примера рассмотрим частный случай дробового шума. Дробовой шум характеризуется распределением Пуассона, основное свойство которого заключается в том, что дисперсия пропорциональна интенсивности сигнала, и последовательные измерения можно считать статистически независимыми. Следовательно, ковариационная матрица D ( I ) имеет диагональный вид с элементами диагонали, пропорциональными измеренным интенсивностям. Коэффициент пропорциональности можно определить, используя подход, примененный в [4–6]. В принятых здесь обозначениях матрица имеет вид

I 1

D ( I ) sh = K ² hv

I ₂

I n

h — постоянная Планка, ν — частота света, K — коэффициент усиления измерительного тракта (если измерение ведется в режиме счета фотонов, т. е. I i — сумма зарегистрированных частиц, то K = 1).

Если дробовой шум является определяющим, то, подставив выражение (11) в (9) и (10), а также в (7), можно получить следующие соотношения:

D(X)sh =[A t D(I)-1 A ]-1,(12)

X = D(X)sh С,(13)

T

С = A Т D(I)s—h11 = П_ Jm( t )d t,(14)

Khv *

где η — квантовая эффективность фотоприемника.

Вектор C не зависит от измеренных значений и не зависит от числа разбиений n . Он является характеристикой прибора, определяющей величину погрешностей измеряемого вектора X для одного измерительного цикла. Если измерения усредняются за N циклов, то соответственно C ( N) = N С Например, для системы с вращающимся поляризатором

^C ' rotP = -^^T [ cos² A, ⁰ , sin² A ^] . ⁽¹⁵⁾ rotP _Kh v ₂

Уравнения (12) и (13) позволяют вычислять наилучшую оценку X и ее доверительную область, определяемую ковариационной матрицей R ( X ).

Формула (13) является обобщением закономерностей пуассоновского распределения на многопараметрические и нестационарные процессы. В частности, формула Шоттки может быть получена как частный случай этого выражения ( k = 1, M ( t ) = const).

Для количественного сравнения рассмотрим обработку измерений с помощью "Hadamard summation", применяемого в приборах фирмы Sopra, и предлагаемый подход. Метод "Hadamard summation" [8] в данных обозначениях математически эквивалентен применению фиксированной обратной матрицы B и числу разбиений n = 4. На рис. 2 приведено семейство графиков отношения площадей доверительных областей в зависимости от числа разбиений n периода модуляции T . Из графиков видно, что данный метод позволяет значительно повысить точность измерений — на порядок

Отношение площадей, S 1 / S 2

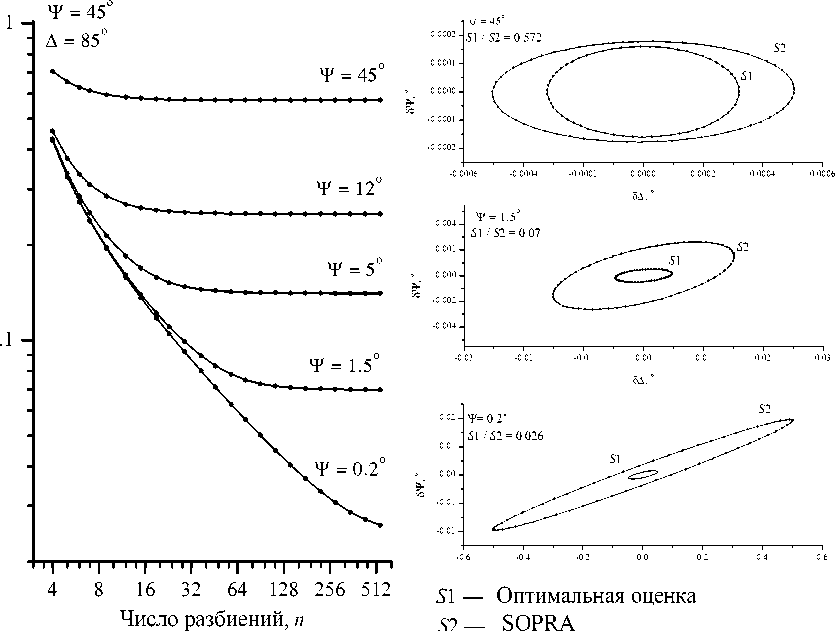
Рис

. 2. Сравнительные размеры и ориентации доверительных областей для различных значений Ψ и числа разбиений n

а

Рис. 3. Сравнительные размеры доверительных областей вектора Х для белого шума (Ψ = 2.5°, Δ = 175°; оптимальная оценка и SOPRA).(а, б — виды с разных позиций одного объекта)

и более и что следует стремиться к наибольшей скорости обработки сигнала для увеличения числа отсчетов за период модуляции. Следует также заметить, что малые значения Ψ соответствуют углу Брюстера, при котором достигается наибольшая точность определения параметров тонких пленок.

Для белого шума, характерного при применении лазерных источников, результаты оказываются еще более впечатляющими. На рис. 3 приведены трехмерные доверительные области для векторов Стокса. Так как разница в размерах составляет около двух порядков, область оптимальной фильтрации видна как черточка внутри эллипсоида, соответствующего обычным расчетам.

На рис. 4 представлены доверительные области Ψ и Δ, соответствующие данным, представленным на рис. 3. Область фильтрации видна как маленькая черточка, т. к. размеры областей отличаются более чем на три порядка.

ВЫВОДЫ

Новые технические и теоретические решения позволяют существенно повысить эффективность и точность эллипсометрических приборов, расширить область их применений и, возможно, получить новые результаты в области фундаментальных исследований. Предлагаемый метод оптимизации и оценки погрешности является универсальным, применим практически к любым фотометрическим системам поляриметрии и эллипсометрии, дает надежную основу для метрологического сравнения и оптимизации различных систем.

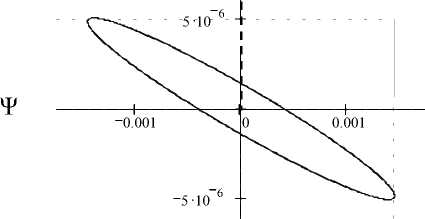
Δ

Рис. 4. Сравнительные размеры доверительных областей Ψ и Δ для белого шума (оптимальная оценка и SOPRA)

• 4.    Aspnes D.E. // J. Appl. Opt. 1975. V.14, N 5. P. 1131–1136.

• 5.    Aspnes D.E. Optical Properties of Solids New Developments / Ed. B.O. Seraphin. North Holland, Amsterdam, 1976. 799 p.

• 6.    Aspnes D.E. // J. Opt. Soc. Am. 1974. N 64. P. 639.

• 7.    Hamilton W. Statistics in physical science. N.Y., 1964. 430 p.

• 8.    Courdille M., Steers M. and Theeten J. B. Patent FR 2491234 (29 September, 1980).