Развитие метакогнитивных способностей в условиях перехода на новые образовательные стандарты

Введение в школьную практику государственных образовательных стандартов нового поколения на законодательном уровне закрепило переход от «знаниевой» парадигмы в обучении к компетентностной. Образование с этих позиций – это формирование опыта решения проблем на базе имеющегося в культуре и социуме опыта, осмысление собственного опыта, преобразование знаний и умений в ресурс для поиска решения новых задач, ранее неизвестных. Переход к новой парадигме требует изменения приоритетов в организации процесса обучения, что и закреплено в государственном образовательном стандарте начального образования. В ФГОС записано: «…выпускник начальной школы должен овладеть основами умения учиться, уметь организовывать свою деятельность» [5; 7]. Поэтому в системе универсальных учебных действий выделены регулятивные учебные действия (целеполагание, планирование, прогнозирование, контроль и др.). Именно они способствуют становлению ученика как субъекта учебной деятельности.

Наши наблюдения, анализ литературы показывают, что при всем старании учителей большинство младших школьников в настоящее время не становятся субъектами учебной деятельности. Многие из них даже с помощью учителя не могут сформулировать учебную задачу, спланировать и определить способы ее достижения, оценить успешность решения учебной задачи и т. д. Специфика данных учебных действий заключается в том, что они более высокого порядка, чем общеучебные и предметные умения (умение читать, наблюдать, считать и др.). Эти учебные действия не могут формироваться по-операционно, как принято в традиционном обучении, необходимо искать иные способы решения проблемы.

Одновременно психологами разрабатывается концепция метапознания, основоположником которой является Дж. Флейвелл. Он определяет метапознание как индивидуальное знание, касающееся собственных когнитивных процессов и их результатов, выполняющее функцию активного контроля, регуляции и организации когнитивных процессов при достижении конкретных целей [6].

Наряду с термином «метапознание» в русскоязычной и иностранной литературе используются также термины «метакогнитивные способности», «метаспособности», «метакогниции» и др. В своей работе мы будем использовать данные термины как синонимы.

Определяя функции метакогниций, Дж. Флейвелл указывает на то, что они выполняют функцию контроля и регуляции когнитивных процессов. Психологами выделены ситуации, которые актуализируют метакогнитивные способности: новизна познавательной ситуации; сосредоточенность на собственной мыслительной деятельности; наличие существенных рассогласований в деятельности; наличие достаточно большого количества времени на решение задачи и др. [2]. Из вышесказанного следует, что развитие мета-когнитивных способностей тесно связано с формированием регулятивных учебных действий, они влияют друг на друга. Наиболее полно эта связь проявляется при постановке и решении учебных задач.

В литературе (И. А. Зимняя, Л. М. Фридман и др.) под учебной задачей понимается задача, в ходе решения которой ученик не только усваивает общий способ выполнения действия, но и происходят изменения в ученике как субъекте учебной деятельности.

С нашей точки зрения, это психологическое понятие должно быть уточнено. Данных характеристик для отличия учебных задач от других, например решаемых в математике конкретнопрактических задач, недостаточно. В. В. Давыдов [1] специально акцентирует внимание на том, что освоение обобщенных способов само по себе не гарантирует изменение субъекта. Овладение способом действия расширяет возможности ученика как решателя задач. Поэтому учебная задача связана не просто с усвоением обобщенных способов действий, а с усвоением теоретических оснований, на которых строятся способы действий, то есть с усвоением принципов действий. Принцип дает возможность человеку строить целые серии действий. «Принцип человек не может усвоить через показ, тренировку. Его нужно извлечь из способов и обобщить» [3; 20]. Таким образом, речь идет о перестройке старых знаний и умений, в результате которой появляется новое целостное образование, новая способность.

Кроме того, цель субъекта, решающего учебную задачу, состоит не только в получении определенного вещественного или идеального продукта и в овладении способом его получения, но и в присвоении этого способа. Тем самым происходит расширение и обогащение возможностей школьника как субъекта учебной деятельности. Но из рассуждений психологов трудно понять, кто ставит цель по усвоению принципа действия: учитель или ученик. Наш опыт экспериментальной работы убедил, что для присвоения выделенного общего способа действия очень важно, чтобы эта цель была поставлена самим учеником. Только в таком случае ученик становится активным участником процесса поиска решения учебной задачи, тогда процесс усвоения знания становится целостным. Поэтому под учебной задачей мы понимаем задачу, которую поставил ученик для себя сам и которая направлена на поиск общего принципа выполнения действия.

Если уточнить схему постановки и решения учебной задачи, предложенную в работе [4], с точки зрения развития метакогнитивных способностей, то получим следующую граф-схему (см. рисунок).

Исходя из этой схемы можно выделить этапы организации обучения на основе развития мета-когнитивных способностей школьников.

• 1.    Постановка учебной задачи: мотивировка → выяснение противоречия (имеется некоторая проблема – способ ее разрешения неясен) → выявление границы знания и незнания → учебная задача.

• 2.    Планирование поиска и решения учебной задачи: анализ имеющихся ресурсов (знания и умения, имеющиеся модели, способы получения дополнительной информации и др.) → выявление общего способа решения задачи и его обоснование (использование разного рода моделей, образов, логических умозаключений) → составление плана решения задачи.

• 3.    Реализация плана решения: применение найденного способа решения при решении задач, аналогичных исходной конкретно-практической задаче → применение найденного способа в измененной ситуации → прогнозирование возможных ошибок → выявление ситуаций, позволяющих изменить способ решения, и т. д.

• 4.    Контроль и оценка решения учебной задачи: установление соответствия полученного результата требованию задачи → коррекция выявленного способа → выделение границ применимости способа → постановка новой учебной задачи.

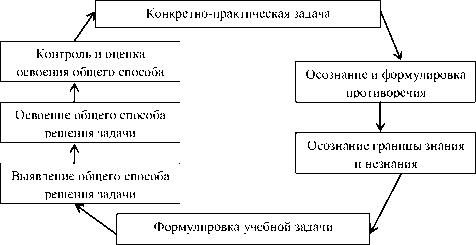
Процесс постановки и решения учебной задачи с позиций развития метакогнитивных способностей

При наполнении этой схемы содержанием, соответствующим учебному предмету, можно получить методику изучения конкретного учебного материала. Мы опробовали эту схему при формировании вычислительных навыков, в частности при изучении устных приемов сложения и вычитания двузначных чисел во втором классе. Такой выбор обусловлен разными причинами, мы отметим наиболее важные с точки зрения развития метакогнитивных способностей:

• 1.    Именно при выполнении устных вычислений ученик должен активно регулировать свои когнитивные процессы: выбрать способ вычисления, проверить себя, если необходимо, скорректировать процесс вычисления и т. д., что способствует формированию регулятивных учебных действий.

• 2.    Слабое владение техникой устных вычислений мешает ученику в усвоении математики, физики, химии в старших классах, где достаточно часто требуется быстро «прикинуть» или оценить возможный результат.

• 3.    Формирование вычислительного навыка вроде бы старая проблема и трудно найти что-то новое в методике, но тем не менее до сих пор

это головная боль многих учителей. Поэтому нужно искать новые и новые способы обучения. Видимо, работа только над вычислительным навыком не является способом решения проблемы. Необходимо использовать другие ресурсы, в том числе и обучение на основе развития метакогни-тивных способностей.

Традиционно учеников второго класса учат последовательному сложению чисел. Например:

• 1)    57 + 22 = (57 + 20) + 2 = 79;

• 2)    57 + 9 = (57 + 3) + 6 = 66;

• 3)    57 + 29 = (57 + 20) + 9 = (77 + 3) + 6 = 86.

Если в первом случае хорошо видны слагаемые, которые нужно прибавить к первому слагаемому, то во втором случае требуется дополнительная операция по разбиению второго слагаемого на удобные слагаемые 3 и 6, причем ее нужно выполнить в уме. А в третьем случае нужно выполнить уже комбинацию преобразований в уме. Все это вызывает сложности у второклассников в связи с малым для выполнения таких преобразований объемом памяти и внимания.

В то же время существуют другие приемы устных вычислений, сокращающие количество шагов. Опыт показал, что они вызывают интерес у учащихся. Например:

• 1)    в случае 57 + 9 нужно просто цифру десятков увеличить на 1, а цифру единиц уменьшить на 1, получим 66;

• 2)    в случае 57 + 29 нужно цифру десятков увеличить на 3, а цифру единиц уменьшить на 1, получим 86.

Использование разных приемов вычислений требует не только математических знаний и умения их применять в конкретных ситуациях, но и умений, которые связаны с метакогни-тивными способностями, с регулированием вычислительной деятельности.

Поэтому на основе высказанной выше идеи нами была разработана методика обучения устным вычислениям, решающая проблемы предметного характера (сокращение количества шагов в вычислении, количества запоминаемого материала и др.) и способствующая достижению метапредметных результатов. Рамки статьи не позволяют описать данную методику. Представим результаты ее применения.

В начале и конце опытно-экспериментальной работы были предложены задания, с помощью которых мы выявляли правильность и обобщенность вычислительного навыка. Нас также интересовала работа второклассников на этапе мотивировки и постановки учебной задачи: смогут ли ученики сформулировать проблему, сформулировать учебную задачу? Ответы на эти вопросы мы фиксировали в ходе наблюдения за школьниками. Полученные данные представлены в таблице.

Сформированность вычислительного навыка

Класс	Правильность		Обобщенность		Формулировка проблемы и учебной задачи
	до обучения	после обучения	до обучения	после обучения	до обучения	после обучения
ЭК (30 уч.)	36,7 %	73,4 %	33,3 %	83,3 %	1 ученик	8 учеников
КК (33 уч.)	22,7 %	52,4 %	36,2 %	38 %	–	1 ученик

Анализ данных показывает, что в обоих классах значительно возросла правильность вычислений. В экспериментальном классе также значительно выросла обобщенность, в том и другом классе некоторые дети стали видеть проблему и пытаться ее формулировать, формулировать учебную задачу.

Для оценки достоверности различий между процентными долями, полученными в контрольном и экспериментальном классах, мы использовали критерий ϕ * – угловое преобразование Фишера. Вычисления показали:

• •    различие в процентных долях учащихся, правильно выполнивших вычисления в экспериментальной и контрольной группах, незначимо (p ≤ 0,01);

• •    различия в процентных долях учащихся, обобщающих вычислительный прием на новые случаи вычисления, в экспериментальной и контрольной группах значимо (p ≤ 0,01).

Полученные данные позволяют сделать вывод: в экспериментальных классах при обучении рациональным приемам вычислений на основе обучения, способствующего не только формированию конкретных учебных умений, но и развитию метакогнитивных способностей, происходят качественные изменения в овладении вычислительными навыками.

DEVELOPMENT OF METACOGNITIVE SKILLS DURING TRANSITION TO NEW EDUCATIONAL STANDARDS