Развитие практического мышления и повышение мотивации к обучению студентов вузов при реализации дистанционных динамических расчетных проектов по математике

В настоящее время применение различных видов информационнокоммуникационных технологий [1-3] в процессе обучения математике является актуальным в силу необходимости комплексного решения реальных дидактических, методических, математических и информационных задач, направленных на повышение интереса и мотивации учащихся к учебной и научно-исследовательской деятельности, а также формирование и последующее развитие практического мышления                 студентов                 вузов                 [4-5].

Достижение учащимися высоких показателей качества обучения возможно через мотивированную учебную деятельность при условии активности обучаемых в процессе решения поставленных перед ними дидактических и методических задач. Поставив перед собой цель, обучаемый, выступая в качестве субъекта деятельности, должен определить ее компонентный состав, а также четко сформулировать и впоследствии успешно реализовывать определенную последовательность необходимых учебных действий. Повышение мотивации к обучению неразрывно связано с формированием и последующим развитием у студентов теоретического и практического мышления, при этом теоретическое мышление направлено на получение учащимися общих теоретических основ по необходимым учебным дисциплинам, тогда как практическое мышление ориентировано на решение студентами конкретных практических, в том числе прикладных и профессиональноориентированных задач.

При отсутствии применения информационно-коммуникационных технологий во время проведения аудиторных занятий у студентов проявляется слабая мотивационная составляющая к учебной деятельности и формируется низкий уровень практического мышления в силу ограничения времени проведения данных занятий, что, в свою очередь, отрицательно сказывается на качестве получения студентами знаний, умений и навыков, необходимых при реализации решения задач в дальнейшей профессиональной деятельности.

Использование расчетных проектов при обучении математике

Для повышения уровня практического мышления студентам предлагается решение практических задач в рамках домашней или контрольной домашней работы, а также реализация учащимися необходимых в соответствии с учебным планом курсовых работ или проектов.

Выполнение студентами расчетных проектов по математике подразумевает реализацию на основании полученных значений исходных данных необходимых расчетных процедур с применением арифметических и логических операций для получения и визуализации значений определенных промежуточных и итоговых результатов проекта, включающего решение взаимосвязанных задач.

Несомненным достоинством данного метода является рассмотрение решения не набора отдельно взятых независимых расчетных задач, а реализация полноценного проекта с формулировкой общей цели, в рамках достижения которой предлагается решение определенного круга крупных задач с последующим их разделением на отдельные малые расчетные задачи. Следует отметить необходимость визуализации всех промежуточных этапов решения задач проекта с точки зрения оценки процесса решения и проверки значений параметров, полученных аналитических путем. Однако при реализации учебного процесса с использованием расчетных проектов возникают недостатки, заключающиеся в трудоемкости проверки преподавателем правильности выполнения студентами большого количества арифметических и логических операций при реализации расчетного проекта в силу различных комбинаций значений исходных данных и выполняемых студентами расчетных процедур и, как следствие, трудоемкости составления преподавателем большого количества различных вариантов исходных данных для проектов, высокая степень получения ошибочной информации при выполнении студентами и проверки преподавателем расчетных проектов.

Реализацию трудоемких расчетных проектов студентами вузов целесообразно осуществлять на дистанционном уровне в силу необходимости предоставления большого количества времени на реализацию студентами соответствующих арифметических и логических операций, возможностями быстрого получения информации о корректности указываемых значений промежуточных и итоговых результатов вычислений, а также необходимости предоставления в любой момент времени быстрого доступа студента к выполняемому учебному проекту в удаленном режиме с использованием сети Интернет.

Несмотря на видимые достоинства имеющихся систем дистанционного обучения («Прометей», « WebTutor », «Moodle» и т.д.), которые заключаются в автоматизации процесса обработки информации о студентах, преподавателях и учебных дисциплинах, организации общения посредством форумов и электронной почты, представлении лекционного материала в виде текстовых документов или презентаций, реализации проверки знаний студентов с применением статических тестовых систем, данные информационные системы обладают определенными существенными недостатками. В частности, в системах дистанционного обучения отсутствуют динамические средства для реализации полноценных расчетных проектов, в рамках которых по указанным комбинациям числовых значений исходных данных осуществлялись бы расчеты необходимых значений промежуточных и итоговых результатов.

Основные особенности дистанционной системы динамических расчетных проектов

Разработанная автором и используемая в процессе обучения математике студентов вузов дистанционная система динамических расчетных проектов располагается в рамках динамического Интернет-сайта разработчика программы по адресу и построена на реализации принципов автоматической генерации информационной системой различных вариантов значений исходных данных, выполнении студентами расчетных процедур, необходимых для получения определенной последовательности значений промежуточных и итоговых результатов и включающих различные взаимосвязанные арифметические и логические операции, а также проведения дистанционной системой в автоматизированном режиме сравнительного анализа рассчитанных и указанных студентами значений определенных расчетных параметров с рассчитанными в соответствии с программными алгоритмами информационной системой значениями данных компонентов [6-14].

В рамках информационной системы используется единая реляционная база данных по расчетным проектам и работам в рамках проектов, при этом учитывается взаимосвязь между участниками учебного процесса и расчетными проектами с целью реализации единого учебно-методического комплекса по изучаемым студентами дисциплинам в однородных вузах.

Основным достоинством информационной системы является реализация полноценных динамических расчетных проектов с точки зрения необходимых дидактических и методических составляющих проектной деятельности учащихся, включающих описание курса в рамках учебной дисциплины, список наименований и описание расчетных проектов в рамках курса, список наименований расчетных работ в рамках проекта, описание, демо-версии, список коэффициентов исходных данных и результатов, а также расчетные задания по работам в рамках каждого расчетного проекта. С точки зрения каждой расчетной работы применяется автоматизированная генерация независимых вариантов демо-версий (значений исходных данных, промежуточных и итоговых результатов) для преподавателя и студента с возможностями просмотра демо-версий противоположными представителями учебного процесса и администрирования только одной из сторон. Генерация заданий (вариантов значений исходных данных) для расчетных работ студентов производится однократно, преподаватель может получить доступ к работе студента только в режиме просмотра, студент может получить доступ к своей расчетной работе с возможностью просмотра правильно указанных значений, просмотра и редактирования ранее указанных неправильных значений промежуточных и итоговых результатов. Следует отметить, что реализация демо-версий расчетной работы преподавателя и студента, а индивидуального задания для студента осуществляется согласно разрабатываемому на программном уровне алгоритму решения соответствующих задач в рамках расчетной работы.

На рис. 1 представлены основные методические составляющие учебной деятельности для студентов и преподавателя при работе в рамках рассматриваемой информационной системы с точки зрения организации работы в рамках учебного курса, расчетного проекта в рамках учебного курса, а также расчетной работы в рамках расчетного проекта.

Организация процесса обучения математике с применением дистанционной системы динамических расчетных проектов осуществляется согласно следующему алгоритму.

На первом этапе преподавателем формулируются необходимые методические и дидактические составляющие учебного процесса с использованием проектной деятельности. Требования включают: описание курса в рамках учебной дисциплины, список наименований и описание расчетных проектов в рамках каждого курса, список наименований, описание и теоретический аспект по работам в рамках расчетных проектов с последующим отражением необходимых составляющих в рамках информационной системы.

Во-вторых, непосредственно преподавателем или администратором совместно с преподавателем осуществляется разработка необходимых расчетных алгоритмов и соответствующих программных модулей для реализации определенных арифметических и логических операций, применяемых при решении задач в рамках расчетных работ проекта с точки зрения определенной учебной дисциплины с последующим отражением указанных составляющих в рамках информационной системы.

На третьем этапе преподавателем и студентами осуществляется генерирование независимых вариантов демо-версий рассматриваемой расчетной работы для преподавателя и студента с возможностями просмотра демо-версий обоими представителями и администрирования только одной из сторон. Получение автоматически рассчитанных значений промежуточных и итоговых результатов осуществляется на основе генерирования значений исходных данных с использованием случайных чисел в соответствии с указанным числовым диапазоном и сформированного исходного кода программного модуля реализации расчетной работы.

После этого студентами осуществляется активация соответствующего варианта расчетной работы в рамках проекта, то есть генерирование значений исходных данных с использованием случайных чисел и определенных условий в соответствии с исходным кодом программного модуля решения задач работы. Преподавателем может осуществляться просмотр (без возможности редактирования) указанных студентом значений промежуточных и итоговых результатов выполняемой студентом расчетной работы, тогда как для студента предоставляются возможности просмотра правильно введенных значений, просмотра и редактирования указанных ранее неправильных значений промежуточных и итоговых результатов расчетной работы.

Деятельность студента

Ознакомление с описанием учебного курса

Ознакомление с описанием расчетного проекта

Ознакомление с описанием расчетной работы

Анализ демо-версий расчетной работы преподавателя

Генерирование и анализ собственных демо-версий расчетной работы

Получение значений исходных данных по расчетной работе

Решение расчетной работы вручную или с помощью компьютерных математических систем

Ручной ввод собственных значений результатов по расчетной работе

Анализ корректности указанных собственных значений результатов по расчетной работе

Виртуальное общение с преподавателем в рамках расчетной работы

Переход к выполнению следующей в проекте расчетной работы

Переход к следующему расчетному проекту в учебном курсе

Информационная система

Поиск и вывод описания учебного курса

Поиск и вывод описания расчетного проекта

Поиск и вывод описания расчетной работы

Генерирование и вывод собственных демо-версий расчетной работы для преподавателя

Генерирование и вывод собственных демо-версий расчетной работы для студента

Генерирование собственных значений исходных данных и результатов расчетной работы для студента

Генерирование формы для ввода собственных значений результатов по расчетной работе для студента

Сравнительный анализ указанных студентом собственных значений результатов с автоматически рассчитанными значениями

Реализация форума для виртуального общения преподавателя и студента в рамках расчетной работы

Автоматизация перехода к выполнению следующей в проекте расчетной работы

Автоматизация перехода к следующему расчетному проекту в учебном курсе

Деятельность преподавателя

Рассмотрение описания учебного курса со студентами

Рассмотрение описания расчетного проекта со студентами

Рассмотрение описания расчетной работы со студентами

Генерирование и анализ со студентами собственных демо-версий расчетной работы

Анализ индивидуальных демо-версий расчетной работы студента и обсуждение работы со студентом

Мониторинг процесса выполнения индивидуальных расчетных работ студентами (анализ корректности указываемых студентом собственных значений результатов на основе индивидуальных значений исходных данных)

Виртуальное общение со студентами в рамках расчетной работы

Переход к следующей в проекте расчетной работы

Переход к следующему расчетному проекту в учебном курсе

Рис. 1. Организация учебной деятельности в информационной системе

Затем осуществляется реализация мониторинга проектной деятельности студентов с точки зрения как преподавателя, так и студента, с целью проведения анализа процесса выполнения студентом расчетной работы и формированием дальнейшей стратегии реализации текущей проектной деятельности.

Ключевым функциональным моментом информационной системы является выполнение студентом динамических расчетных проектов и работ. Генерация значений исходных данных и загрузка макета работы осуществляется автоматически по требованию студента, при этом в рамках макета работы значения коэффициентов исходных данных окрашиваются в зеленый цвет, а вместо значений результирующих коэффициентов указываются визуальные текстовые поля, залитые серым цветом, для непосредственного ввода значений, которые окрашиваются в красный цвет. Проверка корректности указанных студентом значений промежуточных и итоговых результатов осуществляется при нажатии на соответствующую кнопку. После активации проверки введенных в текстовые поля значений результирующих коэффициентов корректные значения коэффициентов промежуточных и итоговых результатов визуально заменяются текстовыми надписями, окрашиваемыми в синий цвет, а указываемые студентом неправильные значения коэффициентов промежуточных и итоговых результатов визуально не изменяются и отображаются в виде текстовых полей для ввода значений, но с отображением последнего указанного студентом неправильного значения коэффициента, окрашиваемого в красный цвет (рис. 2).

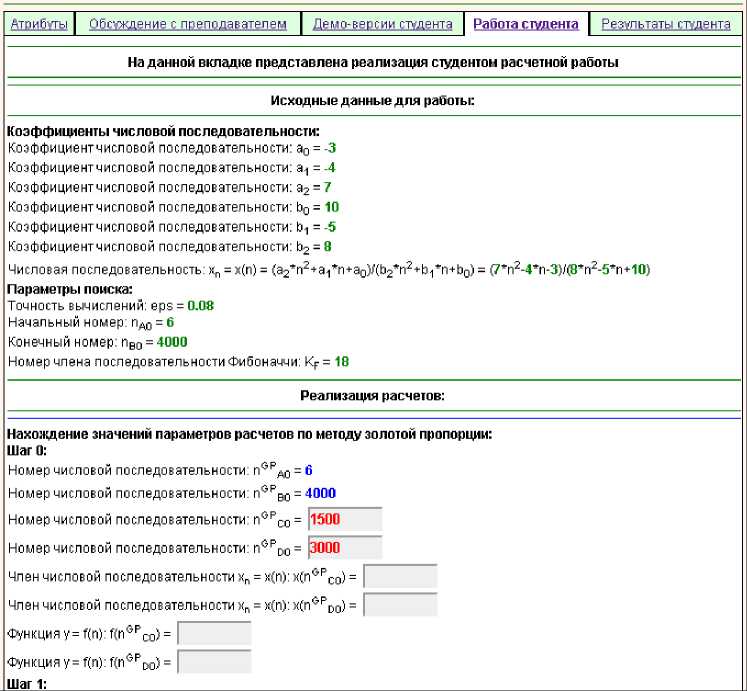
Рис. 2. Результаты выполнения студентом динамического расчетного проекта

В дистанционной системе присутствует возможность многократного изменения студентом значений коэффициентов промежуточных и итоговых результатов и автоматизированной проверки указанных значений данных параметров информационной системой в рамках расчетной работы, то есть выполняемая студентом расчетная работа предоставляется в режиме редактирования без учета временных и пространственных ограничений.

Динамические расчетные проекты по математике

Рассмотрим реализуемые студентами вузов расчетные проекты по исследованиям функций вещественного переменного, которые используются при изучении дисциплины «математика». В рамках дистанционной системы динамических расчетных проектов представлены четыре расчетных проекта по данному разделу математики, которые базируются на примени численных методов решения поставленных задач [15-18].

В рамках первого расчетного проекта «Определение значений минимальных номеров приближения к пределу числовых последовательностей» необходимо

реализовать расчет значений промежуточных и итоговых результатов вычислений необходимых расчетных параметров при нахождении значений минимальных

номеров

a₂n + a 1 n + a₀

n2

b₂n + b 1 n + b₀

приближения к пределу числовых последовательностей вида

(для £ >  0 ,    a 2 ^ ⁰, ^b 2 ^ ⁰,

x n —

a

² <  £)

b 2      ⁾

с

использованием методов золотой пропорции, Фибоначчи, половинного деления (дихотомии) в зависимости от заданных значений исходных данных.

Во втором расчетном проекте «Приближенные решения алгебраических уравнений» осуществляется расчет значений промежуточных и итоговых результатов вычислений необходимых расчетных параметров при реализации приближенных решений алгебраических уравнений вида ax³ + bx² + cx + d = 0 с использованием метода половинного деления (дихотомии), комбинированного метода хорд и касательных (Ньютона), метода золотой пропорции в зависимости от заданных значений исходных данных.

В рамках третьего расчетного проекта «Приближенные вычисления значений определенных интегралов» реализуются расчеты значений промежуточных и итоговых результатов вычислений необходимых расчетных параметров при нахождении приближенных значений определенных интегралов для функции вида f (x ) =

a₁x + a₀ b 1 x + b₀

по формулам средних прямоугольников, прямоугольных трапеций,

параболических трапеций (Симпсона) в зависимости от заданных значений исходных данных.

В четвертом расчетном проекте « Приближенные решения обыкновенных

дифференциальных уравнений первого порядка» осуществляется расчет значений

промежуточных и итоговых результатов вычислений необходимых расчетных

параметров при реализации приближенных решений дифференциальных уравнений

первого порядка вида

У' = f ^{( Х,}У ^{( x} ))

для функции

f ( х,У ( x )) = ax + by

с

использованием методов Эйлера, Рунге-Кутта второго, четвертого порядков точности в зависимости от заданных значений исходных данных.

Представим описание демо-версии дистанционного динамического расчетного проекта «Определение значений минимальных номеров приближения к пределу числовых последовательностей» на примере реализации дистанционной системой динамических расчетных проектов расчетов значений промежуточных и итоговых результатов вычислений при нахождении минимальных номеров ne для заданной

_ a2n2 + a1n + a0 _ - 5n2 - 4n - 4 числовой последовательности xn = ” 2 i \ =              7 и b2n + b1n + b0   - 7n + 4n - 5

параметров поиска  e = 0,05 , пао = 6 , пво = 5000 и KF = 16 в сопровождении соответствующих скриншотов программы для ЭВМ.

По автоматически сгенерированным дистанционной системой динамических расчетных проектов значениям исходных данных осуществляется вывод в виде автоматически создаваемой статической Интернет-страницы полученных значений исходных данных (рис. 3), а также информации о рассчитанных значениях промежуточных и итоговых результатов вычислений по методам золотой пропорции (рис. 4), Фибоначчи (рис. 5) и половинного деления (дихотомии) (рис. 6).

Рис. 3. Формирование значений исходных данных

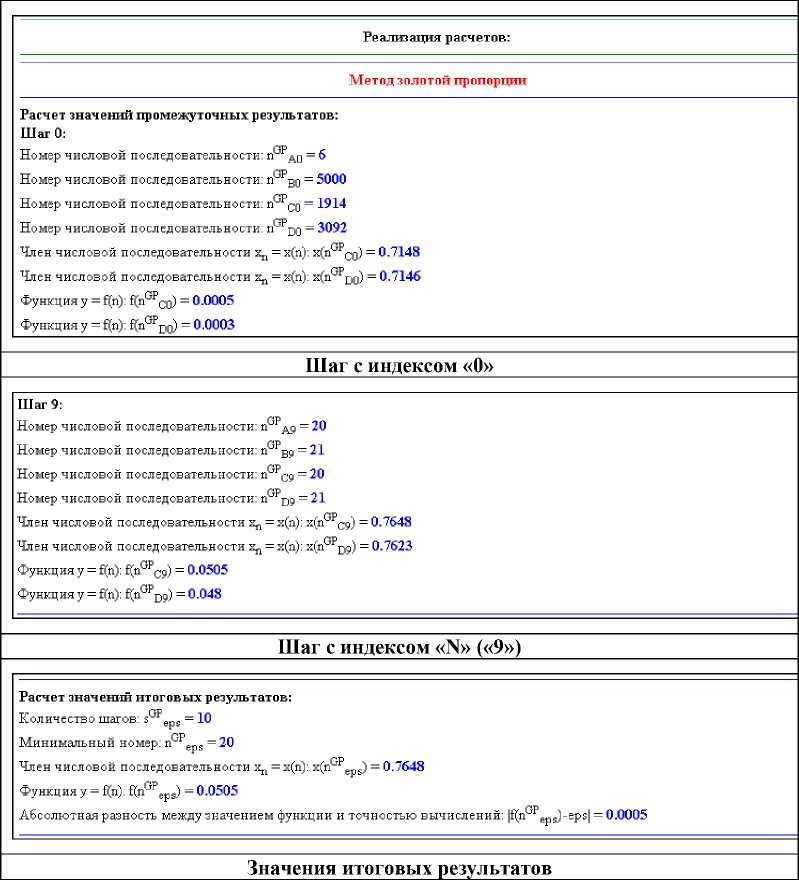
Рис. 4. Расчет значений параметров промежуточных и итоговых результатов по методу золотой пропорции

Рис. 5. Расчет значений параметров промежуточных и итоговых результатов по методу Фибоначчи

	Метод половинного деления (дихотомии)

Расчет значений промежуточных результатов:

Шаг 0:

Номер числовой последовательности: п^Сдд = 6

Номер числовой последовательности: n^DgQ = 5000

Номер числовой последовательности: h^qq = 2503

Член числовой последовательности ^ = x(n): х(п%о) = 0.7147

Функция у = f(n): f(n^DcQ) = 0.0004

Шаг с индексом «0»

Шаг 12:

Номер числовой последовательности: п^д^” 20

Номер числовой последовательности: n^Dgi2 ⁼ 21

Номер числовой последовательности: n^DQi2 ⁼ 21

Член числовой последовательности ^ = x(n): x(n^Dd2) ~ 0.7623

Функция у = f(n): f(n^DQi2) 0-048

Шаг с индексом «N» («12»)

Расч е т знач е ний и т о г ов ых р езуль т ат ов:

Количество шагов s^D_eps: s^D_eps = 13

Минимальный номер n^_eps: n^_eps =20

Член числовой последовательности x_n = x(n): x(n^D_epg) = 0.7648

Функция у = f(n): f(nDepg) = 0.0505

Абсолютная разность между значением функции и точностью вычислений: |f(n^D_epg)-eps| = 0.0005

Значения итоговых результатов

Рис. 6. Расчет значений параметров промежуточных и итоговых результатов по методу половинного деления (дихотомии)

Анализ и оценка разработки

Внедрение рассматриваемой информационной системы в образовательный процесс осуществляется параллельно с изучением соответствующих разделов математики на аудиторных занятиях и согласно проведенным тестовым методикам до и после внедрения системы в обучение показало существенный рост у студентов мотивации к обучению и развитие практического мышления. С точки зрения проведения аудиторных занятий в рамках изучения соответствующей темы на лекциях целесообразно рассмотрение преподавателя со студентами теоретического материала в рамках описания учебного курса, расчетных проектов и работ, тогда как на практических занятиях преподавателем совместно со студентами необходимо осуществлять генерирование, активацию, изучение и проведение сравнительного анализа демо-версий расчетных работ как для преподавателя, так и для студента, с необходимыми комментариями. Также на практических занятиях целесообразно проводить сравнительный анализ результативности выполнения студентами динамических расчетных работ с необходимыми консультациями.

Заключение

Таким образом, дистанционная форма организации самостоятельной деятельности студентов вузов в процессе обучения является наиболее оптимальной, однако при отсутствии расчетной проектной деятельности учащихся дистанционное обучение сводится только к изучению электронных учебников и выполнению необходимого тестирования в качестве оценки качества полученных знаний, что приводит к понижению интереса и мотивации к учебной деятельности, а также отсутствию полноценного формирования у обучаемых теоретического и практического мышлений в рамках интеграционной взаимосвязи получаемых во время обучения в вузе знаний, умений и навыков, необходимых для эффективной реализации студентами будущей профессиональной деятельности. Используемая при реализации самостоятельной деятельности учащихся по математике разработанная автором дистанционная система динамических расчетных проектов не только позволяет комбинировать дистанционную форму обучения с выполнением студентами полноценных расчетных проектов, но и способствует повышению у обучаемых мотивации к изучению математике и развитию практического мышления.