Развязка противоречий в моделях исторических явлений

Математические модели реальных, в частности, исторических явлений, как правило, чрезвычайно сложны, а соответствующие им системы ограничений – противоречивы, что приводит к необходимости использования дополнительных корректирующих процедур. В работе содержится краткий обзор подхода к коррекции таких систем, развиваемого авторами и опирающегося на теорию дискретных обобщенных решений несовместных систем ограничений и коллективных методов обучения распознаванию образов. Исследование выполнено в рамках междисциплинарной программы УрО РАН «Историческая динамика России: факторы, модели, прогнозы».

OUTCOME OF CONTRADICTIONS IN THE MODELS OF HISTORICAL PHENOMENA

Vl.D. Masurov, M.Yu. Khachay

Mathematic models of real, particularly historical phenomena, are as a rule extremely complicated, and systems of limitation corresponding to them are contradictory that entails the necessity of correcting procedures. A brief review of approaches to correction of such systems developed by the authors and basing on the theory of discrete generalized solution of inconsistent limitation systems and collective methods of teaching to image detecting is offered in the article. The research is implemented under the interdisciplinary program of the Urals Department of RAS 'Historical dynamics of Russia: factors, models, forecast'.

При построении математических моделей пытаются удовлетворить естественному требованию их непротиворечивости. Однако на самом деле это требование не всегда отвечает существу ситуаций моделирования. Например, при описании некоторых задач экономического планирования (особенно в случае предреволюционных ситуаций) часто выясняется, что эти задачи приводят к несовместным системам ограничений, отражающих действительно противоречивые требования экономической системы. Противоречивые задачи естественным образом возникают и при проектировании технических объектов. Критерии выживания биологических систем также могут быть несогласованными друг с другом.

Инконсистентные логики – одно из направлений современной логики. Таким образом, во многих случаях появляются противоречивые математические модели, которые необходимо конструктивно использовать в соответствии с содержательным смыслом рассматриваемой задачи. Наш аппарат – анализ предложений инконсистен-тной логики на основе тупиковых подсистем противоречивой системы соотношений.

Поскольку, однако, не имеет смысла рассматривать любые противоречивые математические модели, необходимо выделить те из них, которые отвечают некоторым условиям обобщенной непротиворечивости. В связи с этим могут быть введены различные обобщения понятий непротиворечиво- сти и существования. Например, систему неравенств можно назвать s-непротиворечивой, если любые ее s неравенств составляют совместную подсистему. Обобщение понятий существования и непротиворечивости теоретических моделей могут быть получены и на основе применения комитет-ных конструкций [1].

Мысль о том, что противоречивые знаковые модели можно использовать конструктивно, не нова (достаточно упомянуть о методе наименьших квадратов, о чебышевских приближениях), но в последнее время с этой идеей связан более широкий подход, в рамках которого рассматриваются не только несобственные задачи оптимизации и классификации [2], но и противоречивые системы в логике (рассматривается, например, локальная непротиворечивость аксиоматических систем [3, 4]). Можно рассматривать максимальные непротиворечивые подсистемы заданной системы аксиом или системы аксиом, не приводящие к противоречиям при длине вывода, не превышающей заданную.

В данной статье приводятся некоторые примеры конструктивного использования противоречивых математических моделей.

Неоднозначность разбиения

Разбиение системы на подсистемы, выделение объектов, предметов – операция неоднозначная, и при ее формализации можно получить противоречивую математическую модель, с которой необходимо работать как с несобственной задачей классификации (таксономии). Действительно, пусть задано множество ^c^’ для которого надо получить разбиение на таксоны. Предположим, что задана совокупность /" допустимых множеств, задающая возможные таксоны:

^^JeJ^, т.е. если ^ = U4 - разбиение множества A на таксоны, то для любого i должен найтись номерJeJ такой, что '^^

Запишем систему относительно неизвестного номера j E 3

aev^Vae j4)Je J.         G D

Смысл этой системы такой: мы пытаемся все множество 4 представить как один таксон, подобрав соответствующее вмещающее его множествоV,G . Понятно, что в общем случае эта попытка невыполнима и, следовательно, система (1), несовместна. Поэтому в данной ситуации естественно применить понятие максимальной совместной подсистемы системы (1), которой соответствует максимальное по включению BcAудовлетворяющее условию: система a ev^a e B^Je J совместна. МножествоВ называется индексом этой подсистемы.

Пусть q - число всех максимальных совместных подсистем системы (1.1) и мно-жестваA,..., 4- индексы этих подсистем. С целью нахождения разбиения на таксоны запишем соотношения:

л = ид,4П4=^*JY

.

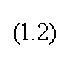
Система (1.2) тоже может быть несовместной, так как в общем случае индексы максимальных совместных подсистем могут пересекаться.

Поэтому можно отыскивать наборы

B₁cA(>fi).A=UB₁,B_;r\B, = 0 (,i*j). (1.5.

Решение последней задачи неоднозначно, которую можно преодолеть, введя критерий, например, такой:

пвх^р:(|4П5|5:р|4| либо ^nSH^XW6!,?} 5A.

Противоречивые системы геометрических предикатов

Пусть Х^^.рДО - предикат, значение которого равно 1 или 0 в зависимости от того, обладает или нет множество Х соответствующим свойством i= ],...,№

Запишем систему

Мазуров Вл.Д., Хачай М.Ю.

(1.5) .

Система (1.5) может быть противоречивой, и тогда она будет определять совокупность множеств в , каждое из которых соответствует некоторой максимальной совместной подсистеме системы (1.5). Таким образом, системе (1.5) соответствует некоторая модель реального объекта с его неоднозначной интерпретацией.

На основе метода выделения максимальных совместных подсистем можно объяснять явления неоднозначности интерпретаций некоторых изображений (куба Неккера [5] и других).

Комитеты в математическом программировании

В практике часто возникают ситуации, моделируемые противоречивыми задачами математического программирования. Содержание некоторых из них согласуется со следующей конструкцией.

Пусть система ограничений

//х) < OQ-1,. „Мхе R”

несовместна, К - множество всех ее p-комитетов, члены которых принадлежат заранее фиксированному ограниченному множеству D. Тогда в задачу sup[/(x) : ^(х) < 0(j = 1, ...,«)j вкладывается смысл:

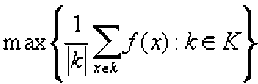
Здесь p-комитет понимается как смешанная стратегия использования его членов с одинаковыми вероятностями, и максимизируется математическое ожидание значения функции цели при использовании таких смешанных стратегий.

Одна игровая задача, связанная с принятием решений большинством голосов

Пусть X - произвольное непустое множество и

Рассмотрим не обязательно совместную систему включений

(2.1)

Будем говорить, что x0 - решение (2.1), если         Как обычно (см., например,

[6]) конечную последовательность

6 = (x1,x2,.„x,j назовем комитетом большинства из q элементов (или просто комитетом) системы (2.1), если для каждого j е Nm выполнено условие

.                                              (2.2)

Ниже дается ответ на вопрос: "Пусть система (2.1) обладает комитетом из q элемен- тов; насколько мала по отношению к мощности всей системы может быть мощность ее наибольшей подсистемы, разрешимой комитетом из k элементов?". В целом изложение данного раздела следует работам [7,8].

Обозначения

Пусть              - комитет системы

• (2.1).    Сопоставим ему { 1, - 1 } -матрицу A размера по правилу:

• 1,    если х' eD , ви/юти-зм^ c^j^

Через ajобозначим j-ю строку матрицы.

По условию,           при каждом jeN„

Каждому подмножеству сопоставим:

• -    вектор                где - i-й орт

пространства

• -    множество                   и

• -    число           равное относитель

ной величине мощности подсистемы J(I) системы (2.1), разрешимой комитетом из k элементов с номерами из множества I

Матрице A сопоставим число

<5₉ ,(Л) = max{^(/,A): I с N„| J|= fc)

Обозначим через M(q) множество всех -матриц с q столбцами, обладающих свойством        для каждого j. Рассмотрим антагонистическую игру        с приро дой, в которой множество стратегий 1-го игрока                  , множество стратегий 2-го игрока (природы) Y = M(g)

а функция выигрыша km^w

Для ответа на основной вопрос работы най-

и \™б₂₁-_№1-Уг (2.7)

дем верхнюю цену игры б . = min б (-4) = min max б .(Л, Г)

(2.3)

Результаты

СЛЕДСТВИЕ 1. Для произвольного на турального k lim 5^ = ^ + 0

Положим s

^ + 12

и t

СЛЕДСТВИЕ 2. Пределы (2.5) и (2.6) как функции аргумента p удовлетворяют соотношениям:

ТЕОРЕМА 1. Для произвольных натуральных ^ \ l7 справедливы равенства

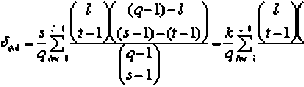
(«НН ) (Л-l) (_t-i)J (2.4)

Неожиданным следствием теоремы яв-

и

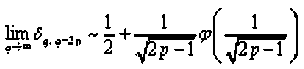
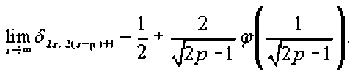
ЗАКЛЮЧЕНИЕ

ляется следующее равенство:

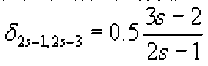
Видно, что ^j-L2)-3 монотонно возрастает с ростом s и lim4,.U1_, = %

ЗАМЕЧАНИЕ. Для произвольных k

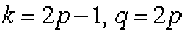
при произвольном натуральном p, игра неразрешима в чистых стратегиях, поскольку

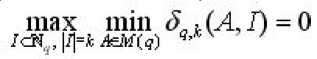
ТЕОРЕМА 2. Игра Г разрешима в смешанных стратегиях, при этом цена игры совпадает с '""^Л и определяется по формуле (2.4).

Заметим, что оптимальная стратегия природы не зависит от k и определяется неоднозначно.

Найдем приближенные формулы для вычисления ^4 ^ при больших q и добавочном условии на выбор k:k=q-n, где n -фиксированное натуральное число.

ТЕОРЕМА 3.

• 1.    Пусть n=2p, где pe N, справедливо равенство

• 2.    Если n=2p-1, то hm<5' не существует, поскольку

S‘5«-^ = >2(1+^-^-1’^) (2.5)

В теореме 1, фактически, доказано новое необходимое условие существования комитета системы (2.1).

Поскольку точные формулы оценок имеют вид сумм вероятностей гипергеометрических законов, то теорема 2 может рассматриваться вне контекста теории комитетных решений в качестве аналога предельной теоремы.

Особый интерес вызывают следствия. Исходя из здравого смысла следовало бы, например, ожидать, что ^-2-^1

Однако это не так. Этот факт удобно интерпретировать в терминах "голосования" и "кворума". В самом деле, пусть некоторая комиссия из q депутатов принимает или отклоняет законопроекты методом голосования простым большинством голосов. Допустим, известно, что на очередной рабочий день было запланировано рассмотреть m законопроектов. Известно, что, если на заседание явилась бы вся комиссия целиком, то все законопроекты были бы приняты. Из доказанного выше следует, что если хотя бы двое депутатов будут отсутствовать, то в худшем случае комиссия примет не более законопроектов при условии, что все оставшиеся ее члены не изменят своего решения и будут голосовать так, как они голосовали бы при полном ее составе.

Мазуров Вл.Д., Хачай М.Ю.