Reactivity as one of the criteria for the selection of raw materials for the production of active fine mineral powders

Original article

C urrently, the search and study of alternative raw materials suitable for the production of fine mineral powders is an important scientific and practical task, the solution of which will allow a more widespread introduction of resource-saving technologies in the production of composites for construction purposes. Currently, the scope of mineral powders application in the building materials industry is very extensive: mineral powders are used as pozzolans additives [1–3]; fillers for concrete and soil-concrete mixtures [4, 5]; raw mixtures for obtaining products by dry or wet pressing [6, 7].

The simplest and most common method of obtaining fine mineral powder is mechanical dispersion. During mechanical grinding of a solid, a surface identical in nature to the original one is formed [8].

It is known that in the process of mechanical dispersion, a certain amount of work (energy) is spent, which is then spent on elastic and plastic deformation, the heat released and on the formation of a new surface. At the same time, in solids, processes are possible, in which the formation of a new surface can also affects the bulk phase. Therefore, there is always the question of whether the destruction of the crystal lattice of a solid actually leads to the activation of the resulting crushed material.

Thus, it was shown in [9–11] that the key characteristics of finely dispersed mineral powders, by which activation processes can be judged, are the specific surface area (Ssp), which characterizes the degree of dispersion of the material and the specific free surface energy, numerically equal to the surface tension (σ) of the solid. Therefore, to evaluate the process of mechanical activation of raw materials, a number of models based on the determination of these characteristics were proposed.

Thus, the authors [12] have developed a mathematical model based on the determination of the magnitude and sign of the change in the isobaric-isothermal potential of the surface ∆GS (Gibbs energy), accompanying the process of grinding mineral raw materials. This parameter, according to the authors, is a criterion for the possibility of spontaneous transformation processes occurring during mechanical dispersion of materials [13–14].

Continuing research in this direction, the authors of [15, 16] believe that for fine powders, the most important characteristic is the energy state of the system, estimated by the value of free surface energy (ES). Based on the classical concepts of colloidal chemistry, this value can be calculated as the product of the surface tension and the specific surface of the analyzed object [17, 18].

Further development of this direction allowed us to propose, in our opinion, a new, more advanced model for assessing the degree of activation of the material during its dispersion. This approach is based on the determination of the relative change in the free surface energy of the material when obtaining a dispersed system [19–21]. The mathematical description of this approach is the expression (1) combining experimentally determined values of the surface tension of the system and its specific surface:

ДР / ^ \

— = (1-6(7)- -1, (1) ^-sO X^spO/ where “0” – index denoting the initial state of the system; δ – relative change in the value of the surface tension, determined by the formula:

Act CT; - CTn

, (2)

°b °b

σ0 – initial surface tension of the system; σi – surface tension of the system, after the dispersion process; ∆ES/ES0 – relative change in the free surface energy.

At the same time, in the works [22–24], the selection of the most effective raw materials for the production of composite binders is carried out on the basis of the surface activity criterion (ks), which shows the share of the total potential energy reserve of the analyzed rock obtained as a result of its genesis, transferred to the surface in the process of mechanical activation of raw materials. The calculation of the parameter ks is carried out based on the chemical composition of the material, the specific surface area of the system and the free surface energy of the unit surface area (σ).

The surface activity parameter is based on macro-energy indicators of the analyzed raw materials - atomization energy (EA, kJ/mol) and its specific values – volumetric specific atomization energy (energy density – EV, kJ/

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS cm3) or mass specific atomization energy (Em, kJ/g) [15]. Therefore, the value of ks can be used as a criterion characterizing the reactivity of fine mineral powders after their mechanical disintegration. In [20], the value of ks was determined for a number of sedimentary rocks.

Based on the above, the purpose of this work was to calculate the relative change in the surface energy of fine mineral powders of various raw materials by expression (1); to identify a possible functional relationship between the parameter ∆E_S/E_S0 and the amount of surface activity for the studied rock systems.

METHODS AND MATERIALS

Two rocks of the Arkhangelsk region were selected as materials for research [23]. This is the quarry sand of the “Kenitsa” deposit. As another object of research, saponitecontaining a material (a representative of bentonite clays) isolated by electrolytic deposition from a suspension of recycled water from the enrichment process of kimberlitic ores of the M.V. Lomonosov diamond deposit was used [21].

Before starting the experiments, the sand was washed and dried to a constant weight at 105оC. Sands size modulus and their true density (by picnometric method) were determined according to GOST 8735-88. The true density for clay (saponitecontaining material – SCM) was determined according to GOST 21216-2014. The chemical composition of the samples was determined on an X-ray fluorescence analyzer “MetExpert”.

Highly dispersed rock fractions were obtained by dry grinding on the Retsch PM100 planetary ball mill. Optimal operating parameters of dispersion were selected experimental for each test sample. They make it possible to obtain high reproducibility of the results in terms of particle size characteristics (at least three parallel tests). The rotation speed of the mill rotor was 420 rpm. For dispersion, tungsten carbide grinding bodies of spherical shape in the amount of 20 pieces and a grinding cup made of the same material were used.

The dimensional characteristics were determined using a submicron particle size analyzer Delsa Nano Series Zeta Potential and Submicron Particle Size Analyzers (“DelsaNano”) by photon correlation spectroscopy based on the principle of dynamic light scattering. The specific surface of highly dispersed rock systems was determined by the gas permeability method on the PSX-10 device.

To calculate the surface tension, the wetting edge angle was measured at the “Easy Drop” installation at an ambient temperature of 25±1оC. The study was performed on tablet samples made by pressing ground sand and saponite-containing material on a PLG-20 press (20 kPa load) into a metal mold with a diameter of 20 mm. The surface tension for highly dispersed samples was calculated by the Owens–Wendt–Rabel–Kaelble (OWRK) method, based on the measurement of the equilibrium wetting angle (θ) by liquids (distilled water, decane, glycerin and ethylene glycol) with known values of surface tension and its dispersion (σLD) and polarization (σLP) components.

At the same time, the obtained functional dependencies of the QWRK method:

^aL " (cos0 + 1) _ /л/с^А (3) 2-V^f YVO?)

are described by linear equations, where θ – wetting angle of the material under study, σL, σLD and σLP – the total, dispersion and polarization surface tensions of working fluids (respectively). The angular coefficient of this linear dependence is equal to the polarization part of the surface tension of the sample, and extrapolation of this straight line to the ordinate axis allows us to calculate the dispersion component. The surface tension of the analyzed samples is calculated by the following expression: σS = σSP + σSD, where σSP and σSD this polar and dispersion components of the surface tension of the material under study, J/m2.

The calculation of the relative change in surface energy was carried out according to the expression (1). The value of the surface energy was calculated as the product of the specific surface of the analyzed powder by its surface tension.

RESULTS AND DISCUSSION

The results of determining the granularity of the studied sand sample of the “Kenitsy” deposit showed that it can be classified as medium-sized sand (modulus of size 2.21). The obtained values of the true densities (ρreal) of the studied rocks showed similar results: 2640 kg/m3 and 2630 kg/m3 for polymineral sand and saponitecontaining material (SCM), respectively.

The initial data for calculating the atomization energy of rocks are the mineral composition of the studied samples in terms of oxides, as well as the enthalpy of formation of the corresponding oxides, the values of which are given in the reference literature [25]. Taking into account the molecular weight of the oxide compounds, the specific mass energy of atomization of the prototypes was calculated.

The elemental composition (in terms of oxides), as well as the standard enthalpy of formation of these oxides and their molecular weights are presented in Table 1.

Using the data presented in Table 1, the ЕА and Em values of the studied samples were calculated. Thus, the atomization energy for polymineral sand was 1910.72 kJ/mol, and for saponitecontaining material – 1826.94 kJ/mol. At the same time, the mass specific atomization energy for sand and SCM are 30.41•103 kJ/kg and 26.94•103 kJ/kg, respectively.

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

Table 1

The composition of the studied samples in terms of oxides, the enthalpy of formation of oxides (∆Н) and their molecular weight (M).

Oxide	Content, %		∆H 298 • 10–3, kJ/kmol	Molecular weight of the oxide, kg/kmol
	sand	SCM
SiO2	90.56	51.83	–910.94	60.09
Al 2 O 3	5.77	10.07	–1675.70	100.18
MgO	0.48	19.7	–601.50	40.31
Fe 2 O 3	0.88	10.54	–822.00	159.70
CaO	0.25	4.79	–635.10	56.08
K 2 O	0.28	1.77	–362.00	94.20
SO3	0.07	0.46	–439.00	80.06
P 2 O 5	0.06	0.76	–1507.20	141.94
Na2O	1.65	0.08	–414.84	61.98

In the continuation of the research, several fractions of highly dispersed rock powders were obtained by mechanical dispersion, which were characterized by an average particle size and specific surface area (Table 2).

The obtained values of the average particle size showed that with the same grinding parameters, the SCM dispersion process requires more energy than for sand. So, with a grinding duration of 30 minutes, and particles have an average diameter of 329 nm, while for SCM this parameter reaches a value of 664 nm.

The comparison of the specific surface area of materials, with a dispersion time of 30 minutes, have similar values: sand 2860 m2/kg, SCM – 2821 m2/kg.

Table 3 shows experimental data for measuring wetting angles (θ) and cosines of these angles for experimental samples with reference liquids obtained for the implementation of the OWRK method.

The presented data (Table 3) made it possible to calculate the surface tension (and its components) for the studied powder systems of rocks by functional dependencies (expression 3). These dependences (expression 3) are well described by linear equations of the form y = a•x + b with a high value of the approximation reliability coefficient (R2 = 0.98). The values of the coefficient of these equations and the calculated surface tension of the analyzed rock powders are presented in Table 4.

The presented data (Table 4) show that for all the samples studied, the polarization effect prevails over the dispersion interaction. As the specific surface area increases, the numerical value of the ratio σSP/σSD increases. This fact may indicate an increase in the number of active surface centers, which is associated with the redistribution of its energy potential, since for all finely dispersed

Table 2

Characteristics of highly dispersed fractions of sand and saponincontaining material

Grinding duration (τ), min	Average particle size, d, нм		Specific surface area, Ssp, m2/kg
	sand	SCM	sand	SCM
0	–*	1350	1	17
5	672	1113	781	1861
10	559	828	992	2081
20	406	764	1667	2416
30	329	664	2860	2821
60	–	519	–	3728
90	–	445	–	5067

* the parameter was not defined

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

Table 3

Wetting edge angles for test samples with different grinding duration (τ)

Sample	τ, min	Wetting edge angles, θср ±0,1
		dean		ethylene glycol		glycerin		water
		θ	cos θ	θ	cos θ	θ	cos θ	θ	cos θ
Sand	0	8.76	0.988	13.45	0.973	16.37	0.959	15.55	0.963
	5	5.36	0.996	11.88	0.979	13.65	0.972	12.98	0.974
	10	4.10	0.997	12.80	0.975	14.12	0.970	8.30	0.990
	20	8.13	0.990	9.48	0.986	10.64	0.983	3.98	0.998
	30	14.66	0.967	7.99	0.990	9.70	0.986	4.30	0.997
SCM	0	10.09	0.985	7.16	0.992	15.34	0.964	4.09	0.997
	5	7.45	0.992	9.64	0.986	13.45	0.973	3.45	0.998
	10	6.98	0.993	9.05	0.988	12.37	0.977	2.64	0.999
	20	7.05	0.992	13.58	0.972	10.32	0.984	1.87	0.999
	30	9.89	0.985	14.00	0.970	9.77	0.985	2.09	0.999
	60	10.11	0.984	13.89	0.971	9.16	0.987	2.87	0.999
	90	9.76	0.986	13.93	0.971	9.02	0.988	2.17	0.999

Table 4

Values of surface tension of rock powders depending on the duration (τ) of grinding

Sample τ, min Coefficient of the linear equation σSP, mJ/m2 σSD, mJ/m2 σk•103, J/m2 a b Sand 0 6.82 4.38 46.52 19.16 65.68 5 6.87 4.39 47.18 19.25 66.43 10 6.93 4.36 48.05 19.01 67.06 20 6.99 4.35 48.85 18.97 67.81 30 7.03 4.32 49.35 18.66 68.00 SCM 0 6.97 4.34 48.65 18.85 67.50 5 6.98 4.35 48.70 18.93 67.62 10 6.98 4.36 48.77 18.98 67.75 20 7.00 4.34 49.01 18.81 67.82 30 7.01 4.32 49.20 18.68 67.88 60 7.01 4.32 49.20 18.69 67.89 90 7.02 4.32 49.22 18.70 67.92 mineral powders, almost the same values of total surface tension (65.68 ... 68.00)•10–3 J/m2 are observed.

In the continuation of studies for fine fractions of mineral powders, the values of free surface energy (ЕS), surface activity (ks) and the relative change in free surface energy (∆ES/ES0) were calculated (Table 5).

The energy characteristics of the powders (Table 5) showed that the surface activity and the relative change in the surface energy of the system increase with increasing duration of dispersion of mineral components.

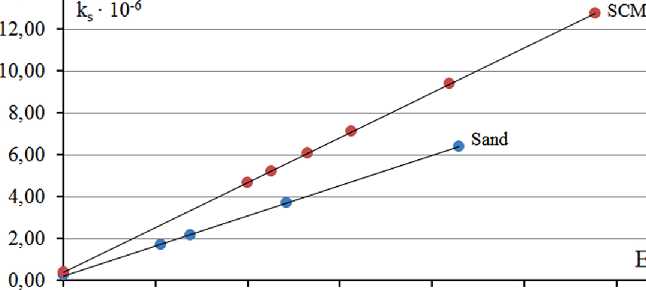
To identify a possible relationship between the values of the surface activity (ks) of rocks and the relative change in the free surface energy of the system (∆ES/ES0), functional dependencies of the form ks = f(∆ES/ES0) were constructed (Fig. 1).

The obtained functional dependences ks = f(∆ES/ES0) for the studied samples of polymineral sand and saponitecontaining material have a linear character. The mathematical expression of these dependencies are equations (4) and (5):

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS

14,00

0,00      5,00     10,00     15,00     20,00     25,00     30,00     35,00

Table 5

Energy characteristics of powders

Sample	τ, min	Free surface energy, ЕS, J/kg	Surface activity k • 106	δσ	Ssp/Ssp0	∆E s /E s0
Sand	0	8.08	0.27	–	1.00	0.00
	5	51.94	1.71	0.011	6.36	5.28
	10	66.52	2.19	0.021	8.07	6.90
	20	113.04	3.72	0.032	13.55	12.11
	30	194.50	6.40	0.035	23.25	21.43
SCM	0	11.40	0.42	–	1.00	0.00
	5	125.84	4.67	0.002	11.02	10.00
	10	140.99	5.23	0.004	12.32	11.28
	20	163.83	6.08	0.005	14.30	13.23
	30	191.49	7.11	0.006	16.70	15.61
	60	253.09	9.39	0.006	22.07	20.94
	90	344.05	12.77	0.006	30.00	28.82

Fig. The dependence of the relative change in free surface energy on the surface activity of finely dispersed mineral powders of rocks

– for sand

ДЕ57

k_s = (2,87 ■ —- + 2,27) ■ IO"⁷

"E

– for SCM

ДЕ57

k_s = (4,29 ■ —- + 4,07) ■ 10"⁷

"E

In this case, the coefficient “a”, in our opinion, characterizes the dynamics of changes in the reactivity (4)    of the material with a change in the duration of mechani cal grinding, and the parameter “b” – reactivity in the macro-state (before the start of the mechanical activation process). The data obtained from equations (4) and (5) are in good agreement with the experimental results (5) presented in Table 2.

Comparison of the coefficients “a” of the studied dispersed systems showed that, unlike polymineral sand,

MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS the reactivity of saponite-containing material increases 1.5 times faster per unit of time, as the duration of grinding increases.

Thus, it can be argued that the obtained functional relationship between the criteria used for evaluating the process of mechanical activation of mineral raw materials of various natures shows the correctness of the models used.

CONCLUSION

The calculated macro-energy characteristics of rock samples using the results of X-ray fluorescence analysis have showed that the atomization energy for polymin-

eral sand was 1910.72 kJ/mol, and for saponitecontaining material was 1826.94 kJ/mol. At the same time, the mass specific atomization energy for sand and SCM was 30.41•103 kJ/kg and 26.94•103 kJ/kg, respectively.

As mathematical models for evaluating the efficiency of the process of mechanical activation of mineral raw materials, one can use the relative change in free surface energy associated with changes in the surface tension of powders and specific surface area during the grinding of raw materials or surface activity that determines the redistribution of the potential energy of the system in the macro-state and after the process of mechanical dispersion. A functional relationship between these criteria has been established, which is characterized by a linear dependence.