Real-Time Animal Location Estimation Using Wearable Sensors and Cellular Mobile Networks

Over the past decade, there has been a tremendous expansion of wearable sensor network domains to utilize the Internet of Things (IoT) potential. During their typical activities, wild animals usually form compact herds of con-species with close inter-herd proximity. Still, they frequently display a level of movement that could vary the spatial proximity under unpleasant conditions (e.g., pursuing prey or running from danger such as illegal hunters or poachers). As a result, wildlife monitoring systems (WMS) must identify various herd actions in real-time.

WMS applicants might be a good fit for them. While most IoT applications, such as smart cities [1-2] and industrial monitoring [3], rely on either short-range wireless technologies like Bluetooth [4], WiFi, or long-range wireless technologies like cellular to communicate among network devices, WMS imposes a diverse set of requirements. Radar, GPS, and satellite-based systems have already been used to track and monitor wild animals [5]. These alternatives, however, were less appealing due to their inherent high cost and severe connection delay. Some efforts have also been undertaken to construct WMS based on wireless sensor networks (WSNs), in which short-range wireless technologies (e.g., ZigBee) are used to form multi-hop mesh networks [6, 7]. Most of these systems are built on top of the IEEE802.15.4 standard [8], which has high overheads due to its sophisticated implementation and poor scalability [9, 10].

The method of wireless communications is based on weaker electromagnetic wave carrier transmissions through air channels to mobile equipment. The weaker signaling possibility may interrupt the continuous connection between transmitters and mobile user equipment. Therefore, the cellular towers need to know the accurate positions of their users to provide better service and smooth hand-over among towers. However, to avoid the interruption for continued service, cellular towers utilize a method called cell triangulation to know the approximated position of mobile users [11].

As an outcome, these service providers can provide location-based services to their customers, and this may help to improve criminal investigations of military aspects [3]. However, to smooth operations of the triangulation method required a supportive triangulation algorithm to improve the efficiency of the predicted position of mobile users.

Fortunately, new low-power wide-area network (LP-WAN) technologies such as LoRa, Sigfox, and others promise to provide improved coverage while consuming less energy, which meets many remote wildlife monitoring requirements applications [2, 11]. Among the LPWAN technologies, LoRa is thought to have the most potential for achieving LPWAN IoT goals. Lora is used in IoT applications that require a low data rate, low power, and a long-range. In general, LPWANs are built to provide highly extended battery life and smooth interoperability between end devices without the need for complicated local installs. However, because of the generic low bit-rate, harsher duty-cycle constraints, and larger packet header associated with LPWANs, IoT applications needing high data rate and low latency are not mainly the strength of LPWANs.

GPS technology has been used in outdoor animal tracking in [3-8], where a wearable GPS module has been attached to the animal's body and used a microcontroller to process the signal. The real-time location has been transmitted to the cellular network. One significant drawback in GPS is it can only obtain the x and y coordinates of the animal. If an animal is located on a slope, tree, etc., it won't provide accurate location information. Moreover, GPS consumes considerable power from its battery.

The proposed method is consisting a simple pressure sensor attached to the animal. The pressure values will be transmitted to the mobile base station. The geographical coordinates will be estimated based on our model. The proposed model has significant advantages, such as the system implementation cost is low as its using the already existing mobile network and a simple wearable sensor node; it consumes very low power and prolongs the batter lime time, and even this system can be implemented without a cellular network with modifications. Moreover, GPS-based systems have a significantly high error on-location estimation. Once the wearable sensor is worn in a natural field, it should run a considerable period without recharging.

• 2.    System Model

  • 2.1    Background

Here we are expected to derive a simple and accurate mathematical model, which leads us to a very accurate and reliable estimation of the location of an animal who lives in outdoor environments such as wild and farms. Further, this requirement can be achieved by using trigonometrical and physical properties belonging to electromagnetic waves and directional finding methods developed over the last century of wireless technology. Also, one can use the atmospheric properties of air to estimate the altitude of a position by measuring its pressure. This proposed model uses combinations of the above methods to predict an animal's accurate coordinates that attach a harmless transmitter for its life. Here, we are expected to know the altitude of the animal from sea level and find its location by knowing the direction of received electromagnetic waves and the traveling distance of the waves. For a clearer picture, let us assume that the system model of animals' position is indicated by Figure 1. Here, the point P(x,y,z) is the location of the animal and the point of receiving electromagnetic waves. The height of the antenna is H and Q represents the position of the receiving point of the signals from the transmitter attached to the animal body.

Fig. 1. System Overview

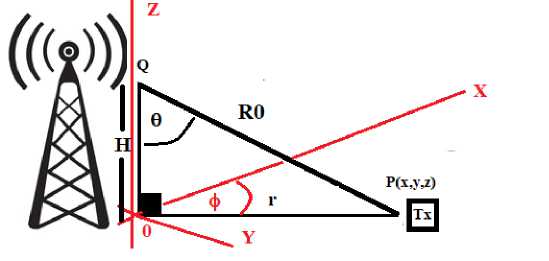
Let us assume that ht and hr are transmitter and receiver heights in terms of sea level. As shown below, let us assume that H gives the absolute height of the monitoring station's receiving antenna.

H = h r - h t

Also, the radial distance of the transmitter and receiver can be assumed to be R0, while one can measure this radial distance by assuming propagation time of electromagnetic waves Δt and magnitude velocity of light

R0 = CAt

Therefore, indicated r of Figure 1 can be easily computed by applying Pythagoras theorem as shown below.

r = ^H2- R02

Finally, by knowing the term r and assuming the direction of electromagnetic waves coming from to ϕ, we compute the position of an animal using the following equations.

X = ГС05ф у = Г51пф z = hr(6)

Using the above statements, one can accurately determine the point (x,y,z). However, the accuracy of this method may be heavily subject to the amount of accuracy for unknown parameters of hr, R, and ϕ. Therefore, we have to be chosen carefully selected methods to estimate these parameters for better results.

• 2.2    Methods of unknown parameter estimation

• 2.3    Principal behind the altitude measurements

• 2.4    Directional finding method of proposed system model

Here, we have three unknown parameters of h_r, R₀, and ϕ among the suggested system model. The measurement of these unknown parameters is estimated using the following method. First of all, a small transmitter attached to an animal (or group of animals) suggested sending the altitude h_r of the position at regular pulse intervals. Therefore, term H can be calculated by subtracting available receiver height h_t . Also, one can determine the radial distance R₀ between the transmitter and receiver by using half round trip time Δt between transmitter and receiver. Therefore, by estimating R₀ and H can estimate the parameter of measure r . Further, one can accurately measure the ϕ using existing methods refer to directional finding methods for radio waves.

One can assume the thermodynamics behind the atmospheric pressure to obtain a position's altitude. By applying the physics of thermodynamics, one can estimate the altitude of a position measure the pressure P. This estimation can be mathematically shown to the following equation below. In this equation, P0, T0 represents pressure and temperature at sea level. In contrast, R, L, M, and g represent the ideal gas constant, Laps rate, average mass of gas molecules, and gravitational acceleration.

h r = T_Q/b( 1-Q⁽^ )                               (7)

In this equation, the study of Laps rate L change has already been investigated, and those studies were conducted shows that Laps rate change in the atmosphere has a unique pattern [12-15]. Further, Laps rate change in range 0 to 15 Km has a linear relationship as shown in Figure 2.

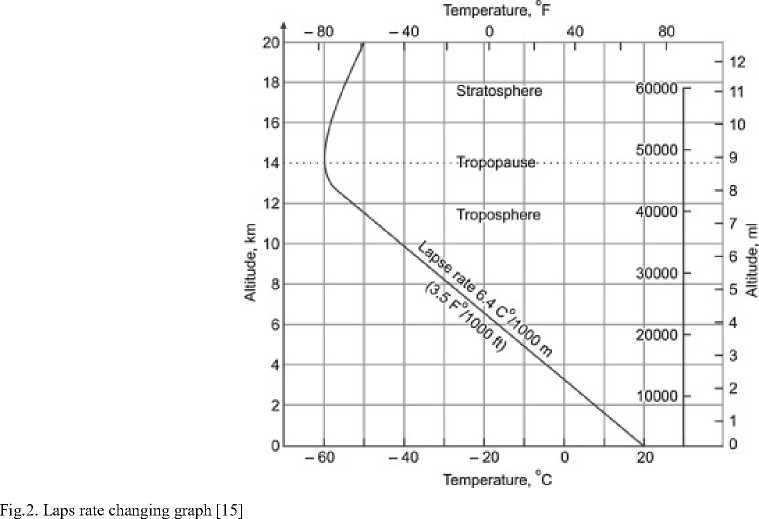
This unique behavior of Laps rate change allows us to use the above equation statement as accurate and straightforward altitude estimation relation to our purpose of the system model. In other words, the research conducted on lapse rate changes shows constant behavior for lapse rate below the Troposphere. Further, in the range of 0 to 15 Km, this value of laps rate has been experimentally confirmed to 6.4C0/Km [16-18]. Therefore, we can use an accurate pressure sensor attached to the transmitter to send a pressure reading to the receiver at the animal's position. Using the BMP280 pleasure sensor[19-20], we can directly convert pressure data to the corresponding altitude.

To estimate this system model's position accurately, one must require greater angle measurement accuracy for the direction of electromagnetic waves arrived. One degree of error is often required over the 2km of redial distance. Therefore, we used the correlative interferometer method of directional finding. Here this method can quickly implement with sufficiently large frequencies with minimum error profiles [21].

During this method, circular array antennas have been used to record the phase of the received waves about the predetermined conductor in the circular antenna array. In practice, this method uses an even number of metal conductors. The design and dimension of such an antenna array will depend on the required frequency in radio waves operated. Our directional finding can design an antenna array with smaller dimensions with slightly high frequencies.

Further, during this directional finding method, individually received phases of antenna arrey will correlate with the already pre-recorded phases of known directional angles and find direction for the maximum value of correlation comparisons as the original direction of electromagnetic waves coming. For an example, let us assume unknown incoming wave received phase reference to one of the conductors of a circular antenna array as the vector X= (x 1, x 2, x_3,…, x_n) and arbitrarily selected pre-recorded phrases recorded for the same reference conductor of the well-known angle of direction as Y= (y_1, y_2, y_3,…, y_n). Therefore, one set of correlation Comparison for n number of antenna conductors can be estimated as shown in the statement below with usual statistical notations [22-25].

S fc=i (X fc - x)(y_fc- у)

JS fc₌₁ (X k - х) ^{2 (} У к - У)²

Therefore, comparing different recorded vectors for different angle final direction of waves arrival can be obtained for maximum correlated value for X.

• 2.5    Error comparison with estimated positions

According to the proposed system model, there are many errors: radial distance measurement errors of R₀, altitude measurement errors of h_r, and directional finding errors of ϕ. Regarding radial distance measurement errors, this can be described as the case that radio waves have no direct line of cites with confirmed direction. Further, this error can explain as zero-mean half normal Gaussian probability distribution. Therefore, the average error of radial distance assumed to E R measurement can be computed as follow.

Er

TO

e-1^)2

R dR

Here, σ R is the standard deviation of error measurements, Also. This statement can be simplified as follow.

Er

-1(-)², E _1а²Г ^е ² = ^]

^ 2tt<7^{2           j}0         d.R

dR

Hence, average radial distance measurement error can be simplified as the statement below

^Er = a

In the case of altitude measurements with the BMP280 pleasure sensor, one can get a more accurate measurement of the altitude, and errors with this parameter can be ignored. However, it is equally probable to have errors in measured angle in both anticlockwise and clockwise directions with very small magnitudes in the directional finding method. Therefore, we assumed the error probability distribution as zero-mean Gaussian distribution with σ ϕ . Therefore, the average error E ϕ computation can be shown in the statement below.

1r ^ф

ЕФ = К ^”e 2Сф ф d<^                         (12)

\ ^2ка Ф    0

Here, using similar simplification steps done with the ER, the above statement of Eϕ can be simplified as the following statement below.

Еф = Оф\2

• 3.    Simulations and Results

We have simulated the proposed model considering different parameters such as pressure error (Pe), radial distance error (R e ), and directional finding angle error (P ϕ ) on location estimation.

In figure 3, it has been simulated different pressure errors (Pe) in Pascal. The uniform distribution of small error Pe has been simulated. It has been observed that when pressure error increase, the location estimation error also increases. Even in Pe=0.100, the error is less than 100m.

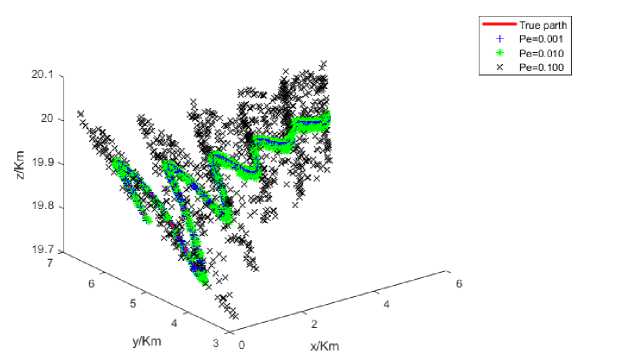
Fig.3. Location Estimation against different pressure errors (Pe)

Figure 4 shows the effect of directional finding error on-location estimation based on Gaussian distribution with the zero means. It observed that once the directional errors increase, location estimation errors also increase.

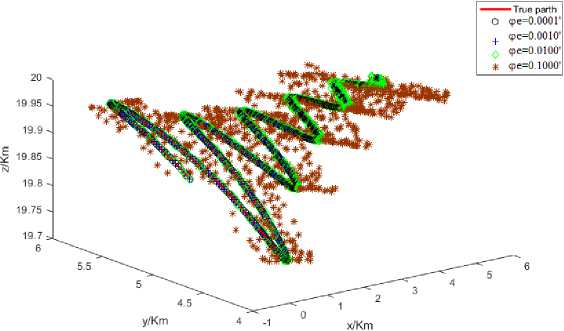
Fig.4. Location Estimation against directional finding angle ( Pϕ )

Figure 5 shows the effect of radial distance on-location estimation based on half-normal Gaussian distribution with the zero means. It observed that once the directional errors increase, location estimation errors also increase.

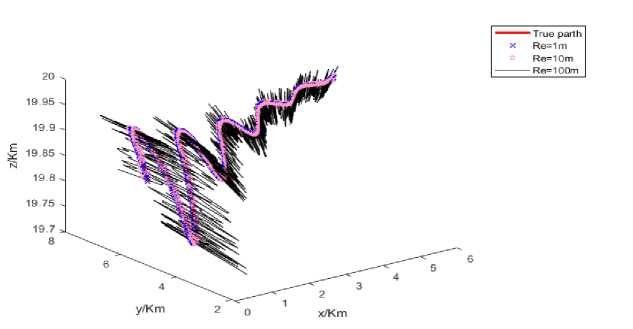
Fig.5. Location Estimation against radial distance(R e )

Figure 6 shows the simulation location against all three parameters, Pe, Re, and e. It has been observed that there is a high impact of directional error and radial distance error on the location estimation.

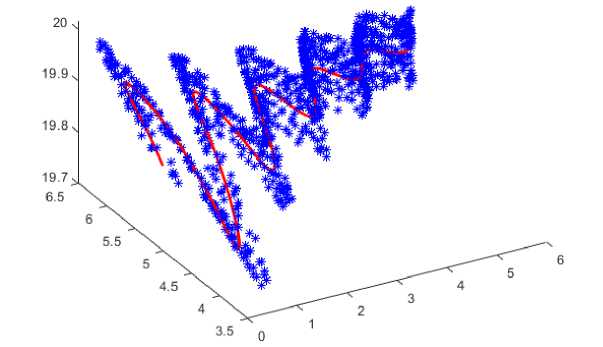
Fig. 6. shows the simulation location against all three parameters, P e , R e , and e.

• 4.    Conclusions

In this paper, we proposed a simplified, cost-effective, and accurate model to estimate the location of an animal that lives in outdoor environments. The proposed model is based on a simple geometric model using altitude calculation and the directional finding method. The model was analyzed under different parameters to understand the effect of those parameters on-location estimation. We validated the proposed model through simulations. The system model consists of a pressure sensor for altitude measurement. Based on analysis results, the error made by the pressure sensor seems to be negligible. The radial distance parameter has an error due to the reflection made by the obstacles. Therefore, the absolute value of radial distance cannot be measured. Hence, we assumed half-normal Gaussian distribution to analyze the error. Among the simulated parameters, directional finding angle(Pϕ) significantly impacts location estimation. Moreover, this error could vary around zero means. Therefore, we assumed zero-mean Gaussian distribution throughout the simulation.