Реализация алгоритма тестирования контекстносвободной грамматики на принадлежность классу LL(K)
Автор: Федорченко Л. Н.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Информационные системы и технологии
Статья в выпуске: 2, 2021 года.
Бесплатный доступ
В статье рассматривается алгоритм тестирования КС-грамматики в форме Бэкуса - Наура на принадлежность ее к подклассу LL(k) грамматик. Это наибольший «естественный» класс левоанализируемых грамматик, в которых левосторонний анализ может быть реализован детерминированным образом. Они допускают построение левостороннего вывода входной цепочки языка с использованием знания лишь о к впереди идущих символах. Такой анализ, в свою очередь, дает детерминированный метод определения выхода правильной трансляции. Рассматривается реализация основных свойств таких грамматик, как FIRST-FOLLOW-Sigma и алгоритм тестирования. В качестве языка разработки был выбран язык C#. Приложение реализовано на платформе .NET Core 3.1, позволяющей создавать программы для различных операционных систем. Тестирование кода осуществляется при помощи библиотеки XUnit, которая является одним из наиболее популярных решений для тестирования на платформе .
Контекстно-свободные грамматики, форма бэкуса, наура, алгоритм тестирования, ll(k) грамматики, функции first
Короткий адрес: https://sciup.org/148322213
IDR: 148322213 | УДК: 004.4 | DOI: 10.18101/2304-5728-2021-2-17-27
Текст научной статьи Реализация алгоритма тестирования контекстносвободной грамматики на принадлежность классу LL(K)
Одними из наиболее интересных, изучаемых и применяемых на практике свойств формальных грамматик являются те свойства, которые позволяют использовать эффективные методы трансляции языков. Среди грамматик с такими свойствами выделяется подкласс контекстносвободных грамматик — LL(к)-грамматики, наибольший класс левоана-лизируемых грамматик [1]. Они допускают построение левостороннего вывода входной цепочки языка с использованием знания лишь о к впереди идущих символах. Такой анализ, в свою очередь, дает детерминированный метод определения выхода правильной трансляции [2].
Таким образом, тестирование грамматики на принадлежность к классу LL ( к ) — это важная задача, решение которой позволяет облегчить построение транслятора.
Цель данной работы — реализовать алгоритм тестирования грамматики на принадлежность к классу LL.
1 Постановка задачи
Для достижения цели работы были сформулированы следующие задачи:
-
- провести обзор алгоритма тестирования КС-грамматики на принадлежность классу LL (к)-грамматик, приведенного в [1] и [2];
-
- реализовать алгоритм;
-
- реализовать пользовательский интерфейс;
-
- провести тестирование и отладку алгоритма.
-
2 ОбзорОпределения
Введем определения основных понятий, используемых при описании алгоритма.
Контекстно-свободная грамматика — четверка G = (V N , V T , P , S ), где V. , V T — непересекающиеся алфавиты соответственно нетерминалов и терминалов , P — конечное множество правил вида a ^ в , где a — нетерминал, а в — цепочка символов; S — начальный нетерминал.
Функция FIRST(k) — для цепочки символов a
FIRST k ( a ) = { w g V T :| w | < к и a =&> w или | w | = к | и a => wx ; x g V T *}
LL (k) грамматика — контекстно-свободная грамматика, такая, что
FIRST k ( pa ) П FIRST k ( ya ) = 0
для всех a , в , у , таких, что существуют правила A ^ в , A ^ у , в ^ у и существует левосторонний вывод S => wA a .
Операция © — для алфавита 2 и цепочек символов L 1 , L 1 с 2 *
L i © к L i {
w g 2 * к |x g L 1 , y g L 2, w =
xy , если I xy | < к FIRST ( xy ), иначе
Функция o ( A ) — для нетерминала A
o ( A )={ L c V Tk : 3 левосторонний S => wA a , w e V T , L = FIRSTk ( A ) }
Функция FOLLOW(k) — для цепочки символов в
FOLLOW k ( в ) = { w e V T : S =^ Yвa , w e FIRST k ( a )}.
-
3 Алгоритм тестирования LL(k)-грамматик
Алгоритм получает на вход контекстно-свободную грамматику и возвращает «да», если грамматика является LL(k )-грамматикой для целого к , и «нет» — иначе.
-
1. Вычислить функцию о ( A ) для всех нетерминалов, для которых существует более одного альтернативных правила.
-
2. Пусть A ^ в и A ^ у — различные альтернативные правила. Для каждого элемента L e о ( A ) вычислить
-
3. Если f ( L ) Ф 0 , то завершить алгоритм с результатом «нет».
-
4. Повторять предыдущие шаги для всех нетерминалов грамматики.
-
5. Завершить алгоритм с результатом «да».
f ( L ) = ( FIRST k ( в ) © к L ) n ( FIRST k ( у ) © к L ).
Алгоритм вычисления функции FIRST(k)
Для реализации описанного алгоритма необходимо сначала реализовать алгоритмы вычисления используемых в нем функций FIRST и о ( A ).
Поскольку (лемма 2.1 [2])
FIRST k ( в ) = FIRST k ( X 1 ) © к FIRST k ( X 2 ) © к - © к FIRST k ( X n ), достаточно вычислить значение функции для отдельных символов. При этом для терминалов и пустого предложения
FIRST ( X )= { X }.
Алгоритм основан на построении последовательных приближений функций F i ( X ) для всех символов X грамматики.
-
1. F i (a ) ={ a } для всех терминалов и любого i .
-
2. F 0( A ) = { x e V Tk : 3 A ^ x a e P , где | x | = к , или | x | < к и a = е }
-
3. Если F 0( A )... F _ , ( A ) уже построены для всех нетерминалов, то
-
4. Продолжать шаг 3, пока при некотором i = j не будет F j ( A ) = F j + 1( A ) для всех нетерминалов. Приближения являются вложенными множествами, поэтому рано или поздно такое произойдет.
-
5. Положить FIRST ( A ) = F j ( A ) .
F ( A ) = F _ i ( A ) и { x e V Tk : A ^ Vm e P , x e F _ i ( Y ) © к ... © к F - 1 ( Y m )}
Алгоритм вычисления функции σ(A)
Рассмотрим вспомогательную функцию о'( A, B) ={ L с VTk : 3 A =^ wBa, w e VT, L = FIRSTk (a)}
Так как о' ( S , B ) = о ( A ), то достаточно рассмотреть алгоритм вычисления о' ( A, B ).
Алгоритм основан на построении последовательных приближений О ( A , B ) для всех возможных пар нетерминалов грамматики.
-
1. о 0 ( A , B ) = { L с V Tk : 3 A > в B ae P , в , a e V\ L = FIRST k ( a )} .
-
2. Если о 0 ( A , B )••• a i '( A , B ) уже построены для всех пар нетерминалов, то положим
-
3. Продолжать шаг 2, пока при некотором i = j не будет o j ( A , B )= O y + 1 ( A , B )
-
4. Положить о' ( A , B ) = o j ( A , B ).
-
5. Положить о ( A ) = о' ( S , A ). Если {е} ^ о' ( S , S ), то a( S )=о'( S, S) и {{е}}.
О + 1 ( A , B ) = o i ( A , B ) и { L с V Tk : 3 A ^ X 1 X 2 ... X e P ;
для всех пар нетерминалов. Приближения являются вложенными множествами, поэтому рано или поздно такое произойдет.
С помощью данного алгоритма также может быть вычислена функция FOLLOW(k) для нетерминалов, поскольку
FOLLOW k ( A ) = |J L .
L eo ( A )
4 РеализацияИспользованные технологии
В качестве языка разработки был выбран C#. Данный язык позволяет перегружать операторы (например, оператор ’+’ для сентенциальных форм) и использовать функции LINQ (Language Integrated Query)1 для работы с последовательностями и множествами, что делает код более читаемым и понимаемым для человека.
Приложение реализовано на платформе .NET Core 3.1, позволяющей создавать программы для различных операционных систем и на разных операционных системах.
Тестирование кода осуществляется при помощи библиотеки XUnit, которая является одним из наиболее популярных решений для тестирования на платформе .NET.
Архитектура
Грамматики и составляющие их элементы представлены следующими классами (рис. 1):
-
1. GrammarSymbol — класс, представляющий символ некоторого алфавита, который имеет поле Literal, определяющее строковое представление символа.
-
2. Nonterminal — класс, представляющий нетерминал грамматики.
-
3. Terminal — класс, представляющий терминал грамматики.
SententialForm — класс, представляющий слово, составленное из нескольких символов (GrammarSymbol). Дает возможность работы со словом как с массивом символов (доступ по индексу). Также определены операторы ’+’ и ’==’, позволяющие складывать символы, получая экземпляр SententialForm, и сравнивать слова поэлементно. Пустое предложение ε представлятся как пустой экземпляр SententialForm.
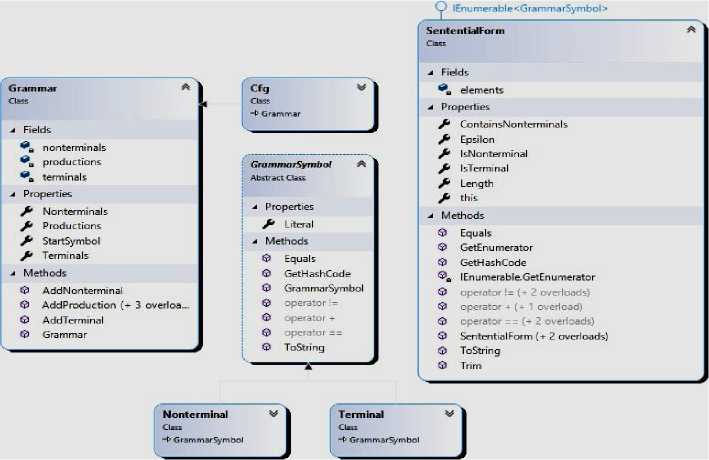
Рис. 1. Диаграмма классов грамматик и символов грамматик
-
1. Grammar — класс, представляющий формальную грамматику. Экземпляры этого класса имеют множества терминалов и нетерминалов, выделенный стартовый нетерминал и множество правил, представленных как пары экземпляров SententialForm.
-
2. Cfg — класс, представляющий контекстно-свободную грамматику. Отличается от Grammar тем, что позволяет добавлять только правила с одним нетерминалом в левой части.
-
3. LLkFunctionsLogic. Включает в себя реализацию функций FIRST( k ), σ( A ) и FOLLOW( k ). Соответствующие функции First, Sigma и Follow принимают грамматику, нетерминал (или слово в случае First) и число k как параметры.
-
4. LLkCheckerLogic. Имеет метод Check, принимающий в качестве параметров грамматику и число k , и определяет, является ли данная грамматика LL ( k ) грамматикой. Использует LLkFunctionsLogic.
Логика работы программы реализована в следующих классах (рис. 2):
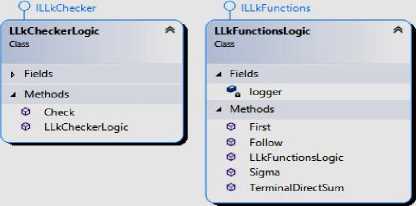
Рис. 2. Диаграмма классов, реализующих логику
Пользовательский интерфейс
Пользователь взаимодействует с приложением при помощи команд консоли (рис. 3). При запуске исполняемого файла в качестве аргумента командной строки передается путь к файлу с грамматикой, описанной в форме Бэкуса — Наура, например:
После запуска программы осуществляется разбор файла и генерация соответствующих экземпляров классов грамматики и символов. Затем полученные нетерминалы, терминалы и правила выводятся на экран и программа переходит в интерактивный режим, в котором доступны следующие команды:
-
■ First. Принимает число к , запрашивает у пользователя слово в алфавите грамматики, считает функцию FIRST ( k ) для него и выводит получившееся множество на экран.
-
■ Follow. Принимает число к , запрашивает у пользователя нетерминал грамматики, считает функцию FOLLOW ( k ) для него и выводит получившееся множество на экран.
-
■ Check. Принимает число к , осуществляет проверку, является ли грамматика LL ( k )-грамматикой, и выводит результат на экран.
-
■ Exit. Выход из программы.
Nonterminals:
SAB
Terminals: a b Start symbol:
S
Productions:
S -> a A a В
S -> b A b В
A - > a
A -> a b
В -> a
В - > a В
Commands:
first к --- calculate FIRSTk set for sentential form follow к --- calculate FOLLOW_k set for nonterminal check к --- check grammar for being LL_k exit --- exit from program
Enter command: first 1
Enter sentential form (use space as delimiters): В
FIRST_1 set for sentential form: a
Enter command: check 2
Grammar is not LL_2
Enter command: check 3
Grammar is LL_3
Enter command:
Рис. 3. Пользовательский интерфейс во время работы с программой
Фрагменты кода
Далее представлен исходный код реализации функций First, Sigma и Check.
Для построения последовательных приближений в функциях First и Sigma используется два экземпляра структуры данных HashSet — предыдущие приближения и строящиеся в данный момент. На каждой итерации происходит проверка этих множеств на равенство (функция DeepEquals), и в случае равенства происходит выход из цикла.
public HashSet
{ if (dimension ≤ 0)
{
-
throw new ArgumentException( ” Dimension must be a positive number. ” ) ;
} if (argument == SententialForm. Epsilon)
{
-
return new HashSet
() { SententialForm. Epsilon };
} foreach (var symbol in argument)
terminal))
{ throw new ArgumentException(”Terminal {terminal} in sententia is not from grammar.” ) ;
Contains(nonterminal))
{ throw new ArgumentExcep-tion(”Nonterminal {nonterminal} in sententia is not from grammar.” ) ;
}
} var approximations = new Dictionary >>(); var prevApproximations = new Dictionary foreach (var terminal in grammar. Terminals) { approximations[ terminal] = new HashSet SententialForm(terminal) }; } } foreach (var nonterminal in grammar. Nonterminals) { approximations[ nonterminal] = new HashSet foreach (var production in grammar. Productions. Where(p => p. left == nonterminal)) { var trimmed = production. right. Trim(dimension) ; if ( ! trimmed.ContainsNonterminals) { approximations[ nonterminal ] . Add(trimmed) ; } } } (рамки объёма статьи не позволяют привести полный текст программы) if (intersection. Count() > 0) { return false; } } } } } return true; } 5 Тестирование Алгоритм был протестирован на проверку как свойства LL(k), так и работы функций First, Follow и Sigma. Тестирование проводилось на нескольких грамматиках, для которых заранее были известны искомые свойства и значения функций (рис. 4). В результате программа была протестирована на 34 вариантах входных параметров для First, Follow и Sigma и 10 вариантах входных параметров для Check (рис. 5). private static Cfg grammarl = new CfgCS) .AddNonterminaL(A) .AddNonterminaL(B) .AddTerminaL(a) .AddTerminaLCb) .AddProductionCS, a + B) .AddProductionCS, b + A) .AddProductionCA, a) .AddProductionCB, b) .AddProductionCA, b + A +A) .AddProductionCB, a + В +В) .AddProductionCA, a +S) .AddProductionCB, b + S) as Cfg; private static Cfg grammar2 = new CfgCS) .AddNonterminatCA) .AddNonterminatCB) .AddTerminalCa) .AddTerminalCb) .AddProductionCS, a + A + a + B) .AddProductionCS, b + A + b + B) .AddProductionCA, a) .AddProductionCA, a + b) .AddProductionCB, a) .AddProductionCB, a + B) as Cfg; Рис. 4. Пример определения грамматики для тестирования Рис. 5. Оповещение об успешно пройденных тестах в среде разработки Visual Studio Заключение В результате работы достигнуты следующие цели: 1. Проведен обзор алгоритма тестирования КС-грамматики на принадлежность классу грамматик LL(k). 2. Алгоритм реализован в консольном приложении. 3. Проведены тестирование и отладка алгоритма.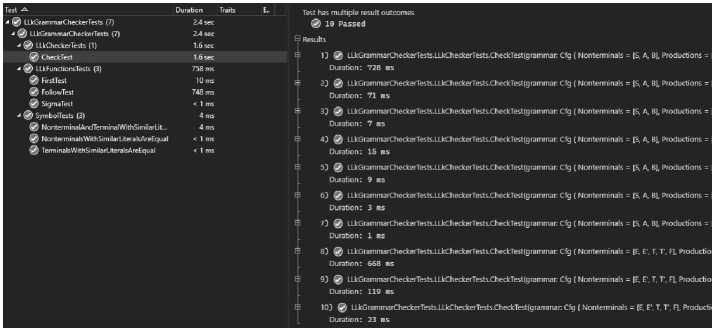
Список литературы Реализация алгоритма тестирования контекстносвободной грамматики на принадлежность классу LL(K)
- Aho Alfred V., Ullman Jeffrey D. The Theory of Parsing, Translation, and Compiling. USA, New Jersey, 1972. 562 р.
- Мартыненко Б. К. Языки и трансляции. Санкт-Петербург: Изд-во СПбГУ, 2013. 305 с. Текст: непосредственный.


