Реализация интерактивного дистанционного курса «Дискретная математика» в интеллектуальной e-learning системе «MathBridge»

E-learning система MathBridge в настоящее время в России мало известна. Лишь в нескольких высших учебных заведениях России реализованы учебные курсы на платформе MathBridge, тогда как в ведущих ВУЗах Европы (Университет Саарланда, Германия; Технологический Университет Тампере, Финляндия; Университет Клода-Бернара, Франция и др.) широко применяют этот инновационный продукт для создания собственных дистанционных курсов [1]. В Российской Федерации система Math-Bridge     внедряется в рамках Европейского образовательного проекта TEMPUS-MetaMath [2].

В отличие от широко применяемых в России программных сред обучения [3], система MathBridge позволяет реализовать практические компоненты обучения (упражнения, расчетные и графические задания и т.п.) без привлечения сторонних программных продуктов [4], что значительно увеличивает эффективность применения данной образовательной среды на практике.

Одним из первых дистанционных курсов, разработанных в системе MathBridge в технических ВУЗах РФ, является курс «Дискретная математика», читаемый во втором и третьем семестре для бакалавров специальности «Прикладная математика» в КНИТУ-КАИ.

Курс «Дискретная математика» включает в себя основные типы объектов системы, и позволяет глубоко оценить все преимущества среды MathBridge для разработки подобных курсов.

Структура курса «Дискретная математика»

Как описывалось в работе [5], курс в Math-Bridge собирается из отдельных физически независимых блоков, называемых учебными объектами. Учебным объектом может как лекция или тест в целом, так и любая их компонента: теорема, аксиома, определение, пример и т.п. Таким образом система Math-Bridge предоставляет возможность создавать модульные гибкие курсы, собираемые из отдельных объектов-блоков.

Курс «Дискретная математика» собран из двух типов учебных объектов -статических и динамических. Статические объекты включают в себя (Рис.1.):

• 1.    Аксиомы

• 2.    Методы

• 3.    Определения

• 4.    Текстовые документы (записки)

• 5.    Доказательства

• 6.    Утверждения

• 7.    Примеры

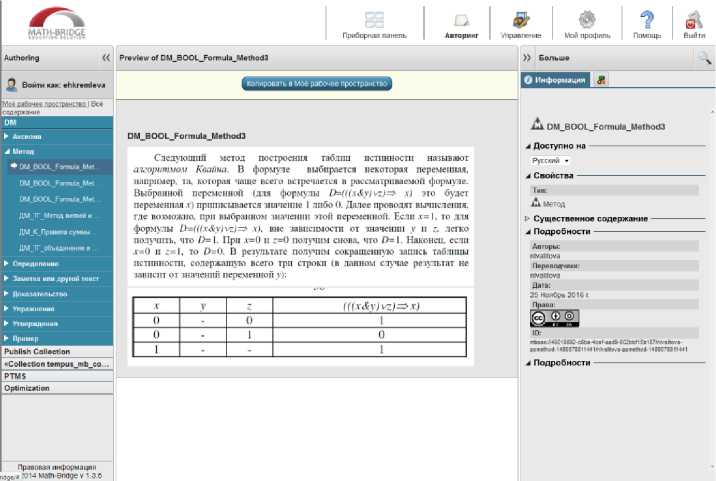
Рис. 1. Перечень учебных объектов дистанционного курса «Дискретная математика»

Динамические объекты представлены тестовыми упражнениями (Рис. 2.).

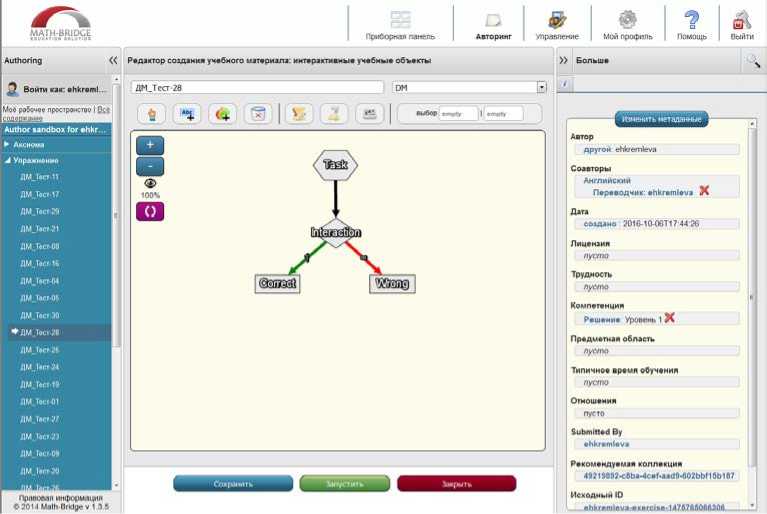
Рис. 2. Перечень тестовых упражнений дистанционного курса «Дискретная математика»

Курс состоит из двух учебных книг – книги, содержащей теоретический материал ( Рис.3. область 1), и книги, содержащей тестовые задания для проверки знаний (Рис. 3. область 2):

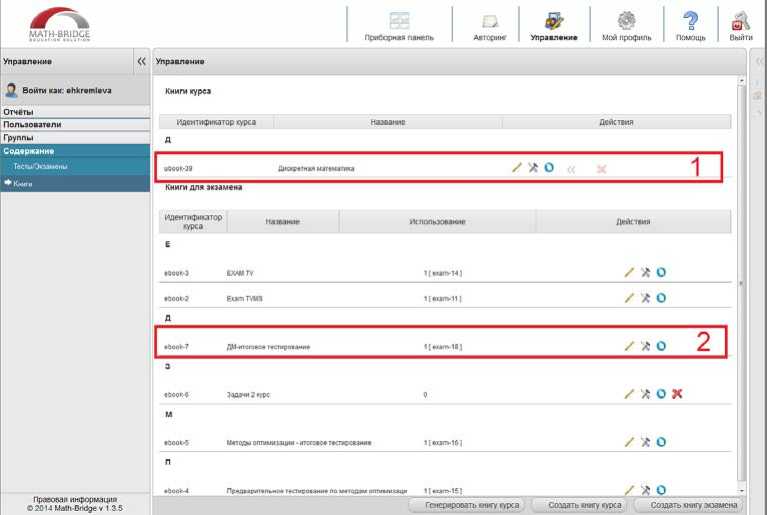
Рис. 3. Книги курса «Дискретная математика»

Книги являются модульным набором созданных учебных объектов (Рис.4-5.).

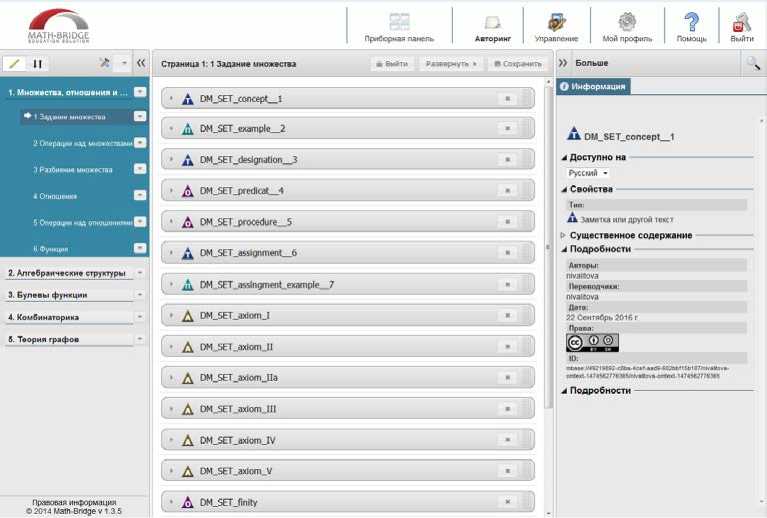
Рис 4. Структура и содержимое учебной книги курса «Дискретная математика»

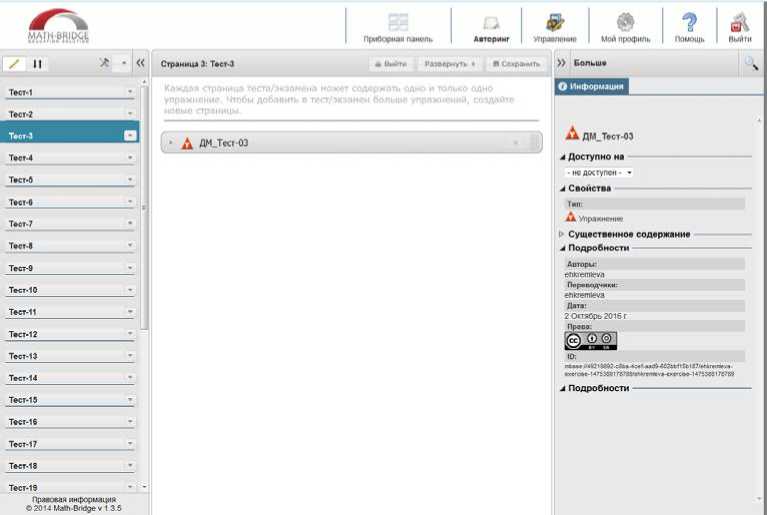
Рис 5. Структура и содержимое книги итогового экзамена курса «Дискретная математика»

Статические учебные объекты

Технология создания объектов статического типа включает в себя следующие возможности:

• 1.    задание имени и коллекции для объекта;

• 2.    ввод содержимого (контента) вручную;

• 3.    импорт данных из других программных пакетов. Доступна вставка рисунков, объектов GeoGebra и формул LaTeX;

• 4.    редактирование метаданных;

• 5.    перевод объекта на другой язык.

Для задания имени объекта необходимо ввести любое имя в поле ввода имени. Поле имени не может быть пустым. При попытке сохранения неименованного объекта на экране появится диалоговое окно с требованием ввести имя. Также в панели именования необходимо выбрать коллекцию, в которой новый объект будет опубликован. Учебные объекты включают в себя фактическое содержание, которое предоставляется студенту, но сами по себе они не могут отображаться. Учебные объекты становятся доступными только если они являются частью так называемой коллекции контента. Коллекция представляет собой пул объектов по принципу организации папок в Windows: как папка объединяет в себе отдельные файлы, так коллекция содержит в себе набор отдельных объектов. Установить коллекцию для опубликования можно выбрав одну из доступных коллекций из выпадающего списка рядом с полем ввода имени.

Ввод содержимого статических объектов Math-Bridge осуществляется простым набором текста внутри области ввода содержимого.

На Рисунке 6 представлен пример статического объекта типа «Определение» (область 1) с именем «DM_ALG_AlgSystemAlgebraModel_AlgSystem_Def» (область

2), созданного в коллекции DM (область 3) и содержащего описание алгебраической системы (область 4).

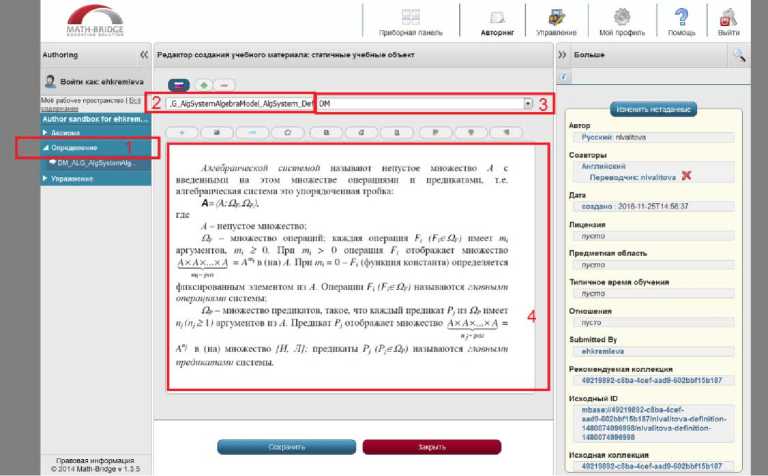
Рис. 6. Статический учебный объект курса «Дискретная математика»

Кроме добавления и редактирования содержимого статического объекта, система MathBridge позволяет редактировать его метаданные. Редактор метаданных всегда будет отображаться на вкладке с правой стороны (Рис. 7). Он отображает все открытому объекту

метаданные, которые в настоящее время соответствуют обучения.

Типичное время обучения пусто

Алгеораическо?! cucmeMofi называют введенными на этом множестве операциями! алгебраическая система это упорядоченная тропка:

А=(А: Йр.Йр).

А - непустое множество:

Й - множество операций: каждая операция F, (Р,еЙг) имеет пц аргументов, nif > 0. При т, > 0 операция F, отображает множество Ах Ах.,.х А = А"1' в (на) .4. При mj = 0- ^ (функция константа) определяется фиксированным элементом из .4. Операции Fj (Р^еДр) называются главными операциями системы:

Др - множество предикатов, такое, что каждый предикат Р, из Йр имеет п,(п;£1) аргументов из .4. Предикат Р, отображает множество АхАх^хА =

Отношения пусто

Правовая информация ©20i4Matn-endgev1.3 5

А"' в (на) множество (И. Л,: предикаты Pj (Р,ейр) называются главными предикатами системы.

Сохранить

Закрыть

Submitted By ehkremleva

Рекомендуемая коллекция

492l9892-c8ba-4cef-aad9-602bbfl5M87

Исходный ID mbaseJ/49219892-c8ba-4cef- аа d9 -60 2b bf 15Ы 87/nlval itova-defin ition-1480074996998lnlva1itova-definition-1480074996998

Исходная коллекция

49219892-c8ba-4cef-aad9-602bbf15b187

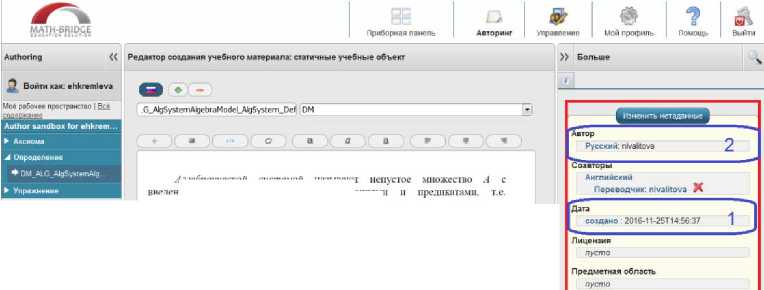
Рис. 7. Параметры метаданных статического объекта «Определение» курса «Дискретная математика»

Некоторые из метаданных уже установлены по умолчанию. Эти метаданные описывают неизменяемую информацию об учебном объекте, такую как время создания (Рис. 7. область 1) или имя автора (Рис.7. область 2). Эти поля не могут быть изменены. Для того, чтобы добавить больше метаданных, например, педагогическое или семантическое описание, редактор предоставляет мастер метаданных. Этот мастер всплывает в окне редактирования при нажатии кнопки редактора "Изменить метаданные" (Рис. 8.).

Шаг 1 -Выбрать тип русский nivaiitova

Отношения

► Аксиома ai Определение

’ DM_ALG_AJgSystemA)g.

* Упражнение с nivaiitova X

Author sandbox for ehkrem фиксированным элементом из Л. Операции F, (F,6f2F) называются главными операциями системы:

Й_Р- множество предикатов, такое, что каждый предикат Р, из J2_P имеет п, (ri)> 1) аргументов из Я, Предикат Р, отображает множество Дх Дх,,,хД =

Типичное время обучения пусто мое раоочее пространство i bee содержаний

Предметная область пусто

создано: 2016-11-25714:56:37

A"i в (на> множество {И. Л}; предикаты Р, <Р)еЯ_Р) называются главными предикатами системы.

Submitted By ehkremleva

Рекомендуемая коллекция

49219B92-c8ba-4cef-aad9-602bbf15M87

Сохранить

закрыть

Исходный ID mbase://49219892-c8ba-4cef- aad9-602bbf15b187Jnlvalitova-definlticn-1480074996998Znlvalitova-definitlon-1480074996998

Правовая информация ©2014 Math-Bridge vl 35

Исходная коллекция

49219892-c8ba-4cef-aad9-602bbf15b187

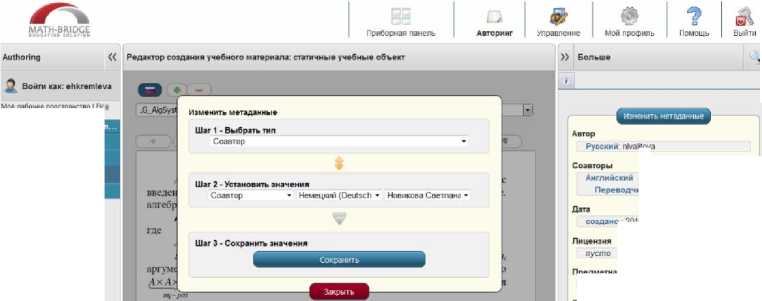
Рис. 8. Редактор метаданных

Редактор позволяет осуществить процесс добавления новых метаданных в 3 простых шага. Можно добавить любой объем метаданных, и затем нажать кнопку «Сохранить». Новые метаданные немедленно отображаются в окне редактора на правой стороне (Рис. 9.).

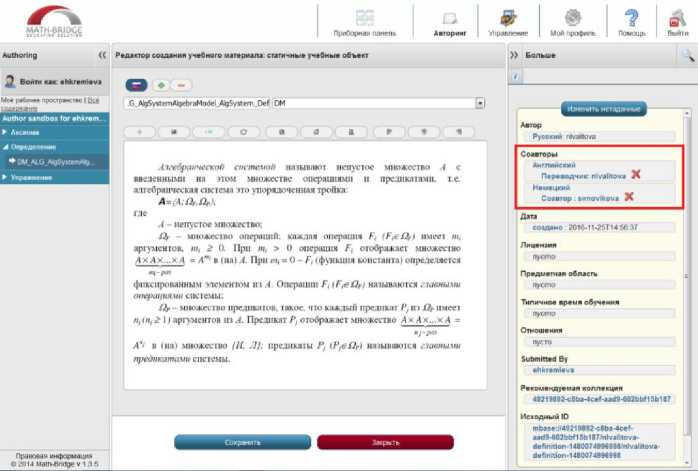
Рис. 9. Добавление в перечень метаданных информации о соавторе создания статического объекта

Если добавить метаданные, которые уже установлены для учебного объекта, вновь созданные метаданные заменят существующие.

Особый интерес представляют метаданные раздела «Отношения». Параметр «Отношения» необходим для того, чтобы созданное задание было способно автоматически проверять указанную компетенцию [6]. Для настройки параметра «Отношения» необходимо открыть объект в режиме редактирования и нажать на кнопку «Изменить метаданные» на панели метаданных в правой части окна редактора. У объекта, который не может использоваться для проверки компетенций, поле «Отношения» пусто (Рис.10.):

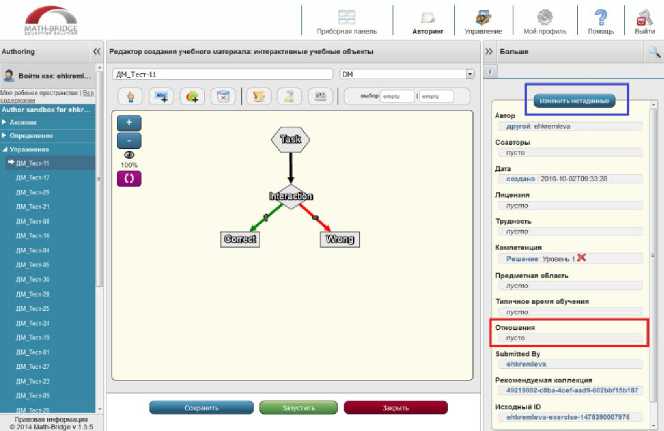
Рис. 10. Интерактивный учебный объект типа «Упражнение», непригодный для оценки уровня усвоения компетенций

В открывшемся окне «Изменить метаданные» на первом шаге следует выбрать тип изменяемых метаданных – Отношения (Рис.11.):

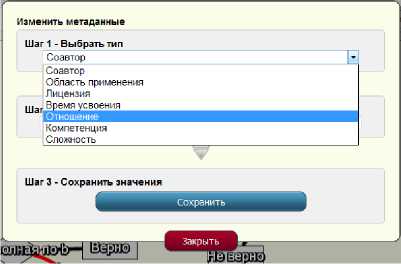
Рис. 11. Выбор типа редактируемых метаданных

На следующем шаге – Установить значения – следует выбрать значение «Учит» (Рис.12.):

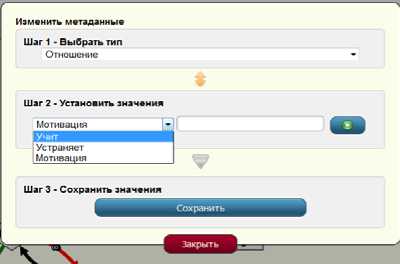
Рис. 12. Выбор значения для метаданных «Отношения»

После чего необходимо в свободном поле справа описать компетенции, проверяемые данным упражнением. Список всех компетенций доступен по нажатию на кнопку справа от поля для ввода. Компетенции, представленные в списке, соответствуют образовательным стандартам Европейского общества инженерного образования SEFI, которые являются на сегодняшний день образцом для составления компетенций в отечественном образовании [7]-[9].

Список компетенций организован в виде иерархической структуры «Уровень усвоения-Учебный курс- Тема - Компетенция» (Рис.13.).

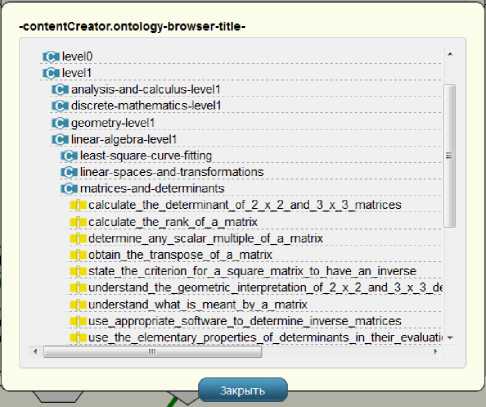
Рис. 13. Выбор конкретной компетенции, проверяемой при помощи созданного упражнения

Нажав кнопку «Сохранить», выбранная компетенция будет добавлена в список компетенций, проверяемых данным упражнением. Таким образом можно добавить несколько компетенций, то есть одно и тоже упражнение будет способно оценивать овладение различными компетенциями (Рис.14.).

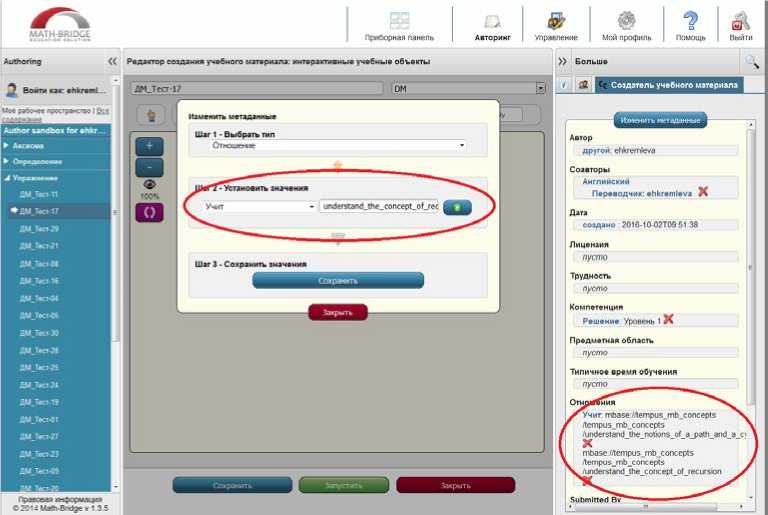
Рисунок 14. Добавление к учебному объекту метаданных, позволяющих оценивать две выбранные компетенции

Динамические учебные объекты

Динамические объекты в дистанционном курсе «Дискретная математика» представлены в основном одношаговыми тестовыми заданиями с несколькими вариантами ответов. Согласно концепции MathBridge, динамические объекты представляются в виде аналогов блок-схем, за счет чего реализуется возможность гибкого многошагового интерактивного взаимодействия с обучаемым. Типичная структура теста для курса «Дискретная математика» представлена на рисунке 15.

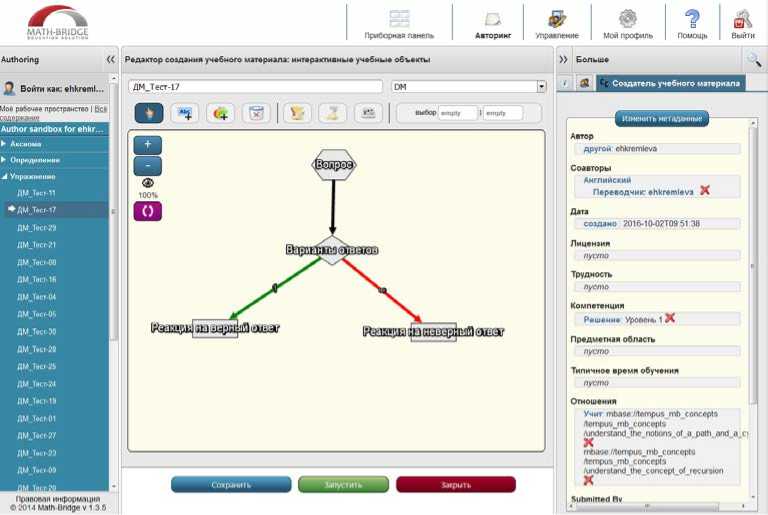
Рис. 15. Схема динамического объекта-теста курса «Дискретная математика»

Создание динамических учебных объектов можно рассматривать как создание множества статических объектов, которые представлены в определенном порядке, определяемом блок-схемой задания.

Набор инструментов для создания динамических объектов

Панель инструментов для создания динамических объектов содержит все необходимые для создания динамического объекта обучения инструменты.

Кроме этого в правой части панели дается обзор текущего выбранного инструмента и шагов. Щелкнув левой кнопкой мыши по этому обзору можно сбросить выбранный инструмент и шаги. На панели инструментов располагаются следующие инструменты (рисунок 16 - слева направо):

• •    Выбор : Выбор шага или перехода для просмотра и / или редактирования его микроструктуры.

• •    Добавить шаг : Добавляет новый шаг к макро-структуре, который затем можно редактировать с помощью выбора инструмента.

• •    Добавить переход : Добавляет новый переход к макро-структуре, который затем можно редактировать с помощью выбора инструмента, если это условный переход.

• •    Удалить : Удаляет шаг или переход по щелчку левой кнопкой мыши.

• •    Описание упражнения : Добавить приглашение или описательный текст в упражнение, которое было показано в окне предварительного просмотра.

• •    Добавить шаблон упражнения : Добавляет заранее определенный набор шагов и переходов на упражнения. Доступны различные шаблоны, которые могут быть выбраны в диалоге.

  • Параметры упражнения : Управление параметрами для упражнений. Параметры позволяют создать упражнения, которые используют не фиксированные значения, а переменные для задач и условий перехода.

  

  Рис. 16. Панель инструментов создания динамических объектов

  
  

Всего курс «Дискретная математика» содержит 30 подобных упражнений-тестов.

Сборка и опубликование курса

После того, как учебные объекты были созданы, каждый из них был опубликован, то есть предоставлен всем разработчикам других курсов в свободное пользование. Только после опубликования объект может быть добавлен в книгу, которая, в свою очередь будучи опубликованной, станет доступной для изучения студентов.

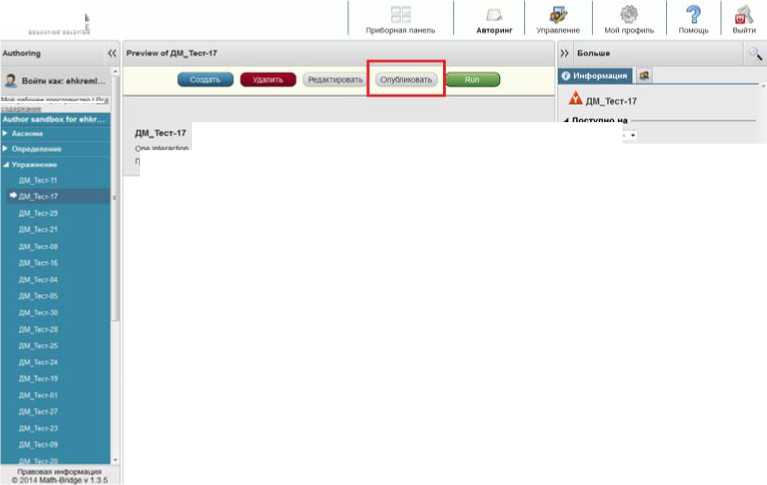
Для опубликования любого учебного объекта, статического или динамического, необходимо сохранить объект, выйти из режима его редактирования и нажать на кнопку «опубликовать» на панели управления объектами (Рис. 17):

доступно не д Свойстве

Author r>g DMa one wweracoon ячме ететсве

Греф о «лором есть и дут* и ребра намается

А yTViWWfW

Существенное содержание а Подробности а Подробности

Sutwniticd by         [и$ет 'ehuerrerva" (Кремлееа Элмир

Original id            ct*ze«Twva-c»cfcisc-i47S30l0087ll

Original collection      DM

Suggested cotecton DM

Рис. 17. Опубликование объекта-теста

MATHBRIDCt

Мое pebwee простренепо I Utt

Объект исчезнет из авторского рабочего пространства разработчика (переключатель «Моё рабочее пространство»), но появится в общем рабочем пространстве (переключатель «Все содержание») в указанной при создании объекта коллекции (Рис. 18). При этом объект будет помещен в раздел, соответствующий его типу (упражнение, аксиома, определение и т.п.).

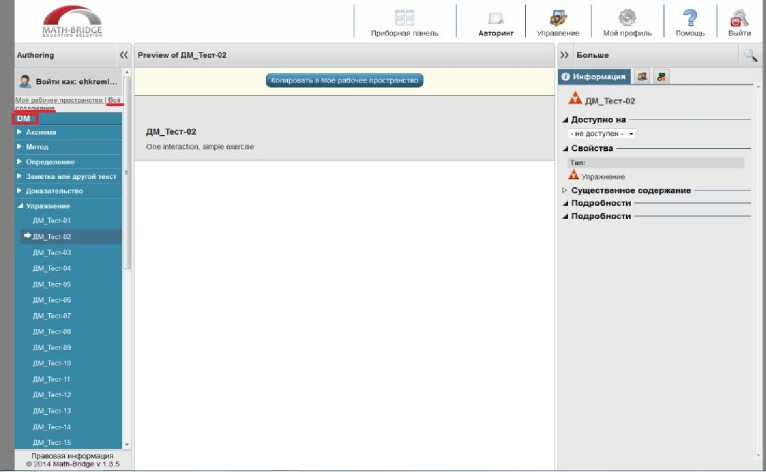
Рис. 18. Опубликованные в разделе «Упражнения» коллекции DM тесты

Далее, перейдя в режим Управления, были созданы книги для теоретического материала и тестовых заданий на экзамене, куда затем были скопированы опубликованные ранее объекты (Рис. 19).

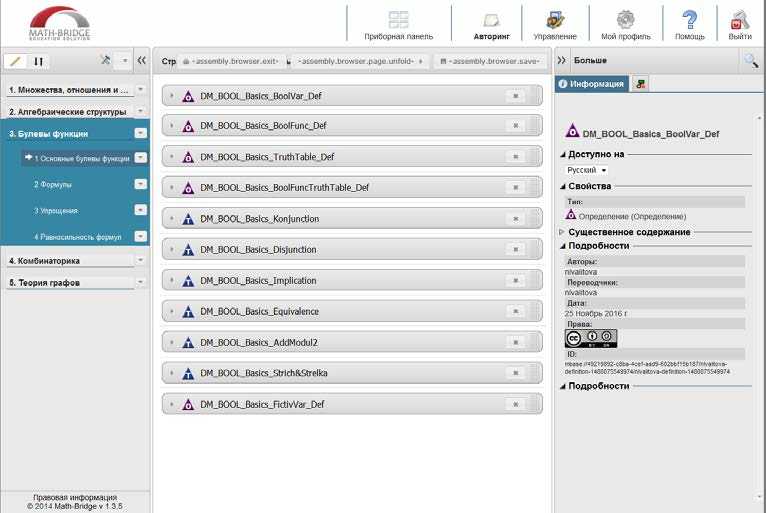
Рис. 19. Пример собранной страницы раздела «Булевы функции» теоретической книги курса «Дискретная математика»

Для опубликования книги необходимо перейти в режим Приб орн ой панели и в окне

«Мои курсы» напротив созданной книги нажать на кнопку - «опубликовать» (Рис. 20).

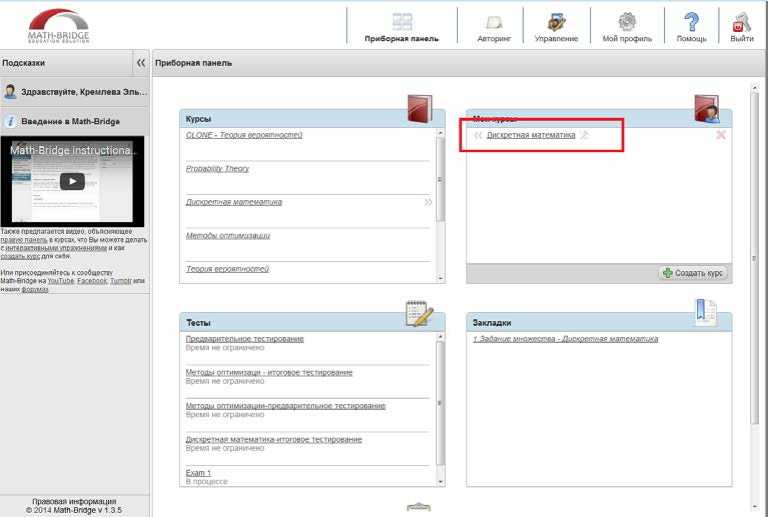
Рис 20. Книга курса «Дискретная математика» на Приборной панели

Теперь курс доступен для изучения (Рис.21.). Курс реализован на русском языке, хотя система MathBridge позволяет представлять учебные объекты более чем на 10 языках [10].

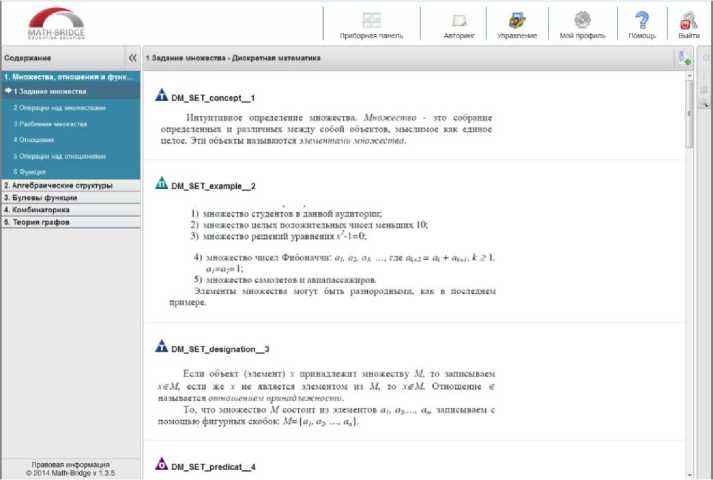
Рис. 21. Представление курса «Дискретная математика» студентам

Дистанционный курс «Дискретная математика» был разработан преподавателями кафедры Прикладной математики и информатики Казанского национального исследовательского технического университета им. А.Н. Туполева-КАИ под непосредственным руководством специалистов Немецкого Научного Центра Искусственного Интеллекта (DFKI) и в настоящее время внедряется в учебный процесс КНИТУ-КАИ для обучения бакалавров.

Данный проект профинансирован при поддержке Европейской Комиссии в рамках программы Темпус (№ гранта: 543851-TEMPUS-1-2013-1-DE-TEMPUS-JPCR). Эта публикация отражает исключительно взгляды авторов. Комиссия не несет ответственности за любое использование информации, содержащейся здесь

This project has been funded with support from the European Commission.

This publication [communication] reflects the views only of the author, and the Commission cannot be held responsible for any use which may be made of the information contained therein.