Реализация итерационных методов решения систем линейных уравнений в задачах математической физики на реконфигурируемых вычислительных системах
Автор: Левин И.И., Дордопуло А.И., Пелипец А.В.
Рубрика: Вычислительная математика
Статья в выпуске: 4 т.5, 2016 года.
Бесплатный доступ
В статье рассматриваются характерные особенности реализации итерационных методов решения систем линейных уравнений в задачах математической физики на параллельных вычислительных системах, которыми являются геометрическая декомпозиция расчетной области и распараллеливание данных внутри последовательно выполняемых процессором итераций с интенсивным информационным обменом между процессорами и памятью. Стандартные методы реализации итерационных методов решения систем линейных уравнений при множественных транзакциях с памятью и межпроцессорных обменах, существенно снижающих реальную производительность, дополнительно требуют от вычислительной системы наличия большого числа физических линий связи для реализации сложных топологий и иерархических схем хранения данных. Выходом является использование многопроцессорных систем с реконфигурируемой архитектурой, позволяющее адаптировать свою архитектуру под структуру итерационных алгоритмов математической физики путем распараллеливания по итерациям. В статье рассмотрена реализация метода Якоби для решения краевой задачи Дирихле для уравнения Лапласа на реконфигурируемой вычислительной системе, на примере которой показано сокращение количества внешних каналов обмена как одного из наиболее критических ресурсов реконфигурируемой вычислительной системы.
Реконфигурируемые вычислительные системы, программируемые логические интегральные схемы, численные методы математической физики, распараллеливание по итерациям, вычислительный конвейер
Короткий адрес: https://sciup.org/147160607
IDR: 147160607 | УДК: 004.382.2 | DOI: 10.14529/cmse160401
Текст научной статьи Реализация итерационных методов решения систем линейных уравнений в задачах математической физики на реконфигурируемых вычислительных системах
В процессе численного решении модельных уравнений математической физики часто возникает необходимость нахождения неизвестных в системах линейных алгебраических уравнений (СЛАУ) высокого порядка (для числа уравнений n > 1000). В данных условиях прямые методы, такие, как метод исключений Гаусса, могут быть неэффективны из-за высоких требований к оперативной памяти, большой вычислительной трудоемкости и накопления ошибок округления [1]. Поэтому предпочтительными становятся итерационные методы, которые позволяют найти приближенное решение СЛАУ за конечное число итераций, количество которых зависит от требуемой точности.
Параллельная форма реализации итерационных методов решения СЛАУ основана на концепции геометрического параллелизма, при котором исходная расчетная область, описывающая состояние физической среды в определенных точках пространства, разбивается по одному или двум пространственным направлениям с последующим распределением подобластей между процессорами. Ключевой особенностью реализаций итерационных методов на параллельных многопроцессорных системах является то, что итерации выполняются последовательно, а распараллеливание задачи происходит по данным на уровне вычислений внутри итерации [2]. При этом каждый процессор обрабатывает свою часть области в течение всех итераций, обмениваясь результатами с другими процессорами и с внешней оперативной памятью.
Однако необходимость интенсивных взаимодействий типа процессор-процессор и процессор-память сопряжена с большими накладными расходами, порой сводящими на нет весь эффект от распараллеливания. Особенно актуальной эта проблема становится по мере увеличения масштабов многопроцессорных систем и количества компонентов, входящих в них [3].
На параллельных вычислительных системах с «жесткой» архитектурой способы решения данной проблемы, в основном, сводятся к выбору подходящей топологии и организации системы хранения данных в виде сложной иерархической структуры. Это, в свою очередь, порождает проблему дефицита каналов памяти для обеспечения доступа к различным уровням иерархии.
Для решения указанных проблем активно проводятся исследования, связанные с поиском способов ускорения решения СЛАУ итерационными методами на высокопроизводительных системах. Работа [4] описывает применение гибридной версии технологий параллельного программирования OpenMP–MPI для сокращения накладных расходов вычислений в задачах механики жидкости методом конечных элементов. В статье [5] делается обзор опыта применения графических ускорителей для решения итерационными методами разреженных систем линейных уравнений, приводится сравнение эффективности реализаций алгоритмов на GPU NVIDIA TESLA с CPU Intel Xeon, использующим специализированные библиотеки линейной алгебры Intel MKL. Публикация [6] посвящена асинхронным итерационным алгоритмам, позволяющим уменьшить коммуникационные расходы по сравнению с другими алгоритмами, за счет устранения простоя узлов из-за ожидания синхросообщений. Приведенные экспериментальные результаты показывают, что модифицированный релаксационный метод Саусвелла уменьшает затраты на коммуникации по сравнению с другими асинхронными итерационными методами и классическим синхронным методом Якоби. Множество работ касаются использования гетерогенных вычислительных архитектур в решении разреженных СЛАУ итерационными методами. В частности, вопросам построения адаптированных итерационных алгоритмов, эффективно распределяющих вычислительную нагрузку в системах CPU-GPU, посвящены статьи [7–9].
В настоящее время альтернативой традиционным многопроцессорным архитектурам при решении задач математической физики все чаще выступают реконфигурируемые вычислительные системы (РВС), построенные на основе программируемых логических интегральных схем (ПЛИС) [10]. Здесь также проблема дефицита внешних каналов обмена является весьма актуальной, поскольку удельное количество пользовательских выводов относительно логической емкости кристалла снижается в каждом поколении
ПЛИС [11–13]. Применение различных методов распараллеливания по данным лишь усугубляет эту проблему.
«Гибкая» архитектура РВС позволяет, не меняя исходный алгоритм задачи, адаптировать вычислитель под ее информационную структуру, что дает возможность организовать для матричных задач не только геометрическое распараллеливание (по данным), но и временное (по итерациям). Это ведет к существенному сокращению количества внешних каналов обмена, являющихся одним из наиболее критических ресурсов реконфигурируемой вычислительной системы.
Целью данной работы является разработка и исследование алгоритма решения на РВС систем линейных алгебраических уравнений методом Якоби для матриц специального вида в задачах математической физики. В разделе 1 настоящей статьи дается описание преобразования краевой задачи Дирихле для уравнения Лапласа для решения ее в структурно-процедурной форме. В разделе 2 анализируются практические результаты решения на РВС краевой задачи Дирихле для уравнения Лапласа, приводится сравнение полученных результатов с реализацией данной задачи на параллельной кластерной системе. В заключении обсуждаются перспективы применения реконфигурируемых систем для решения систем линейных уравнений итерационными методами в задачах математической физики и указываются направления дальнейших исследований.
1. Преобразование в структурно-процедурную форму краевой задачи Дирихле для уравнения Лапласа
Рассмотрим в качестве примера решение задачи Дирихле для уравнения Лапласа, которое используется для описания различных стационарных (установившихся) физических процессов [14]. Пусть требуется решить задачу Дирихле для уравнения Лапласа, имеющего общий вид Δu(x,y,z) = 0, которое задано в двумерном пространстве диффе- ренциальной формой д 2 u д 2 и
дx 2 + ду 2
где u ( x,y ) – функция с граничными условиями первого рода, значение которой необходимо вычислить.
Тогда в результате дискретизации уравнения (1) методом конечных разностей на квадратной координатной сетке 07 согласно пятиточечному шаблону получим разностную (алгебраическую) форму ui+1, j — 2uij + ui-1, J h 2
U — 2 Uj, + U
-^j + 1---- J---,J — 1 = 0, (2)
h 2
шагом h = 1 , то поскольку порядок системы
где i,j = 1, 2, …, N -1;
h – постоянный шаг сетки, hN = 1.
Если построить сетку с постоянным равен n = (N-1)2, получим систему из 81 уравнения, которую можно последовательно решить методом Якоби с помощью формулы общего вида
„ (к+1) 1 к . „ к . к .к ulJ = 4(Ui+1,J + U.—1,J + U-.J+1+UI,J—1>’ (3)
где k – номер итерации.
Общая формула (3) эквивалентна системе линейных уравнений
|
к + 1 u 11 = |
2 4 ( uk 1 + u 01 + u 12 + u W ) |
|
u k ?1 = |
= 4 ( u k 2 + u k 2 + u 1 k 3 + u n ) (4) |
|
u 99 ' = |
2 4 ( uk 0,9 + uk 9 + u 9 k ,10 + uk 8 ) |
Исходя из того, что значения функции u ( x,y ) на границе рассматриваемой области известны заранее, система (4) может быть преобразована к виду
Y - константное значение множителя, у = 1 .
Итерационных процесс вычислений завершается при выполнении условия
| u ij — u tj I - £ , (6)
где ε – это требуемая точность.
Система (5) позволяет отобразить процесс вычислений неизвестных u ij на k +1 - ой итерации в виде полного информационного графа β, представленного в параллельном виде на рис. 1. Здесь информационные вершины соответствуют множеству исходных данных и результатов, операционные вершины изображают операции с данными, а дуги показывают направления информационного обмена между вершинами.
Особенности граничных условий первого рода определяют количество и порядок информационных дуг, соединяющих информационные вершины-источники с операционными вершинами-приемниками, а именно: адресные вершины (u^, ukn—1, uN-ц, uN—i n-1), соответствующие точкам, примыкающим к границе в углах области решения, соединяются с операционными вершинами-приемниками двумя дугами.
Адресные вершины u i k j , соответствующие точкам, примыкающим к границе области (исключая угловые точки ( u ^, u ^ n — 1 , u N -ц, u N - 1 n - 1 », соединяются с операционными вершинами-приемниками тремя дугами. Адресные вершины u i k j , соответствующие остальным точкам внутри области, имеют по четыре исходящих дуги. Адресные вершины сi j , соответствующие граничным точкам области решения (заданные значения функции), имеют по одной исходящей дуге.
Схема информационных зависимостей вершин, соответствующих узлам сетки внутри области решения, проиллюстрирована на рис. 2.
В пределах одной итерации информационный граф параллельной формы данной задачи можно рассматривать как кортеж информационно-независимых подграфов ( a k 1 , a k 2 ,..., a k n ) . Информационная независимость подграфов a i определяется отсутствием дуг, соединяющих операционные вершины двух или более подграфов в кортеже.
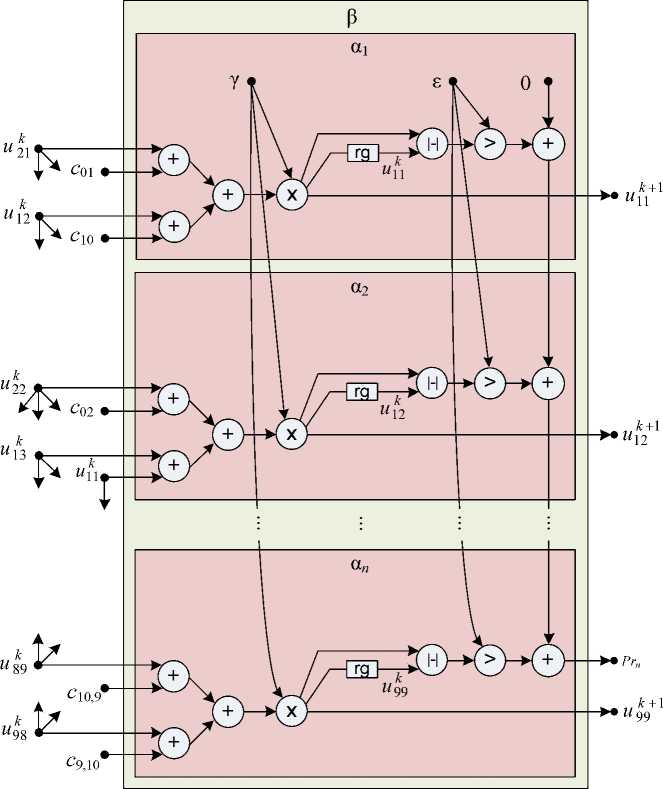
Рис. 1. Параллельная форма метода Якоби решения уравнения Лапласа
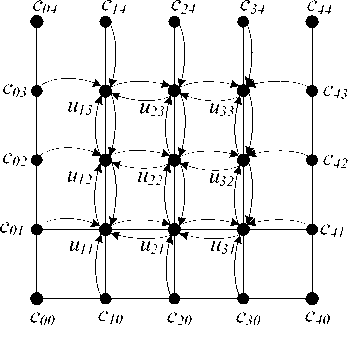
Рис. 2. Схема информационных зависимостей вершин, соответствующих узлам сетки
с шагом h =
В соответствии с пятиточечным шаблоном каждый из n изоморфных информационных подграфов αi на (k+1)-й итерации реализует одно умножение и три сложения операндов для получения на выходе очередного узлового значения функции uk+1. Кроме этого, операции модуля разности, сравнения и суммирования реализуют процедуру проверки условия сходимости (6), результатом которой является предикат Prn. Управляющая программа останавливает вычислительный процесс при обнаружении предиката, значение которого говорит о выполненном условии сходимости.
Общее число операционных вершин полного графа β параллельной формы для решения n систем уравнений будет составлять 7 n . Если бы количество итераций, которые необходимо пройти до завершения процесса вычислений, было известно заранее (например, m ), то алгоритм мог быть представлен в абсолютно-параллельной форме с числом базовых подграфов, равным n · m . Но поскольку необходимое количество итераций изначально не определено и зависит от выполнения условий сходимости, то число информационных подграфов в параллельной форме равно размерности матрицы n , а количество реализованных ими итераций может быть произвольным. Промежуточные результаты итерации k , являющиеся исходными данными для итерации ( k +1), должны записываться и считываться из внешней оперативной памяти.
Количество аппаратного ресурса для реализации параллельной формы задачи рассчитывается по формуле
A = n • N( a i ) , (7)
где N(α i ) – количество ресурса, необходимого для реализации базового информационного подграфа αi .
Реализация параллельной формы метода Якоби (рис. 1) возможна при наличии в вычислительной системе количества процессоров, достаточного для параллельной обработки всех узлов координатной сетки ш . Из (7) следует, что структурная реализация параллельной формы задачи требует наличия 7n процессорных элементов и 5n внешних каналов обмена. Для систем уравнений больших размерностей необходимый ресурс может превосходить параллельные возможности аппаратуры. В этом случае необходимо перейти от параллельной к структурно–процедурной (кадровой) форме вычислений и провести редукцию производительности путем сокращения числа подграфов, операционных и адресных вершин. При переходе к кадровой форме в результате векторизации подмножества информационных вершин представляются в виде адресных вершин– массивов G, функция которых состоит в генерации потока адресов обращения к памяти, где хранятся массивы обрабатываемых данных (результатов), а также вывод операндов в вычислительные устройства.
Пусть L – общий объем аппаратного ресурса вычислительной системы, такой, что
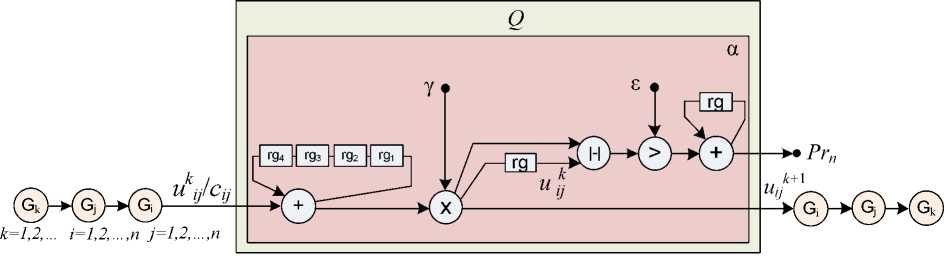
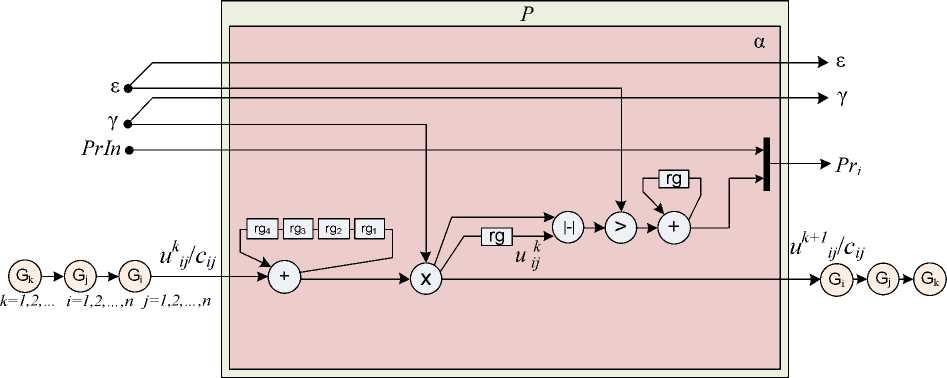
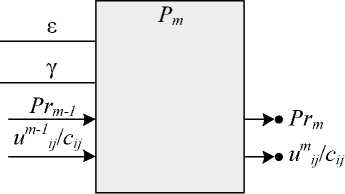
L A L Если аппаратного ресурса вычислительной системы достаточно для структурной реализации не более, чем r базовых подграфов αi, то кадровая форма задачи может быть получена путем сокращения полного графа β в n раз. Степень редукции производи-r тельности по подграфам [15] определяется возможностью структурной реализации определенного числа базовых подграфов в теле кадра. Предельным случаем редукции по подграфам является кадр Q, состоящий из одного базового подграфа α (рис. 3). При этом вычислительный процесс расчета узловых значений функции на текущей итерации (k+1) будет представлять собой циклическое (от 1 до n) выполнение кадра с получением Рис. 3. Кадровая форма метода Якоби решения уравнения Лапласа, состоящая из одного базового подграфа Особенностью данного кадра является то, что выходом адресных вершин–массивов G являются как вычисленные на предыдущей итерации узловые значения функции uikj , так и граничные значения cij, представляющие собой константы. И константы, и найденные приближения сеточной функции хранятся в одном массиве внешней опера- тивной памяти, в котором обновляются только значения u k+1 ij , вычисленные на текущей итерации. Дальнейшая редукция производительности путем сокращения функциональных устройств базового подграфа αi может быть осуществлена путем замены трех вершин суммирования значений функции на одну, где сложения будут производиться последовательно. Это позволит не только сократить аппаратные затраты на функциональные устройства, но и уменьшить количество внешних коммуникационных каналов. В данном случае число операционных вершин базового подграфа было сокращено с семи до пяти, а количество внешних каналов уменьшилось вдвое – с шести до трех (рис. 4). Особенностью разностной аппроксимации оператора Лапласа на пятиточечном шаблоне является то, что каждое уравнение системы (кроме точек, примыкающих к граничным областям) содержит пять неизвестных, используемых для нахождения приближенных значений uij функции u(x, y) в узлах двумерной сетки (xi,yj). Поэтому обратная связь накапливающего сумматора в базовом подграфе содержит четыре регистра rg для хранения промежуточных результатов суммирования. При аппроксимации на шаблонах, содержащих большее число точек, количество регистров в обратной связи накапливающего сумматора должно быть соответственно увеличено. Рис. 4. Кадровая форма метода Якоби решения уравнения Лапласа с предельно сокращенным числом базовых подграфов и операционных вершин Кадровая форма задачи может состоять как из нескольких, так и из одного предельно редуцированного базового подграфа. Выбор реализации, состоящей из одного базового подграфа, главным образом обусловлен коммуникационными ресурсами вычислительной системы и возможностью построения конвейерной структуры с минимально возможным числом внешних и внутренних информационных каналов. При параллельно–конвейерной организации вычислительного процесса базовый подграф, соответствующий одной ступени конвейера, будет иметь вид, представленный на рис. 5. Каждая ступень конвейера реализует функционально законченный фрагмент P, общее количество которых упорядочено в кортеж (P1 P, ..., P) по числу итераций к. На каждой итерации (k+1) на вход ступени поступает поток операндов, представляющих собой константные значения функции cij на границе области и ее приближения uikj , полученные на предыдущей итерации. Выходом ступени является поток транзитных данных cij и рассчитанных значений uk+1, которые поступают на вход следующей ступени для вычисления узловых значений функции на следующей итерации. Рис. 5. Базовый подграф метода Якоби решения уравнения Лапласа, соответствующий одной ступени вычислительного конвейера Помимо информационных дуг, связанных с поступлением и выдачей вычисляемых приближений функции, структура базового подграфа должна быть дополнена связями, осуществляющими транзит констант ε, γ в следующую ступень конвейера. Также в структуру подграфа вводится дополнительный вход PrIni, на который подается значе- ние предиката предыдущей ступени. Выходной предикат Pri, формируемый внутри подграфа, получается в результате мультиплексирования потока предикатов предыдущих ступеней и собственного вычисленного предиката. Таким образом, в вычислительном конвейере, представленном на рис. 6, достигается параллелизм решения задачи на уровне итераций. Р1 8 р2 8 Y Y ... РП > к+1 / У ^Уу РГ2 ------£—... к+2 / М /у/С^ -----;---^. ... Рис. 6. Параллельно–конвейерная форма метода Якоби решения уравнения Лапласа с применением распараллеливания по итерациям
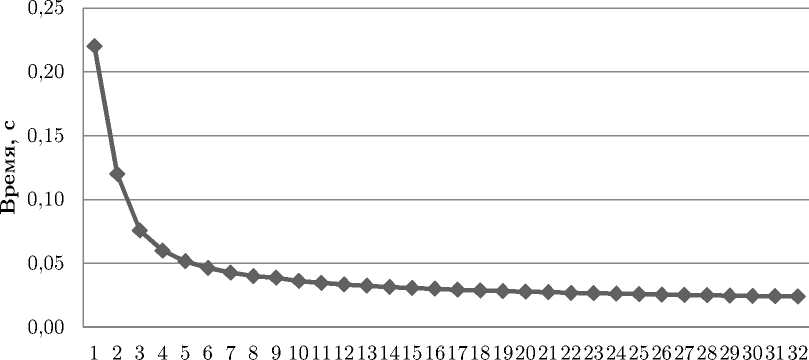
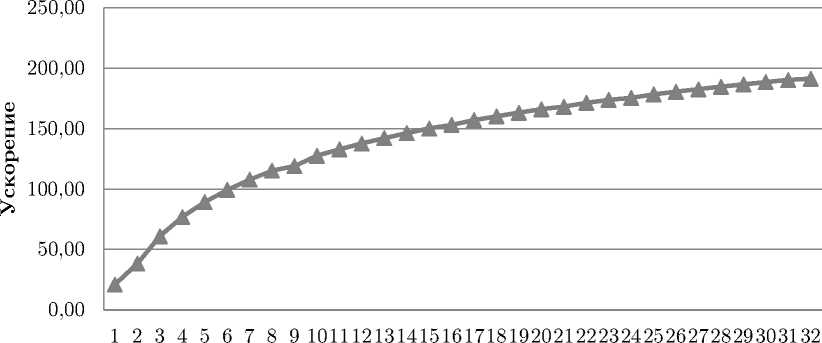
2. Практические результаты решения на РВС краевой задачи Дирихле для уравнения Лапласа Численное решение задачи Дирихле для уравнения Лапласа методом Якоби было реализовано авторами на базовом вычислительном модуле «Тайгета» [16]. В результате аппроксимации 5–точечной разностной схемы на квадратной сетке с шагом h = 0,01 была получена СЛАУ размерностью n = 104. При размещении в одной ПЛИС XC7VX485Т–1FFG1761 (48·106 эквивалентных вентилей, 400 МГц, 192 элементарных процессора стандарта IEEE-754) базового модуля 59 ступеней конвейера время решения СЛАУ составило 0,22 с. Для решения этой задачи на персональном компьютере (Intel Core i5–3570K, 3.4 ГГц, 8 Гб ОЗУ) при использовании одного ядра процессора потребовалось 4,61 с. Таким образом, на одной ПЛИС по сравнению с ПК было получено ускорение вычислений примерно в 21 раз. Всего базовый модуль «Тайгета» содержит 32 ПЛИС, что позволяет разместить в едином решающем поле вычислительный конвейер, состоящий из 1888 ступеней. Масштабирование алгоритма продемонстрировало увеличение скорости решения задачи при увеличении числа используемых кристаллов ПЛИС. На графиках на рис. 7 и 8 представлены полученные экспериментальные результаты для времени решения задачи и ускорения по сравнению с одним ядром процессора Intel Core i5–3570K, 3.4 ГГц для количества ПЛИС от 1 до 32. Результаты вычислительных экспериментов для параллельной реализации на кластере МВС–1000/ИВМ алгоритма численного решения методом Якоби краевой задачи на кластерной многопроцессорной вычислительной системе для числа процессов от 1 до 22 приведены в работе [17]. Согласно полученным в [17] экспериментальным данным, стабильное увеличение ускорения при решении задачи для всех рассматриваемых в [17] вариантов реализации коммуникаций и способа декомпозиции вычислительной области наблюдалось вплоть до использования 22–х процессоров, после чего ускорение решения задачи приобрело неустойчивый характер по причине преобладания времени межпроцессорных обменов над вычислениями. Количество ПЛИС Рис. 7. Метод Якоби решения уравнения Лапласа. Зависимость времени вычислений от числа используемых для решения задачи ПЛИС Количество ПЛИС Рис. 8. Метод Якоби решения уравнения Лапласа. Изменение ускорения в зависимости от числа используемых для решения задачи ПЛИС Согласно данным, приведенным на рис.7 и 8 при использовании ПЛИС для численного решения задачи Дирихле для уравнения Лапласа методом Якоби наблюдается устойчивый рост ускорения решения задачи при увеличении используемого вычислительного ресурса до 32 кристаллов ПЛИС включительно. Параллельно–конвейерная форма реализации матричных задач минимизирует использование внешних выводов, но остается требовательной к остальным вычислительным ресурсам системы – тактовой частоте, объему логики и количеству внутрикристальной памяти ПЛИС. Использование ПЛИС для решения матричных задач позволяет существенно увеличить производительность, в том числе за счет использования кристаллов новых семейств. Так, для каждого следующего семейства ПЛИС Xilinx, начиная с семейства Virtex-4, наблюдается не менее чем 25% рост тактовых частот и, как правило, двукратное увеличение логической емкости ПЛИС. Ресурс встроенной блочной памяти в каждой серии растет еще большими темпами: реализованное на 16 нм техпроцессе семейство Virtex UltraScale+ имеет в четыре раза больше памяти, чем в предыдущей серии Virtex–7 с нормами 28 нм. Поскольку объем внутрикристальной памяти имеет критическое значение для успешной реализации задач решения больших СЛАУ, прогресс этого показателя делает использование ПЛИС весьма перспективным. Заключение Предложенный конвейерно-параллельный способ решения систем линейных уравнений в задачах математической физики может быть применен и к другим итерационным методам, представимым в потоковом виде, среди них: метод Гаусса—Зейделя, попеременно-треугольный метод и так далее. Реализация этого способа сегодня осуществима на ПЛИС и построенных на их основе реконфигурируемых системах, что говорит в пользу широкого использования программируемых архитектур в высокопроизводительных вычислениях. Применение метода распараллеливания по итерациям позволяет существенно сократить количество внешних каналов обмена по сравнению с методами распараллеливания по данным. Поскольку стандартные методы и средства в настоящее время не могут в полной мере решить проблему падения реальной производительности в ряде задач с интенсивным доступом к данным, имеет смысл использовать альтернативные многопроцессорные архитектуры с «гибкой» реализацией различных форм распараллеливания. Среди направлений дальнейших исследований можно выделить поиск эффективных алгоритмов решения на РВС разреженных СЛАУ итерационными методами с различного вида предобуславливанием (на основе неполного LU–разложения, на основе аппроксимации обратной матрицы, на основе алгебраического многосеточного метода и так далее). В настоящее время остается недостаточно изученным вопрос о соотношении времени, затрачиваемого на построение матрицы предобуславливателя, и последующего процесса нахождения решения с сокращенным количеством итераций. Работа выполнена при частичной финансовой поддержке Южного научного центра Российской академии наук по теме№0256-2015-0080 (00–16–15) государственного задания в рамках программы I.5П «Проблемы создания высокопроизводительных, распределенных и облачных систем и технологий. Интеллектуальные информационные технологии и системы».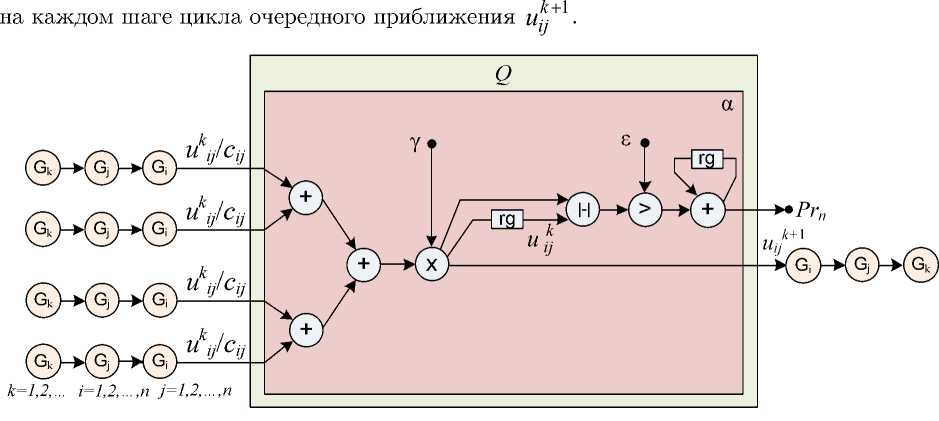
Список литературы Реализация итерационных методов решения систем линейных уравнений в задачах математической физики на реконфигурируемых вычислительных системах
- Самарский А.А., Гулин А.В. Численные методы математической физики: учебное пособие. 2-е изд. М.: Научный мир, 2003. 316 с.
- Гергель В.П. Теория и практика параллельных вычислений. М.: БИНОМ, 2007. 424 с.
- Asanovic K. et al. A view of the parallel computing landscape//Communications of the ACM. 2009. Vol. 52, No. 10. P. 56-67.
- Guo X. et al. Developing a scalable hybrid MPI/OpenMP unstructured finite element model//Computers & Fluids. 2015. Vol. 110. P. 227-234.
- Li R., Saad Y. GPU-accelerated preconditioned iterative linear solvers//The Journal of Supercomputing. 2013. Vol. 63, No. 2. P. 443-466.
- Wolfson-Pou J., Chow E. Reducing Communication in Distributed Asynchronous Iterative Methods//Procedia Computer Science. 2016. Vol. 80. P. 1906-1916.
- Liu X., Zhong Z., Xu K. A hybrid solution method for CFD applications on GPU-accelerated hybrid HPC platforms//Future Generation Computer Systems. 2016. Vol. 56. P. 759-765.
- Deng L. et al. CPU/GPU Computing for AN Implicit Multi-Block Compressible Navier-Stokes Solver on Heterogeneous Platform//International Journal of Modern Physics: Conference Series. World Scientific Publishing Company. 2016. Vol. 42. P. 163-166.
- Stroia I. et al. GPU accelerated geometric multigrid method: Comparison with preconditioned conjugate gradient//High Performance Extreme Computing Conference (HPEC) IEEE. 2015. P. 1-6.
- Каляев И.А. Левин И.И., Семерников Е.А., Шмойлов В.И. Реконфигурируемые мультиконвейерные вычислительные структуры. Ростов-на-Дону: Изд-во ЮНЦ РАН, 2008. 320 с.
- Virtex-6 Family Overview. Xilinx, 2015. URL: http://www.xilinx.com/support/documentation/data_sheets/ds150.pdf (дата обращения: 16.06.2016).
- Series FPGAs Overview. Xilinx, 2015. URL: http://www.xilinx.com/support/documentation/data_sheets/ds180_7Series_Overview.pdf (дата обращения: 16.06.2016).
- UltraScale Architecture and Product Overview. Xilinx, 2016. URL: http://www.xilinx.com/support/documentation/data_sheets/ds890-ultrascale-overview.pdf (дата обращения: 16.06.2016).
- Тихонов А.Н. Самарский А.А. Уравнения математической физики. М.: Наука, 1972. 736 с.
- Левин И.И., Сорокин Д.А., Мельников А.К., Дордопуло А.И. Решение задач с существенно-переменной интенсивностью потоков данных на реконфигурируемых вычислительных системах//Вестник компьютерных и информационных технологий. М.: Машиностроение, 2012. № 2. С. 49-56.
- Левин И.И., Дордопуло А.И., Каляев И.А., Доронченко Ю.И., Раскладкин М.К. Современные и перспективные высокопроизводительные вычислительные системы с реконфигурируемой архитектурой//Вестник ЮУрГУ. Серия «Вычислительная математика и информатика». 2015. Т. 4, № 3. С. 24-39.
- Карепова Е. Д., Шайдуров В. В., Вдовенко М. С. Параллельные реализации метода конечных элементов для краевой задачи для уравнений мелкой воды//Вестник ЮУрГУ. Серия «Математическое моделирование и программирование». 2009. Вып. 3, № 17(150). С. 73-85.


