Реализация многоканальных фильтров в системе остаточных классов

Одной из весьма актуальных задач, стоящих перед современной наукой, является задача создания высокопроизводительных устройств цифровой обработки сигналов. Использование наборов фильтров в значительной степени поспособствовало развитию этого направления. Однако наибольшее распространение в настоящее время получили двухканальные наборы фильтров, что связано прежде всего с бурным развитием разнообразных приложений вейв-лет-анализа [1]. При вейвлетном разложении сигнала используются два канала фильтрации: высокочастотный и низкочастотный. Интерес представляют фильтры с числом каналов большим двух, так как увеличение числа каналов позволяет ускорить обработку сигнала за счет параллельной организации вычислений.

С другой стороны, одним из способов обеспечить максимальную параллельность вычислений при выполнении преобразований сигнала является использование системы остаточных классов (СОК) как альтернативы традиционной позиционной системы счисления (ПСС) [2]. Возможность использования СОК для реализации, например, вейвлетных наборов фильтров была показана в работах

[3-5], были получены хорошие экспериментальные данные.

Целью настоящей статьи является перенос разработанной теории многоканальных фильтров в СОК, чтобы показать возможность совместного использования этих двух перспективных способов увеличения производительности систем ЦОС.

Многоканальные фильтры

Одним из самых распространенных способов цифровой обработки сигнала является фильтрация. В том случае если передаточная функция фильтра, описывающая связь между сигналами на входе и выходе фильтра, задается в виде

N

H^ = b₀ + b_}z~^} + ... + b_Nz”^N = '^b_iz~^l , (1) / = 0

то говорят, что такой фильтр является фильтром с конечной импульсной характеристикой (КИХ-фильтр). Число N называется порядком фильтра. Наиболее широкое распространение получили двухканальные наборы фильтров (см. рис 1, где на рис. 1а изображена прямая форма фильтрации сигнала, а на рис. 1б – многофазная).

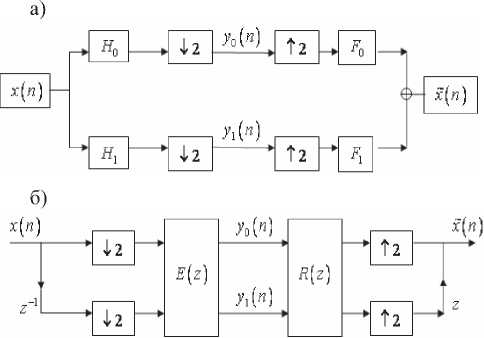
Рис. 1. Двухканальный набор фильтров преобразования сигнала: а) прямая реализация, б) многофазная реализация

Однако в последнее время возрос интерес к многоканальным наборам фильтров [6-7]. Это связано с тем, что увеличение каналов обработки сигнала позволяет увеличить быстродействие системы благодаря большей параллельности вычислений. На рис. 2 изображен M -канальный набор фильтров, рис. 2а представляет его прямую форму, рис. 2б – многофазную. На вход фильтра подается сигнал – последовательность х(/?) , который обрабатывается M анализирующими фильтрами с последующей децимацией. Децимация -I- м означает сохранение для дальнейшей передачи каждого M -го элемента последовательности, остальные M-Y элементы отбрасываются.

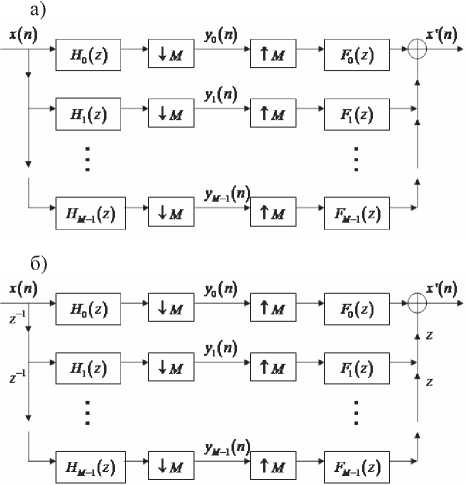
Рис. 2. M -канальный набор фильтров: а) прямая реализация, б) многофазная реализация

Разложение сигнала представляет собой M последовательностей у, (и), 0 <  i < M -1. Для восстановления сигнала используются M синтезирующих фильтров совместно с интерполяцией (прореживанием сигнала). В ходе интерполяции сигнала (на рис. 2 она обозначена T M ) между последовательными элементами входной последовательности вставляются M-Y нулевое значение сигнала. Результатом работы фильтра является выходная последовательность .

Некоторые свойства многоканальных фильтров

Одним из наиболее важных требований к наборам фильтров во многих приложениях цифровой обработки сигналов является возможность получить на выходе фильтра такой же сигнал, который был подан на его вход. Говорят, что фильтр обладает свойством точного восстановления сигнала (perfect reconstruction), если x'(n) = cz Kx^

то есть если сигнал на выходе является композицией сдвига на К шагов и умножения на константу С входного сигнала.

В случае многофазного представления фильтр задается матрицами

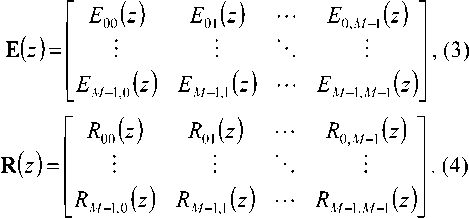
Наиболее распространенным способом добиться свойства точного восстановления сигнала является такое задание матрицы e(z), чтобы она удовлетворяла свойству параунитарности [6], то есть

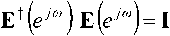
для всех to , где символ t означает сопряженное транспонирование, I – единичная матрица. В этом случае полагают R^^E^e7®), и фильтр, определенный матрицами E(z) и R(z), удовлетворяет свойству точного восстановления сигнала.

Матрицу E(j)

можно представить и в таком виде:

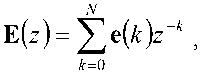
где ®(^) – квадратные MxM матрицы. Тогда если матрица E(z) является параунитарной, то она обладает следующим свойством

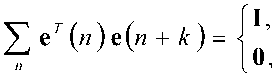
к - 0;

, n (6) к + 0.

Последнее равенство показывает весьма полезное во многих приложениях свойство парау-нитарных фильтров, а именно свойство сохранения энергии сигнала [6].

Связь между прямой и многофазной формами цифрового фильтра определяется по формулам:

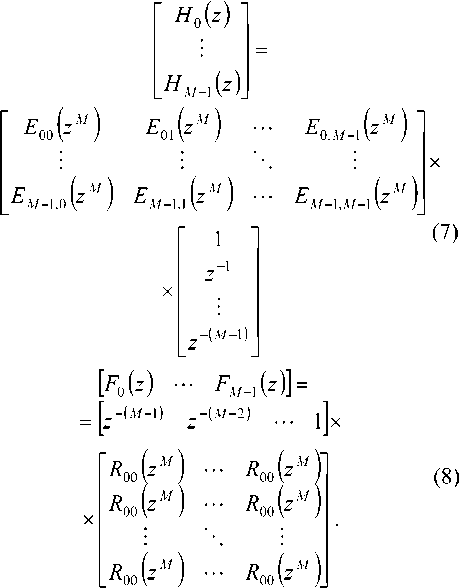
Реализация многоканальных фильтров в СОК

Одним из наиболее перспективных способов увеличения производительности систем цифровой обработки сигналов является использование системы остаточных классов вместо традиционной двоичной арифметики. В СОК числа представляются в базисе взаимно-простых чисел, называемых модулями Р = \тх ...mL}. Любое число X е ZD = ^0;1... D-Ц, где ^ = П,И' и z=i называется диапазоном СОК, имеет единственное представление в СОК ^ ^ {^i  ^3, где

Xj = X mod m.. Как и двоичная арифметика, СОК точна, пока промежуточные вычисления не выходят за пределы диапазона. Взаимно-однозначное соответствие между позиционной системой счисления и СОК устанавливается Китайской теоремой об остатках [2]. Арифметика СОК определяется соответствующими модульными операциями:

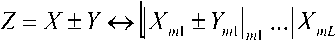
±K4,J’ <9)

Z = Xxy^k ^^l          (10)

где 1^1 означает Q mod m;. . Отдельные модульные операции легко представимы LUT таблицами, расходующими небольшое количество памяти [8]. Основное отличие СОК от традиционных систем счисления заключается в том, что СОК является свободной от переносов, что позволяет производить вычисления с постоянной скоростью для широких диапазонов данных. Это достигается за счет параллельной организации вычислений, существенно сокращающей время обработки данных.

Реализация цифрового фильтра ^(^z)’ определенного по формуле (1), в модулярной арифметике, для отдельно взятого модуля ^mj показана на рис. 3. Для реализации такого фильтра требуются элементы задержки (на рисунке они обозначены символом m ₁ ), а также сумматоры и умножители по модулю m; , обозначенные на схеме соответственно l^l m и I Im . Подробный анализ существующих способов технической реализации модулярных сумматоров и умножителей можно найти в [8]. Полное представление фильтра H(z) в СОК состоит из L каналов по каждому из модулей, где L – общее число модулей в СОК.

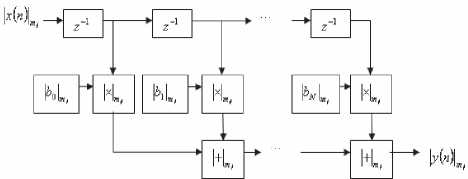
Рис. 3. Прямая реализация фильтра //(r) в СОК, по модулю m j

Для того чтобы реализовать M -канальное разложение сигнала в СОК, необходимо обеспечить параллельную работу фильтров , 0так, как это показано на рис. 2а. При этом для каждого из фильтров H_Z(z) нужно найти его модулярную реализацию по каждому из модулей ^m_A ... m^, и для каждого модуля организовать вычисления так, как это показано на рис. 3. Синтез сигнала посредством фильтров F^z), Q организуется аналогичным образом.

Заключение

Преимущества фильтров с числом каналов большим двух очевидны. За счет параллельной организации вычислений производительность систем из M параллельных каналов обработки сигнала по сравнению с двухканальными возрастет в M/2 раз. Использование СОК позволяет получить дополнительный выигрыш в скорости за счет параллельной модульной организации вычислений по сравнению с традиционными позиционными системами счисления. Совместное использование M-канальных фильтров и СОК от- крывает новые возможности для построения систем цифровой обработки сигналов, значительно превосходящими по своим характеристикам существующие ныне.