Реализация некоторых задач дифференциальной геометрии в программе GeoGebra

Наступает эпоха доминирования в образовании новых информационных технологий как школьной, так и высшей математики.

Рассмотрим некоторые возможности решения математических задач с использованием свободно распространяемой динамической математической программы GeoGebra, которые, на наш взгляд, не нашли еще отражения в имеющихся в распоряжении педагогов учебно-методических материалах.

В практике изучения и преподавания геометрии общего среднего образования наиболее широко распространены такие бесплатно распространяемые интерактивные программы, как The Geometer’s Sketchpad (Живая математика) и GeoGebra. Сравнение этих двух программ показывает, что возможности GeoGebra шире. Например, в отличие от GeoGebra система The Geometer’s Sketchpad не предусматривает построение графика параметрически заданной функции. GeoGebra предлагает более удачное компьютерное сопровождение задач алгебры, начал анализа курса средней школы и начал высшей математики вузовской программы. Немаловажно и то, что эта программа является одной из наиболее широко распространенных, не случайно она переведена на 39 языков.

Мы также сопоставили программу GeoGebra с интерактивной геометрической системой Cinderella, которая используется преимущественно в вузах. Сопоставительный анализ показал, что эти две программы близки по своим возможностям. Однако использование системы Cinderella является более сложным, поскольку доступно лишь для студентов, владеющих навыками программирования.

Из практики использования программного продукта GeoGebra

Программа GeoGebra предназначена прежде всего для решения задач школьного курса геометрии: в ней можно создавать всевозможные чертежи из точек, векторов, отрезков, прямых, строить графики элементарных функ-

ций [1]. К тому же эти конструкции можно динамически изменять варьированием некоторого параметра, входящего в уравнение, а также строить перпендикулярные и параллельные заданной прямой линии, серединные перпендикуляры, биссектрисы углов, касательные, определять длины отрезков, площади многоугольников и др. Все эти возможности позволяют решать любую задачу на построение (с помощью линейки и циркуля) конструктивной геометрии. Кроме того, она также применима во многих других задачах вузовского курса геометрии.

С этой точки зрения рассмотрим некоторые возможности решения некоторых конструктивных задач дифференциальной геометрии в программе GeoGebra. Обратимся к теории кривых, где наиболее часто встречаются задачи на построение эволюты и эвольвенты. Их практическое применение можно найти в теории зубчатых зацеплений.

Рассмотрим сначала прямую задачу.

Пример 1. Построить эволюту. Краткие сведения: если задана кривая y уравнением у: r = r ( t ) такая, что в каждой точке ее кривизна не равна нулю: k ( t ) ≠ 0, то ее эволюта Y определяется уравнением Y: r = ^- ( t ) + p V, где p = 1/ k ( t ) есть радиус кривизны, а V - орт нормали кривой γ в ее точке M ( t ). Используя теорию кривых курса дифференциальной геометрии, можно

• -     ( г’ )² - -„ „

получить, что pv = ( 2 ‘_-‘’ - ) [ k , r ] . Тогда уравнение эволюты в прямоугольной системе координат R = { i, j, k } примет вид:

• -                   fr' )²            -

• Y : r = -(t) —(-Л^[Г, k].

( r ‘ r"k )

Полученное уравнение позволя- ет записать уравнение эволюты как плоской кривой заданной параме- трически:

,  x²² + y²²

x = z — У ----------, y x2y22 - x22y2

, x22 + y22 y=y-x′ x′y′′ - x′′y′

a

Эволюта явно заданной эвольвенты определяется уравнением:

, 1 + y‘²     -■ _f x 1 + y‘²

x = x - y --—y y = y(x)+--— y′′                         y′′

a

Воспользуемся приведенными уравнениями для построения эволюты в системе GeoGebra, например для эллипса, заданного параметрическими уравнениями (рис. 1).

Программа позволяет строить эволюту практически любой кривой: достаточно в представленной реализации изменить уравнение кривой.

Реализация рассматриваемых задач в программе GeoGebra возможна по меньшей мере двумя способами. Первый из них основан на использовании возможности программы построения параметрически заданных функций, а второй основан на применении инструмента «Локус». Заметим, что полученные модели позволяют проводить динамическую интерпретацию кривых: перемещение точки по эволь-

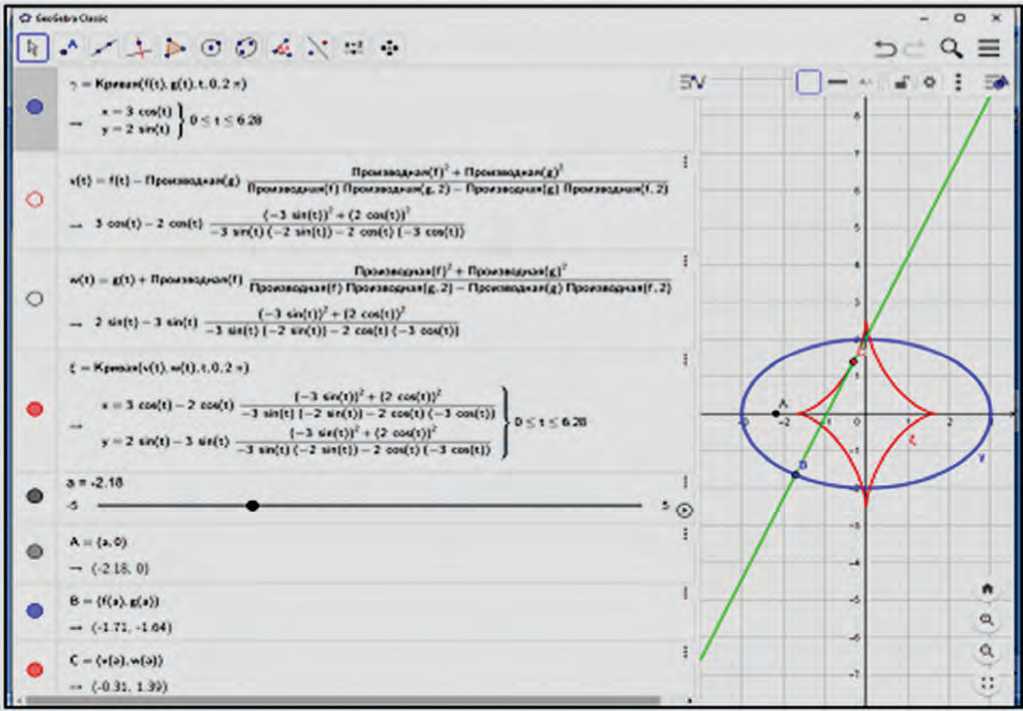
Рис. 1. Динамическая модель эволюты эллипса (составлена авторами)

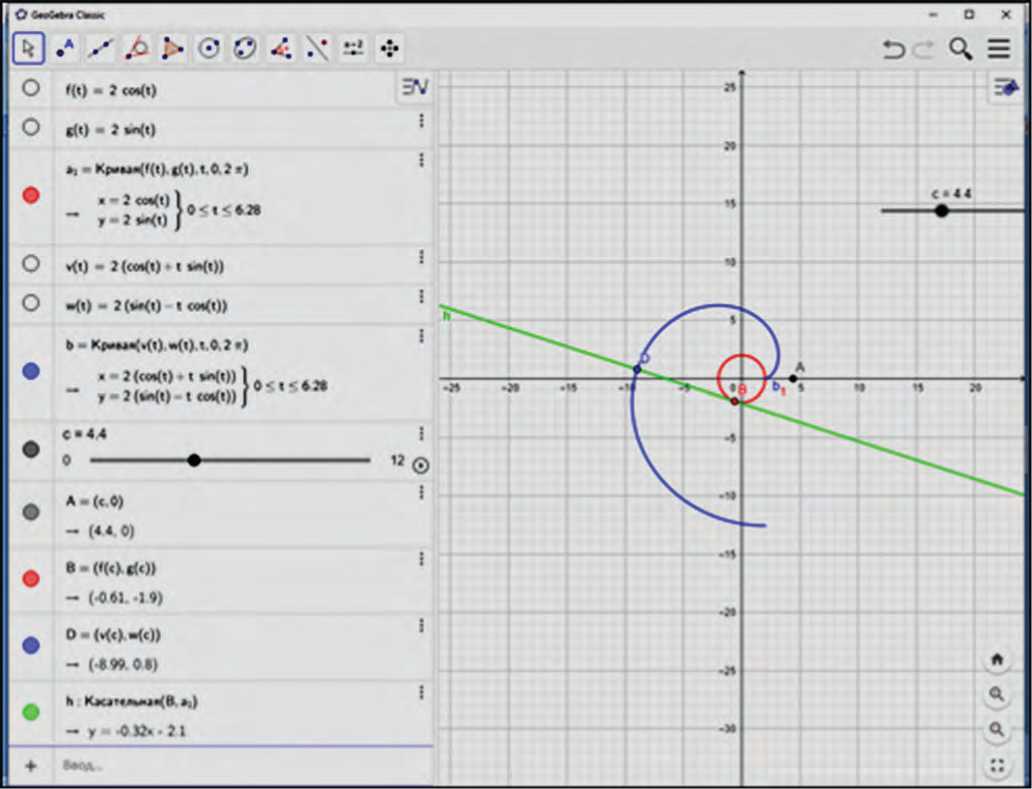
Рис. 2. Динамическая модель эвольвенты окружности (составлена авторами)

венте индуцирует след перемещения точки по эволюте.

Рассмотрим обратную задачу.

Пример 2. Построить эвольвенту. Краткие сведения: эвольвентой кривой у называется кривая γ, для которой данная кривая Y является эволютой. В технических приложениях эвольвенту кривой у понимают как множество концов отрезков касательных кривой у, отложенных от точек касания, длины которых убывают на величину, равную приращению дуги кривой у.

Если кривая задана в естественной параметризации у : Г = У ( s ), то уравнение эвольвенты этой кривой примет вид:

Г( s) = у( s) - (s - s0) у‘( s), или в координатах запишется следующим образом:

x ( s ) = x(s ) + ( s ₀ - s ) x ‘ (s ), y ^{( s} ) = У ^{( s} ) ^{+ ( s} 0 ^{- s} ) y ' ( ^s ).

где s ₀ – произвольная постоянная, определяемая некоторой начальной точкой на у: У = У ( ss ).

Из (4) уравнение эвольвенты для произвольной параметризации запишется в виде:

г                 t

^Г (t ) = У ( t ) - г^-_ f 1^Г'( u)\du.

I ^Г'( t )Г0

Проведем процедуру моделирования эвольвенты (рис. 2) с помощью приведенных уравнений в системе GeoGebra, например окружности:

f ( t ) = 2 cos t , _g ⁽ t ) = ²sin t .

Используя уравнение (6), получаем

v ( t ) = 2(cos t + 1 sin t ), w ( t ) = 2(sin t - 1 cos t ).

Рассмотрим некоторые редко используемые возможности применения системы GeoGebra в школьном курсе математики [6].

Известно, что понятие функции, исследования функций, понятие производной функции традиционно являются одним из наиболее сложных разделов школьной математики. Между тем именно этот раздел имеет принципиальное значение как для самой математики, так и для ее приложений. Поэтому для эффективного усвоения данной тематики обучающимся средней школы необходимо использование наглядных геометрических иллюстраций. Система GeoGebra предоставляет качественные графические возможности для реализации этой идеи. Однако, кроме прямого применения стандартных процедур, имеются и другие,

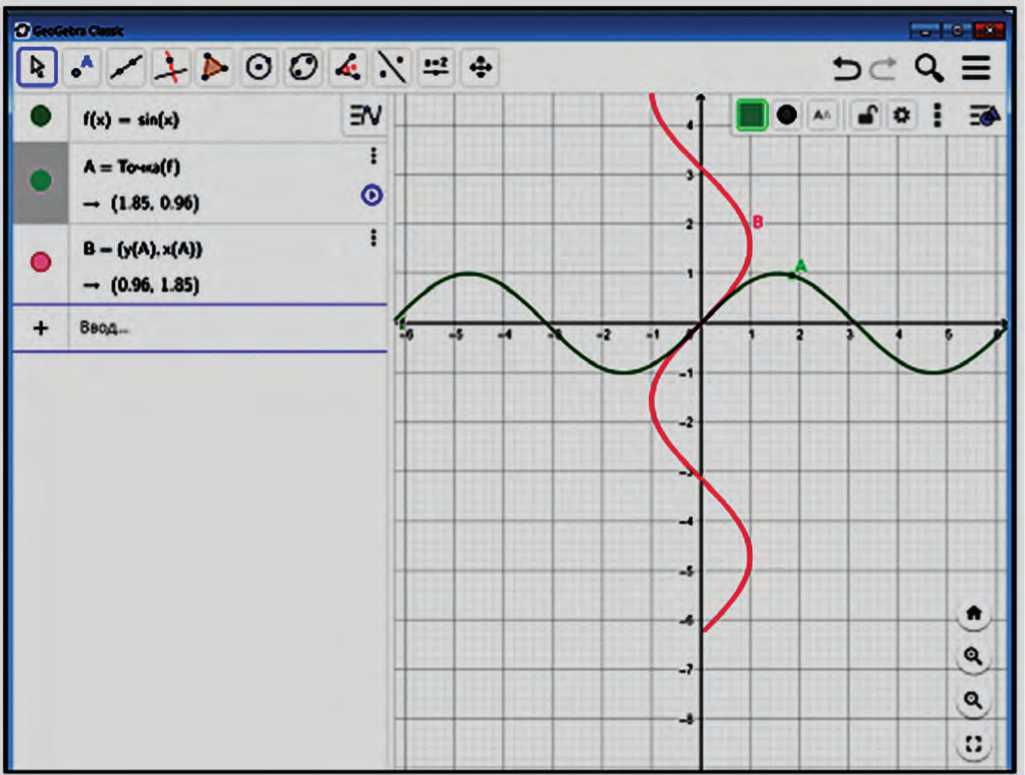
Рис. 3. Построение графика обратной функции в GeoGebra при помощи команды «Локус» (составлено авторами)

мало практикуемые, например применение команды «Локус» (рис. 3). Наглядность различных процедур при решении одной задачи позволяет качественно изучить графические и анимационные модели математических объектов.

Обычно локус в GeoGebra строится так. Сначала активируется инструмент «Локус», затем последовательно реализуются щелчки левой кнопкой мыши сначала по точке A, а затем по зависимой от нее точке B. Точку B можно задавать через строку ввода.

Выводы

Рассматриваемая система GeoGebra является эффективным инструментом компьютерной поддержки изучения математических задач, в частности графической интерпретации ряда основных понятий эволюты и эвольвенты. Предо- ставляемая программой GeoGebra компьютерная поддержка освоения учебно-программного материала по математике позволяет обучающимся прийти к более глубокому пониманию изучаемого раздела математического анализа, конструктивной геометрии или любого другого раздела курса математики, при этом информатика выступает как инструмент формирования учебно-познавательных компетенций.