Реализация оболочки и портала знаний по верификации математических доказательств на платформе IACPAAS

Одной из важнейших задач в математических исследованиях является обеспечение правильности (верификация) доказательств теорем, публикуемых в математической литературе. Одним из перспективных путей решения этой задачи является разработка интерактивных систем поддержки построения доказательств (СППД) [1–3]. Следствием потребности экспериментировать с построением (верификацией) доказательств в рамках разных формальных моделей (специализированных логик) явилась разработка программных оболочек для создания интерактивных СППД (LCF, PVS, Coq, Twelf, HOL Light, Isabelle/HOL и др.) [4–9].

В [10] обсуждалась основная на сегодняшний день причина, по которой СППД, создаваемые с использованием существующих оболочек, остаются мало востребованными в математическом сообществе. Ещё одна причина такого положения дел состоит в том, что большинство таких систем являются однопользовательскими и требуют сложной установки на персональном компьютере. Это требует от математиков достаточной компьютерной грамотности, поэтому предпочтительнее оболочки и прикладные СППД, реализованные и предоставляемые пользователю как облачные сервисы. К настоящему моменту известны две реализации, удовлетворяющие этим требованиям: Isabelle, использующая подсистему Clide [11] и ProofPeer [12]. Но они не имеют расширяемой общей облачной базы знаний, которая могла бы совместно развиваться математическим сообществом, а не только разработчиками этих систем.

Заметим, что для Isabelle существует так называемое централизованное хранилище формальных доказательств ( Archive of Formal Proofs, AFP ). Пользователи могут направлять запросы на добавление формализованных ими теорий (каждая теория представляет собой набор определений, аксиом, теорем/лемм, доказательств) в это хранилище и в случае успешного прохождения процедуры рецензирования эти доказательства становятся частью AFP. Однако данное хранилище не содержит знаний о способах рассуждения, используемых при построении доказательств. Работа с ним строится на тех же принципах, что и работа c распределёнными системами управления версиями, что опять же требует от пользователей высокой компьютерной грамотности. В [12] отмечаются недостатки AFP, связанные со сложностями поиска нужных пользователю теорий, а также проблемами, возникающими при обновлении версий Isabelle. Исследователям нужна база знаний, организованная таким образом, чтобы они могли достаточно легко ориентироваться в ней при поиске необходимой информации.

В [10] представлена концепция программной оболочки для интерактивных систем верификации интуитивных математических доказательств, а также приближенная к математической практике конструирования доказательств формальная система и механизмы её расширения, которые могут быть положены в основу этой оболочки. Настоящая работа посвящена описанию разработки оболочки на облачной платформе IACPaaS [13], тематического портала знаний по верификации интуитивных математических доказательств с использованием средств этой оболочки, а также принципов взаимодействия пользователей с порталом знаний и механизмов его развития.

1 Концептуальная архитектура оболочки для интерактивных систем верификации математических доказательств

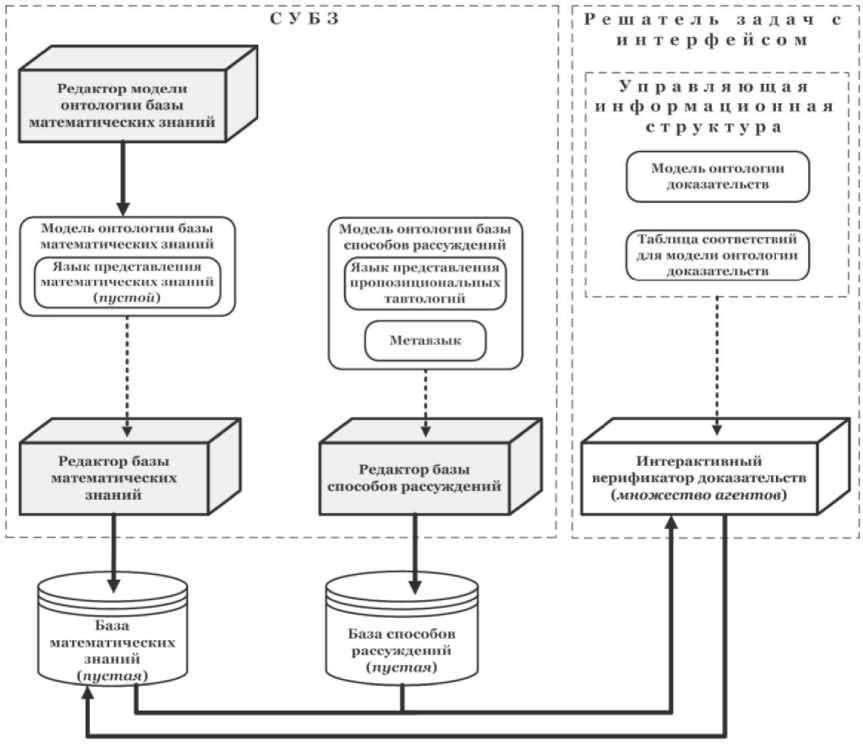
Интерактивные системы верификации интуитивных математических доказательств могут быть отнесены к классу систем, основанных на знаниях (СОЗ), а компоненты описанной в работе [10] оболочки отображены на архитектурные компоненты типичных оболочек СОЗ [14]. В дальнейшем вся терминология работы [10] будет использоваться без ссылок на неё. На рисунке 1 представлена концептуальная архитектура оболочки для интерактивных систем верификации математических доказательств.

В состав оболочки входят: модель онтологии базы математических знаний, включающая пустую спецификацию языка представления математических знаний1; редактор модели онтологии базы математических знаний; модель онтологии базы способов рассуждений, включающая спецификации языка представления пропозициональных тавтологий и метаязыка; редактор базы математических знаний и редактор базы способов рассуждений. Перечисленная совокупность моделей онтологий и редакторов представляет собой систему управления базами знаний (СУБЗ) оболочки. В состав оболочки также входят: модель онтологии доказательств; таблица соответствий для модели онтологии доказательств; мультиагентный интерактивный верификатор доказательств (подробнее см. раздел 3). Данная совокупность компонентов представляет собой решатель задач оболочки, имеющий пользовательский интерфейс. Наконец, оболочка включает в себя пустую базу математических знаний и пустую базу способов рассуждений.

г--------------------1

Решатель задач с i и п т е р ф е й с о м

Модель онтологии базы математических знаний

Г Язык представления ^ математических знаний

I______ (ну стон) ______

У II р а в л я io hi. а я и п <|> о р м а ц и о н п а я структура

База способов рассуждени и (пустая)

С У Б 3

Метаязык

Модель онтологии базы способов рассужден ий пропозициональных тавтологий

Интерактивный верификатор доказательств (множество агентов)

Редактор модели онтологии базы математических знаний

Редактор базы способов рассуждений знании

Редактор базы математических

Модель онтологии доказател ьств для модели онтологии доказательств

Рисунок 1 – Концептуальная архитектура оболочки для интерактивных систем верификации математических доказательств

Редактор модели онтологии базы математических знаний оболочки предназначен для формирования (спецификации) некоторого начального состояния языка представления математических знаний². Редактор базы математических знаний оболочки предназначен для формирования некоторого начального состояния базы математических знаний. Процесс редактирования в нём управляется моделью онтологии базы математических знаний (используемой в качестве метаинформации (метамодели) – на рисунке 1 этот факт демонстрируется пунктирной стрелкой, входящей в соответствующий программный компонент). Редактор базы способов рассуждений оболочки предназначен для формирования начального состояния базы способов рассуждений, процесс редактирования в нём управляется моделью онтологии базы способов рассуждений.

Интерактивный верификатор доказательств реализует итеративный процесс конструирования доказательств в терминах модели онтологии доказательств. Он начинается с задания названия доказательства и выбора (из базы математических знаний) доказываемого утверждения – теоремы, леммы, некоторого следствия. Далее на каждой итерации последовательно выполняются следующие действия.

• 1)    Выбор текущей цели – очередного доказываемого математического утверждения (формулы). В начале доказательства текущей целью является доказываемая теорема (лемма, следствие).

• 2)    Выбор метода доказательства.

• 3)    Выбор способа рассуждения (если метод доказательства не основан на правиле доказательства импликации ( естественного вывода ) ).

• 4)    Выбор значений для посылок при использовании правила Modus ponens (если данное правило было выбрано для вывода или декомпозиции цели ).

Данный процесс заканчивается, когда достигнуто состояние, в котором нет недоказанных целей. Результатом процесса является орграф полного доказательства. Ссылка на этот орграф добавляется в множество ссылок на доказательства утверждения (теоремы, леммы или следствия), принадлежащего базе математических знаний. При этом такая ссылка создаётся не пользователем при формировании базы математических знаний, а интерактивным верификатором доказательств в результате проверки условия завершения процесса конструирования доказательства.

2    Концептуальная архитектура начального состояния портала знаний по верификации математических доказательств

«Пустые» прикладные системы (сервисы) верификации интуитивных математических доказательств, в которых язык представления математических знаний, базу математических знаний и базу способов рассуждений необходимо формировать с нуля, не практичны. Поэтому использование оболочки для создания прикладных сервисов нецелесообразно. В связи с этим возникает потребность в концепте более высокого уровня абстракции (разрабатываемой с использованием средств оболочки), в такой как, например, тематический (специализированный) портал знаний [15] по верификации математических доказательств, который содержал бы некоторое состояние языка представления математических знаний, базы математических знаний и базы способов рассуждений, а также средства их расширения.

На рисунке 2 представлена концептуальная архитектура начального состояния развиваемого портала знаний по верификации математических доказательств. В этом смысле оболочка может рассматриваться как предначальное состояние портала знаний.

В состав начального состояния портала знаний входят: модель онтологии базы математических знаний, включающая спецификацию начального состояния (ядра) языка представления математических знаний; редактор модели онтологии базы математических знаний; редактор базы математических знаний; редактор базы способов рассуждений; решатель задач оболочки. Также в состав начального состояния портала знаний входят начальное состояние базы математических знаний и начальное состояние базы способов рассуждений.

Редактор модели онтологии базы математических знаний (уже как средство портала знаний) предназначен для расширения состояния языка представления математических знаний. Редактор базы математических знаний портала знаний предназначен для расширения состояния базы математических знаний. Процесс редактирования в нём управляется моделью онтологии базы математических знаний. Редактор базы способов рассуждений портала знаний предназначен для расширения состояния базы способов рассуждений. Процесс редактирования в нём управляется соответственно моделью онтологии базы способов рассуждений. Данные редакторы также рассматриваются уже как средства портала знаний.

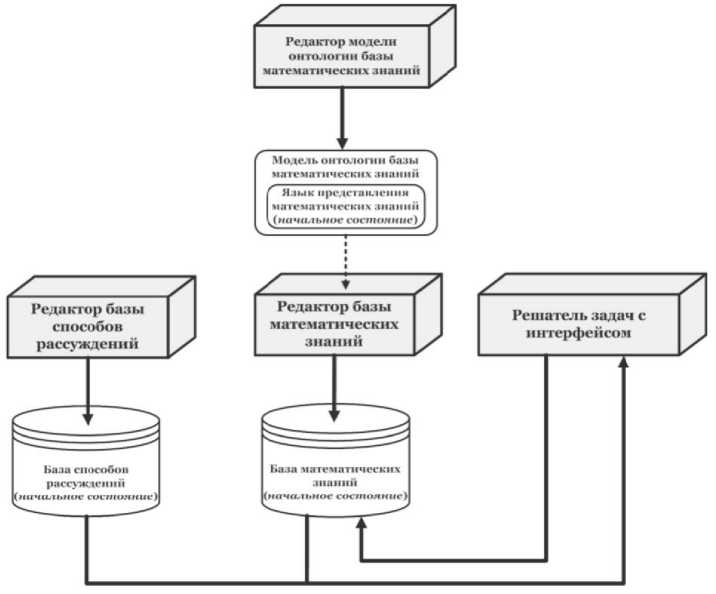
Рисунок 2 – Концептуальная архитектура начального состояния портала знаний по верификации математических доказательств

Все интегрированные в портал ресурсы структурированы в соответствии с их типом и назначением с целью организации удобного поиска и навигации по ним.

3    Разработка оболочки на облачной платформе IACPaaS

Реализация оболочки для интерактивных систем верификации математических доказательств на облачной платформе IACPaaS с использованием предоставляемых ею средств и технологий (инструментария) разработки направлена на обеспечение возможности предоставления оболочки и создаваемого с её использованием начального состояния портала знаний по верификации математических доказательств как облачных сервисов этой платформы (см. рисунок 3).

Разработка всех компонентов СУБЗ оболочки, представленных на рисунке 1, а также пустых базы математических знаний и базы способов рассуждений выполняется с использованием базовой (универсальной) технологии разработки оболочек СОЗ на платформе IACPaaS и инструментальных средств её поддержки. Разработка интерактивного верификатора доказательств и его интерфейса выполняется с использованием специализированной технологии разработки оболочек СОЗ на платформе IACPaaS – на основе информационных структур, управляющих процессом вычисления результата решения задачи (расширенных графовых грамматик) [16].

Использование данной технологии ориентировано на класс задач, для которых явным образом можно специфицировать структуру результата их решения в форме связного орграфа – орграфа грамматики (метаинформации, модели), а процесс вычисления самого результата, который также представляет собой связный орграф (орграф информации, компонента), организовать в виде его пошагового формирования «сверху-вниз».

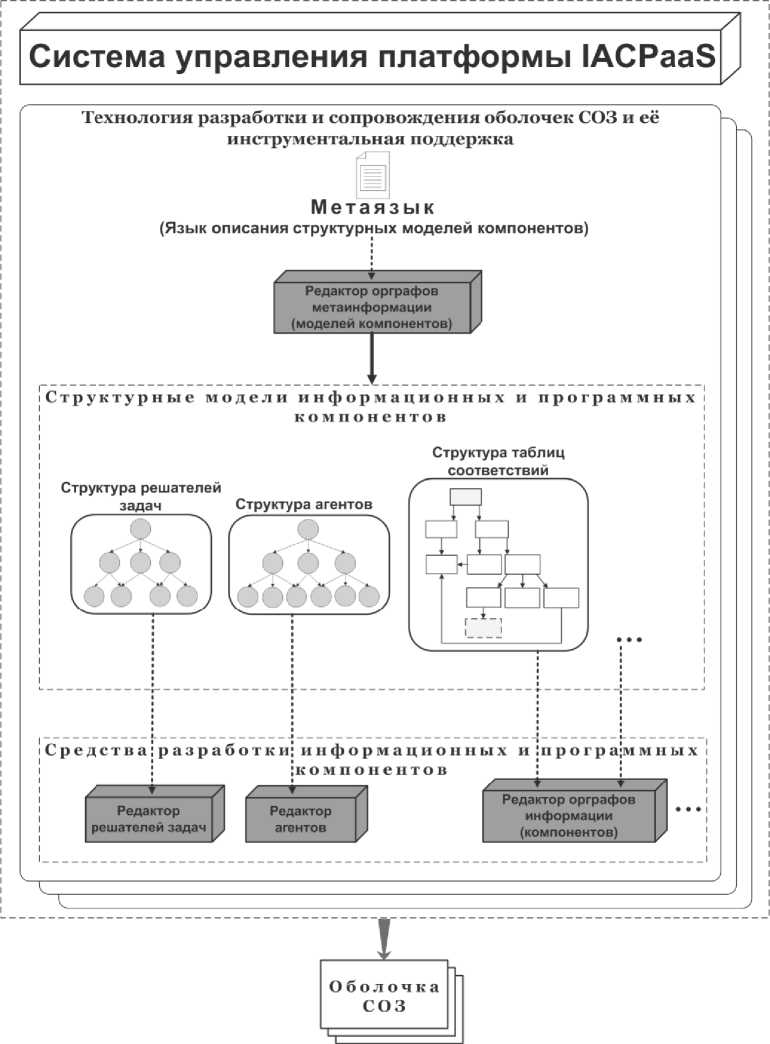
Рисунок 3 – Инструментарий для разработки оболочек СОЗ на облачной платформе IACPaaS

В основу технологии положено явное описание орграфа информационной структуры, управляющей процессом решения задачи (либо нескольких таких взаимосвязанных орграфов). Расширение графовой грамматики представляет собой орграф специального вида, называемый таблицей соответствий. Она сопоставляет вершинам орграфа грамматики программные модули (агенты), которые формируют результат решения задачи, предоставляя, возможно, для этого необходимый пользовательский интерфейс. Обращения к агентам осуществляет обеспечивающий инструментальную поддержку данной технологии интерпретатор орграфов управляющих структур. Он обеспечивает взаимодействие пользователя (пользовательский интерфейс) с управляющей структурой и является ядром решателей задач оболочек, разрабатываемых по данной технологии. При этом предоставляемый пользовательский интерфейс интерпретатора может расширяться интерфейсными возможностями, которые реализуют агенты, указанные в таблице соответствий.

В случае с разработкой интерактивного верификатора доказательств орграфом управляющей структуры является орграф грамматики, представляющий модель онтологии полных доказательств. Он связан с орграфами, представляющими модель онтологии базы математических знаний и модель онтологии базы способов рассуждений. Посредством таблицы соответствий некоторым вершинам орграфа модели онтологии полных доказательств сопоставляются обращения к агентам, которые реализуют семантику методов доказательств целей, а также алгоритмы однонаправленной унификации (сопоставления) и применения подстановки. В процессе работы эти агенты формируют фрагменты орграфа доказательства в соответствии с синтаксической структурой методов доказательств (описанных в модели онтологии доказательств).

Разработка каждого информационного и программного компонента оболочки подразумевает: 1) создание с использованием Системы управления на web-сайте облачной платформы IACPaaS в соответствующем разделе личного кабинета разработчика оболочки новой представляющей этот компонент единицы хранения (орграфа грамматики или орграфа информации) нужного типа (« метаинформация », « информация », « агент », « решатель ») с пустым содержимым (орграф представлен единственной корневой вершиной)³; 2) формирование содержимого созданной единицы хранения «сверху-вниз» (начиная с корневой вершины орграфа) с использованием соответствующего инструментального средства платформы.

• 3.1    Разработка компонентов системы управления базами знаний

Функциональность и интерфейс редактора « Редактор модели онтологии базы математических знаний » полностью реализуется инструментальным средством платформы IACPaaS « Редактор орграфов метаинформации ». Модель процесса редактирования, положенная в основу данного редактора, построена на семантике конструкций декларативного метаязыка , используемых для спецификации орграфов грамматики (метаинформации). Метаязык, используемый здесь как средство спецификации формальных систем, состоит из трёх подъязыков: языка описания порождающих графовых грамматик, языка описания контекстных условий и языка описания порождающих текстовых грамматик, описанных в [10, 17].

Разработка орграфа грамматики, представляющего модель онтологии базы математических знаний , включающей описание пустого языка представления математических знаний, состоит в создании в разделе « Онтологии » личного кабинета разработчика оболочки новой единицы хранения типа « метаинформация » и формировании её содержимого с использованием редактора « Редактор орграфов метаинформации » как показано на рисунке 4.

Аналогично выполняется разработка орграфа грамматики, представляющего модель онтологии базы способов рассуждений, включающей описание языка представления пропозициональных тавтологий и метаязыка (языка представления метаматематических утверждений): их абстрактного и конкретного синтаксиса, а также контекстных условий для этих языков (рисунок 5).

Рисунок 4 – Структура базы математических знаний и математического утверждения в интерфейсе инструментального средства платформы « Редактор орграфов метаинформации »

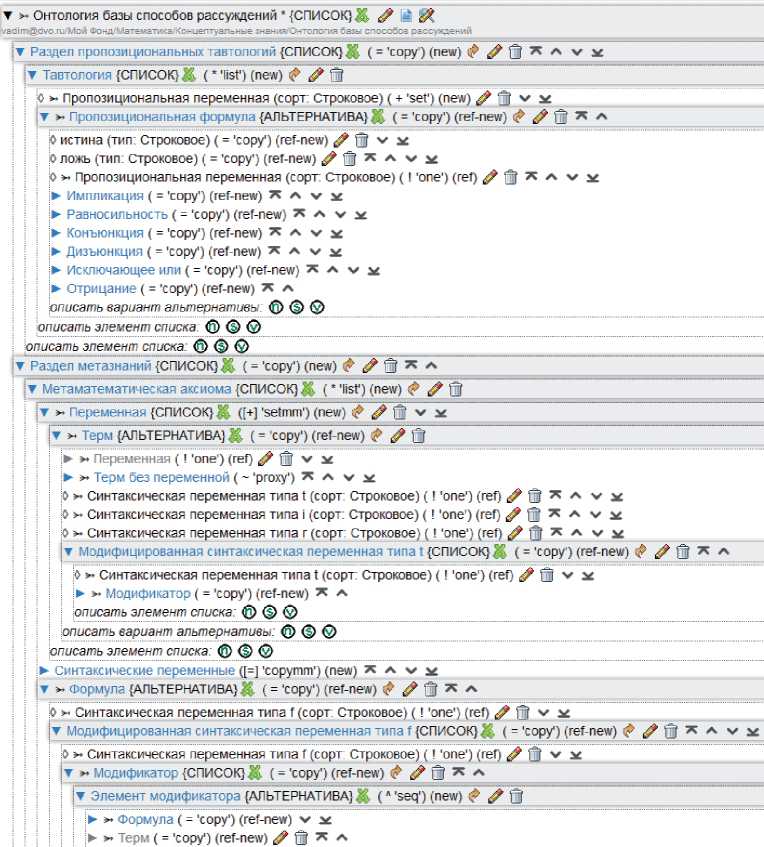
Рисунок 5 – Модель онтологии базы способов рассуждений в интерфейсе инструментального средства платформы « Редактор орграфов метаинформации »

« Редактор базы математических знаний » создаётся путём подключения к инструментальному средству платформы IACPaaS « Редактор орграфов информации » модели онтологии базы математических знаний в качестве информации, управляющей генерацией пользовательского интерфейса и процессом формирования базы математических знаний с проверкой её полноты и заданных в модели онтологии контекстных условий. Аналогично, « Редактор базы способов рассуждений » создаётся путём подключения к средству « Редактор орграфов информации » модели онтологии базы способов рассуждений.

• 3.2    Разработка интерактивного верификатора доказательств

• 3.2.1    Разработка модели онтологии доказательств

• 3.2.2    Разработка таблицы соответствий для модели онтологии доказательств

Разработка интерактивного верификатора доказательств с интерфейсом включает создание: орграфа грамматики, представляющего модель онтологии полных доказательств; таблицы соответствий для него; решателя задач – множества агентов, обращения к которым выполняются (непосредственно или опосредованно) интерпретатором орграфов управляющих структур через таблицу соответствий; декларативной спецификации решателя задач, описывающей его связь с формальными параметрами4, таблицей соответствий, базой математических знаний и базой способов рассуждений, а также пользовательским интерфейсом.

Разработка орграфа грамматики, представляющего модель онтологии доказательств , состоит в создании в разделе « Онтологии » личного кабинета разработчика оболочки новой единицы хранения типа « метаинформация » и формировании её содержимого с использованием инструментального средства платформы « Редактор орграфов метаинформации » (рисунок 6).

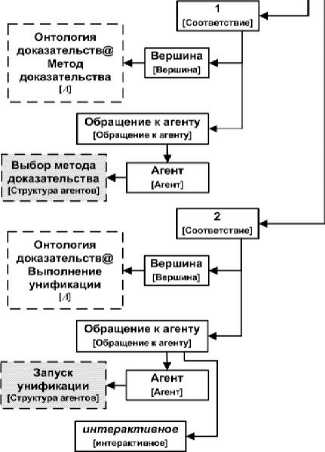
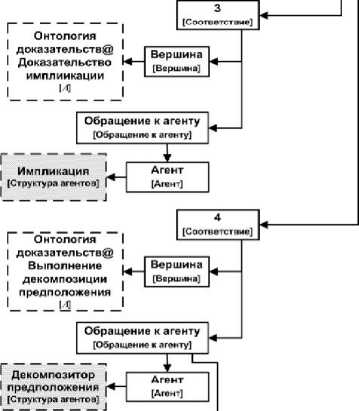
Разработка орграфа информации, представляющего таблицу соответствий, состоит в создании в разделе «Решатели» новой единицы хранения типа «информация»5 и формировании её содержимого с использованием инструментального средства платформы «Редактор орграфов информации». Орграф грамматики «Структура таблиц соответствий» подключён к данному редактору в качестве информации, управляющей процессом формирования таблиц соответствий. На рисунке 7 показана таблица соответствий между понятиями модели онтологии доказательств и агентами решателя задач оболочки, представленная в форме орграфа.

Для каждого обращения к агенту вершина «интерактивное» представляет собой логический признак. Он определяет, как в процессе формирования орграфа информации (орграфа доказательства) это обращение должно выполняться: автоматически или по инициативе пользователя. Корневая вершина орграфа закрашена серым цветом. Вершины, изображенные пунктирными прямоугольниками, принадлежат орграфам, отличным от данного орграфа, т.е. представляющим другую метаинформацию или информацию. На рисунке 7 таковыми являются вершины, принадлежащие орграфу метаинформации, представляющему модель онтологии доказательств, а также корневые вершины орграфов информации, описывающих декларативные спецификации агентов решателя задач. Символ «@» в метках вершин, представленных пунктирными прямоугольниками, разделяет метку корневой вершины стороннего орграфа и метку той его вершины (не совпадающей с первой), которая является корневой вершиной повторно используемого подграфа. В квадратных скобках у вершин указаны метки соответствующих им вершин из орграфа грамматики (метаинформации).

• ▼ »• Онтология доказательств' {СПИСОК} X ^ В ^

vadim@dvo ru/Мой Фонд/Математика/Концептуальные знания/Онтология доказательств

Д Доказательство 2 {СПИСОК} X (* list') (new) ^ ^ Q

|т Теорема * {СПИСОК} X (= ’copy") (new) ^ ^ Д

—• Предложение (! ' one') (ref) ______________________________________________

; ▼ » Метод доказательства * {АЛЬТЕРНАТИВА} X ( ='copy') (new) ^ ^ Д Ж л v ^

► Не импликация без предположений (= 'copy') (new) v ж

► Импликация без предположений (= 'copy') (new) ^ л v ^

► Не импликация ^предположениями (= 'copy') (new) ж л v ^

▼ Импликация с предположениями {АЛЬТЕРНАТИВА} X ( ⁼ 'copy') (new) (? ^ Q ^ ^

> » Унификация * ( = 'copy') (new) v at_____                          _______________

;   ; т >• Декомпозиция цели * {СПИСОК} X (- 'copy') (new) ^ ^ 9 * a v ^

> » Справедливое утверждение * (= 'copy') (new) v ^

> >• Выполнение декомпозиции цели * (= 'copy') (new) тс л описать элемент списка: © © © ф ©

▼ * Вывод * {СПИСОК} X ( = 'copy') (new) ^ ^ Д Ж л V ^ ]▼ Шаг вывода {СПИСОК} X (“'seq') (new) ^ ^ Д v х

;   ;   ; ► х Справедливое утверждение * ( = 'copy') (new) v ^__ i ▼ » Формирование посылок {АЛЬТЕРНАТИВА} X ( = 'copy') (new) ф ^ Д ж л v ж

;   ;   ;   ; ► Инвертировать способ рассуждения * ( = 'copy') (new) V ^______

;   ;   ;   ^ ▼ »• Посылки {СПИСОК} X (~ 'proxy') £ ^ Д Ж Л

▼ Посылка {СПИСОК} X ( * 'seq') (new) ф ^ Q V ^

i i i i > >• Формулировка посылки *( = 'copy') (new) v ^ ;;;;;► Значение посылки * (= 'copy') (new) ^ л i i i i i описать элемент списка: © © © ф ©

► >- Формирование результата шага вывода * ( = 'copy') (new) х л описать элемент списка ® ® © ф © описать вариант альтернативы © ® © ф ©

► Результаты шага вывода * (= 'copy') (new) ^ л описать элемент списка: © © © ф ©

> Результаты выполненных шагов вывода * (= 'copy') (new) ^ л Описать элемент списка: © ® © ф ©

▼ »• Декомпозиция предположения‘{СПИСОК}X ( ='copy') (new) t^ ^ Д X zs v ^

; > Предположение * (= 'copy') (new) v м

> » Справедливое утверждение * (= 'copy') (new) Ж л v ^

> » Выполнение декомпозиции предположения * (= 'copy') (ref-new) ^ л Описать элемент списка: © © © ф ©

► » Доказательство импликации * (= 'copy') (new) ^ л

Описать вариант альтернативы: © © © ф ©

Описать вариант альтернативы: © © © ф ©

► Вспомогательные утверждения * ([=] 'copymm') (new) ^ *

Рисунок 6 – Модель онтологии доказательств в интерфейсе инструментального средства платформы « Редактор орграфов метаинформации »

• 3.2.3    Разработка агентов решателя задач

В данном разделе описывается обобщённый процесс разработки агентов, указанных на рисунке 7. Обращения к этим агентам выполняются при создании вершин в орграфе доказательства, соответствующих вершинам из орграфа грамматики, представляющего модель онтологии полных доказательств, также указанных на рисунке 7. Шаблоны сообщений, посредством которых интерпретатор орграфов управляющих структур взаимодействует с описанными в орграфе агентами, доступны в Фонде платформы IACPaaS для использования.

Таблица соответствий для орграфа грамматики модели онтологии доказательств [Структура таблиц соответствий]

Г Онтология ।

| доказательств И—

Орграф метаинформации [Орграф метаинформации!

интерактивное [интерактивное]

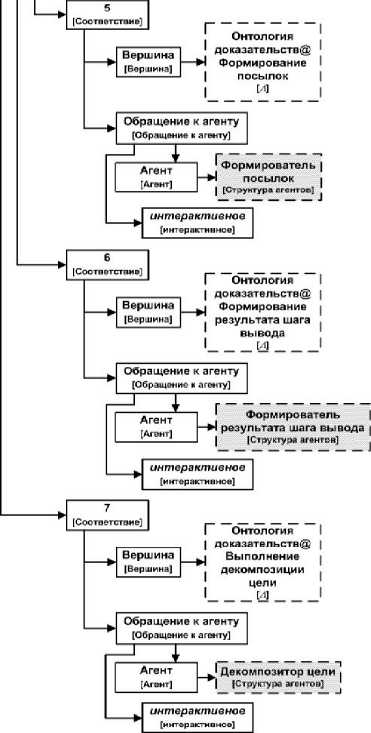
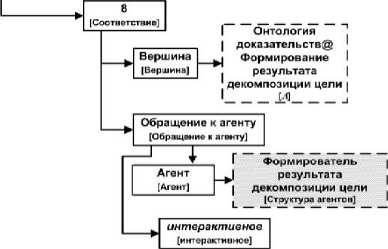
Рисунок 7 – Орграф таблицы соответствий между понятиями модели онтологии доказательств и агентами решателя задач оболочки

Разработка агента состоит в формировании в разделе « Агенты » единицы хранения -орграфа информации, представляющего декларативную спецификацию агента⁶; генерации заготовки исходного кода агента по его декларативной спецификации; написании исходного кода агента, реализующего его семантику (с использованием предоставляемого платформой API); получении байт-кода агента (в результате компиляции исходного кода) и загрузки его в Фонд – в соответствующую единицу хранения.

Агент « Выбор метода доказательства » предоставляет множество альтернативных вариантов для выбора метода доказательства текущей цели в зависимости от синтаксической формы её утверждения (имеет ли оно форму импликации или нет) и наличия или отсутствия у неё предположений.

Если утверждение имеет вид импликации и список предположений не пуст, то Метод доказательства ∈ {“Унификация”, “Декомпозиция цели”, “Вывод”, “Декомпозиция предположения”, “Доказательство импликации”}. Если утверждение не является импликацией и список предположений не пуст, то Метод доказательства ∈ {“Унификация”, “Декомпозиция цели”, “Вывод”, “Декомпозиция предположения”}. Если утверждение имеет вид импликации и список предположений пуст, то Метод доказательства ∈ {“Унификация”, “Декомпозиция цели”, “Вывод”, “Доказательство импликации”}. Если утверждение не является импликацией и список предположений пуст, то Метод доказательства ∈ {“Унификация”, “Декомпозиция цели”, “Вывод”}.

Агент « Запуск унификации » подготавливает входные данные для агента, реализующего алгоритм унификации (точнее, её так называемый однонаправленный вариант – сопоставление [18]) – справедливое утверждение, выбранное пользователем из базы математических знаний или базы способов рассуждений, и частное утверждение – доказываемую цель. Принимает от агента, реализующего алгоритм унификации, результат, и если унификация не выполнена, то отображает пользователю соответствующее сообщение; если унификация выполнена, то формирует множество новых целей (если в процессе унификации появились вспомогательные утверждения).

Агент « Импликация » реализует правило доказательства импликации (естественного вывода).

Агент « Декомпозитор предположения » реализует семантику применения правила Modus ponens (правило отделения) для декомпозиции предварительно выбранного пользователем предположения из списка предположений доказываемой цели; если в процессе удачно выполненной унификации появились вспомогательные утверждения, то формирует множество соответствующих новых целей.

Агенты « Формирователь посылок » и « Формирователь результата шага вывода » реализуют семантику применения правила Modus ponens для выполнения шагов вывода. Агент «Формирователь посылок» организует выбор пользователем справедливого утверждения в форме импликации или равносильности. При этом если выбранное утверждение имеет форму равносильности, то пользователю задаётся вопрос о необходимости инвертирования данной равносильности. Если равносильность необходимо инвертировать, то правая часть равносильности считается условием, а левая – заключением. По количеству конъюнктов в условии импликации (или части равносильности, считающейся условием) агент формирует множество посылок. Формулировка каждой посылки есть формулировка соответствующего конъюнкта. Значение посылки в зависимости от наличия предположений у доказываемой цели и уже выполненных шагов вывода может быть выбрано пользователем из условий:

• ■    если у доказываемой цели есть предположения и выполнен хотя бы один шаг вывода -базы математических знаний, списка предположений цели, результатов выполненных шагов вывода;

• ■    если у доказываемой цели есть предположения, но еще не выполнено ни одного шага вывода – базы математических знаний, списка предположений цели;

• ■    если у доказываемой цели отсутствуют предположения и выполнен хотя бы один шаг вывода – базы математических знаний, результатов выполненных шагов вывода;

• ■    если у доказываемой цели отсутствуют предположения и еще не выполнено ни одного шага вывода – базы математических знаний.

• 3.2.4 Разработка декларативной спецификации решателя задач интерактивного верификатора доказательств

Агент « Формирователь результата шага вывода » даёт задание на унификацию (агенту, реализующему данный алгоритм) условия справедливого утверждения с формулой, представляющей собой конъюнкцию выбранных значений посылок. Если унификация выполнена, то формирует результат шага вывода, представляющий собой результат подстановки унификатора в заключение справедливого утверждения, а также множество новых целей (если в процессе унификации появились вспомогательные утверждения). В противном случае отображает пользователю сообщение о невозможности унификации формул. После формирования результата очередного шага проверяется условие окончания процесса вывода.

Агенты « Декомпозитор цели » и « Формирователь результата декомпозиции цели » реализуют семантику применения правила Modus ponens для выполнения декомпозиции цели. Выполняется унификация доказываемой цели и заключения импликации (или части равносильности) выбранного пользователем справедливого утверждения из базы математических знаний или базы способов рассуждений. При этом если последнее имеет форму равносильности, в которой одна из её частей имеет форму конъюнкции, а другая не имеет, то частью равносильности, участвующей в унификации – заключением равносильности, является часть, не имеющая формы конъюнкции. Если унификация не выполнена, то, если справедливое утверждение имеет форму импликации, пользователю отображается сообщение о невозможности унификации формул, а если справедливое утверждение имеет форму равносильности, то даётся задание на унификацию доказываемой цели и другой части равносильности. Если унификация выполнена, то формируется множество новых целей (если в процессе унификации появились вспомогательные утверждения), в противном случае пользователю отображается сообщение о невозможности унификации формул.

Выполняется подстановка (агентом, реализующим алгоритм подстановки) вычисленного унификатора во все конъюнкты условия импликации (или части равносильности, не участвовавшей в последней унификации). Результат подстановки есть множество новых целей, количество которых равно количеству конъюнктов. Список предположений каждой новой цели совпадает со списком предположений доказываемой цели.

Разработка в разделе « Решатели » орграфа информации, представляющего декларативную спецификацию решателя задач интерактивного верификатора доказательств, состоит в создании новой единицы хранения типа « решатель » и формировании её содержимого с использованием инструментального средства платформы « Редактор решателей задач ».

Корневой агент решателя задаётся путём создания ссылки на корневую вершину орграфа информации в Фонде платформы IACPaaS, представляющего декларативную спецификацию агента « Универсальный корневой агент редакторов и просмотрщиков ». Агент Интерфейсный контроллер решателя задаётся путём создания ссылки на корневую вершину орграфа информации в Фонде платформы IACPaaS, представляющего декларативную спецификацию агента « Интерфейсный контроллер расширяемых редакторов и просмотрщиков единиц хранения » (рисунок 8). Данный агент реализует функциональные возможности интерпретатора орграфов управляющих структур.

В качестве выходного формального параметра указывается (путём создания ссылки на его корневую вершину) орграф грамматики, представляющий модель онтологии доказательств. Выходными фактическими параметрами , указываемыми при создании прикладных сервисов с использованием оболочки, являются орграфы информации, представляющие формируемые по модели онтологии доказательств базы доказательств.

Среди собственных информационных ресурсов необходимо указать орграфы информации, представляющие соответственно таблицу соответствий для орграфа грамматики модели онтологии доказательств , базу математических знаний и базу способов рассуждений .

Связывание пользовательского интерфейса с решателем задач состоит в создании web-страницы с названием « Интерактивный верификатор доказательств » и содержимым, показанным на рисунке 8. Необходимые интерфейсные элементы создаются с использованием предоставляемого платформой API при написании исходного кода агентов, реализующих соответствующую семантику.

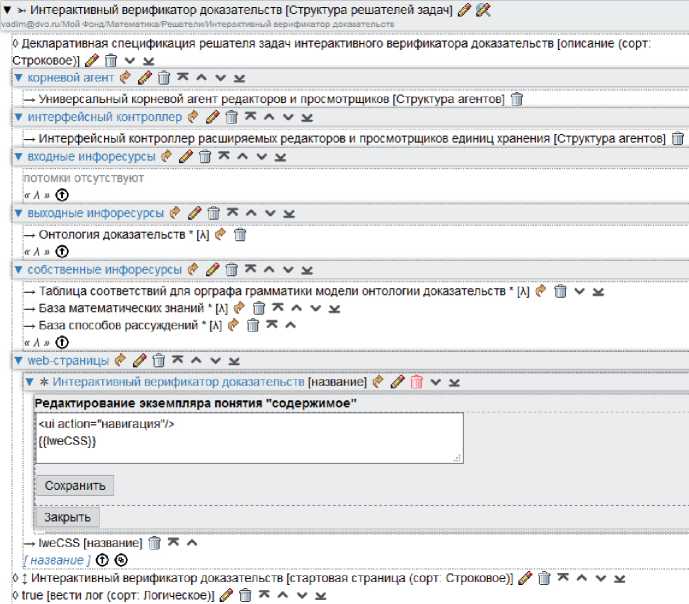
Рисунок 8 – Декларативная спецификация решателя задач интерактивного верификатора доказательств в интерфейсе инструментального средства « Редактор решателей задач »

• 3.3 Разработка пустых базы математических знаний и базы способов рассуждений

Разработка орграфа информации, представляющего базу математических знаний, состоит в создании в разделе « Базы знаний » новой единицы хранения типа «информация». В качестве метаинформации при этом указывается хранящийся в разделе « Онтологии » орграф грамматики « Онтология базы математических знаний ». Аналогично, разработка орграфа информации, представляющего базу способов рассуждений, состоит в создании в разделе «Базы знаний» новой единицы хранения типа «информация» с указанием в качестве метаинформации орграфа грамматики « Онтология базы способов рассуждений ».

4 Разработка начального состояния портала знанийс использованием оболочки

Разработка начального состояния портала знаний по верификации математических доказательств выполняется с использованием средств, входящих в состав оболочки, а также Си- стемы управления облачной платформы IACPaaS. Структура портала знаний по верификации математических доказательств формируется с помощью Системы управления на web-сайте облачной платформы IACPaaS в личном кабинете разработчика портала. Структура представляет собой дерево разделов, терминальными вершинами которого являются информационные и/или программные компоненты (ресурсы) портала, отнесённые к определённому разделу по некоторому отличительному признаку: типу, целевому назначению и т.п. Также с помощью Системы управления начальное состояние портала знаний переносится в Фонд платформы, где он становится общедоступным, и назначается ответственный за данный портал администратор, который контролирует его дальнейшее развитие.

Разработка начального состояния ( ядра ) языка представления математических знаний состоит в расширении орграфа грамматики, представляющего модель онтологии базы математических знаний, конкретными типами формул и термов с использованием редактора оболочки « Редактор модели онтологии базы математических знаний » (рисунок 9).

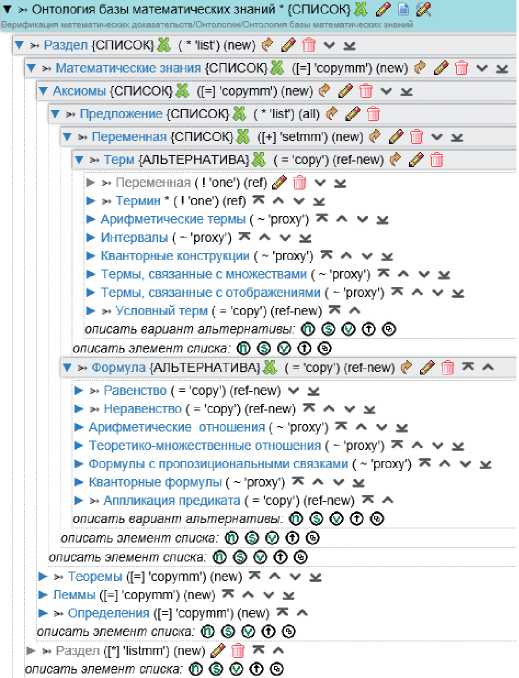
Рисунок 9 – Начальное состояние языка представления математических знаний в интерфейсе средства портала « Редактор модели онтологии базы математических знаний »

Разработка начального состояния ( ядра ) базы математических знаний состоит в формировании содержимого представляющего её орграфа информации с использованием редактора оболочки « Редактор базы математических знаний » (рисунок 10). Разработка начального состояния ( ядра ) базы способов рассуждений состоит в формировании содержимого представляющего её орграфа информации с использованием редактора оболочки « Редактор базы способов рассуждений » (рисунок 11).

Начальное состояние базы математических знаний содержит раздел «Арифметика», который содержит 29 аксиом, 17 теорем, 3 определения и 4 леммы. Начальное состояние базы формализованных способов рассуждений содержит 29 способов рассуждений: 5

пропозициональных тавтологий и 24 метаматематических утверждения.

• ▼    ** База математических знаний * [Онтология базы математических знаний] ^ й ® ^ vadim@dvc.ru/Mofl Фонд'Математика^|,Математниеск№ знания''База математических знаний

!▼ Арифметика [Раздел] @ v х

• ▼    Ма ема 1ические знания ^ ^ 3 ^v ^

• ►    Аксиомы V- х

• ▼    Юоремы (^ ^ 3 ^ ^{А v} ^

• ►    >• lp-.нзитивность отношения "меныпе" [I редложение] v х

• ►    >• Разность одинаковых значений [Предложение] ж a v х

• ►    »• Почлешюе сложение itepaueiK i и [Предложение) Ж a v х

• ►    »• Дис!рибу1ИВ1ЮС!ь иычи1ания и умножения [Предложение] ж a v х

• ►    >• Умножение на нуль [Предложение] ж a v х

• ►    г очпенное перемножение неразенств [Предложение; ж a v х

• ►    »• Произведение положительных чисел положительно Предложение] ж a v х

• ►    »• Произведение положительного и отрицательного чисел отрицательно [Предложение] Ж a v х

• ►    Произведение двух отрицательных чисел положительно [Предложение" Ж a v х

• ►    ** Связь отношения "больше" и разности [Предложение Ж a v х

• ►    ** Бели произведение О, то один из сомножителей О [ 1редпожение] ж a v х

• ►    »• Почленное произведение нсраос!ктв с положительными членами [I !рсдложснис] ж a v х

• ►    Если моду! ь разносiи не превосходиi некоюрою числа, ю модуль уменьшаемою не превосходи! суммы модуля

иычи1аемою и aim о числа [Предложение] ж a v х

• ►    *- Ecj и мзду! ь а - b меньше с, ю а больше b - с [Пред! ожение] ж a v х

• ►    >• Множество отрицательных чисел есть подмножество множества вещественнь х чисел (Гредложение] ж a v х

• ►    Следствия ж a v х

• ►    »• Пели а не равно Р, то оно или больше или меньше b [Предложение] Ж а

• f Предложение j ©

• ►    Определения ж a v х ► Леммы ж а

• Рисунок 10 – Начальное состояние базы математических знаний в интерфейсе средства портала «Редактор базы математических знаний»

• ▼    Раздел пропозициональных тавтологий ^ ^ £* ж a v х

• ►    >• Декомпозиция равносильности [Тавтология] v х

• ►    *• 1ранзитивность равносильности 11лвтогогия| ж a v х

• ►    >• Доказаюльс iuooi прЭ1ивною flauioi Э1ия] Ж a v х

►/.оказательство противоречия [ 1лвтология] Ж a v х

• ►    ►• Редукция импликации [Таи юлсм ия] ж a v х

2 ^автологир_} ф

• ▼    Раздел метазнаний ^ ^ Q ж а

• ►    Рефлексивность равенства [Метаматематическая аксиома; v х ►    *• симметричность равенства [Метаматематическая аксиома ж a v х ►    >• Транзитивность равенства [Метаматематическая аксиома] ж a v х ►    » Замена равных термов в формуле [Метаматемати* еская аксиома | Ж a v х ►    >- Грименение раьенсюа и равносильное i и с кванюром исеобщнос iи в формуле [Мегамагема ичеккая

аксиома] ж a v х

• ►    >- Перехэд к множес ту пси эжи юлы ьх чисел в киан юре сущее юэвания [Ме1амаюма1И’-ххкая аксиома] ж a v х

• ►    Переход к множеству отрицательных’-исел в кванторе существования [Метаматематическая аксиома; ж a v х

• ►    >- Переход к множес шу на i уралы ых чисе! и квашоре ыеобщнО'С in [Me гама гема 1ичес кая аксиома" ж a v х

• ►    >• П рименение равносильности с квантором всеобщности в формуле [Метама’емати'-есчая аксиома] ж a v х

• ►    *• Исключение квантора всеобщности год квантором суи|ествования [Метаматематическая аксиома] ж a v х

• ►    *• Исключение квантора существования [Метаматематическая аксиома; ж a v х

• ►    1 ереход к значению переменной в кванторе всеобп}ности [Метаматемати* еская аксиома| Ж a v х

• ►    ►• Определение квантора существования [Метаматематическая аксиома; ж a v х

• ►    ** Исключение квантора всеобщности [Метаматематическая аксиома| ж a v х

• ►    >• Добавление киан юра исеибщ1ЮС1 и [MfciaMaiема!ическая аксиома; Ж a v х

• ►    >• Замена значения на квантор существования [Метаматематическая аксиома, ж a v х

• ►    »• Примы ениераиносилыюс1и под кианюром сущее шования [Мс1ама1ема1ическая аксиома] ж a v х

• ►    *• Если хвост последовательности ограничен, то и вся последовательность ограничена [Метаматематическая аксиома] ж a v х

• ►    n- Переход к множеству отрицательных чисел в кванторе существования? [Метаматематическая аксиома; ж a v х

• ►    *• I рименение импликации к квантору существования [Метаматематическая эксиома Ж a v х

• ►    *• Замена равное ильных формул в формуле [Метаматематическая аксиома] ж a v х

• ►    *• I ереход под квантором суп.ествования от множества отрицательных к множеству положительных чисел [Meiамаюма!ическая аксиома] Ж a v х

Рисунок 11 – Начальное состояние базы способов рассуждений в интерфейсе средства портала « Редактор базы способов рассуждений »

Все подграфы, корневые вершины которых соответствуют вершинам « Предложение », « Тавтология » и « Метаматематическая аксиома » в соответствующих орграфах грамматик, отображаются в текстовом представлении. На рисунке 12 показан пример для пропозициональных тавтологий.

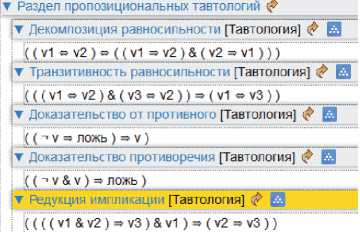
Рисунок 12 – Текстовое представление пропозициональных тавтологий в базе способов рассуждений в интерфейсе редактора « Редактор базы способов рассуждений »

Все редакторы и решатель задач оболочки включаются в состав программных компонентов портала знаний.

5    Использование текущего состоянием портала знаний исследователями

Для использования текущего состояния портала знаний по верификации математических доказательств пользователю сначала необходимо пройти процедуру регистрации на web-сайте платформы IACPaaS, после чего для него создаётся Личный кабинет , включающий Персональный Фонд . С помощью Системы управления пользователь может произвольным образом структурировать свой Персональный Фонд: создать древовидную структуру разделов.

Дальше у пользователя появляется возможность скопировать текущее состояние портала знаний из Фонда платформы в Персональный Фонд своего личного кабинета. Получение копии текущего состояния портала знаний состоит в следующем. В разделе Персонального Фонда « Загрузки » создаётся копия единицы хранения, представляющей решатель задач « Интерактивный верификатор доказательств ». При создании копии решателя он связывается с копией текущего состояния базы математических знаний, для которой метаинформацией (орграфом грамматики) является уже копия модели онтологии базы математических знаний; с копией текущего состояния базы способов рассуждений; а также со всеми остальными хранимыми в портале знаний единицами хранения, указанными в декларативной спецификации решателя задач « Интерактивный верификатор доказательств ». Полученные копии единиц хранения можно перенести из раздела « Загрузки », в нужные разделы Персонального Фонда. Редакторы соответствующих баз и модели онтологии базы математических знаний в силу способа своей реализации не копируются: они доступны из личных кабинетов и настроены уже на копии этих информационных компонентов.

Результатом выполнения операции копирования текущего состояния портала знаний является также создание в личном кабинете пользователя персонального прикладного сервиса. Создание сервиса подразумевает создание орграфа информации, представляющего персональное хранилище доказательств⁷, и его связывание с копией единицы хранения, представляющей решатель задач оболочки, с помощью которого это хранилище можно наполнять. Связывание состоит в создании специального вида единицы хранения, представляющей запускаемую и исполняемую на платформе IACPaaS сущность – сервис . На рисунках 13, 14 продемонстрированы примеры работы такого сервиса при формировании доказательства теоремы о том, что если последовательность имеет предел, то она является ограниченной.

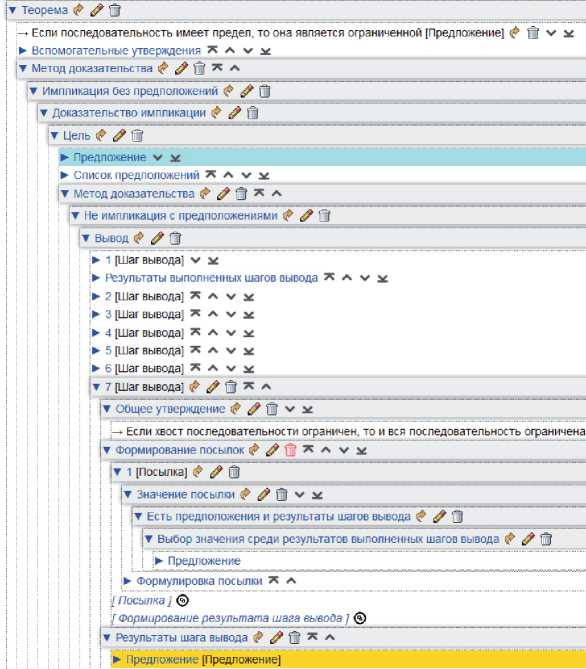
Рисунок 13 – Работа прикладного сервиса при формировании доказательства теоремы (пример)

С этого момента пользователь-исследователь может независимо развивать свою персональную базу математических знаний и базу способов рассуждений, а также язык представления математических знаний в Персональном Фонде с помощью соответствующих редакторов и доказывать математические утверждения.

6    Изменение текущего состояния портала знаний администратором

Изменение текущего состояния портала знаний может выполняться двумя способами: по инициативе пользователя либо по инициативе администратора. В обоих случаях для этого предназначен специальный сервис администратора, с помощью которого последний может получить доступ на чтение к персональным базам личных порталов пользователей. Данный сервис позволяет просматривать персональные базы математических знаний, показывая только те математические утверждения (вместе с разделами, в которых они находятся), доказательства которых являются полными. Эти доказательства должны быть рекурсивнополными, т.е. используемые в них математические утверждения, отсутствующие в общей базе математических знаний, тоже должны иметь полные доказательства.

Если в доказательствах используются способы рассуждений, отсутствующие в общей базе способов рассуждений, то они должны быть верифицированы администратором, прежде чем эти способы попадут в соответствующие общие базы.

Если при формулировке некоторых математических утверждений используются конструкции языка представления математических знаний, отсутствующие в общей онтологии базы математических знаний, и администратор согласен с этими утверждениями, то они включаются в общую онтологию.

▼ l(ei ь v' ^ (£f

► Г редпоженис v ^

► Список предлопожении ^ a v ^

▼ Метод доказательства ^ ^ ® х а

▼ le импликация с предположениями ^ ^ п

▼ Вывод ^ ^ ^

• ►    1 [Шаг вывода] v х

• ►    Результаты выполненных шагов вывода ^ a v ^

• ►    2 fl Itai вывода] ^ a v- ^

• ►    3 [Шаг вывода] ж a v х

• ►    4 filial вывода] ^ a v ^

• ►    5 {Шаг вывода] ^ a v ^

• ►    6 [Шаг вывода] х а \/ ^

• ▼    7 fl Itai вывода] ^ ^ \ ^ ^ ^/s

• ▼    Общее у1нерждение ^ ^ |fl| v х

—* Если xwx:i 11<х:педова1еньн(х:1И оцктичси, юи вся 1нх:1*щона1(М1Ы1(м:1Ь()|раничена

• ▼    Формирование лосьи эк ^ ^ "^ X a v х

• ▼ 1 ]П<х:ы1ка] ^ ^ И

• ▼ Значение посылки (^ ^ Т ^ х

▼ Есть предположения и результата шагов вывода ^ ^ *5

▼ Выбор значения среди результатов выполненных шагов вывода (► ^ @

► Предложение

► Формулировка н:кнл ки ^ *

г Пост;?' ! / ®

Получить результат текущего шага вывода

:' ребуется еде один шаг вывода

Закрель ]

▼ RriyiibiaiM пила вывода ^ ^ f?] ^ а

► Г|иуию;к(п ие ГП|ху|нож'м и-']

• г Лредложенб/е 7 ф®

(Шаг «ыаода j ®

► Единственность предела последовательности [Доказательство] ^ а [Доказательство ] (5)

Рисунок 14 – Результат работы агента «Формирователь результата шага вывода» (пример)

Заключение

В работе представлена концептуальная архитектура оболочки для интерактивных систем верификации математических доказательств и создаваемого с её помощью развиваемого тематического портала знаний. Описан процесс реализации всех программных и информационных компонентов оболочки на облачной платформе IACPaaS с использованием предоставляемых ею технологий и инструментальных средств их поддержки. Рассмотрен процесс разработки начального состояния портала знаний, способ использования текущего состояния портала знаний заинтересованными членами математического сообщества, а также механизмы изменения текущего состояния портала его администратором.

В основу оболочки и, как следствие, портала знаний положена явно представленная расширяемая формально-логическая система, приближенная к математической практике конструирования доказательств. Модель онтологии базы математических знаний, база математических знаний и база способов рассуждений расширяются с помощью соответствующих специализированных редакторов, входящих в состав портала знаний. При расширении модели онтологии новыми конструкциями языка представления знаний под эти изменения автоматически адаптируется управляемый ей соответствующий редактор, а решатель задач портала инвариантен по отношению к такому расширению.

В развитии портала знаний по верификации математических доказательств могут принимать участие все заинтересованные члены математического сообщества. Это осуществляется с помощью системы личных кабинетов платформы IACPaaS, в которых каждый пользователь может независимо развивать свою персональную копию текущего состояния общего портала знаний, и контролируется администратором портала знаний с помощью специального сервиса портала. Таким образом поддерживается синхронизация коллективного доступа к информационным компонентам общего портала и обеспечивается защита этих компонентов от их умышленного или непреднамеренного разрушения пользователями.

В результате развития портала может быть накоплена библиотека способов рассуждений, которыми математики пользуются в своей практике при доказательстве теорем. Эта библиотека может анализироваться специалистами по математической логике на предмет правильности содержащихся в ней способов рассуждений.

Работа выполнена при частичной поддержке РФФИ (проекты 17-07-00299 и 18-07-01079) и КПФИ «Дальний Восток» (проект 18-5-078).