Реализация параллельных вычислений в программном комплексе "LS-STAG_TURB" для моделирования течений вязкой несжимаемой среды на системах с общей памятью

Во многих инженерных приложениях возникает необходимость решения сопряженных задач гидроупругости. В качестве примеров можно привести

Puzikova V. Realization of parallel computations in the software package «LS-STAG_turb» for viscous incompressible flow simulation on systems with shared memory. Trudy ISP RAN/Proc. ISP RAS, 2016, vol. 28, issue 1, pp. 221-242 расчет обтекания роторов ветроэнергетических установок, труб теплообменников энергетических установок, удлиненных элементов конструкций зданий и сооружений, проводов линий электропередачи и т.п. Такие задачи из-за необходимости моделирования взаимного влияния течения жидкости и движения погруженного в нее тела являются достаточно сложными для численного решения и требуют применения высокоточных численных методов. Кроме того, поскольку из-за движения тела форма расчетной области изменяется в процессе расчета, при использовании сеточных методов с сеткой, связанной с телом, достаточно существенными становятся вычислительные затраты на перестроение сетки. Однако, существуют сеточные методы, в которых сетка не связана с границей тела и не изменяется на протяжении всего расчета, несмотря на движение обтекаемого тела. Такие методы относятся к классу методов погруженных границ [1]. Данные методы предполагают использование прямоугольных сеток. При пересечении прямоугольных ячеек сетки с границей области течения образуются ячейки неправильной формы, называемые усеченными. При использовании методов погруженных границ важно обеспечить высокую точность решения задачи именно в усеченных ячейках, поскольку на них задаются граничные условия, и, кроме того, решение вблизи границы обтекаемого тела (погруженной границы) может иметь большие градиенты.

К наиболее эффективным методам этого класса относят метод LS-STAG [2]. LS-STAG-сетка состоит из трех разнесенных сеток, ячейки которых представляют собой контрольные объемы для скоростей и давления. Для представления погруженной границы используется аппарат функций уровня [3], а LS-STAG-дискретизация производится по одним и тем же формулам, как в прямоугольных ячейках, так и в усеченных, причем шаблон дискретизации имеет в двумерном случае пятиточечную структуру. Все это позволяет значительно снизить затраты машинного времени на обработку усеченных ячеек. В работе [2] построена LS-STAG-дискретизация двумерных уравнений Навье - Стокса для вязкой несжимаемой среды. Автором настоящей статьи разработаны модификации метода LS-STAG, позволяющие использовать модели турбулентности Смагоринского, Спаларта - Аллмараса, к- £ , к-(О и к-ti) SST в рамках RANS, LES и DES подходов [4, 5], а также модификации метода LS-STAG для решения сопряженных задач гидроупругости [6]. Как и многие «нестандартные» высокоточные методы, метод погруженных границ LS-STAG не реализован в широко распространенных пакетах вычислительной гидродинамики, поэтому весьма актуальной задачей является разработка эффективной программной реализации метода LS-STAG и его модификаций.

Автором разработан программный комплекс «LS-STAG_turb» для моделирования движения профилей в потоке вязкой несжимаемой среды [7]. Программа написана на языке C++ и имеет объектно-ориентированную легко расширяемую структуру. Комплекс позволяет моделировать обтекание движущихся профилей произвольной формы, например вращение роторов ветроэнергетических установок. Кроме того, возможно моделирование обтекания систем, состоящих из любого числа подвижных профилей, имеющих одну или две степени свободы. Результаты верификации комплекса демонстрируют высокую точность метода LS-STAG и разработанных модификаций: удается качественно и количественно верно моделировать достаточно сложные и «тонкие» гидродинамические эффекты, например, эффект стабилизации следа за круговым профилем, совершающим высокочастотные вращательные колебания, известный как эффект Танеды [8, 9]. При этом для получения точных количественных результатов в случае моделирования явлений, отличающихся высокими скоростями движения профилей, и, соответственно, высокими значениями местного числа Рейнольдса, которые характерны, например, для ветрового резонанса профиля или системы профилей, необходимо сильное измельчение сетки, что приводит к резкому росту затрат вычислительных ресурсов. Для решения этой проблемы необходимо разработать параллельную версию программного комплекса «LS-STAG_turb».

Для распараллеливания вычислений при решении задач вычислительной механики часто используют методы декомпозиции области [10]. Идея методов декомпозиции заключается в том, что расчетная область разбивается на пересекающиеся или непересекающие подобласти и исходная задача представляется в виде совокупности вспомогательных краевых задач в этих подобластях. При этом на границах подобластей, совпадающих с границами исходной расчетной области, ставятся граничные условия из исходной задачи, а на остальных границах подобластей, называемых внутренними, ставятся условия сопряжения, которые записываются в виде граничных условий третьего рода. Решение вспомогательных задач может осуществляться параллельно, при этом эффективность полученного алгоритма зависит от многих факторов [11]: наличия и величины пересечения смежных подобластей, топологии декомпозиции области, типов граничных условий на внутренних границах подобластей, организации итерационных процессов, эффективности распараллеливания вычислений при решении вспомогательной задачи в подобласти. На LS-STAG-сетке дополнительные сложности также возникают из-за наличия твердых и усеченных ячеек и изменения их местоположения при перемещении подвижной погруженной границы. Таким образом, разработка параллельного алгоритма решения задачи методом LS-STAG, основанного на декомпозиции расчетной области, представляет собой предмет отдельного исследования. В рамках данной работы рассматриваются только вопросы оптимизации и распараллеливания вычислений при решении одной задачи в расчетной области без подобластей. Разработанные алгоритмы впоследствии также можно будет применять для эффективного решения вспомогательнх задач в подобластях.

2.    Программный комплекс «LS-STAG_turb»

Общая схема работы программного комплекса «LS-STAG_turb» представлена на рис. 1. В блоке Б1 происходит заполнение полей структуры описания задачи из файла с постановкой, инициализация сервисной информации (текущее время, номер итерации, пути к папкам с результатами), открытие лог-файла, инициализация экземпляров структур, реализующих работу с решениями, LS-STAG-сеткой и разностыми аналогами решаемых уравнений. Затем запускается процесс моделирования: до выполнения заданного числа шагов по времени выполняются блоки Б2-Б7.

Инициализация расчета

/Моделирование пока число шагов по⁴ | времени меньше заданного значения

Границы движутся'

Перестроение функции уровня

НетК

Пересчет правых частей СЛАУ

Решение СЛАУ

Коррекция решений

Рассчитать нагрузки?

Нет

Сохранить результаты?"

Нет

Расчет нагрузок

Сохранение результатов моделирования

Увеличиваем счетчик числа шагов по времени

Выход

Рис. 1. Блок-схема работы программного комплекса «LS-STAGturb» Fig. 1. Block diagram of the «LS-STAGturb» software system

Моделирование

При моделировании движения погруженных границ в блоке Б2 происходит пересчет функции уровня и зависящих от нее характеристик сетки. В комплексе «LS-STAG_turb» реализован алгоритм построения функции уровня для профиля произвольной формы при помощи аппроксимации границы кривой Безье [12], что позволяет моделировать обтекание профилей сложной формы и их систем (рис. 2).

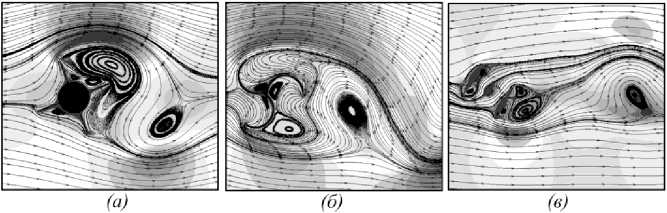
Рис. 2. Авторотация профилей различных форм, смоделированная в программном комплексе «LS-STAGturb»: (а) пропеллер с четырьмя лопастями; (б) ротор Савониуса с тремя лопастями; (в) ротор Дарье с двумя лопастями в форме симметричного крылового профиля ЦАГИ серии В с относительной толщиной 20 %

Fig. 2. Autorotation of profiles of differoent shapes, modeled in the «LS-STAGturb» software package: (a) propeller with four blades; (6) Savonius rotor with three lobes; (в) Darrieus rotor with two blades in the form of a symmetrical airfoil TsAGI of В Series with a relative thickness of 20°о

При моделировании движения погруженных границ перед пересчетом правых частей решаемых систем линейных алгебраических уравнений в блоке БЗ также происходит решение разностных аналогов уравнений движения обтекаемого профиля или системы профилей и пересчет матриц разностных аналогов операторов и предобуславливателей. Все эти операции выполняются в методе solve() базовой структуры DiscreteEquationlnterfасе, реализующей работу с разностными аналогами уравнений, перед решением систем линейных алгебраических уравнений (блок Б4). На каждом шаге по времени происходит решение двух разностных аналогов уравнения Гельмгольца для прогнозов скоростей и одного разностного аналога уравнения Пуассона для поправки давления. Значения скоростей и давления на текущем шаге по времени получаются после коррекции полученных прогнозов и поправок в блоке Б5. Помимо этого при использовании моделей турбулентности в блоке Б5 происходит решение разностных аналогов уравнений из используемой модели турбулентности и расчет рейнольдсовых или подсеточных напряжений, которые учитываются при пересчете правых частей систем для прогнозов скоростей на следующем шаге по времени. В зависимости от информации из структуры с описанием постановки задачи после этого может быть произведен расчет действующих на погруженные границы со стороны потока сил (блок Б6) или осуществлено сохранение в файл результатов моделирования и текущего состояния расчета (блок Б7). По окончании процесса моделирования происходит запись в лог-файл данных о времени завершения расчета и его продолжительности.

Для верификации разработанного программного комплекса «LS-STAG_turb» использовались тестовые задачи о моделировании обтекания неподвижных и движущихся профилей различных форм. В частности, смоделирован 225

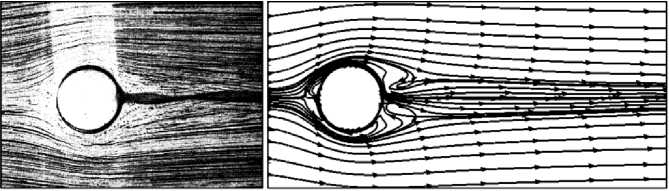
Puzikova V. Realization of parallel computations in the software package «LS-STAG_turb» for viscous incompressible flow simulation on systems with shared memory. Trudy ISP RAN/Proc. ISP RAS, 2016, vol. 28, issue 1, pp. 221-242 наблюдавшийся в эксперименте [8] эффект стабилизации следа за профилем, совершающим высокочастотные вращательные колебания, известный как эффект Танеды и редко воспроизводимый численно (рис. 3). Все результаты верификационных расчетов хорошо согласуются с известными в литературе экспериментальными и расчетными данными.

(а)                                            (б)

Рис. 3. Стабилизация следа за круговым профилем.

совершающим высокочастотные вращательные колебания при Re = 111: (а) эксперимент [8]; (б) расчет методом LS-STAG

Fig. 3. Track stabilization of circular profile committing high-frequency rotational oscillations at: (A) experiment [8]: (B) calculation with methodLS-STAG

Помимо моделирования течений вязкой несжимаемой среды, описываемых уравнениями Навье - Стокса, программный комплекс «LS-STAG_turb» позволяет проводить расчеты с использованием моделей турбулентности Смагоринского, Спаларта - Аллмараса, k-s, к-б) и к-а> SST в рамках RANS, LES и DES подходов к моделированию турбулентности. Пример такого расчета представлен на рис. 4. Также имеется возможность моделирования обтекания профилей и их систем, имеющих 1 или 2 степени свободы (рис. 5). Как было отмечено выше, для получения точных количественных результатов в задачах такого плана необходимо сильное измельчение сетки, приводящее к резкому росту вычислительных затрат. Решением данной проблемы может служить распараллеливание вычислений.

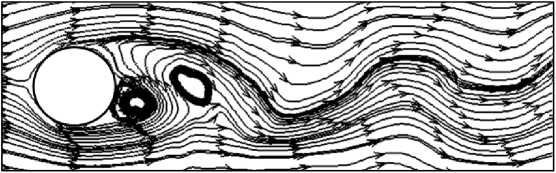
Рис. 4. Обтекание кругового профиля при Re = 3900, смоделированное в программном комплексе «LS-STAG turb» с использованием модели турбулентности Спаларта - Аллмараса в рамках подхода RANS

Fig. 4. Flow around a circular profile with Re = 3900 modeled in the software package «LS-STAGturb» using Spalart—Allmaras turbulence model with approach RANS

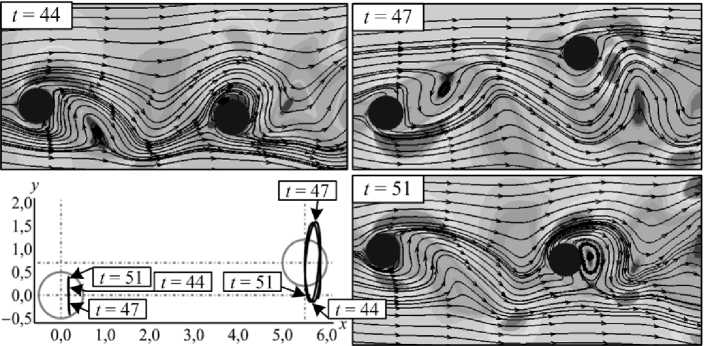
Рис. 5. Ветровой резонанс системы из двух круговых профилей, расположенных под углом выноса и имеющих 2 степени свободы, при Re = 100, смоделированный в программном комплексе «LS-STAGturb»: траектории движения центров профилей и линии тока в моменты времени 1 = 44, t = 47 и / - 5 I

Fig. 5. Wind resonance of a system of two circular prof les placed at an angle of cartying out and having two degrees of freedom, when modeled in the software package «LS-STAGturb»: trajectory profiles centers and line offlow at times t = 44, t = 47, and t = 51

3.    Постановка тестовой задачи и используемые аппаратно-программные средства

В качестве задачи для тестирования эффективности разрабатываемых параллельных алгоритмов рассмотрим задачу о моделировании обтекания кругового профиля диаметра D, совершающего в невозмущенном потоке вынужденные поперечные колебания по закону

-^С =

₀ J            A,         KYODIV^,

Yc~Yc + Ucos(2^Se[Hy-10D]/D), t >Y0D/K„, где A - амплитуда колебаний кругового профиля, 5 - кинематическое число Струхаля, (Х°,У°) - координаты центра профиля в среднем положении, (ХС,УС) - координаты центра профиля в текущий момент времени, У„ -скорость набегающего горизонтального потока, t - безразмерное время. При тестировании модификаций программного комплекса и параллельных алгоритмов будем моделировать 30 единиц безразмерного времени на

Puzikova V. Realization of parallel computations in the software package «LS-STAG_turb» for viscous incompressible flow simulation on systems with shared memory. Trudy ISP RAN/Proc. ISP RAS, 2016, vol. 28, issue 1, pp. 221-242 неравномерной сетке 240x296 (линейный размер ячейки сетки вблизи границы профиля Һ = 0,03125) с шагом по времени Л? = 0,005 при А = 0,2D, D = l,0, Г„=1,0, Re = 185, 5_e/Sh = l,2, где Re - число Рейнольдса, Sh ~ 0,201 - число Струхаля (безразмерная частота схода вихрей), вычисленное при данном значении числа Рейнольдса для неподвижного профиля. Далее эту тестовую задачу будем обозначать VerOscTest.

Тестирование проводилось на рабочей станции, построенной на платформе Intel Н81 с использованием двухъядерного процессора Intel Core ІЗ-4350Т (Haswell) с поддержкой HyperThreading (4 логических ядра), работающего на частоте 3100 МГц. Рабочая станция оснащена 8ГБайт оперативной памяти DDR3-1333, SSD-накопителем Crucial объемом 128 ГБайт и жестким диском Seagate объемом 1 ТБайт. Внешние графические карты в рабочей станции не использовались. Далее эту рабочую станцию будем обозначать РС1.

Для исследования масштабируемости алгоритмов помимо РС1 также использовалась рабочая станция, построенная на платформе Intel Z97 с использованием 4-ядерного процессора Intel Core І7-4790К (Devil's Canyon) с поддержкой технологии HyperThreading (8 логических ядер), работающего на частоте 4400 МГц. Рабочая станция оснащена 16 ГБайт оперативной памяти DDR3-1600 и двумя SSD-накопителями Crucial объемом 256 ГБайт и 1 ТБайт. Внешние графические карты в рабочей станции не использовались. Данную рабочую станцию будем обозначать РС2.

Время решения тестовой задачи последовательным программным комплексом «LS-STAG_turb», при разработке которого использовался компилятор Microsoft Visual Studio 2010, на PCI составляет 4666 с. Использование вместо этого компилятора оптимизирующего компилятора Intel C++ 15.0 позволяет без модификаций исходного кода уменьшить время счета на 0,5 %. Включение опции компилятора /МТ предписывает приложению использовать многопоточную статическую версию библиотеки времени выполнения и разрешает дополнительные оптимизации компилятора, использующие многопоточность. После включения этой опции время решения тестовой задачи VerOscTest на РС1 составило 3968 с. Таким образом, время проведения расчета удалось сократить на 15 %. При проведении дальнейших экспериментов по оптимизации программы и распараллеливанию вычислений будем использовать компилятор Intel C++ 15.0 с опцией /МТ.

• 4.    Оценка эффективности распараллеливания вычислений Определим, какие вычисления имеет смысл распараллелить в первую очередь. Для этого необходимо выделить участки программы, на выполнение которых расходуется наибольшее количество времени. Полная структура временных затрат при решении тестовой задачи VerOscTest (рис. 6) была определена с помощью профилировщика AMD CodeAnalyst [13]: 48,0 % времени работы программы занимает выполнение умножения разреженной матрицы на вектор

(операция 1), а 34,5 % - решение систем линейных алгебраических уравнений с трехдиагональными матрицами методом прогонки при выполнении сглаживания в многосеточном предобуславливателе (операция 2). Решение систем линейных алгебраических уравнений методом BiCGStab без учета затрат времени на работу предобуславливателей (операция 3) занимает 16,5 % времени выполнения расчета, прочие операции - 1 %.

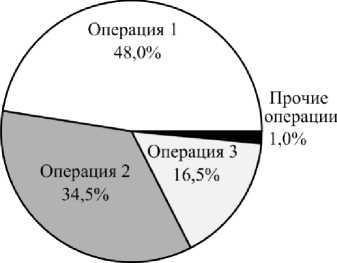
Рис. 6. Структура временных затрат при решении тестовой задачи VerOscTest

Fig. 6. Structure of time spent in solving test problem VerOscTest

Поскольку внутри операции 3 выполняются различные операции над векторами (вычисление скалярного произведения, нормы вектора и т.д.), сначала сосредоточимся на распараллеливании операций 1 и 2. Оценим максимальное ускорение, которое можно получить при распараллеливании только операции 1 или операций 1 и 2, при помощи закона Амдала [14], который гласит, что для системы из 5 вычислительных ялер максимально возможное ускорение программы с долей Р параллельного кода и (1-Р)

последовательного кода равно а = 1/((1-P) + P/S'). Полученные оценки приведены в табл. 1. Они соответствуют случаю идеального (линейного) распараллеливания, при котором параллельный код на вычислительной системе с 5 ядрами выполняется в 5 раз быстрее. Реальное ускорение будет ниже, поскольку при переходе от последовательной программы к параллельной добавятся накладные расходы на поддержку многопоточных вычислений: расходы на создание задач и потоков, расходы на работу планировщика потоков, расходы на запуск и синхронизацию потоков, коммуникационные издержки на передачу информации между потоками, издержки в виде дисбаланса загрузки ядер из-за точек синхронизации или конфликтов в конвейере процессора и планировщике операционной системы. Далее для распараллеливания вычислений будем использовать такие технологии параллельного программирования, как Intel® Cilk™ Plus [15], Intel® TBB [16], OpenMP (реализация из Intel® Parallel Studio ХЕ 2015, стандарт 4.0). Эти технологии предполагают, что пользователь при помощи ключевых слов лишь обозначает задачи, выполняемые параллельно, а организация управления потоками и работы с ними определяются самой технологией. Таким образом, вышеперечисленные накладные расходы на поддержку многопоточности, а, значит, и реальное ускорение, зависят от используемой технологии параллельного программирования.

Табл. 1. Максимально возможное ускорение при распараллеливании операций 1 и 2

Table. 1. The maximum possible acceleration when parallelizing operations 1 and 2

Распараллеливаемые операции	Р	Максимальное ускорение, раз
		2 ядра	4 ядра	8 ядер
1	0,480	1,316	1,563	1,724
1,2	0,825	1,702	2,623	3,596

Получить оценки ожидаемого ускорения в зависимости от используемой технологии параллельного программирования позволяет инструмент Intel® Advisor [17]. Для этого необходимо подключить заголовочный файл advisor-annotate. Һ и выделить содержимое операции при помощи команд ANNOTATE_SITE_BEGIN() И ANNOTATE_SITE_END() . Для операции 1 таким образом было получено, что наибольшее ускорение при использовании любой из трех рассматриваемых технологий прогнозируется при расчете на системе с четырьмя ядрами. Согласно прогнозу, использование ОрепМР и Intel® ТВВ приведет к замедлению работы программы, a Intel® Cilk™ Plus - к незначительному ускорению (на 20 %). Тем не менее, поскольку оценки Intel® Advisor являются приблизительными, представляется целесообазной поддержка в разрабатываемом приложении всех перечисленных технологий параллельного программирования и переключение между ними при помощи директив препроцессора по определениям LS_STAG_USE_CILK, LS_STAG_USE_OMP И LS_STAG_USE_TBB.

5.    Оптимизация и распараллеливание вычислений

Произведем преобразование последовательного кода в параллельный при помощи рассматриваемых технологий параллельного программирования на примере операции 1 - умножения разреженной матрицы на вектор, хранящийся в массиве multiplier, с сохранением результата в массив Vector. Разреженная матрица хранится в формате CSR[18]: элементы матрицы хранятся в массиве m_Cell, портрет - в массиве m_Portrait, а индексы элементов, с которых начинаются строки матрицы - в массиве m_Num. Последовательная реализация метода имеет следующий вид: for(int i = 0; i < size; i++)

{ double aux = 0.0;

for(int j = m Num[iJ; j < m Num[i+1]; j++)

aux += m Cell[j] * multiplier[m Portrait [ j]];

Vector[i] = aux;

};

Итерации внешнего цикла являются независимыми, поэтому для распараллеливания вычислений достаточно при использовании технологии Intel® Cilk™ Plus вместо for написать cilk_for, а при использовании ОрепМР - перед for поставить #pragma omp parallel for. При использовании технологии Intel® ТВВ код параллельной версии данного метода получается более громоздким, но при помощи лямбда-выражений из стандарта С++11 его можно записать следующим образом:

{ for(int i = r.begin(); i < r.end(); i++)

{ double aux = 0.0;

for(int j = m Num[i]; j < m Num[i+1]; j++) aux += m Cell[j] * multiplier[m Portrait [ j]];

Vector[i] = aux; }

}                                       )

Количество ядер для Intel® Cilk™ Plus и ОрепМР задается при помощи cilkrts set param и omp set num threads соответственно, а для Intel® TBB указывается при создании планировщика - экземпляра класса tbb::task scheduler init.

Поскольку Intel® Advisor показал, что оптимальным является использование вычислительной системы из четырех ядер, тестовая задача VerOscTest была решена на РС1 с использованием четырех логических ядер при помощи программы с распараллеленной операцией 1. Время счета и достигнутое ускорение представлено в табл. 2. Наибольшее ускорение, достаточно близкое к полученной по закону Амдала оценке (в 1,563 раза), достигнуто при использовании Intel® Cilk™ Plus. При этом для всех трех технологий полученные ускорения достаточно сильно превышают оценки Intel® Advisor. Также не подтвердился прогноз Intel® Advisor о том, что технология Intel® ТВВ позволит получить большее ускорение, чем ОрепМР. Это свидетельствует о целесообразности предусмотренной в разработанном программном комплексе возможности задания используемой технологии параллельного программирования при помощи определений препроцессора.

Табл. 2. Время счета на РС1 с использованием 4 логических ядер и ускорение при распараллеливании операции 1

Table. 2. Time of calculatiion on PCI with 4 logical cores and acceleration when parallelizing operations 1

Технология	Intel® Cilk™ Plus	ОрепМР	Intel® ТВВ
Время счета, с	2548	2713	2870
Ускорение, раз	1,557	1,463	1,383

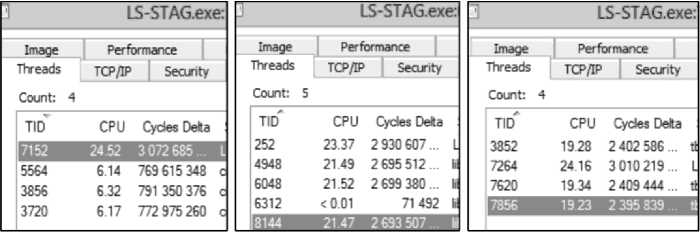
Сравним также работу планировщиков (диспетчеров) потоков рассматриваемых технологий параллельного программирования. Для этого используем программу ProcessExplorer [19], предназначенную для мониторинга процессов в системе. Информация о потоках приложения при расчете на четырех логических ядрах представлена на рис. 7.

(и)                             (б)                              (в)

Рис. 7. Информация о потоках приложения при расчете на четырех логических ядрах с использованием: (a) Intel'® Cilk™ Plus: (б) ОрепМР: (в) Intel® ТВВ

Fig. 7. Information about the application threads based on four logical cores using: (a) Intel® Cilk ™Plus: (б) ОрепМР: (e) Intel® TBB

При использовании рассматриваемых технологий потоки создаются один раз, поскольку их идентификаторы (TID) не изменяются на протяжении всего расчета. При этом диспетчеры потоков работают в основном потоке приложения, однако диспетчер потоков ОрепМР создает дополнительный дочерний поток (на рис. 7, б это поток с TID, равным 6312), который занимается мониторированием рабочих потоков (судя по низкой загрузке потока - обслуживанием конфликтов). В результате на основной диспетчер потоков ОрепМР ложатся дополнительные накладные расходы по обслуживанию этого мониторирующего потока, что, по-видимому, приводит к увеличению времени проведения расчета и к меньшему по сравнению с Intel® Cilk™ Plus ускорению (табл. 2). Тем не менее, время счета при использовании ОрепМР оказалось меньше, чем при использовании Intel® ТВВ. Это свидетельствует о том, что основной диспетчер потоков ОрепМР из Intel Parallel Studio 2015 реализован достаточно эффективно. Также необходимо отметить, что при использовании технологии Intel® Cilk™ Plus время проведения расчета оказалось наименьшим, хотя загрузка ядер рабочими дочерними потоками приложения была примерно в 3 раза ниже, чем при 232

использовании ОрепМР и Intel® ТВВ. Из этого можно сделать вывод, что диспетчер потоков Intel® Cilk™ Plus эффективно управляет средствами конвейеризации и кеширования процессора, снижая нагрузку на ядра, а также берет на себя большую часть затрат по управлению критическими секциями, семафорами и другими средствами синхронизации потоков, в то время как планировщики потоков ОрепМР и Intel® ТВВ часть функций синхронизации перекладывают на рабочие дочерние потоки, отрывая их от основной работы и создавая большую загрузку ядер при меньшей эффективности.

Перейдем к распараллеливанию операции 2 - сглаживающих итераций многосеточного решателя. В качестве сглаживателя используется метод ADLJ - Alternating Damped Line Jacobi [20]. Данный метод предполагает решение систем линейных алгебраических уравнений с трехдиагональными матрицами, сформированными из матрицы исходной системы. Для полученных матриц хранится LU-разложение в массивах L, D и U (нижняя, главная и верхняя диагонали соответственно). Алгоритм вычисления решения sol системы с построенной трехдиагональной матрицей и правой частью right_side имеет следующий вид:

sol[0] = right_side[0] / D[0] ;

for(int 1=1, г = 0; 1 < NM; 1++, r++)

sol[i] = (right_side[1] - L[r] * sol[r]) / D[i] ;

for(int 1 = NM - 2; 1 > -1; 1--) sol[i] -= U[i] * sol[i+l];

В таком виде алгоритм не может быть распараллелен, поскольку итерации циклов являются зависимыми: при вычислении значения элемента sol[i] используются значения sol [г] и sol [1 + 1], полученные на предыдущих итерациях. Однако, поскольку исходная матрица была получена при дискретизации с пятиточечной структурой шаблона на прямоугольной сетке NxM, сформированная из нее трехдиагональная матрица распадается на М независимых блоков размера NxN, и алгоритм может быть переписан следующим образом:

for(int j = 0; j < М; j++) // блоки

{ int q = j * N; // номер первой строки блока sol[q] = right_side[q] / D[q];

for(int r = q, 1 = r + 1; 1 < r + N; 1++, r++)

sol[i] = (right_side[1] - L[r] * sol[r]) / D[i];

for(int q2 = q - 1, 1 = q2 + N - 1; 1 > q2; 1--) sol[i] -= U[i] * sol[i+l];

}

Теперь итерации внешнего цикла являются независимыми, и его можно распараллелить аналогично циклу из операции 1. В табл. 3 представлены

Puzikova V. Realization of parallel computations in the software package «LS-STAG_turb» for viscous incompressible flow simulation on systems with shared memory. Trudy ISP RAN/Proc. ISP RAS, 2016, vol. 28, issue 1, pp. 221-242 значения времени счета и достигнутых ускорений при решении задачи VerOscTest на РС1 при помощи программы с распараллеленными операциями 1 и 2. Наибольшее ускорение, достаточно близкое к оценке по закону Амдала (в 2,623 раза), как и в случае распараллеливания операции 1, достигнуто при использовании технологии Intel® Cilk™ Plus.

Табл. 3. Время счета на РС1 с использованием четырех логических ядер и ускорение при распараллеливании операции 1 и 2

Table. 3. Time of calculatiion on PCI with 4 logical cores and acceleration when parallelizing operations 1 and 2

Технология	Intel® Cilk™ Plus	OpenMP	Intel® TBB
Время счета, с	1547	1698	1774
Ускорение, раз	2,565	2,337	2,237

После распараллелиливания двух наиболее трудоемких операций было произведено распараллеливание ряда операций с векторами, на которые приходится большая часть времени выполнения операции 3, и перестроение некоторых разреженных матриц и сеточных функций, происходящее при движении погруженной границы. Помимо продемонстрированного на примере операции 1 распараллеливания цикла for с независимыми итерациями, использовались приемы распараллеливания циклов с редукцией. Покажем различия в распараллеливании циклов такого типа при использовании различных технологий параллельного программирования на примере распараллеливания расчета евклидовой нормы вектора, элементы которого хранятся в массиве Vector: double getNormO { ElemType aux = 0;

for(int 1=0; i < size; 1++)

{ ElemType cur = Vector[1]; aux += cur * cur; } return sqrt((double)aux);

}

При использовании OpenMP перед ключевым словом for необходимо добавить директиву #pragma omp parallel for reduction (+: aux). При использовании технологии Intel® Cilk™ Plus алгоритм принимает следующий вид: double getNormO

{ cilk::reducer<:op add="">> aux(0); cilk for(int i = 0; i < size; i++)

{ ElemType cur = Vector[i]; *aux += cur * cur; } return sqrt((double)aux.get_value() ) ;

}

for(int 1 = r.begin(); 1 < r.end(); 1++)

{ ElemType cur = Vector[1]; aux += cur * cur; } return aux;

}, [](ElemType x, ElemType y)->ElemType

{ return x + y; } ) ; return sqrt((double)res);

}

Кроме того, была проведена оптимизация кода. После этого время выполнения расчетов значительно уменьшилось даже при использовании одного ядра (табл. 4). Поскольку диспетчеры потоков Intel® Cilk™ Plus, ОрепМР и Intel® ТВВ не отключаются при работе приложения на одном ядре, особенности их работы, рассмотренные выше, напрямую сказываются на быстродействии даже в однопоточной версии. Таким образом, представленные в табл. 4 данные подтверждают предположение о том, что диспетчер потоков Intel® Cilk™ Plus реализован эффективнее планировщиков потоков ОрепМР и Intel® ТВВ.

Табл. 4. Время счета на РС1 с использованием одного ядра и полученное в результате оптимизации кода ускорение

Table. 4. Prime of calculation on PCI using a single core and the acceleration with code optimization

Технология	Intel® Cilk™ Plus	ОрепМР	Intel® ТВВ
Время счета, с	1958	2207	2318
Ускорение, раз	2,027	1,798	1,712

Для исследования масштабируемости комплекса была проведена серия вычислительных экспериментов (рис. 8). Наименьшее время проведения расчета независимо от технологии параллельного программирования и на PC 1, и на РС2 получается при использовании четырех логических ядер. На РС2, так же как и на РС1, при расчете на одном ядре быстродействие приложения, использующего Intel® Cilk™ Plus, оказывается выше чем у приложения, использующего ОрепМР, а дольше всего решение тестовой задачи VerOscTest идет при использовании Intel® ТВВ. Однако приложение с Intel® Cilk™ Plus на

Puzikova V. Realization of parallel computations in the software package «LS-STAG_turb» for viscous incompressible flow simulation on systems with shared memory. Trudy ISP RAN/Proc. ISP RAS, 2016, vol. 28, issue 1, pp. 221-242 обеих рабочих станциях масштабируется хуже приложения, в котором используется ОрепМР, а оно, в свою очередь, - хуже приложения с Intel® ТВВ. Из-за этого при проведении расчета с использованием четырех логических ядер на РС1 получаем, что приложение с Intel® ТВВ опережает приложение с ОрепМР (при этом наименьшее время счета получается по-прежнему при использовании Intel® Cilk™ Plus), а на РС2 приложение, использующее ОрепМР, по быстродействию опережает приложение с Intel® Cilk™ Plus, уступающее и приложению с Intel® ТВВ. Таким образом, подтверждается необходимость поддержки программным комплексом всех рассматриваемых технологий параллельного программирования и возможности выбора пользователем используемой технологии.

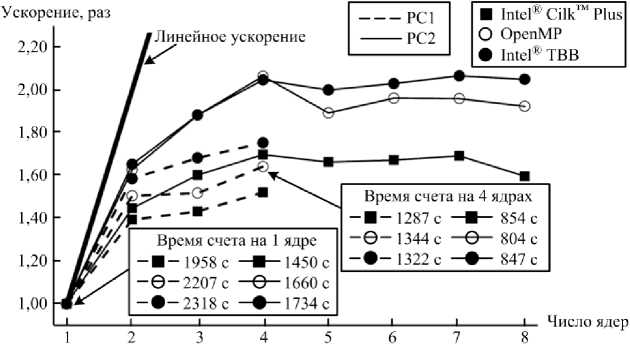
Рис. 8. Масштабируемость программного комплекса «LS-STAGturb» после оптимизации кода и распараллеливания операций

Fig. 8. Scalability of the «LS-STAGturb» software complex after the code optimization and parallelization of operations

6.    Выбор решателя и исследование эффективности его реализации

Также возможно уменьшение продолжительности расчета за счет модификаций решателя. В описанных выше экспериментах для решения систем линейных алгебраических уравнений использовался метод BiCGStab [20] (метод бисопряженных градиентов со стабилизацией) с предобуславливанием. Для разностного аналога уравнения Гельмгольца использовалось ILU-предобуславливание [18], а для разностного аналога уравнения Пуассона - многосеточное предобуславливание [20]. При этом на задаче VerOscTest решение разностных аналогов уравнения Гельмгольца (70744 и 70800 уравнений) с точностью б'-10 6 получается за 2 итерации, а решение разностного аналога уравнения Пуассона (70744 и 70800 уравнений) с той же точностью - за 7-20 итераций.

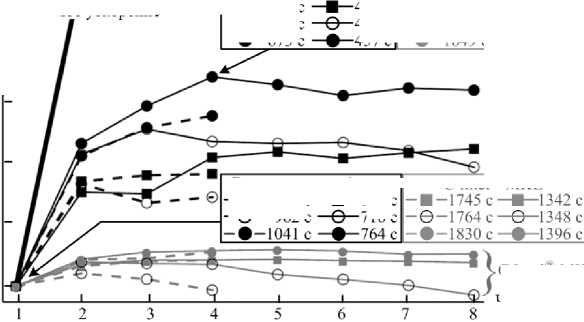
Заменим метод BiCGStab на метод FGMRES (гибкий метод обобщенных невязок) без изменения предобуславливателей. Метод FGMRES, как и метод BiCGStab, относится к методам крыловского типа [20]. Основное различие между этими двумя методами заключается в способе построения базиса в подпространстве Крылова: в методе BiCGStab для этого используется биортогонализация Ланцоша, а в FGMRES - ортогонализация Арнольди [20]. После оптимизации и реализации алгоритма метода FGMRES [20] была проведена серия вычислительных экспериментов для исследования масштабируемости алгоритма (рис. 9, черные линии). Использование разработанной реализации метода FGMRES позволило получить ускорение по сравнению с решением систем методом BiCGStab на одном ядре в среднем в 2,235 раза, а на четырех логических ядрах - в 1,829 раза, поскольку программа с новым решателем несколько хуже масштабируется. При этом решение разностного аналога уравнения Гельмгольца при использовании как метода BiCGStab, так и метода FGMRES получается за 2 итерации, в то время как решение разностного аналога уравнения Пуассона при использовании метода FGMRES получается за 4-7 итераций, что говорит о более быстрой сходимости метода FGMRES по сравнению с методом BiCGStab.

Ускорение, раз

С Intel8 MKL

Время счета на 4 ядрах

489 с

457 с

-Ө-1786С

-•-1649 с

1259 с

1253 с

-Ө-748 с

-•-673 с

---РС1

----РС2

Линейное ускорение

1,80 -

1,60

1,40

1.20

1,00

716 с

■ Intel® Cilk™ Plus

О OpenMP

• Intel® IBB

С Intel® MKL

Число ядер

Рис. 9. Масштабируемость комплекса «LS-STAGturb» при решении тестовой задачи VerOscTest (черные линии) и сравнение с решателем из Intel'® MKL (серые линии) Fig. 9. Scalability’ of the «LS-STAGturb» complex in solving the test problem VerOscTest (black lines) and the comparison with the solver from the Intel® MKL (gray lines)

Время счета на I ядре

С Intel" MKL

-Ө- 962 с

Наилучшее быстродействие при расчетах на одном ядре демонстрируют приложения, использующие технологию Intel® Cilk™ Plus, однако при расчете на РС2 с четырьмя ядрами благодаря хорошей масштабируемости наименьшая

Puzikova V. Realization of parallel computations in the software package «LS-STAG_turb» for viscous incompressible flow simulation on systems with shared memory. Trudy ISP RAN/Proc. ISP RAS, 2016, vol. 28, issue 1, pp. 221-242 продолжительность расчета получается при использовании Intel® ТВВ. Отметим, что по сравнению с исходным последовательным кодом время проведения расчета уменьшилось примерно в 5 раз при использовании одного ядра и в 7 раз при использовании четырех ядер.

Сравним эффективность разработанного решателя с аналогом из библиотеки Intel® Math Kernel Library (MKL) 11.2 [21], содержащей реализацию метода FGMRES. Эта библиотека оптимизирована для работы с разными процессорами Intel и обеспечивает использование их расширенных возможностей. Из предобуславливателей Intel® MKL содержит только ILU-предобуславливание, поэтому используем его для решения не только разностного аналога уравнения Гельмгольца, но и для решения разностного аналога уравнения Пуассона. При этом число итераций, совершаемых при решении разностного аналога уравнения Пуассона, возрастает до 25-140. Масштабируемость полученного алгоритма оказывается очень низкой (рис. 9, серые линии), поэтому на четырех ядрах он значительно уступает разработанному решателю. Использование собственной реализации метода FGMRES позволило получить ускорение по сравнению с решателем из Intel® MKL на одном ядре в среднем в 1,869 раза, а на четырех ядрах - в 2,526 раза.

7.    Заключение

Разработан параллельный программный комплекс «LS-STAG_turb» для моделирования движения профилей в потоке вязкой несжимаемой среды. В данном комплексе реализован высокоточный метод погруженных границ LS-STAG и разработанные модификации данного метода для и решения сопряженных задач гидроупругости с использованием моделей турбулентности Смагоринского, Спаларта - Аллмараса, k- s, k-ti) и к-а> SST в рамках RANS, LES и DES подходов к моделированию турбулентности. Разработанный программный комплекс поддерживает использование таких технологий параллельного программирования, как Intel® Cilk™ Plus, Intel® ТВВ и ОрепМР. Использование метода FGMRES для решения систем линейных алгебраических уравнений позволило достичь существенного сокращения времени проведения расчета (примерно в 2 раза) по сравнению с методом BiCGStab. Кроме того, разработанная программная реализация метода FGMRES оказалась эффективнее аналогичного решателя из библиотеки Intel® MKL, как при проведении расчетов на одном ядре, так и при использовании нескольких ядер.

Главным направлением дальнейшего развития параллельного программного комплекса «LS-STAG_turb» является разработка параллельного алгоритма решения задачи методом LS-STAG, основанного на декомпозиции расчетной области. При этом для эффективного решения вспомогательнх задач в подобластях будет использоваться представленная параллельная реализация решателя. Также планируется разработать препроцессор для подготовки файлов с исходными данными. Кроме того, в перспективе планируется разработка и реализация метода LS-STAG для решения трехмерных задач.