Regression Test Suite Prioritization using Residual Test Coverage Algorithm and Statistical Techniques
Автор: Abhinandan H. Patil, Neena Goveas, Krishnan Rangarajan
Журнал: International Journal of Education and Management Engineering(IJEME) @ijeme
Статья в выпуске: 5 vol.6, 2016 года.
Бесплатный доступ
Regression test suite study has been research topic for decades. In this paper we investigate the Regression test suite prioritization using residual test coverage algorithm for white box testing and introduce new statistical technique for black box testing. Our contribution in this paper is mainly problem solution to breaking the tie in residual coverage algorithm. Further we introduce new metric which can be used for prioritizing the regression test suite for black box testing. Towards the end part of the paper we get down to implementation details explaining how this can be done in the industrial or research project. The intended readers of this paper are developers and testers in the research field and practitioners of software engineering in the large scale industrial projects.
Residual Test Coverage Algorithm, CodeCover, Test Execution Time, Statistical Techniques
Короткий адрес: https://sciup.org/15014032
IDR: 15014032
Текст научной статьи Regression Test Suite Prioritization using Residual Test Coverage Algorithm and Statistical Techniques
We begin introduction of this paper with the statement, “Developer is also tester and vice versa” of Aditya P. Mathur [1]. A versatile software professional or researcher works in multiple capacities in a typical development life cycle. Missing exposure to either development or testing is partial view of the product development life cycle. The tester without development knowledge can contribute little towards the white box testing and developer without testing knowledge means quality compromise from the product perspective. With this precursor, it is clear that the paper is for both the testers and developers.
Regression testing is discussed at lengths in several papers. The main topics of research are: Test selection, minimization and prioritization. There are two measures of coverage
-
• Requirement coverage. In this method we trace the test cases to requirements and ensure that all the
* Corresponding author. Phone: +919886406214
requirements are covered. The requirement specification document itself serves as test oracle.
-
• Code coverage. In this method the measures such as statement coverage, branch coverage, loop coverage etc are checked to ensure that nothing is missed as part of testing.
Requirements coverage is not the topic of discussion in this paper. It’s the latter which will be focused as the same metric is used in the white box testing and black box testing approaches discussed in the further sections.
If P is the product code before bug fixes and enhancement and P’ is the product code after the modification, we can denote the corresponding test suites as T and T’ respectively. Now, one way to visualize T is as collection of obsolete, redundant and valid test cases. In other words T is collection of {obsolete, redundant, valid} test cases. The T’ will encompass {valid, newly added test cases}.
There are different schools of thoughts when it comes to selecting regression tests between successive releases. Each with their own set of advocates. As Aditya P. Mathur aptly classifies [1], the philosophy for each of these categories is very different. The categories are:
-
• Test all: Brute force method with long execution cycles. Most widely used technique in the commercial world combined with automation of regression testing
-
• Random selection: Sampling of the test cases. Better than no regression testing at all. Test cases are picked from the test suite except obsolete test cases randomly.
-
• Selecting modification traversing tests: Assumes the tester to have the knowhow of the complete product code. Better than test all and random selection process. Usually the testers classify the test cases in buckets where they put related test cases in a given bucket. Depending upon how the test cases are chosen this mode of testing may or may not yield good results.
-
• Test minimization: Pruning of the test suite by dropping the test cases with similar product trace code as they are redundant. This results in new reduced size of the regression test suite.
-
• Test Prioritization: Assumes that the test cases can be ranked on the basis of certain criteria.
It is the last school of thought which will be investigated in this paper. Regression test suite prioritization is must when there is crunch of resources and time.
In some organizations, the organizations may choose combination of the approaches mentioned above. Large execution time means test all approach and may mean drain of resources and time. Therefore good amount of research has already gone in optimizing the regression test suites.
In this paper we look at test prioritization using the approach which is implementable given time. The paper can be broadly classified into following sections:
-
• Residual test coverage algorithm enhancements for regression test suite prioritization using white box testing.
-
• Statistical techniques for regression test suite prioritization using black box testing.
-
• Process flow at the implementation level which can aid the above two processes.
-
• Case study of coverage tool to explain how metrics of choice can be extracted.
-
2. Residual Test Coverage Algorithm Enhancements for white Box Testing
As already explained earlier, if the current test suite is visualized as the collection of {obsolete, redundant, valid test cases}, the test suite for new version of the product will be {valid test cases, newly added test cases}. The new test cases added are with reason. They cover either the newly added functionality or they cover the modified functionality. In this case some of the valid test cases may become redundant or obsolete. In rare scenarios the obsolete test cases become valid test cases when the removed functionality is added back for some reason. In variably the newly added test cases go through the review process depending upon the organizations process in place. They are always executed. The remaining test cases need to be prioritized. We consider modified test cases as new test cases. Further, the approaches mentioned in further sections for black box and white box testing assume the historical data of the test suite is maintained between successive releases.
That is the coverage and execution time data of current suite becomes the reference data for the next build of the product. Since the new test cases are always executed, we are not ranking them among themselves. This means the test cases will be new test cases followed by prioritized test cases.
Since the newly added test cases will be far less compared to valid test cases taken from the previous release the following approaches should work in practical setup. The gain of ranking the new test cases is minimal as they are executed mandatorily.
We assume the reader of this paper is aware of residual test coverage algorithm. The concept behind the algorithm is explained nicely in the reference book [1]. The problem of breaking the tie is left to readers as an exercise. This is the problem definition which we will investigate. We there-fore modify the algorithm such that the random test selection is weeded out completely at all the steps.
The newly introduced parameters and steps by us are in italics. The modified algorithm looks as follows:
Algorithm for prioritizing the regression test suite post modification.
Input T’: Set of regression tests for the modified program P’.
entitiesCov: Set of entities in P covered by tests in T’.
cov: Coverage vector such that for each test t Ɛ T’, cov(t) is the set of entities covered by executing P against t.
executionTime: executionTime(t) is the time taken by the test case t Ɛ T’ to complete the execution.
linesOfCodeTraced: linesOfCodeTraced(t) is the total lines of product code covered by the test case t Ɛ T’ during execution.
Output PrT: A sequence of prioritized test cases such that (a) each test case belongs to T’, (b) each test in T’ appears exactly once in PrT, and (c) tests in PrT are arranged in the ascending order of cost.
Step 1: X’ = T’. Find t Ɛ X’ such that │cov(t)│≥ │cov(u)│for all u Ɛ X’, u ≠ t.
Step 2: Set PrT =
Step 3: Repeat the following steps while X’ ≠ Φ and entityCov ≠ Φ.
-
3.1. Compute the residual coverage for each test t Ɛ T’. resCov(t) = │entitiesCov \ (cov(t) ∩entitiesCov│. resCov(t) indicates the count of currently uncovered entities that will remain uncovered after having executed P against t.
-
3.2. Find test t Ɛ X’ such that resCov(t) ≤ resCov(u), for all u Ɛ X’, u ≠ t. If two or more such tests exist then first compare │cov(t)│, if there is tie again look for executionTime(t) and linesOfCodeTraced(t) and select the one with high │cov(t)│, linesOfCodeTraced(t) and least executionTime(t).
-
3.3. Update the prioritized sequence, set of tests remaining to be examined, and entities yet to be covered by tests in PrT. PrT = append(PrT, t), X’=X’\{t}, and entitiesCov = entitiesCov\cov(t).
-
3. Statistical Approach for Prioritization of Test Cases for Black Box Testers
Step 4: Append to PrT any remaining tests n X’. All remaining tests have the same residual coverage which equals │entitiesCov│. Hence these tests are tied. Now follow exactly what was done in step3.2. That is when two or more tests tie look for test case with higher value of │cov(t) │and linesOfCodeTraced(t) and least executionTime(t).
End of Algorithm
Readers of this paper are strongly advised to trace the example 9.29 in the text book again in conjunction with the algorithm.
This algorithm needs bit of explanations in plain English as the notations of Mathematics often do not go well with the computer science practitioners. In simple terms we start with the test case which covers maximum entities to begin with. Then we choose the test case which will run the maximum uncovered entities that are not already covered by previously run test case. The second step is repeated till there are no more unique entities to be covered. Of course when we encounter two or more test cases with the same cost, we go ahead with the one which has high entities coverage, high loc trace and least execution time. Once all the entities are covered, we choose to run the remaining test cases with the same criteria i.e. high entities coverage, high loc trace and least execution time. The logic behind this is, always choose the test case which covers maximum entities, traces maximum lines of code in least amount of time.
In the introduction section we mentioned about same person wearing different hats of developer and tester. This is with a reason. White box testing is by or with the help of developer.
Although the approach used in section 2 is nice, it involves the product code dissection at class, function level. Therefore we explain a very simple approach which can be used by regression team for prioritizing the test cases when there is no sufficient time to understand and implement the algorithm. As we shall explain in section 4, this approach can be implemented with minimal probes in the test case and minimal tweaking of the tool used for gathering the coverage data.
We explain this directly taking the example. Please have look at the table below.
Where Nmi =
Table 1. Table for Calculating the New Metric
|
Test case number |
Number of lines of code in the test case (LOCTesti) |
Number of lines of code traced in the product code(LOCProdi) |
Execution time (Tl) |
New metric (Nmi) |
|
1 |
||||
|
2 |
||||
|
. . |
||||
|
n |
||||
|
Effectiveness of total test suite = ∑ Nmi |
||||
|
Effectiveness of test suite per test case = |
∑ |
|||
LOCProd
(LOCTest X ᴛ )
The logic needs bit of explanation. We are using the logic that the test case which traces maximum lines of product code with least number of lines in itself in least amount of time is efficient. We sum up the numbers Nmi short for New Metric to get the picture at the test suite level.
However this logic assumes there are no redundant test cases in test suite.
-
4. Coverage Tools: Codecover a Case Study
-
5. Process Flow for Collecting Metrics of Choice.
-
6. Advantages of Test Suite Prioritization
The real advantages of spending effort in test suite prioritization can be explained very easily. Imagine a project which maintains 1000+ test cases. Further, depending upon the system, it could take few days to execute the test cases. These kinds of systems are real in wireless telecom sector. Imagine the period of field support where the developers and testers have to quickly give the fixes for field support issues. The product team cannot afford the time required. In such scenarios it is very advantageous to have the ranked test suite where the tester could decide to end the test case after 500+ test cases. The savings could be substantial amount of time.
-
7. Conclusion
Since we have used the terms such as product lines of code traversed and lines of the code in the test case we need a tool to measure the same. The obvious choice is code coverage tools. There are plenty of coverage tools for code coverage [3]. The choice of tool for particular project depends upon various criteria [3]. We had investigated the CodeCover earlier. Its most suited tool for Java projects since it comes with EPL license and most importantly, it is open source software. It is backed by courteous team of developers who support the tools issues. The tool can be extended and tweaked as per the needs of particular project. Although we have other coverage criteria such as combinatorial coverage at researchers disposal today [5, 6], we need to revisit the traditional coverage criteria code coverage often. Although one of our previous papers [4] attempts to prioritize the test suite, the focus in this paper is completely different. The CodeCover gives various metrics such as statement coverage, branch coverage, loop coverage, MC/DC coverage etc at test case level as well as test suite level. There are provisions to call the Application Programmers Interface (APIs) of this tool from outside. The flexibility to call the APIs from external environment can mean a lot to implement the topics explained in this paper.
In further sections we explain how the APIs could be called from test setup to gather the required data and how it can be combined with other parameter of interest viz. execution time.
The CodeCover already supports two languages as diverse as Java and Cobol. This is being mentioned for reason. That is tweaking of the tool is not effort intensive.
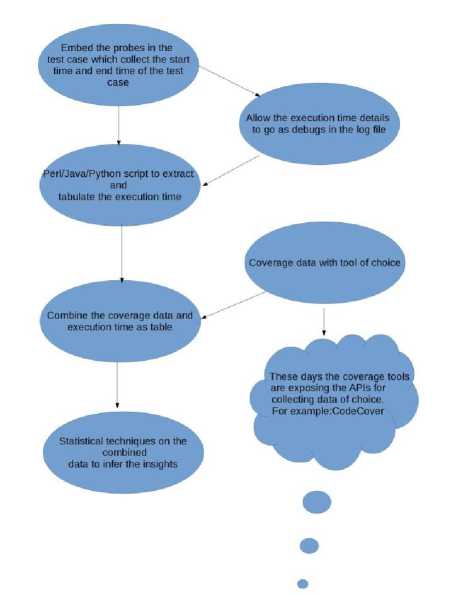
Fig.1. Process Flow for Collecting the Metrics of Choice.
The figure 1 needs bit of explanation. We have been talking about gathering the product code traced and execution time of the test case while collecting the metrics of choice. The figure 1 depicts how this could be done in real life project.
In this paper we presented two approaches mainly for the cases when the testers want to use the black box or white box testing. Each approach is with its own benefits and drawbacks. Either of the approach can be followed depending upon resources and time.
We presented how the metrics being discussed in either of the approaches can be extracted in practical setups. The CodeCover synonymous to Java coverage although incorrect is discussed as case study to explain the fact that the metrics introduced in the algorithm or in the new approach are not difficult to extract.
-
8. Future Work
We will investigate if these concepts can be applied to ongoing commercial project. We shall investigate how the concepts could be improved upon further.
Further we investigate how the concepts explained in this paper can be applied to integrated test environments which we investigated earlier [7].
Acknowledgements
Our sincere thanks to the open source software’s mentioned in the papers without which the practical aspects of the tools usage would not have been possible.
Our sincere thanks to head of the department computer science and information systems who in the capacity of academic council members of the research work being carried out at BITS Pilani, Goa, suggested to look at the problems related to Regression testing. The same was studied and this paper documents the findings.
Our sincere thanks to the authors of the books mentioned in the reference section.
Список литературы Regression Test Suite Prioritization using Residual Test Coverage Algorithm and Statistical Techniques
- Aditya P. Mathur. 2013. Foundations of software testing, 2nd edition text book. University of Purdue.
- Paul C.Jorgensen.2013.Software testing a craftman's approach, 3rd edition, text book.
- Abhinandan H. Patil et al.2013. CodeCover: A Code Coverage Tool for Java Projects, ERCICA Elsevier publications.
- Abhinandan H. Patil et al.2014.CodeCover: Enhancement of CodeCover, ACM SIGSOFT SEN, March 2014 issue.
- Abhinandan H. Patil, Neena Goveas and Krishnan Rangarajan.2015. Test Suite Design Methodology using Combinatorial Approach for Internet of Things Operating Systems, Scientific Research Publishing, Journal of Software Engineering and Application.
- Abhinandan H. Patil, Neena Goveas and Krishnan Rangarajan.2015. Re-architecture of Contiki and Cooja Regression Test Suites using Combinatorial Testing Approach, ACM SIGSOFT SEN, June 2015 issue.
- Abhinandan H. Patil, Preeti Satish, Neena Goveas and Krishnan Rangarajan.2015. Integrated Test Environment for Combinatorial Testing. IEEE conferences, IACC.
- CodeCover Home Page=http://codecover.org/.
- S. Elbaum, A. G. Malishevsky and G. Rothermel. Test case prioritization: A family of empirical studies. IEEE Trans.
- M. J. Harrold, J. A. Jones, T. Li, D. Liang, A. Orso, M. Pennings, S. Sinha, S. A. Spoon and A. Gujarathi. Regression test selection for java software. In OOPSLA '01: Proceedings of the 16th ACM SIGPLAN conference on Object Oriented Programming, Systems, Languages, and Applications, pages 312–326, New York, NY, USA, ACM Press 2001.
- J. A. Jones and M. J. Harrold. Test-suite reduction and prioritization for modified condition/decision coverage. IEEE Trans.Softw. Eng. 2003.
- M. Lyu, J. Horgan and S. London. A coverage analysis tool for the effectiveness of software testing. IEEE Trans. on Reliability 1994.
- G. Rothermel, M. J. Harrold, J. Ostrin and C. Hong. An empirical study of the effects of minimization on the fault detection capabilities of test suites. In ICSM '98: Proceedings of the International Conference on Software Maintenance, Washington, DC, USA, IEEE Computer Society, 1998.
- A. Srivastava and J. Thiagarajan. Effectively prioritizing tests in development environment. In ISSTA '02: Proceedings of the 2002 ACM SIGSOFT International Symposium on Software Testing and Analysis, pages 97–106, New York, NY, USA, ACM Press, 2002.
- T.W.Williams and M. R.Mercer. Code Coverage, what does it mean in terms of quality. IEEE Conference Publications 2001.
- K. Sakamoto and H.Washizaki. Open Code Coverage Framework: A Consistent and Flexible Framework for Measuring Test Coverage Supporting Multiple Programming Languages. IEEE Conference Publications 2010.
- Y. Adler and N. Behar. Code Coverage Analysis in Practice for Large Systems. IEEE Conference Publications 2011.
- F. Del Frate and P. Grag. On the correlation between code coverage and software reliability. IEEE Conference Publications 1995.
- S. Berner and R. Weber. Enhancing Software Testing by Judicious Use of Code Coverage Information. IEEE Conference Publications 2007.
- J. Lawrence and S. Clarke. How well do professional developers test with code coverage visualizations? An empirical study. IEEE Conference Publications.
- W. E. Wong and Yu Qi. Effective Fault Localization using Code Coverage. IEEE Conference Publications 2007.
- R. M. Karcich and R. Skibbe. On software reliability and code coverage. IEEE Conference Publications 1996.
- Zheng Li, Mark Harman and Robert M. Hierons.2007. Search Algorithms for Regression Test Case Prioritization, IEEE transactions on Software Engineering.
- Siavash Mirarab, Soroush Akhlaglv and Ladan Tahvildari.2012. Size Constrained Regression Test Case Selection using Multicriteria Optmization, IEEE transactions on Software Engineering.
- Luay Tahat, Bogdan Korel, Mark Harman and Hasan Ural.2011.Regression Test Suite Prioritization using System Models. Wiley online Library.


