Регрессионная модель диагностики патологий молочных желез по данным микроволновой радиотермометрии

DOI:

Работа выполнена в рамках направления, занимающегося разработкой методов и алгоритмов искусственного интеллекта, предназначенных для анализа и интерпретации медицинских данных, получаемых с помощью микроволновой радиотермометрии, и созданием на их основе технологии разработки экспертных диагностических систем.

Активно развивающийся в последние годы метод медицинской диагностики по данным микроволновой радиотермометрии, основан на измерении собственного электромагнитного излучения внутренних тканей пациента в диапазоне сверхвысоких частот. Изменение температуры тканей, как правило, предшествует структурным изменениям, которые далеко не всегда обнаруживаются традиционными методами диагностики, особенно на ранней стадии заболевания. Например, температурные аномалии могут быть вызваны усиленным метаболизмом раковых клеток, что послужило основой для использования метода микроволновой радиотермометрии в диагностике рака молочной железы. В настоящее время микроволновую радиотермометрию для диагностических целей применяют в маммологии, онкологии, флебологии, гинекологии, хирургии и многих других областях медицины.

Проблема заключается в том, что хотя получаемые температурные данные носят объективный характер, постановка диагноза на их основе остается искусством врача, в том числе – существенно зависит от его специализации, опыта и т. п. Сложность восприятия информации, возникающая у медицинского персонала без специальной длительной подготовки, значительно снижает потенциальную возможность использования термометрической аппаратуры в скрининге. Данное обстоятельство серьезно сужает область применения и, по сути дела, нивелирует уникальные возможности термометрии в ранней диагностике. В том числе причиной последнего является то, что существующие диагностические комплексы не содержат эффективных экспертных систем, не опираются на интеллектуальный анализ и математические модели интерпретации данных и разрабатываются без использования алгоритмов искусственного интеллекта.

В целом данную проблему можно решить созданием интеллектуальных диагностических систем. Интеллектуальными их принято называть в связи с тем, что в них предусмотрен механизм обоснования предлагаемых решений [4], использующий множество специальных знаний из предметной области.

На первом этапе построения экспертной системы диагностики по данным микроволновой радиотермометрии были построены соответствующие математические модели классификации заболеваний вен нижних конечностей. Вначале применялись традиционные методы распознавания состояний на основе статистической обработки данных: нейронные сети (см., например, [1]), байесовский классификатор (см., например, [3; 8]) и т. п. Однако, несмотря на приемлемую точность работы классификаторов, обосновать и объяснить предлагаемые диагностические решения система не могла.

При построении интеллектуальных диагностических систем особую сложность вызывает нахождение высокоинформативных признаков заболеваний. Так как метод микроволновой радиотермометрии находится на начальном этапе развития и применяется в довольно ограниченном числе научно-медицинских центров, количество квалифицированных экспертов крайне мало. В связи с этим многие традиционные методы получения диагностических признаков, основанные на обработке экспертной информации, оказываются малоэффективными. Однако подход, основанный на математической формализации качественных медицинских признаков, построении и анализе соответствующих числовых функций, уже показал свою эффективность (см., например, [6; 7]).

Остановимся подробнее на способе формирования пространства информационных признаков при диагностике заболеваний молочной железы. В основе получения его элементов будет лежать количественное описание качественных медицинских признаков. Вначале опишем подробнее существующую методику диагностики рака молочной железы по данным микроволновой радиотермометрии (см., например, [2]). Применяемый в настоящее время комплекс РТМ-01-РЭС позволяет оценивать функциональное состояние тканей путем измерения внутренней температуры (РТМ) на глубине до 5 см и температуры кожи (ИК). Обследование пациентки проводится в горизонтальном положении, обнаженной по пояс, руки под головой. Обследование начиналось с измерения температур в опорных точках T 1 и T 2, расположенных: первая – в центре грудной клетки сразу под и между молочными железами; вторая – непосредственно под мечевидным отростком. Далее измерения проводятся в 10 точках на каждой железе и в аксилярной области (схема представлена на рис. 1).

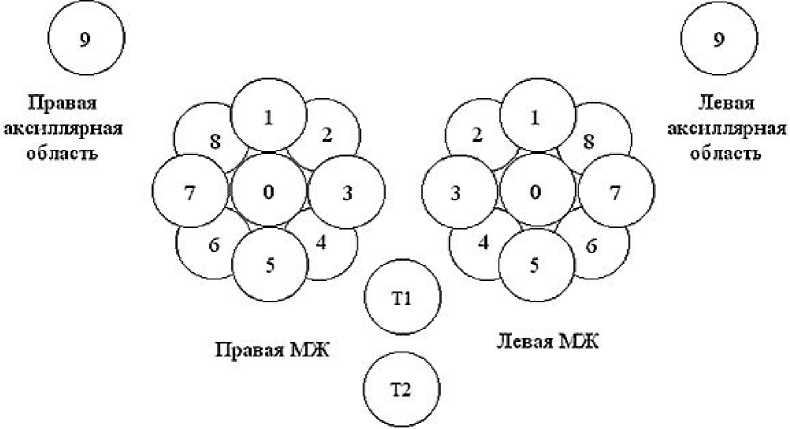
Рис. 1. Схема обследования молочных желез

Обучающая выборка создана на основе базы термометрических данных пациенток, полученной в результате исследований, проводимых в нескольких крупных онкологических центрах России в течение последних нескольких лет. В процессе исследования происходит постоянное пополнение и уточнение базы данных и, соответственно, обучающей выборки. На момент написания данной статьи обучающая выборка включала в себя информацию о 598 молочных железах пациенток в возрасте от 17 до 88 лет (подробнее см.: [5]). Выборка разделена на два контрольных класса: данные термометрических измерений молочных желез здоровых пациенток (122 молочные железы) и данные термометрических измерений молочных желез больных пациенток (476 молочных желез). Последние делятся на следующие классы:

– данные здоровых молочных желез больных пациенток (124 молочные железы);

– данные больных молочных желез больных пациенток (140 молочных желез) и данные пациенток группы «риска» (212 молочных желез).

Отметим, что при интеллектуальном анализе данных микроволной радиотермометрии следует учитывать зависимость результатов измерений от внешних условий и физиологическо- го состояния пациента (см., например, [1; 5]). В соответствие с методикой, измерения проводились при температуре окружающей среды от 20 до 27 градусов. Однако температура окружающей среды при создании обучающей выборки, к сожалению, не фиксировалась. Заметим, что зависимость результатов термометрических измерений от температуры окружающей среды – достаточно очевидна, должна использоваться при анализе данных (см., например, [1]), и после проведения соответствующих исследований, очевидно, будет применяться при анализе данных в диагностике заболеваний молочных желез. Для косвенного анализа влияния температуры окружающей среды было решено использовать температуры в контрольных точках Т1 и Т2. Были исследованы зависимости температур в 9 точках молочной железы от Т1 и Т2 и вычислены соответствующие коэффициенты корреляции (табл. 1). Их анализ показал [5], что температура в контрольных точках имеет высокую степень прямой корреляции с изменениями температуры в молочной железе.

Таблица 1

Коэффициенты корреляции поверхностных и глубоких температур молочных желез пациенток в зависимости от Т1 и Т2

		0	1	2	3	4	5	6	7	8
Т 1, RTM	РТМ	0,60	0,68	0,64	0,64	0,68	0,71	0,69	0,71	0,72
	ИК	0,39	0,56	0,53	0,53	0,59	0,53	0,58	0,56	0,56
Т 2, RTM	РТМ	0,74	0,81	0,75	0,74	0,76	0,77	0,81	0,83	0,81
	ИК	0,54	0,72	0,67	0,60	0,71	0,64	0,70	0,69	0,68
Т 1, ИК	РТМ	0,64	0,55	0,62	0,72	0,73	0,71	0,68	0,66	0,60
	ИК	0,71	0,80	0,78	0,77	0,86	0,83	0,80	0,76	0,76
Т 2, ИК	РТМ	0,63	0,57	0,60	0,68	0,72	0,72	0,70	0,69	0,65
	ИК	0,70	0,81	0,76	0,74	0,84	0,83	0,82	0,73	0,74

Таким образом, естественно возникает идея попытки предобработки данных обучающей выборки с помощью линейной интерполяции зависимости температур в точках молочной железы от температуры в опорных точках и приведения всех температур к одинаковой температуре в опорной точке.

• 1.    Алгоритм

• 2.    Полученные результаты

В качестве примера рассмотрим исследование зависимости t 1 от T 1.

Рассматриваем множество точек ( T 1 i , t 1 i ), i = 1,… , n. Здесь T 1 i и t 1 i – температуры соответственно в опорной точке Т 1 и в точке 1 i -й молочной железы; n – количество молочных желез в обучающей выборке. Методом наименьших квадратов ищем прямую t 1 = a * T 1 + b , наименее удаленную от точек нашего множества. Вычисляем среднее значение T 1 ср и передвигаем наши точки параллельно линии регрессии на прямую T 1 = T 1 ср . В обучающей выборке заменяем ( T 1 i , t 1 i ) на ( T 1 ср , t 1 iн ), где t 1 iн = t 1 i + a * ( T 1 ср – T 1 i ).

Вместо T 1 можно использовать опорную точку T 2, а вместо t 1 – температуру в любой точке молочной железы, а также функцию от нескольких температур, описывающую диагностические признаки. Регрессию можно проводить в ИК и в РТМ-диапазоне.

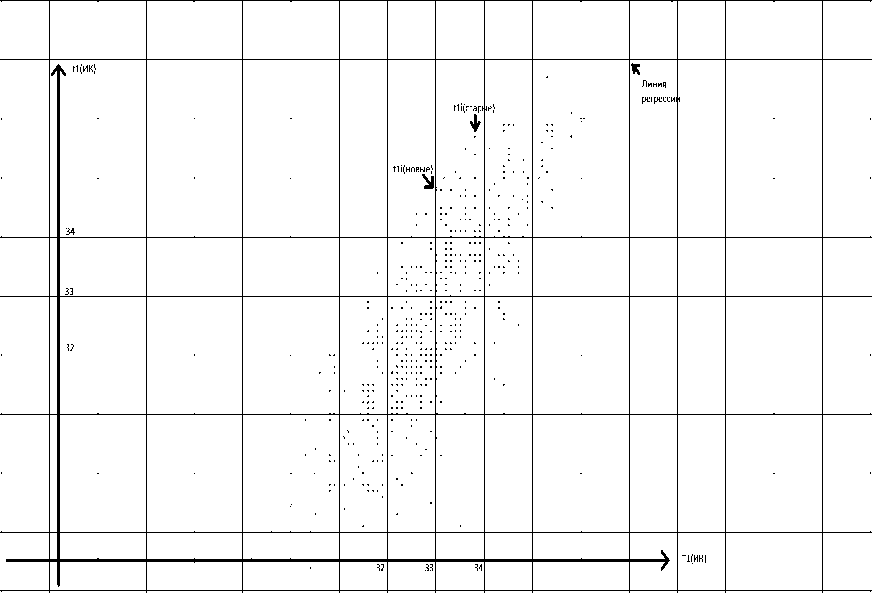
Рис. 2. Иллюстрация алгоритма

Было написано приложение на языке C#, которое реализует описанный выше алгоритм. Пользователь задает опорную точку, после чего программа осуществляет линейную регрессию, вычисляет соответствующие коэффициенты корреляции и изменяет обучающую выборку.

Как указывалось выше, при создании экспертных диагностических систем существенное значение имеют выявление и анализ числовых функций, описывающих качественные признаки (см., например, [1; 6; 7]). Очевидно, что таких функций существует достаточно много. Приведем некоторые примеры.

• 1.    Повышенная величина термоасимметрии между одноименными точками молочных желез. В качестве функции, которая описывает данный эффект, можно использовать, например, | t_np .i - t^ i |, где t_np .i и t_л . _i - температуры в i - х точках правой и левой молочных желез соответственно.

• 2.    Повышенная температура соска в пораженной молочной железе по сравнению со средней температурой молочной железы. В качестве функции, которая описывает данный эффект, можно использовать t 0 – t ср.

• 3.    Повышенная дисперсия разности температур между железами. В качестве функции, которая описывает данный эффект, можно использовать, например, ∑ ⁸₀( ∆ t_i – t _мж)², где D t i = t пр.i – t л.i ,

• 4.    Повышенное значение температуры соска по сравнению с каждой точкой молочной железы. В качестве соответствующих функций можно использовать, например, t 0 – t i . Аналогично можно использовать ряд функций, описывающих сравнение температуры соска со средней температурой различных областей молочной железы. Например, повышенное значение температуры соска по сравнению со средними значениями соседних точек молочной железы можно описать функциями t 0 – ( t i + t i +1 ) / 2.

8 ∆t t = i.

мж ₀ 9 .

Вообще, при исследованиях было проанализировано несколько сотен числовых функций, которые характеризовали степень симметрии температурных полей, наличие зон аномально высокой или низкой температуры и другие качественные медицинские диагностические признаки.

Перейдем к точным определениям информативных признаков. Пусть t^i = 0,... ,9 - температура i -й точки j -й молочной железы; t i ₀ = Т^, t^ = Т ₂ - температуры опорных точек j -й молочной железы, измеренные в РТМ-диапазоне. Аналогично, пусть t / , i = 12, ... ,21 - температура i -й точки j -й молочной железы; t 2 ₂ = Т^, t ^/ ₃ = Т ₂ - температуры опорных точек j -й молочной железы, измеренные в ИК-диапазоне. Тогда обучающую выборку можно представить в виде матрицы

/ to — t23 \

^  -  tg3

t fc+1 ... ffc+1

tO

””

\ to где t/ при j = 1, ..., к - температуры молочных желез здоровых пациенток; t/ при j = к + 1,... ,п - температуры молочных желез больных пациенток.

Пусть f^q - q -я исследуемая функция, определенная на множестве векторов:

Q _q = {(t 0 , ^,t ^/ ₄ )},гдеj = 1, _,п. Обозначим f ^q = f ^q (t 0 , .^,t 2 ₃ ). В работе исследуются всевозможные пары (f ^q ,X), где X - подобласти множества Q _q . Характеристический признак считается выполненным, если f ^q 6 Q _q \X для некоторых j = к + 1,..., n и f ^q 6 X для всех j = 1, ..., k .

Таким образом, поиск характеристических признаков заключался в нахождении подобластей, на которых множество значений функций f ^q , соответствующих множеству векторов (t 0 , - , t 2' ₃ ) приj = 1,...,к, будет пустым. Из этих подобластей выбирается подобласть, содержащая множество значений функций f ^q , которому соответствует наибольшее количество векторов (t 0 , - , t 2' ₃ ) приj = к + 1, _,п.

Однако множество больных пациенток, у которых выполнен хотя бы один из характеристических признаков, оказалось, как и ожидалось, недостаточно широкими – примерно 60 %. Применение существующих логических алгоритмов классификации предполагает использование достаточно широкого набора высокоинформативных признаков. Для оценки каждого признака были использованы величины, которые традиционно относят к информативностям.

В качестве оценки использовались:

– статистическая информативность:

i ? =

-ln

/CSC6A

\ р т+к г XСМ+К/ где M – количество молочных желез класса «Здоровые»; m – количество молочных желез класса «Здоровые», у которых выполнен признак; K – количество молочных желез класса «Больные»; k – количество молочных желез класса «Больные», у которых выполнен признак;

– эвристическая информативность:

q   maX {%,у}

b[ =             ,

1 min {%, у} где x – доля молочных желез класса «Здоровые», у которых выполнен признак; y – доля молочных желез класса «Больные», у которых выполнен признак;

– комбинированная информативность:

c f = /F^.

Использование в алгоритмах классификации среднего геометрического значения статистической и эвристической информативностей обусловлено рядом причин. А именно: статистическая информативность отделяет достаточно большие группы исследуемых объектов, но при этом теряется точность, эвристическая же информативность достаточно точная, но при этом отделяет маленькое количество исследуемых объектов.

С помощью приложения, осуществляющего предобработку данных с помощью линейной регрессии, – изменялась обучающая выборка, пересчитывались все температуры с целью улучшения параметров отдельных признаков алгоритма диагностики.

В качестве основного параметра, характеризующего эффективность высокоинформативного признака, будем использовать комбинированную информативность. После регрессии по T 1 и по Т 2 у большинства признаков наблюдается увеличение комбинированной информативности (табл. 2).

Таблица 2

Пример признаков, у которых увеличилась информативность

Функция признака	До	После
to—(t^	8,8	10,5
(t6 +1-) t ср        2	6,6	6,8
t6, ртм — t6, ик	3,4	5,0
t ср — t3	4,0	5,0

У характеристических признаков показателем эффективности служит доля больных, которую обнаруживает данный признак. После пересчета у большинства признаков эта доля осталась прежней, хотя несколько характеристических признаков незначительно повысили свою эффективность. Примером такого признака служит t₀ — 6—7 - . До регрессии данный признак обнаруживал 8 % больных, после регрессии – 9 % больных.

После пересчета обучающей выборки были проведены вычислительные эксперименты для проверки улучшения параметров алгоритма диагностики. Таблица 3 показывает результаты диагностики пациентов только по характеристическим признакам. Налицо небольшое улучшение специфичности и точности.

Таблица 3

Изменение эффективности диагностики по характеристическим признакам

	Исходный алгоритм		После регрессии по Т 1		После регрессии по Т 2
	МЖ	Пациентки	МЖ	Пациентки	МЖ	Пациентки
Точность	69,4	72,24	73,41	76,59	73,58	77,93
Чувствительность	61,55	65,13	66,6	70,59	66,81	72,27
Специфичность	100	100	100	100	100	100

Таблица 4 демонстрирует улучшение параметров алгоритма диагностики с использованием и характеристических, и высокоинформативных признаков. После регрессии по Т 2 эффективность алгоритма возрастает примерно на 4 %.

Таблица 4

Изменение эффективности диагностики по всем признакам

	Исходный алгоритм		После регрессии по Т 1		После регрессии по Т 2
	МЖ	Пациентки	МЖ	Пациентки	МЖ	Пациентки
Точность	75,59	77,93	79,43	81,27	79,93	84,28
Чувствительность	70,59	73,95	74,79	77,31	76,47	82,77
Специфичность	95,08	93,44	97,54	96,72	93,44	90,16

Также в работе была предпринята попытка использования нелинейных моделей регрессии, у которых можно сделать линеаризующее преобразование. Для получения новых обучающих выборок использовалась гиперболическая, логарифмическая, степенная, показательная и экспоненциальная регрессия (см. рис. 3 и 4).

Как можно видеть из рисунков 3 и 4, внутри диапазона, в котором находятся температуры пациентов, линии регрессии становятся идентичными с точностью 0,1o.

Вследствие этого применение таких регрессий не дает существенного изменения обучающей выборки по сравнению с линейной регрессией.

40.000000
30.025000			///
20.050000
10.075000	6.750000	13.400000	20.050000	26.700000	33.350000

Рис. 3. Линии регрессий между t 1 и T 1 в РТМ-диапазоне

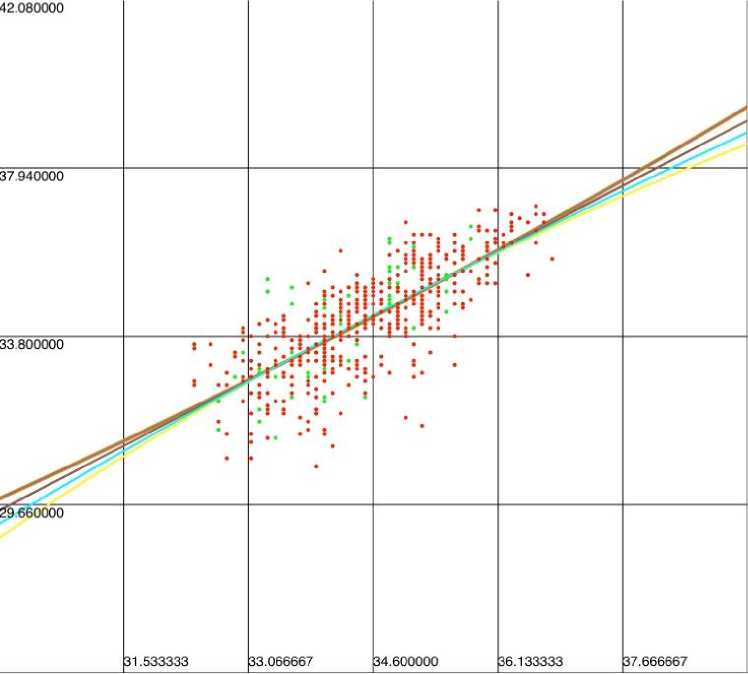
Рис. 4. Линии регрессий между t 1 и T 1 в РТМ-диапазоне