Регулирование угловой скорости шагового двигателя

Введение. Шаговые электродвигатели применяются в приводах машин и механизмов, работающих в старт-стопном режиме или в приводах непрерывного движения, где управляющее воздействие задается последовательностью электрических импульсов, например, в манипуляторах. В отличие от сервоприводов шаговые приводы позволяют получать точное позиционирование без использования обратной связи от датчиков углового положения. Регулирование угловой скорости шагового двигателя по цепи якоря позволяет определить параметры переходных процессов работы шагового двигателя, а также получить качественную картину фазового портрета, зависящего от вида исходной характеристики нелинейности системы.

Цель исследования: изучение процесса регулирования угловой скорости шагового двигателя по цепи якоря.

Объект, методы и результаты исследования . Объектом исследований выбран шаговый двигатель манипулятора (рис. 1).

Гибридный двигатель объединяет преимущества первых двух типов двигателей: малый шаг поворота и большой момент. Это двигатель с постоянными магнитами, но с большим количеством полюсов. Количество шагов на оборот пропорционально количеству фаз статора и количеству полюсов (зубцов) ротора. Наиболее распространены шаговые двигатели с числом шагов на оборот от 100 до 500 (3,6– 0,72° на один шаг) [1].

Для исследования динамики шагового двигателя выполнено математическое моделирование процесса регулирования угловой скорости по цепи якоря двигателя в MATLAB*SIMULINK.

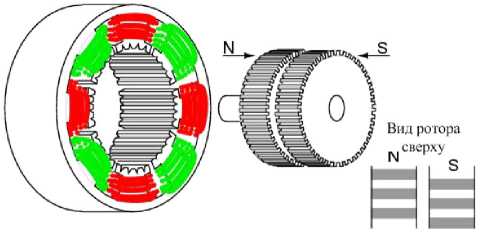
Рис. 1. Конструкция гибридного двигателя

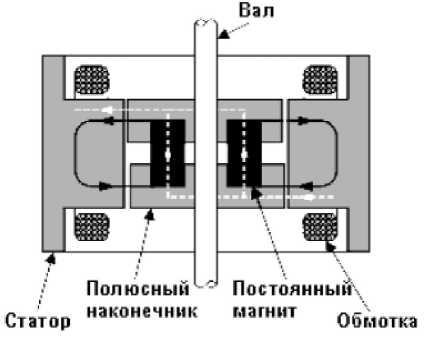
Математическая модель процесса регулирования угловой скорости по цепи якоря приведена в виде уравнений якорной цепи двигателя, движущего момента для вращательного движения, а также приведенную массу [2].

di

U=R^ + L -- -z aLsi , s dt     p    s q di

-— ^- z p ^{a L}s i_q ⁺ z_P ^a^o , s dt

d

sd

U = R_si_d + L qs

T da

I— = M - M_r, dt               ^{c ,}

^M =2 z p ^ o i q ,

^M с = ^Rm Иа ^{1 + f (} mXg ^{+ 2} mg^

2( 1 1⁺ 1^ )

m = тл +2 m ~ +--1 дв , пр 1    2    R 2

валу двигателя; R – радиус колес; m 1 – масса тележки; m 2 – масса колес; a – ускорение.

В качестве допущения принято: влияние про-тиво-ЭДС незначительно. Для настройки регулятора использована операторная форма с обратной по произведению передаточной функции прямой ветви и ветви обратной связи контура регулирования. Инерционность преобразователя невозможно скомпенсировать, поэтому она исключена из синтеза.

Перейдя в операторную форму записи, передаточные функции для контура тока выглядят так:

W nP ( p ) =

K        1/ R я

-------------------------------------.-----------------------------------

(T mn ■ P + 1) (Т я ■ P + 1)

W oc ( P ) = K dm ■

где U _d – напряжение двигателя; R _s – сопротивление двигателя; i_d – сила тока двигателя; L – индуктивность обмотки возбуждения; z – приведенное сопротивление; i – сила тока якоря; U_q - напряжение якоря; a - угловая скорость; p₀ - угол сдвига фаз; M - нагрузочный момент; M_c – момент сопротивления; m пр – приведенная масса манипулятора; f – коэффициент трения качения колес; I 1 – момент инерции колеса относительно его оси; I дв – момент инерции двигателя; М с – требуемый момент на

Так как в контуре тока присутствует возмущение, то регулятор тока принят ПИ типа. Умножив полученную передаточную функцию на интегратор с постоянной времени T т , получим искомую передаточную функцию:

W pt ( P ) =

(Т я ■ p + 1) ■ R я ,

К _S m ■ K mn • T m ' P ’

Передаточная функция всего контура тока:

W KPT ^{( p} )

1/ К d m

T_mnT_m ■ p² + T m ■ p + 1’

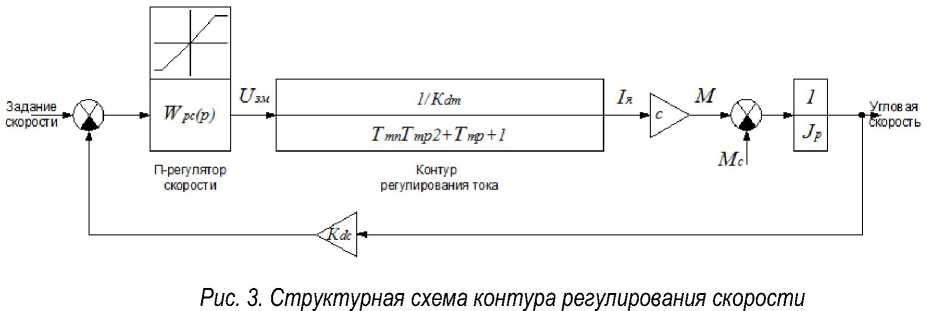
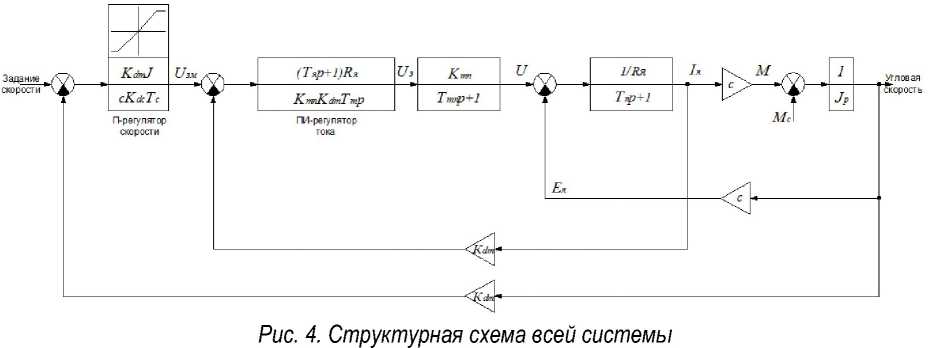
Аналогично выполняется настройка контура регулирования скорости. В итоге получаем передаточную функцию регулятора скорости и структурную схему всей системы целиком [4]:

W PC ( p ) = ^m^ ;

c ⋅ К _{∂ c}T_c

Структурная схема контура регулирования тока приведена на рисунке 2.

Структурная схема контура регулирования скорости приведена на рисунке 3.

На рисунке 4 приведена структурная схема всей системы.

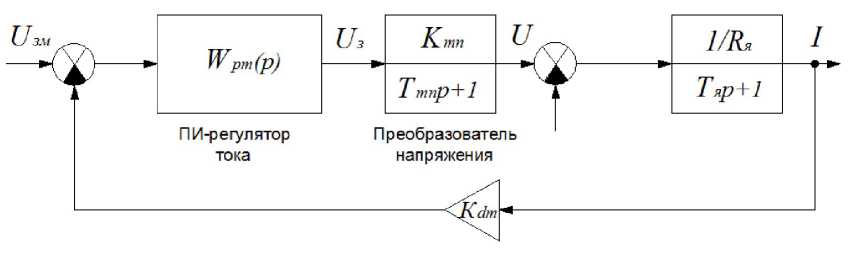
Рис. 2. Структурная схема контура регулирования тока

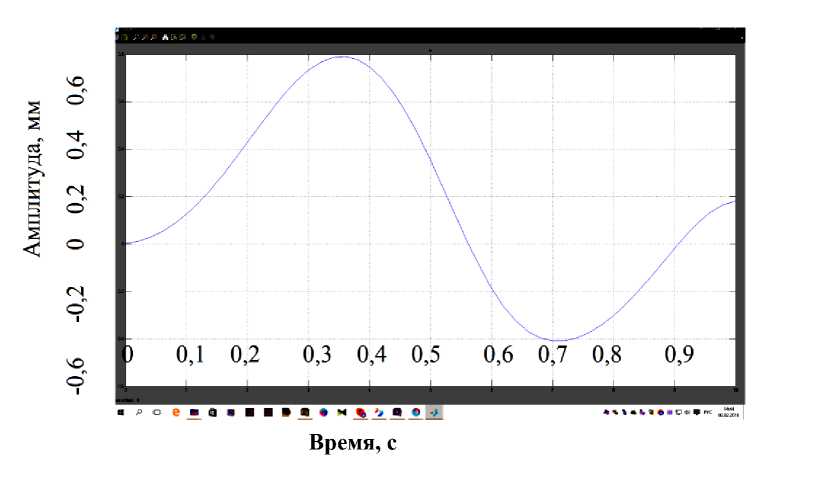
Реализация математической модели приведена на рисунке 5. Переходные процессы работы шагового двигателя носят колебательный характер.Форма колебаний отлична от синусоидальной, и их различие тем больше, чем больше амплитуда колебаний. В силу специфики нелинейных свойств амплитуда колебаний привода растет быстрее, чем амплитуда тока. Так как в контуре тока присутствует возмущение, а его необходимо выполнить астатическим, следовательно, регулятор тока принимается типа ПИД регулятора.

Для построения фазового портрета для модели серводвигателя использовался узел дифференцирования (du/dt) и узел отображения информации по двум координатам (XY Graph) [5].

Время, с

0,1 0,2    0,3 0,4 0,5    0,6 0,7 0,8    0,9

Рис. 5. Переходные процессы работы серводвигателя

Качественная картина фазового пространства исследуемой системы привода манипулятора определяется корнями λ характеристического уравнения. На рисунке 6 приведен полученный узел отображения информации по двум координатам в виде фазового портрета привода

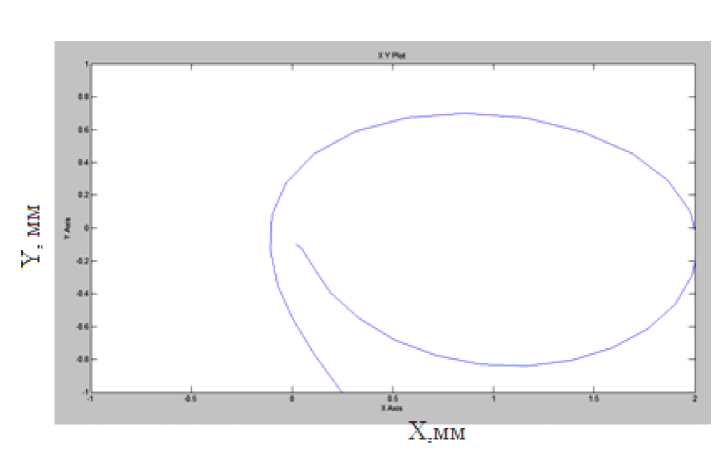
Рис. 6. Узел отображения информации по двум координатам

Заключение:

– математическая модель шагового двигателя позволяет моделировать переходные процессы, связанные с изменением угловой скорости шагового двигателя по цепи якоря;

с шаговыми двигателями. Отображения информации по двум координатам составили: по оси X – 0,8 мм и оси Y – 2,0 мм. Исследования модели серводвигателя показали, что эта система является устойчивой.

– результаты моделирования динамических процессов шагового двигателя установили качественную картину фазового портрета привода манипулятора и степень устойчивости системы по критерию Найквиста.