Регуляризация решения нелинейного интегрального уравнения первого рода
Автор: Чоюбеков С.М., Чоюбекова А.М.
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Физико-математические науки
Статья в выпуске: 12 т.9, 2023 года.
Бесплатный доступ
Интегральные уравнения, основной раздел математики, широко используются в физике, технике, механике, теории управления и других областях. Связанные с применением интегральных уравнений, развиваются новые области, такие как экономические науки, некоторые разделы биологии и т. д. Теория интегральных уравнений в основном развивалась в конце девятнадцатого - начале двадцатого века, начиная с Вито Вольтерры (1982, 1986), Эрика Ивара Фредгольма (2010), Давида Гильберта, Эрхарда Шмидта и т. д. ее начали изучать ученые. Тем не менее, в рамках математических концепций, существовавших до первой половины двадцатого века, такие задачи считались некорректными из-за того, что небольшое изменение заданных функций приводило к большему изменению искомых функций. Уравнение Вольтерра первого рода - это интегральное уравнение, которое имеет точное решение только в некоторых случаях. Предел интеграции был проведен в очень небольших количествах по неклассическим линейным и нелинейным интегральным уравнениям с переменными пределами и построение решений в этих работах основано на численных методах. Поэтому для так называемых неклассических интегральных уравнений Вольтерра актуальным является определение условий, обеспечивающих единственность и регуляризацию их решений. В рассматриваемой работе разрешено решение единственности неклассического нелинейного интегрального уравнения Вольтерра первого рода. Целью исследования является решение неклассического интегрального уравнения Вольтерра первого рода, то есть определение условий, обеспечивающих единственность решения нелинейного неклассического интегрального уравнения Вольтерра первого рода. Предложенные методы можно использовать для исследования интегральных, интегро-дифференциальных уравнений типа интегрального уравнения Вольтерра первого рода, а также при качественном исследовании некоторых прикладных процессов в области физики, экологии, медицины, геофизики, теории управления сложными системами.
Интегральные уравнения, искомая функция, единственность, переменные
Короткий адрес: https://sciup.org/14129290
IDR: 14129290 | УДК: 517.983 | DOI: 10.33619/2414-2948/97/03
Текст научной статьи Регуляризация решения нелинейного интегрального уравнения первого рода
Бюллетень науки и практики / Bulletin of Science and Practice
УДК 517.983
Теоретическая часть интегральных уравнений изучалась и исследовалась во многих различных работах. В частности, в работе [1] рассмотрен о полилинейных уравнениях Вольтерра 1 рода. В работе [2, 3] изучаются «О единственности решения операторных уравнений Вольтерра» и «Регуляризация и единственность решений уравнений Вольтерра первого рода».
В работах [4–10] исследованы об решение интегральных уравнений Вольтерра первого рода. В работах [11–14] построен регуляризирующий оператор для решения неклассического интегрального уравнения с условиями Липшица и доказаны теоремы единственности.
В данной работе представлено решение неклассического нелинейного линейного интегрального уравнения Вольтерра первого рода.
Постановка задачи
Рассмотрим
t
J K ( t , s , u ( s )) ds = f ( t ); t g [ t 0, T ] a ( t )
где a(t) g С[10,T] , a(10) = 10 , a(t) < t , f (t) - на отрезке [10, T] и K(t,s,u(s)) - в области G = {(t, s): 10 < t < T, a(t) < s < t} (t < t а(т) < a(t)) заданные функции. u(t) - искомая функция на отрезке [t0, T]. Требуем выполнения следующих условий:
1 0 a ( t ) g С 1 [ 1 0, T ], a (t ) > 0 при почти всех t g [ 10,T ] ;
2 0 При фиксированным t g [ t0 , T ] , K o ( t , s ) g L [ a ( t ), T ] и K o ( t , t ) > m > 0 при почти всех t g [ 1 0 , T ] ;
|(cc ) © I
3 0 V t , т , ( t > т ) при всех ( t , s ), ( т , s ) е G , | ^ 0 ( t, т ) - K o ( s, т )| < L0\t - s |, L 0 > 0 - const .
4 0 При всех ( t, т ,и ) , ( s , т , u ) , ( t , т , u2 ) и ( s, т ,u2 ) е G x R ,
|K(t, т ,u2) — K ( s, т ,u2) — K(t, т ,u ) + K ( s, т ,и )| < L|t — s\u — u2 1, L > 0 — const . K ( t , t , и ) = 0
и K 1 ( a 1 ( t ), t , u ) = 0 , при V ( t , u ) е [ 1 0, T ] x R , K ( t , s ,0) = 0 при V ( t , s ) е G
Решение:
Пусть K ( t , s , u ( s )) = K ( t , s ) u ( s ) + K ( t , s , u ( s )) Тогда уравнение (1) можно представить
tt
J K ( t , s ) u ( s ) ds + j K ( t , s , u ( s )) ds = f ( t ); t е [ t 0, T ]
a ( t ) a ( t )
Наряду с уравнением (2) рассмотрим tt
8 v ( t , 8 ) + j K o ( t , s ) v ( s , г ) ds + j K ( t , s , v ( s , 8 )) ds = f ( t ) + 8 u ( t 0) ; t е [ t 0, T ] a ( t ) a ( t )
0 < 8 < 1 некоторый малый параметр. Его решение будем искать в виде
v ( t , 8 ) = u ( t ) + ^ ( t , 8 ) ; (4)
где u(t)- решение уравнения (2), а { (t, s')- неизвестная функция.
Подставив решение (4) в уравнение (3) и выполнив ряд преобразований [11–14], получим следующее уравнение:
1 t j K 0 ( s , s ) ds
H 0( t , т , 8 ) = -K 0( a ч( т ), т ) e 8 a — 1( т ’ ε
1 — - j K 0 ( s , s ) ds 1 — 8 J K 0 ( s , s ) ds (7)
H 1 ( t, т , 8 ) = — e 8 т [ K 0 ( t, т ) — K 0 ( т , т ) ] + e a ( ' ) [ K 0 ( t , т ) — K 0 ( a ‘( т ), т ) ] —
εε
1 a ) — 1 j K 0 ( т , т ) d т
2 K 0 ( s , s ) e 8 [ K 0 ( t , т ) — K 0 ( s , т ) ] ds ;
ε τ
Бюллетень науки и практики / Bulletin of Science and Practice Т. 9. №12. 2023
1' 1 ‘.
1 - J K o ( s , s ) ds 1 I - J K o ( t , t ) d T
H 2( t , t , £ ) = - e £ t [ K o ( t , t ) - K o ( T , T ) ] - K o ( s , s ) e £ s [ K o ( t , t ) - K o ( s , t
££
τ
-1 JK o( s, s) ds
N o ( t , t , u ( t ), £ ( t , £ ), £ ) = e () [ K 1 ( t , t , u ( t ) + ^ ( t , £ )) - K 1 ( t , t , u ( t ))]
ε
I -1J K 0( s, s) ds(10)
N ( t , T , u ( t ), ^ ( t , £ ), £ ) = - e £ t [ K ( t , T , u ( t ) + ^ ( t , £ )) - K j ( t , T , u ( t )) -
ε
1 a ^T ) - 1 J K o ( T , T ) d
- K ( t , t , u ( t ) + ^ ( t , £ )) + K ( t , t , u ( t ))] - K o( s , s ) e £s [ K ( t , T , u ( t ) + ^ ( t , £ )) -
£
-
- K ( s , t , u ( t ) + ^ ( t , £ )) - K ( t , t , u ( t )) + K ( s , t , u ( t ))] ds ;
1 - 1 J K 0( s , s ) ds (11)
N 2 ( t , T , u ( t ), ^ ( t , £ ), £ ) = - e £ t [ K 1 ( t , T , u ( t ) + ^ ( t , £ )) - K 1 ( t , T , u ( t ) + ^ ( t , £ )) -
ε
1 '.
1 - J K o ( T , T ) d T
- K 1 ( t , t , u ( t )) + K 1 ( t , t , u ( t ))] - K o ( s , s ) e £ s [ K 1 ( t , t , u ( t ) + ^ ( t , £ )) -
£
-
- K ( s , t , u ( t ) + ^ ( t , £ )) - K ( t , t , u ( t )) + K ( s , t , u ( t ))] ds ;
t
- - J K o( s , s ) ds 1 ' - 1 J K o ( T , T ) d
U ( t , £ ) =- [ u ( t ) - u ( t 0)] e ’ 0 - K o ( s , s ) e £ s [ u ( t ) - u ( s )] ds ;
ε ' 0
Далее нам понадобится следующие леммы доказанная в [11-14].
Лемма 1. Если выполняются условия 10-20, тогда для функции H0(t, T, £) определенной по формуле (8) имеет место а (')
J | H o ( ' , T , £ ) d T < Y o ; ' e [ ' 0, T ]
' 0
где Y 0 =
I K 0( v , a ( v ))| a '( v )
SUP 1—1л— v< 10, T ] K 0(v,V )
Лемма 2. Пусть H (t, T,£) и H2 (t, T, £) определены по формулами (9),(10)
соответственно. Кроме того выполняются условия 10 - 30. Тогда справедливы оценки
1) |H1(t, t,£)| m 2) |H2(t, t,£)| < L0, (t, t) e G = {(t, t): 10 < t < T, a(t) < t< t}; m Лемма 3. Пусть выполняется 10-20 и функция U(t, £) (£ > 0) определена формулой (14). Тогда: 1) Если u (t) e С [ 10, T ], то на отрезке [ 10, T ] справедлива оценка IIU(t,£)lIc - 3Iu(t)llce £'~в + ®u(£в)=C°(£); ° < в < i, где ^u (S') = sup \u (t) - u (s)|; t - s| < S 2) Если u(t) e CY[t°,T], ° < /< 1, то на отрезке [t0, T] справедлива оценка IU (t, £)|c< c° C^, где С = sup t, S e[ t °, T ] | U (t) - U ( S )| ‘ - sY ; w Co = Je-mTTY-1dr . ° Лемма 4. Пусть выполняются условия 10,20 и 40 функции N°(t,т,u(т),^(т,£),£) , N(t,T,u(т),^(т,£),£) и N(t,T,u(т),^(т,£),£) определены соответственно формулами (11), (12) и (13). Тогда имеют места следующие неравенства 1) |N°(t,т,u(т),^(т,£),£)| < L'e |^(т,£)|; m 2) N1 (t, т, u(т), ^(т, £), £)| < L- (— + 2e4 +1)|^(т, £)|; mm 3) |N2 (t, т, u(т), ^(т, £), £)| < — ^(т, £)| m Доказательство. Если переходить к оценке в (11), (12) и (13) соответственно с учетом условий леммы, получаем требуемые оценки. 1 -1IK°(т,т)dт IN°(t,т,u(т),^(т,£),£)| = e -(т) K-(t,т,u(т) + ^(т,£)) - £ -K(а-1(т),т,u(т) + ^(т,£)) -K(t,т,u(т)) + K(а~'(т),т,u(т))| < -m(t-а *(т)) < e £ L- (t - а ~ (т))^(т, £)| < sup e“^(т, £)|L- < e|£(т, £)|. £ v >° т а ,(т) +? I т m 1 - (t - т) IN,(t,т,u(т),^(т,£),£)| <-е £ L1(t - т)|^(т,£)| + 1 —IK °(т ,т)dт -11к°(т,т)dт u = t - s, dv = —K (s, s)e £s ds, Ko(s, s)e £s L (t - s)^(т, £)|ds = £ t —K °(т ,т) dт du = - ds, v = e £s < < ^ L, 1 - JK°(т.т)dт < — sup[e mvv] + (t - s)e £s m v >° s L1 -I1t \ а (т) —JK°(т,т)dт + — J Le £s ds< £ т Le-1 m2 + L1 t - а'(т) -m(t-а 1(т)) t - т -m(t-т) -----— e £ +---e £ £ £ + L1 а Чт) £ J m (t-s) , e £ds >|^(т,£)| < < Le 1 / -mv \ L £ /- 7(t-а'(т)) - 7(t-т \ I L e^, e 1 4 | + 2L1sup(e v) + 1 (e £ - e £ )^(т,£) < ^(---+ 2 e + 1)^(т,£) ; m v >° £ m mm IN2(t,t,u(t),^(t,8),8)| < 1e ε x L (t - s)|^(t, 8)|ds< -1 Ko(t,t ) dт ε τ 1 t -1J Ko(t T) dт L1(t- T)|^(T, 8)| + p JK0(s, s)e S x τ 1t 1 —J K o(t ,t dT u = t — s, dv = —Ks (s, s) e 8 s ds, ε du = - ds, — J K о (t ,t ^t v = e εs 1 —1J K o(t ,t ^t 1 —1J K o(t ,t ^t= = e 8t L1(t - t)\^(т, 8) + e 8s L1(t - s)|^(т, 8) ε ε 1 ' —1J Ko(t,t)dr , L, Г — m(t — s) L .. + L e 8s ds^^, 8) < — e 8ds< — ^(t, 8) . εε ττ И так сформулируем основные результаты. Теорема. Пусть выполняются условия 10-40 и в1 = Y0eM(T ‘о)< 1, где Yo = | Kо(и, a(u))|а'(и) sup J------------------- и M = 2L0 (e4 +1) + L1 (— + 3e 1 + 2) . mmm Тогда: 1) Если уравнение (1) имеет решение u(t) в пространстве C[10,T], то решение v(t, 8) уравнения (2) при 8 ^ 0 сходится по норме C[t0, T] к решению u(t) и справедлива оценка eM (T—tо)— ± ||v(t, 8) —u(t)||c< [3|u(t)||c e1—в + wu (8е )] . 1 — в1 где Wu (8е ) = sup |u(t) — u (s)|; t-s ≤εβ 2) Если уравнение (1) имеет решение u(t) в пространстве CY[10,T] , (0 < Y< 1) то решение v(t,8) уравнения (2) при 8 ^ 0 сходится по норме C[tо,T] к решению u(t) и справедлива оценка eM (T—tо) (22) ||v(t,8) —u(t)||c< CоcyY8Y , 1 —A ∞ где Co= J e—m^—1dт, CY = Iu (t) — u (s )| sup 1-------------1 γ t, s€[ t о,T] t — s Доказательство. В силу лемм 1–4 из (7) имеем: a (t) a (t) t I ^( t, 8 )| < J |Ho( t ,t, 8 )| ^(t, 8 )| dт + J \H X t ,t, 8 )| ^(t, 8 )| dт + J \H2( t ,t, 8 )| ^(t, 8 )| dт + t 0 t 0 a ( t ) a (t) a( t) + J No( t ,t, u (t ), ^(t, 8 ), 8 )| dт + J N((t ,t, u (t ), ^(t, 8), 8 )| dт + t 0 t 0 t + JN2(t,t,u(t),^(t,8),8)|dт + \U(t,8)|;t € [tо,T] ; a (t) a (t ) I£(t,£)| < Yo||^T,£)||c + j [—(2e- +1) + —#T£)|dr + Сmm t 0 a(t) ,.p-1 + [ [-1— + -4 — + 2e-+1) + -^«(r,£)dr + U(I,£) t e[t„,T]; m m mm t 0 Отсюда для Vt e[10, T] получим t ||^(t, £)||c < Yo|^(t, £)||c + JM|£T, £)|dт + U(t, £)| t0 где M = 2-0( e1+1) + L4 — + 3e_1+ 2) m mm Применяя к этому неравенству неравенство Гронулла-Бельмана, мы получаем следующее неравенство: ||^t,£)||c< Y0eM(T-t0)|Пt,£)||c + eM(T-0)|U(t,£)||c Из этого следует (23) на основе леммы 3. Теорема доказана. Заключение Поставленная задача полностью разрешена, т. е. решение неклассического нелинейного интегрального уравнения является единственным и построен оператор регуляризации.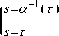
Список литературы Регуляризация решения нелинейного интегрального уравнения первого рода
- Апарцин А. С. О полилинейных уравнениях Вольтерра I рода //Автоматика и телемеханика. 2004. №2. С. 118-125. EDN: NQTYFH
- Асанов А. О единственности решения операторных уравнений Вольтерра // ИзвестияАН Киргизской ССР. 1988. Т. 1. С. 13-18.
- Асанов А. Регуляризация и единственность решений уравнений Вольтерра первого рода: дисс. ... канд. физ.-мат. наук. Новосибирск, 1982. 91 с.
- Бухгейм А. Л. Об одном классе операторных уравнений Вольтерра первого рода // Функциональный анализ и его приложения. 1972. Т. 6. №1. С. 1-9. https://doi.org/10.1007/BF01075502
- Денисов А. М. О приближенном решении уравнения Вольтерра I рода // Журнал вычислительной математики и математической физики. 1975. Т. 15. №4. С. 1053-1056. https://doi.org/10.1016/0041-5553(75)90185-8
- Иманалиев М. И., Асанов А. О решениях систем нелинейных двумерных интегральных уравнений Вольтерра первого рода // Доклады Академии наук. 1991. Т. 317. №1. С. 32-35.
- Иманалиев М. И. Обобщенные решения интегральных уравнений первого рода. Фрунзе: Илим, 1981. 144 с.
- Лаврентьев М. М. Об интегральных уравнениях первого рода // ДАН СССР. 1959. Т. 127. №1. С. 31-33.
- Магницкий Н. А. Линейные интегральные уравнения Вольтерра I и III рода // Журнал вычислительной математики и математической физики. 1979. Т. 19. №4. С. 970-988. https://doi.org/10.1016/0041-5553(79)90166-6
- Цалюк З. Б. Интегральные уравнения Вольтерра // Итоги науки и техники. Серия Математический анализ. 1977. Т. 15. №0. С. 131-198. https://doi.org/10.1007/BF01844490
- Асанов А., Чоюбеков С. М. Регуляризация решения нелинейных уравнений Вольтерра I рода с условиями Липшица // Точная наука. 2018. №23. С. 6-11. UPGRGU
- Асанов А. А., Чоюбеков С. М. Решение неклассических интегральных уравнений Вольтерра I рода с вырожденным нелинейным ядром // Международный научно-исследовательский журнал. 2018. №4 (70). С. 134-138. https://doi.org/10.23670/IRJ.2018.70.029
- Асанов А., Чоюбеков С. М. О решении линейных неклассических интегральных уравнений Вольтерра первого рода // Наука, новые технологии и инновации Кыргызстана. 2020. №1. С. 3-8. https://doi.org/10.26104/NNTIK.2019.45.557
- Чоюбеков С. М. Регуляризация решения неклассического интегрального уравнения со условиями Липшица // Молодой ученый. 2016. №8. С. 34-38. EDN: VWFZHJ


