Регуляризация в обратных динамических задачах для уравнения $SH$ волн в пористой среде

Многие инженерные проблемы сводятся к решению чисто математических задач. Переход от инженерных задач к чисто математическим нередко представляет большие трудности, поэтому создание математических моделей физических процессов — важнейшее направление современной науки. Широкое распространение в задачах механики жидкости и газа получили краевые задачи, т. е. задачи, в которых либо форма объекта (подземного контура плотины, водонефтяного контакта, контура профиля крыла самолета и т. д.) находится по заданным характеристикам, либо характеристики рассчитываются при заданной его форме. Первые задачи получили название прямых краевых задач, а вторые — обратных [1]. В частности, эти задачи возникают в разведочной геофизике при поиске нефтяных слоев и при выборе параметров волнового воздействия на месторождения нефти и газа с целью интенсификации добычи. Развитие моделей фильтрации в пористых средах, являющихся определяющими в решении геофизических задач, началось во второй половине XIX столетия. В основу научной разработки большинства вопросов фильтрации был положен закон сопротивления при фильтрации жидкости, установленный экспериментальным путем в 1856 г. французским инженером А. Дарси. Закон выражает пропорциональность скорости фильтрации флюида градиенту напора. Коэффициент фильтрации характеризует среду и жидкость одновременно, т. е. зависит от размера частиц, их формы и шероховатости, пористости среды, ее проницаемости, вязкости жидкости. Первые теоретические исследования фильтрации, основанные на этом законе, были начаты Ж. Дюпюи и продолжены Ф. Форхгеймером. Первые двухскоростные математические модели для описания распространения сейсмических волн в насыщенных жидкостью пористых средах были разработаны в работах Я. И. Френкеля, М. Био [2, 3]. Неизотермическая модель фильтрации в предположении аддитивности энтропии компонент пористой среды была получена методом законов сохранения в работе П. Робертса, Д. Лопе [4]. Континуальная теория фильтрации, не ограниченная предположением такого рода, была построена в работах В. Н. Доровского [5, 6] также в рамках

• © 2013 Имомназаров Х. Х., Имомназаров Ш. Х., Рахмонов Т. Т., Янгибоев З. Ш.

2.    Постановка задачи

метода законов сохранения. Закон Дарси получается в качестве следствия уравнений упомянутых теорий в одном из предельных случаев.

Последние десятилетия внимание математиков направлено на так называемые некорректные задачи, т. е. задачи, у которых решение может не существовать или быть неединственным, неустойчивым. К числу таких задач относятся и многие обратные начально-краевые задачи математической физики. Ряд математических постановок обратных задач теории распространения волн для модели упругих сред впервые был рассмотрен А. С. Алексеевым [7, 8]. Обнаружилась их связь с одномерными обратными спектральными задачами, рассмотренными И. М. Гельфандом и Б. М. Левитаном [9], а также М. Г. Крейном [10, 11]. В работе [12] установлена связь метода Баранова — Кюнетца с дискретным аналогом метода Гельфанда — Левитана. При этом условия разрешимости уравнений Гельфанда — Левитана фактически приводили к возможности коррекции неточно заданных сейсмограмм. Достаточно полную библиографию по теории обратных задач для уравнений гиперболического типа можно найти в [13–23].

В данной работе, используя идеи работы [23], строятся регуляризирующие алгоритмы для динамических обратных задач для одномерного уравнения SH волн в насыщенных жидкостью пористых средах, в которых происходит потеря энергии при межкомпонентном трении.

Пусть полупространство z >  0 заполнено неоднородной пористой средой. Уравнения распространения сейсмических SH волн с учетом поглощения энергии, обусловленной коэффициентом межкомпонентного трения b(z), имеют вид [24, 25]

Ps(z)utt = (^(z)Uz )z - Pl (z)b(z)(ut — Vt),(1)

Pl(z)vtt = Pl(z)b(z)(ut - Vt).(2)

Здесь u и v — компоненты векторов скоростей смещений частиц упругого пористого тела и жидкости с парциальными плотностями p _s (z) и p i (z) соответственно. Предположим, что пористая среда покоится при t <  0:

u|t=0 = Ut |t=0 = 0,(3)

v|t=0 = vt |t=o = 0.(4)

Пусть на границе z = 0 приложена сила:

^Uz |z=o = 5(t)(5)

Здесь 6(t) — функция Дирака.

Требуется по информации (5) и по заданным один раз непрерывно дифференцируемым положительным функциям p _s (z), ^(z), непрерывным положительным функциям P l (z), b(z) определить дважды непрерывно дифференцируемые функции u(t,z) , v(t,z) из (1)–(4). Такую задачу будем называть прямой динамической задачей для уравнений SH волн в пористой среде.

В приложениях наибольший интерес представляют задачи об определении переменных коэффициентов дифференциального уравнения. Это связано с тем, что дифференциальные уравнения, как правило, описывают физические процессы, а коэффициенты уравнения связаны с физическими характеристиками среды, в которой протекают эти процессы. Так как непосредственно эти коэффициенты измерить невозможно, то задача об определении свойств вещества является, по существу, обратной.

Используя методику предложенную в [23] для обратной задачи теории упругости, построим регуляризирующий алгоритм следующих обратных задач:

Задача 1. Требуется по информации u|z=0 = ф(t)                                              (*)

восстановить ^(z) из (1)-(5) (при этом считаются известными остальные функции р s (z), P l (z), b(z) = x(z)P l (z))-

Задача 2. Требуется по информации ( * ) восстановить р s (z) из (1)-(5) (при этом считаются известными остальные функции x(z), P l (z), ^(z))-

Задача 3. Требуется по информации ( * ) восстановить x(z) из (1)—(5) (при этом считаются известными остальные функции p s (z), p i (z), ^(z))-

Задача 4. Требуется по информации ( * ) восстановить р i (z) из (1)-(5) (при этом считаются известными остальные функции p s (z), ^(z), x(z))-

3.    Сведение к канонической форме

Введем вместо z координату x:

z

Z dξ x = / ct (0 , где ct(z) = ^jP'S^) есть скорость распространения поперечных сейсмических волн в пористой среде.

После перехода к координате x скорость распространения сейсмических волн в пористой среде становится равной единице. Так как д 1 д

∂z   ct ∂x , то уравнения (1), (2) имеют канонический вид

U tt    U xx = (ln ст) U x    b(x)        (ut   v t ), P s (x)	x > 0,	(6)
v t = b(x)(U - v), x > 0,		(7)
u | t =0 = u t | t =0 = 0,		(8)
v | t =0 = 0,		(9)
I _ ^(t) u x | x= 0 = ст(0)'		(10)

В формуле (6) ст(х) = ^^(x)ps(x ) — акустическая жесткость, ст > 0. Далее предположим, что выполнены

0 < P0s 6 Ps(x) 6 P00s < го, 0 < P0l 6 Pl(x) 6 Pool < ro, 0 < b0 6 b(x) 6 b00 < ro, где p0s, P0l, b0, P00s, P00l, b00 — заданные постоянные.

Теперь обратная задача 1 переформулируется следующим образом: пусть на отрезке [0, T] задана функция u|x=0 = Ф(t), t G [0,T],                                     (12)

и требуется определить ст(x), x G [0, T/2]. Обозначим через A оператор решения прямой задачи, ф = A ln ст, ст G C 1 [0,T/2], и обозначим через Ф образ пространства C 1 [0, T/2] при отображении A.

Следуя работам [7, 8, 21-23], можно показать, что Ф — множество в C ¹ [0, T], определенное равенством

Ф = |ф g C 1[0,T] : ф(0) < 0, kψk2L2 (0,T)

+

T/ 2 T/ 2 ZZ

ф ( | t — s | )^(t)^(s) dtds >  0, V ф G L 2 (0,T ) 0 ,

- T/ 2 - T/ 2

причем оператор A является гомеоморфизмом C 1 [0,T] на Ф.

4.    Регуляризирующий алгоритм

Пусть вместо функции ф = A ln ст известно ее приближенное значение ф G C 1 [0, T], кФ — фк 6 5. Если ф G Ф, то в силу непрерывности A ^-1 на Ф в качестве приближенного значения ст можно взять СТ = exp[A ^-1 ф]. Будем предполагать, что ф G C 1 [0, T], ф(0) < 0, но, вообще говоря, не принадлежит множеству Ф. Естественный метод нахождения приближения в этом случае состоит в построении отображения R : Ф ^ C 1 [0, T/2], Ф = {ф G C 1 [0, T] : ф(0) < 0 } , аппроксимирующего обратный оператор A ^-1 на Ф и определенного на всем множестве Ф [7, 8, 21-23].

Как показано в [21, 22], исходная обратная задача сводится к нелинейному уравнению типа Вольтерра. В данной работе, следуя [23], предлагается регуляризирующий алгоритм, сохраняющий его «вольтерровость».

Прежде всего покажем, что оператор A действует из C 1 [0, T/2] в C 1 [0, T], причем (A ln ст)(0) = — 1/ст(0) < 0. Пусть ст G C 1 [0, T/2]. Будем искать решение задачи (6)-(10) в классе кусочно-гладких функций вида

u(x, t) = 9(t — x)u д (x, t),

v(x, t) = 9(t — x)v д (x, t).

Здесь 9(t) — функция Хевисайда, и д , v д — сужения u, v на замкнутую область 4 = { (x, t) : 0 6 x 6 t } , u д ,v д G C 1 ( 4 ).

Тогда из (6)-(10) вытекает, что при любом T >  0 сужения u, v на треугольник 4 (T) = { (x, t) : 0 6 x 6 t 6 T — x } , которые будем обозначать снова через u, v , должны удовлетворять соотношениям

Lu ≡ u tt

-

u xx = (In ст) u _x

— b(x) ^{P l}   (u _t — v t ),   0 < x < t < T — x,

P s ^(x)

v t = b(x)(u — v),  0 < x < t < T — x,

U x | x =0 = 0, 0 6 t 6 T,

u(x, x)

Pa(Q)a(x)

-

b ( y ) Pl ( y ) 2 ps ( y )

dy

Q 6 x 6 T/2,

v | t =0 = Q, Q 6 X 6 T/2.

Нетрудно видеть, что задача (13)–(17) эквивалентна уравнениям

u(x, t) = Ш

t + X

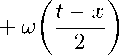
^(Q)

-

-

x

2/(ln a) 0 (0 di J' U(i,Z ) dZ

(t+x)/2                t+x—§                   (t—x)/2

+ | j  (ln a) 0 (0 di  J'  U(i,Z ) dZ + | j  (ln a) 0 (£) di j  U(i,Z ) dZ

0                      §                          0

x

+ 1 / b® Pf,

² J      P s ⁽ⁱ⁾

t+x—§                    z di j (w(€,Z) - b(i)j t—x+§                   0

e ^{b (} § ^{)( z s )} u(i,s) ds) dZ

(t+x)/2                t+x-§                     z di [ (w(i,C) - b(i)

- ¹ f b(^) P=1

² J         P s ⁽ⁱ⁾

■ u(_{,^s)

(t-x)/2               t-x-§                     z di j (w«,<) - b(i)

-1 / *0^

² J ^p s ⁽ⁱ⁾

/^{e— b (} § ^{)( z — s ) u(i}’^{s) ds})^dZ’

t

b®)!®^ ^u<^x,^s) 0

-------------- — Rx b(y)Pl(y) dy где U = ux, W = ut, w(x) = -1/y/a(Q)a(x) e Jo 2ps(y) y. Дифференцируя (18) по x и t, получаем интегральные уравнения на функции U(x,t), W(x,t), u(x,t), решение которых существует и единственно в C(4(T)). Подставляя U(x, t), W(x, t) в (18), найдем решение u(x,t) (из класса C 1) задачи (13), (15), (16). Подставляя u(x,t) в (19), найдем решение v(x,t) задачи Коши (14), (17). Отсюда в частности вытекает, что функция ф(t) = u|x=0 будет из C 1[Q,T] и ф(Q) = -1/a(Q) < Q, т. е. ф G Ф.

Покажем теперь, что уравнение A ln a = ф, ф G Ф, эквивалентно уравнению Вольтер-ра. Для этого введем в рассмотрение банахово пространство Z вектор-функций

z(x,t) = (zi (x,t),Z2 (x,t),Z3 (x),Z4 (x)) , непрерывных на 4(T), с естественно определенной операцией умножения на скалярные функции из C (4(T)) и нормой kzk = max {kzi||, ||z21|, ||z31|, ||z41|}.

В Z выделим подмножество Z 0 , состоящее из вектор-функций вида

Z 0 (x,t) = (Pф)(x,t)

= 1 2 ^{ф (}t^{+ x) -} 2 ^{ф (}t^{- x)}, 2 ^{ф (}t^{+ x) +} 2 ^{ф (}t - ^x), ^{ф (2x)}, ¹M^Q)!,  ^ф е ф . ⁽²⁰⁾

Очевидно, между Z q и Ф имеется взаимно однозначное соответствие. Если в (20) ф Е Ф, то будем писать z q Е Z q . Определим оператор M : Z х R ₊ ^ Z , R ₊ = { t : t >  0 } , формулами:

x

(M (z,a)) i (x, t)

j f ⁽z, ^{a)(e) [}z i ^(e, t + x - ^{e) +} z i ^(e, t - x ^{+ e)]} d^e q

+ 2

x b«' Pl^

J      P s ^(e)

Q

n z i^ t⁺ x - ^{e) +} z i ^(e, t - x ^{+ e) +} z 2 ^(e, t⁺ x - ^e)

t+x - ^

+ Z 2 (e,t - x + <) — b(£) j e ^{- b}® ^{( t + x - 5 - s )} Z 2 (e,s) ds

Q t-x+£

- b (0 j e -^- x+t - s^e^ dsO de, Q

x

(M(z,a)) 2 (x,t) = j f (z,a)(e) [z i (e,t + x - e) - z i (^,t - x + e)] de Q

x

. Z b<« ^

2 J     Ps«)

Q

n z i ⁽€, t⁺ x ^{- e) -} z i ^(e, t^- x ^{+ e) +} z 2 (£i t⁺ x - ^)

t+x - ^

- Z 2 (^,t - x + <) - b(^) j e - b^^^^t+x-^ - s) Z 2 (e,s) ds

Q t-x+^

+ b(O J e

Q

x

-

b ⁽ S ^)(t-x+ S ^-s) Z 2 (^,s) d^d^,

x

⁽M ⁽z,^a)) 3 ^(x)=² f f^(z,a)(^^)z i ⁽^, ^{2x -} ^) de ⁺ f ^b(£)-^Pl(|⁾ n z i ⁽^,^{2x -} ^) P s (^)

Q

Q

2 x - ^

+z 2 (e, 2x - e) - ь(^) у e-b^-^s Z 2 (^,s) dsO de, Q

x

(m (z,a))4 (x) = - j f (z,a)(e)z4 (e) de, Q где f (z, a) = Z3Z4/(1 + az3)(1 + az4).

Лемма 1. Уравнение z = z q + M (z, 0) , z q Е Z q , разрешимо в Z тогда и только тогда, когда z q Е Z q .

• <1 Пусть z q Е Z q . По определению множеств Z q и Ф это означает, что существует функция

ст Е Ci[0,T/2], a> 0, такая, что A ln ст = ф, где ф однозначно определяется функцией zq согласно (20). Далее, по определению ф(t) = u|x=Q, t Е [0,T], где u(x,t) — решение задачи (13), (15), (16)

с функцией ст = exp[A ^-i ф]. Покажем, что тогда вектор-функция

z(x,t) = ( u x (x,t),u t (x,t), [u(x,x)] , 1/u(x,x) )

удовлетворяет уравнению z = zo + M(z, 0). Действительно, обращая волновой оператор d2/dx2 — d2/dt2 по формуле Даламбера с учетом данных Коши u|x=g = ф(t), ux|x=o = 0 и вытекающего из (16) соотношения bρl

f^(z, ^{0) +} TT" 2ps

u' + bp i u 2p s

— ct)'

находим

x

t + x —

u(x,t) = 2ф(t + x) + |ф(t — x) + jf (z, 0)(^) de j zi (£,<) dz 0

x               t+x-^Z

+ 1 [b)P e d^ [ { z i (e,z)+ z 2 (^,z) — b(£)   e-< ^)(Z-s) z 2 (^,s) ds } dz.

• 2 J       Ps(^)      J                                      J>

0               t-x+^0

Отсюда дифференцирование по x приводит к равенству zi(x,t) = zoi(x,t) + (M(z, 0))i(x,t).

Дифференцируя обе части равенства (22) по времени, получим z2(x,t) = zo2(x,t) + (M(z, 0))2(x,t).

Затем, полагая в (22) t = x, дифференцированием получим za (x) = zga(x) + (M (z, 0))a (x).

Наконец, по определению z4(x) = —za(x)z4 (x), откуда вытекает, что z4(x) = zo4 + (M(z, 0))4(x).

Обратно, пусть z ∈ Z — решение уравнения z = zo + M(z, 0), zo G Zg-

Тогда функция z 4 (x) G C ¹ [0, T/2] удовлетворяет соотношению z 4 + f (z, 0)z 4 = 0, условию z 4 (0) = 1/ф(0) < 0 и, следовательно, везде отрицательна. Положим

x

u(x, t) = ф(t) + [ zi(^, t) de, (x, t) G 4(T), o                                                       (23)

-X b(y) etil dy ct(x) = — z4(x) e 0 Ps y , x G [0, T/2], где ф — функция из Ф, соответствующая zo. Покажем, что пара (u, ст) удовлетворяет равенствам (13), (15), (16). Действительно, по определению ux = zi, ст /ст = 2z4/z4 =

—2f (z, 0) и, следовательно,

u(x,t) = ф(t) + 2

ξ

x

∂∂ξ t+S-n

ф(t + i) + ф(t - i)

ζ

-

⁺ [ ^b(n) ^M dn [ {u z ⁽n^,z) ^{- b(}n) / ^e J      Ps(n)      J                      J

t - S+n

= ^ ^{ф(t + x) +} ^ ^{ф(ф — x) —}

xt

• +    ¹ / b(i) ^ di /

• 2    J      Ps(i)J

x

• 1    [ о (0

• 2    J <)

ζ

^s 0          ^t+S- n

- [ °т^П2 dn [ U n (n,Z ) dZ

J o(n) J

0           t - S+n

^{b(n)(z - s )} u _s (n, s) ds^ dZ^ di

t+x-S di J us(i,Z) dZ t-x+S

u z «,Z ) — b«) J e - b^ - s

u _s (i, s) ds^ dZ.

Отсюда видно, что u E C 1 (4(T )) и выполняются равенства (13), (15).

Проверим выполнение (16). Полагая в (23) t = x и дифференцируя, находим d ,     , z , d 1 X

—u(x, x) = z ₃ (x) = — —— . dx                  dx \Z 4 (x) /

В силу того, что z ₄ < 0, из (23) вытекает равенство

,____________ xb      ' dy z4(x) = — pa(0)a(x) e0  Ps v

.

Тогда

__________ - X b k v l PlM _dy                i                 i u(x, x) + 1/ P a(0)a(x) e ^{0 2ps(v)}    = u(0, 0) + ^(0) = Ф(0) - z^-^ = 0.

Итак, пара (u, о), u E C 1 ( A (T)), о E C 1 [0, T/2], о > 0, удовлетворяет равенствам (13)(17). По определению множества Ф отсюда вытекает, что функция ф(t) = u | _x =o принадлежит Ф, а следовательно, z o E Z o . B

Таким образом, установлено, что решения уравнений A ln о = ф, ф E Ф, и z = z o + M (z, 0), z o E Z o , равносильны. Пусть теперь вместо функции ф E Ф задано ее приближенное значение ф E Ф, кф — ф к 6 5, причем для простоты будем считать, что ф(0) = ф(0) (неравенство ф(0) = ф(0) не вносит принципиальных изменений). В терминах функций z o = Рф и z o = Рф это означает, что z o E Z o , z o E Z o и ||z o — z o k 6 5. Если z o не принадлежит Z o , то по лемме 1 уравнение z = z o + M (z, 0) не имеет решений.

Перейдем к исследованию регуляризованного уравнения z = z o + M(z,a) , a > 0. Пусть B _r — шар в Z радиуса r ,

B r = {z E Z : | z | 6 r } ,

| z | (x)=max< sup | z ₄ (x,t) | , | z 2 (x,t) | , | z a (x) | , | z 4 (x) | >, z E Z. x 6 t 6 T - x

Лемма 2. (1) M E C 1(Z x R+; Z), т. е. оператор M непрерывен из Z х R+ в Z и имеет непрерывные частные производные Mz(z, a), Ma(z, a).

• (2)    Для любых z G Z , a >  0 ,

x

H M(z,a) H (x) 6 2a / H z H (i) di,

X G [0,T/2],

где c i (a,T ) = (1 + 2b oo p^l)(1 + 2Tb oo ) .

1 0 Is

• (3)    Для любых r >  0 , a > 0 , z G B r , y G B r ,

x

HM (z,a) - M (y,a) H (x) 6 C 2

( r, a, T )

Hz — уН(1) di, x G [0,T/2],

где C 2 (r,a,T ) = ( 1 + 4r V « + b oo " O'/ ' a)(1 + 2Tb oo )/(2a) .

^p 0 ,s

C Первое утверждение очевидно и проверяется непосредственными вычислениями. Заметим, что оператор M _z : Z x R + ^ L(Z; Z ) при любых фиксированных z, a является линейным непрерывным оператором Вольтерра. Докажем неравенство (25). Из определения оператора M вытекает, что для любого a >  0

x

H M(z,a) H (x) 6 2 / f|f(z,a) | + 1 b(i)Pl^) H z ^ Ci)di J \              ^{2      p} s ^{(| )}/

0 x

+ 1 [ ⁶di.

2          P s ( i )

Отсюда с учетом (11) и неравенства | f(z,a) | 6 1/(4a) [23] получим неравенство (25). Неравенство (26) доказывается аналогично, если учесть, что функция f (z, a) удовлетворяет неравенству [23]

^{|f(z,a) - f(}y^,a)| 6      max {| z i — У 1 1 , | z 2 — У 2|} • ▻

α

Рассмотрим теперь регуляризованное уравнение z = zo + M(z, a).

Теорема 1. Пусть z o G Z . Тогда для любого a >  0 в Z существует единственное решение z(a) уравнения (27) , более того, как функция параметра a оно непрерывно дифференцируемо в R + и

H z(a) H 6 H z o II exp(c i T/4a). (28)

C Установим сначала априорную оценку (28). Пусть z(a) G Z — решение, отвечающее значению a > 0. Из неравенства (25) следует, что x

H z(a) H (x) 6 H z o H + 2a / H z(a) H (i)di, x G [0,T/2],                 (29)

и оценка (28) получается применением неравенства Гронуолла к (29).

Покажем единственность решения. Пусть z(a), y (a) G Z — два решение уравнения (27). Поскольку оба решения лежат в шаре B r( _a ) , r(a) = ||z 0 || exp(c i T/4a), то на основании леммы 2 их разность w(a) = z(a) — y(a) удовлетворяет неравенству

x

^|w(a)k(x) 6 ^с2^{(г(а),а,т} ) j ||z ^— y^) <, x ^E [^T/²]

которое для любых a >  0 имеет единственное решение w(a) = 0, т. е. z(a) = y(a) .

Докажем существование решения методом последовательных приближений.

z ^{( n +1)} (a) = z ₀ + M(z ⁽ⁿ⁾ (a), a'), n >  0, z ⁽⁰⁾ = z ₀ .

Используя неравенство (25) и принцип индукции, нетрудно показать, что для n >  0

Имеем

(30) любого

n

"'(a) H (x) 6 k zJ fl X 1(yx) 6 k z) fl exp(c i T/4a), —* k! \ 2a /

k =0

т. е. все приближения лежат в шаре B r ( _a ) .

Рассмотрим последовательность w ^{( n )} (a) = z ^{( n +1)} (a) —

k w ⁽⁰⁾ (a) | = | M(Z 0 ,a) | 6 C 3 « z (0) k ,

- z ^{( n )} (a). Имеем

_ ciT c3    4a ,

x

| w ^{( n )} (a) | = \\ M(z n (a),a ) — M ( z ^{n -1} (a),a )| 6 c ₂ (r(a),a,T ) j | w ^{( n -1)} (a^W, 0

n >  1,

и следовательно, для любого n >  0

| w ^{( n )} ( a ) | 6 C 3 |Ы|¹ ( c 2 TY'. n! \ 2 ;

Отсюда вытекает, что ряд Z 0 + Р П =0 w ⁽ n ) (a) мажорируется сходящимся числовым рядом

1 CeTT\ kz0k + c3kz(0)k 52 n ( у ) = kz0 11(1 + c3e 2T/^

n =0

и, следовательно, последовательность

n

z ^{( n +1)} (a) = z ₀ + M ⁽z ^{( n )} (a),a ) = z ₀ + X w ^{( m )} (a)

m =0

сходится в Z . Поскольку все z ^{( n )} (a) E B r ( _a ) , то

z(a) = lim z ^{( n )} (a) E B _r ( _a ) .

n →∞

Переходя в (30) к пределу, в силу непрерывности оператора M получаем, что z — решение уравнения (27).

Непрерывная дифференцируемость решения z(a) вытекает из теоремы о неявной функции [26]. Действительно, согласно лемме 2 оператор G : Z х R ₊ ^ Z , G(z, a) = z — Z 0 — M (z, a), имеет непрерывные производные G _a = — M _a , G _z = I — M _z . При этом для любых (z, a) E Z х R ₊ , G z (z, a) : Z ^ Z имеет ограниченный обратный оператор (в силу того, что M z (z, a) — линейный непрерывный оператор Вольтерра). Следовательно, по теореме о неявной функции z(a) E C ¹ ( R + , Z ). B

Рассмотрим случай z o G Z o . Тогда согласно лемме 1 в Z существует единственное решение z(0) уравнения z = z o + M (z, 0) (единственность решения следует из единственности исходной обратной задачи [21, 22]). Следовательно, если z o G Z o , то уравнение (27) разрешимо в Z единственным образом для любых а >  0. Нетрудно видеть, что в этом случае решение z(а) будет непрерывно дифференцируемым на замкнутой полуоси R ₊ . Действительно, по теореме 1 достаточно доказать гладкость z(a ² ) в окрестности точки а = 0. Последнее вытекает опять из теоремы о неявной функции, поскольку существует решение уравнения G(z, 0) = 0, G G C ⁺ (Z х R , Z), где G(z, а) = G(z, а ² ), и оператор G _z (z(0), 0) имеет ограниченный обратный. Сформулируем этот результат как следствие из теоремы 1.

Следствие. Если z o G Z o , то решение уравнения (27) существует и единственно в Z для всех а >  0 и принадлежит классу в C ¹ ( R + , Z ) .

Вернемся теперь к исходной задаче. Итак, нам известна функция ф G Ф такая, что ф(0) = ф(0), кф — фк 6 5 , ф G Ф. Следовательно, z o = Рф G Z o и z o = Рф G Z o , k z o — z o k 6 5.

Рассмотрим уравнение z = z o + M (z, а). По теореме 1 при а > 0 оно имеет единственное решение в Z . Обозначим его через 5(а). Решение уравнения z = z o + M(z, а), а > 0, обозначим через z(а). Напомним, что z(0) соответствует точному решению обратной задачи. Функция Z(a) порождает оператор R : Z o х R + ^ Z , R(z o , а) = 5(а). Следующая теорема по сути утверждает, что этот оператор является регуляризирующим для уравнения z = z o + M(z, 0).

Теорема 2. Пусть 5 6 5 o . Тогда существует функция а(5) G C(0,5 o ] , а > 0 , lim^ o а(5) = 0, такая, что lim^ o Р( а(5)) — z(0) | = 0.

C В силу неравенства треугольника ^ г(а) — z(0) | 6 ^ г(а) — z(а) k + ||z(а) — z(0) | . Пусть α 6 α 0 , где число α 0 будет указано позже. Согласно следствию из теоремы 1, функция z(а) G C ¹ ( R + ,Z) и, следовательно, существует константа С ₁ такая, что для всех а G [0, a o ] ||z(а) — z(0) | 6 C i а. Оценим разность Z(а) — z(а):

Р(а) — z(а) k (x) 6 ||zq — z o | + ||M(г(а),а)) — M (z(а), а)) | (х).

Как и при доказательстве (26), нетрудно получить неравенство

x j Р(а) — zMIIK)d6

| M(Z(а),а)) — M На),а))||(х) 6 Г + 2^1 2а      а

Заметим, что нормы kz(а)k равномерно ограничены на R+ некоторой константой 1, зависящей от zo. Это следует из непрерывности функции z(a) на R+ и оценки (28). Таким образом,

x

||Z(a) — z(а)k(x) 6 5 + — / ||Z(а) — z^)^) d£, α x G [0,T/2],

где C ₂ = (c i + 41^q q )/2, откуда в силу неравенства Гронуолла получим оценку

р(а) — z(^) | (x) 6 5e ^C 2 ^{T/ 2 a} .

В результате приходим к неравенству

||Z(а) — z(0) | 6 C ₁ а + 5e ^C 2 ^{T/ 2 a} .

Теперь достаточно взять

_ Ci + 4ivao t = 1 + ln(5o/5) 2 , где ao = (tI + pT212 + C1 T/2)  = a(5o). Тогда kz(a(5)) — z(0)k 6 C1 a(5) + Ve5o5 ^ 0,

• 5 ^ 0. B

Из доказательства теоремы видно, что оператор R будет равномерно регуляризирую-щим оператором на любом подмножестве Z oi множества Z o вида Z oi = {z o ^ Z o ^: 1(z o ) <1} .

Множество Z _{0 l} принято называть множеством корректности рассматриваемой обратной задачи [27].

Замечание. Соответствующие леммы и теоремы имеют место для обратных задач 2, 3 и 4. Для исследования обратных задач 3 и 4 надо взять вектор-функцию z(x, t) в виде

z(x,t) = [u _x (x,t),u t (x,t), [ u(x, x) p a(0)a(x) ]

___________1___________

u(x, x) pa(0)a(x)

В заключение авторы выражают благодарность Перепечко Ю. В. за обсуждение проблемы и за ряд ценных замечаний, которые были учтены при подготовке статьи.