Rehabilitation of Rutherford's Atom Model

Rehabilitation of Rutherford's Atom Model

Annotation

It is shown that in the planetary model of the Rutherford atom there are stable in height - stationary orbits of the electron, the reason for the stability and discreteness of stationary orbits is substantiated.

They write [1] that “Rutherford's planetary model of the atom corresponds to modern concepts of the structure of the atom with refinements ... The disadvantage of the planetary model was the impossibility of explaining the stability of atoms by it. Since electrons move ..., then, according to the laws of classical electrodynamics, they must emit electromagnetic waves, losing the kinetic energy of orbital motion to radiation and as a result "fall" onto the nucleus. Calculations performed using the methods of classical electrodynamics show that electrons should “fall” onto the nucleus in a time of about 10-11 s.”

These refinements are known to have led to the creation of quantum mechanics. These refinements are known to have led to the creation of quantum mechanics. Let us consider in more detail the interaction of an electron and a nucleus using the methods of classical electrodynamics.

As you know, a uniformly moving charge does not radiate in a vacuum. However, even a uniformly moving electron constantly remagnetizes the atomic nucleus, i.e. it transfers its energy to it and thus, naturally, loses its kinetic energy [4]. In addition, the charge creates a flow of energy moving with the charge in a limited vicinity of the charge [3].

Indeed, only a moving charge emits, which follows from the Larmor formula [2]. It will be shown below that the Larmor radiation of an electron interacts only with the atomic nucleus.

Thus, the electron transfers its kinetic energy to the nucleus in two ways. However, let us consider how destructive the radiation processes are for the conservation of the kinetic energy of an electron.

Omega

F4

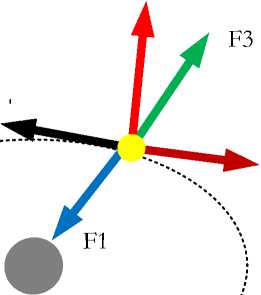
F2

Fig. 1.

Consider an electron with mass m, which rotates around its own axis with an angular speed < 1 and moves along a certain trajectory around the nucleus with a linear speed V - see Fig. 1. The acts on the electron force of gravity

F = mg , (1) where g is the acceleration of free fall of an electron onto a nucleus; Coriolis force

F 2 = — 2mto 1 x v (2) and centrifugal force

F 3 = mo 2 R, (3) where R, < 2 are instantaneous radius and angular speed of rotation at a given point of the specified trajectory.

An electron loses its kinetic energy due to radiation. Lost electron power P ₄ expended by the electron can be defined as the power of some force F₄ of resistance to the movement of the electron, i.e.

P 4 = F 4 V. (4)

Let the vector О 1 have three projections - the projection <0 1^ onto the radius, the projection О^ onto the tangent to the circle, and the projection <017 onto the vertical. Let us also consider the projection of

^IRO onto the plane of the circle, the projection of “izo onto the vertical plane tangent to the circle, and the projection of “izr onto the vertical plane passing through the radius.

Body movement will be stable under three conditions:

Fi = -2m“ iroV (5) F3 = -2m“ izoV (6) F4 = -2m“ izoV, (7) where the projections of the Coriolis force are indicated on the right.

From (4), taking into account (7), we find:

P4 = -2m“izoV2.

Formulas (1, 5) can be combined. Then we get:

9 = -2“iRoV

Formulas (3, 6) can be combined. Then we get:

“2R = —2oizoV(10)

From (8, 9, 10) we find:

“izo = -2^^,

(iro = -2^ -

“izo = -y.

In these formulas, formula (7) is not obvious. It indicates the force of resistance to the motion of an electron, acting along the speed V , and the projection of the Coriolis force on the same speed. Such a projection is equal to zero by definition (2). The explanation is given in the appendix and is based on the fact that the real trajectory of an electron is a spiral line. It was shown there that at a certain "height" above the nucleus an electron orbit can exist that retains its height, the stability and discreteness of such stationary orbits is substantiated

Thus, if m, g, “2,R are known for an electron, then projections and the speed vector “1 can be found from (11, 12, 13). And vice versa, if the vector “1 is known, then the speed “2, the radius of the orbit R and the acceleration g can be found from (11, 12, 13). The latter value for a particular nucleus determines the "height" of the orbit. Hence, электрон с определенной скоростью (У^ имеет однозначно определенную орбиту.

The energy of rotation of an electron around its own axis with a speed ( 1 and its angular momentum does not change. The energy of rotation of an electron around a circle

W = 0.5mv² = 0.5mo) 2 R² (14) does not change, since the speed (₂ and the radius R of the orbit do not change. The conservation of these values occurs despite the fact that the electron is constantly losing its own energy, because the energy of the electron is constantly restored by the Coriolis force.

Such an action of the Coriolis force is possible only if it can do work, i.e. this power is real force. A mathematical proof of the reality of this force is given in [2, Section 3]. There it is shown that the Coriolis force can be justified as a consequence of Maxwell's equations, and the source of energy for this force is the electric core.

The opponent can say that the energy of the nucleus is not infinite and, in the end, it will be wasted on generating Coriolis forces for all electrons. I agree with him - I agree that this waste is contributing to nuclear decay. But this is not a reason to abandon the planetary model.

Rutherford's model of the atom must be returned to physics.

Application

It was shown in [3] that an electron in a vacuum moves along a spiral trajectory, which is a solution to the Maxwell system of equations [2]. In cylindrical coordinates r, p, z stream functions have the form:

Jr = qvT cos(ap + /z), (1)

Jp = qVp sin( ap + /z), (2)

J z = qv _z sin( ap + /z), (3) where q is the electron charge, a, / are some constants, V _T , V p , V _z are constants - the speeds of the electron along the coordinates. In this case, r = const . In fig. 2 shows three helical lines described by the functions (10, 11) of the projections J _p and J_z of the current. In fig. 1 shows for example: a thick line at a = 2, / = 0.8 , a middle line at a = 0.5, / = 2 , and a thin line at a = 2, / = 1.6 .

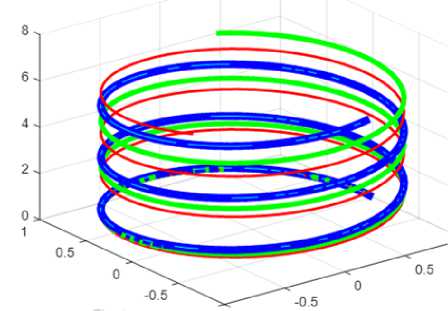
Fig. 2

In what follows, we will consider functions of coordinate-wise speeds

VT = ^ = W cos(p),(4)

in parametric form with the parameter p = ap + xz.(5)

Thus, the electron moves at a speed

V = [V, V, Vz],(6)

where

V = vr cos( p),(7)

V = v

V = vz sin( p).(9)

Let us pass to Cartesian coordinates and further consider the vector

V = [V, Vy, Vz],(10)

where

V = V cos( p) -Уф sin( p),(11)

V = V sin(p) + V cos( p).(12)

or, taking into account (8, 9),

V = vr cos(p) cos( p) — гф sin(p) sin( p),(13)

V = vT cos(p)sin(p) + vv sin(p) cos(p).(14)

It is important to note further that functions (13, 14) are periodic functions of the z coordinate , which follows from (5).

If an electron rotates around its own axis with an angular speed O), then the Coriolis force acts on it

F _c = —2m6) x V,                          (15)

where m is the electron mass. Wherein

F =	"Fx , F y , F z ] ,                                  (16)
to =	tox , to y , to z ] ■                                     (17)
From (10-12) we find:
	Fx   toyVz tozVy 1
F =	F y = to z V x -to x V z .                 (18)
	F z = to x V y - to y Vx\

It can be seen that the Coriolis force has a projection F _z on the z axis, i.e. on the trajectory of the electron. The force F _z is determined through functions (13, 14) and therefore is periodic.

Suppose that the electron revolves around the nucleus and denote the length of the electron trajectory in one closed loop as L . Consider the average value of the force F _z over the length L . and denote it as F _zmtd . Due to the periodicity of the force F _z , the value F_zm t^ can take on values different in sign.

Together with this force, on the electron acts the force F₄ of resistance to the motion of the electron, which is proportional to the length L . Consider the total force acting on the electron along the trajectory:

F trek = F zmta - FL                      (19)

Wherein

• 1.    if F t_rek = 0 , then the trajectory length does not change.

• 2.    if F trek >0 ,then the electron is accelerated, gradually removed and its trajectory is lengthened,

• 3.    if F t_rek < 0 , then the electron slows down, gradually falls on the nucleus, and its trajectory is shortened.

You can also consider the derivative """^~ at a point with such a value of L, where F t_rek = 0 . For """~~ < 0 , the trajectory is stable. Indeed, with decreasing altitude, the length L decreases, but at the same time F t_rek increases, the electron is accelerated, and while at the same time it rises.

Thus, there are trajectories that are stable in height — stationary orbits. These orbits are discretely located in height. The stability of the stationary orbits is provided by the Coriolis force acting on the emitting electron.