Реконструкция 3D-сцен по разноракурсным изображениям при неизвестных внешних параметрах съёмки

Задача восстановления трёхмерных моделей сцен по разноракурсным изображениям является одной из наиболее востребованных в системах компьютерного зрения. При этом типичной является ситуация, когда внешние параметры камер в глобальной системе координат (сдвиг и поворот) не известны [1]. Известно, что эти параметры связаны с параметрами фундаментальной матрицы, которая может быть оценена по набору (не менее семи) соответствующих точек на видах сцены.

Такой путь решения задачи был предложен в работе [2]. Однако вследствие того, что процедуры восстановления трёхмерных моделей крайне чувствительны к неизбежным погрешностям определения параметров фундаментальной матрицы, технология в целом часто оказывается неработоспособной. В работах [3, 4] решается задача определения внешних параметров камер с использованием уравнений Круппа. Наибольшее число известных работ, посвящённых этой проблеме, направлено на исследование различных способов калибровки. Наиболее известные в области калибровки работы [5, 6] решают задачу определения как внешних, так и внутренних параметров камеры, в том числе параметры дисторсии. Однако калибровка камеры проводится с использованием плоского шаблона (например, шахматной доски), что, как правило, неосуществимо в реальных условиях съёмки.

Указанные выше попытки определить матрицу проективного преобразования при отсутствии информации о параметрах сдвига и поворота свидетельствуют об актуальности задачи. Вместе с тем полученные в этом направлении результаты пока достаточно скромны. В частности, используемые технологии и доступные открытые библиотеки пока не позволяют получить достаточно надёжное решение этой задачи для широкого диапазона характеристик разноракурсных изображений.

1. Постановка задачи

Для восстановления 3D-сцены по разноракурсным изображениям будем использовать модель камеры-обскуры [7]. Предполагается, что разноракурсные изображения получены путём перемещения в пространстве одной камеры с известными внутренними параметрами, заданными матрицей:

f 0 u ₀

K =

0 f v ₀ 001

где f – фокусное расстояние камеры, а ( u 0 , v 0 ), – координаты главной точки камеры в системе координат, связанной с камерой.

Пусть M – некоторая точка в глобальной системе координат, которая должна быть восстановлена по паре разноракурсных изображений. Преобразование из глобальной системы координат в однородные координаты изображения имеет вид:

m =

f" 1 v

V 17

~

r11

K ( R I t ) M = K Г 21

V Г 31

r 12

r 22

r 32

r 13

r 23

r 33

t 1

t ²

¹ 3 7

Y

V 1 J

, (2)

где u , v – однородные координаты точек на изображении вида, X , Y , Z – глобальные координаты точки M , а ( R | t ) – объединённая матрица поворота-сдвига, называемая также матрицей внешних параметров .

С учётом связи пиксельных и однородных координат точек:

m ( x , y ) = K 1 m ( u, v )

соотношение (2) можно представить в виде

x

m ⁽ x , y ) = y

V1J

~

f r 1

r ²¹

V ^r 31

r ₁₂

r ₂₂

r ₃₂

, f X 1 ^r 3 t 1 Y r- t 2 Z Г 33 1 3 J ,

V 1 J

Далее под координатами точки m всюду подразумеваются координаты m ( x , y ), удовлетворяющие (4).

С использованием соотношения (4) строится процедура вычисления 3D-координат сцены. В частности, записав с использованием неизвестных множителей g и g' соотношения вида (4) для соответствующих точек m ( x , y ) и m ( x ' ,y ') [8] в виде равенств:

x

y

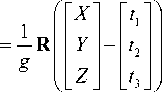
Л г

rx = rl m i = r11 xi + r12 У1 + ri = r2 m i = r21 xi + r22 yt + ri = r3 mi = r31 xi + r32 У1 + r1 =[r11, r12, r13]

а r 2 = [ / 2, . ^r 22 , Г 23 ] >  .

r 3 = [ r 31 , r 32 , r 33 ]

x

/ ^y

= Л R '

Y

g

V-

Z

t ²

.¹ 3 j;

Зададим критерий оптимальности проективного преобразования в виде суммы квадратов разностей координат соответствующих точек на изображениях видов. С учётом обозначений (8), (9), (10) этот критерий представляется в виде:

и приравняв фигурирующие в (5), (6) векторы координат [ X , Y , Z ] ^T , получаем:

g R

-1

x

y

g R ‘

y

= c -

t 1 ^— t 1 ' t 2 — 1 2 ' t 3 — 1 3 '

Соотношение (7) представляет собой систему из трёх уравнений относительно двух неизвестных – g и g '. Посредством подстановки найденных из этой системы указанных множителей в соотношение (5) и/или (6) формируется вектор координат трёхмерной точки [ X , Y , Z ] ^T .

Из соотношений (3)–(7) видно, что для реконструкции 3D-сцены необходимо знать параметры матрицы поворота-сдвига ( R | t ). Проблема состоит в том, что часто эти параметры оказываются неизвестными и вначале требуется определить их по заданным на двух видах координатам N пар соответствующих точек m ( x , y ) и m ( x ′, y′ ). Решению этой задачи и посвящена настоящая статья.

Идея работы состоит в том, чтобы определить параметры поворота и сдвига камер в глобальной системе координат непосредственно по заданным соответствующим точкам видов, исключив промежуточный этап оценивания параметров фундаментальной матрицы.

2. Формулировка задачи оптимизации

Задачу определения параметров сдвига и поворота сформулируем как задачу оптимизации параметров проективного преобразования, обеспечивающего близость (в смысле заданного критерия) соответствующих точек на двух видах. Для компактной записи общей оптимизационной задачи введём обозначения:

Q x = zr + t x Qi = zr? + t y Q i = zr + t z

,

где

N _{2 2}

Q(r,t,z) = Z (xQ — Qix) +(yQ—Qi) , (11) i=1 L j где r = [r1, r2, r3]T – 9×1-вектор параметров поворота камеры, составленный из векторов-строк (10) матрицы поворота R, а Z – вектор, компонентами которого являются глобальные координаты Zi, i = 1, N точек сцены. Заметим, что для векторов-строк матрицы поворота r1, r2, r3 должны выполняться требования ортонормальности.

Поскольку глобальные координаты Z i , i = 1, N , также являются неизвестными, в результате решения должны быть оценены N + 12 неизвестных параметров – компонент вектора Y = [ r ^T , t ^T , Z ^T ] ^T , являющегося прямой суммой векторов r , t , Z . С учётом сказанного задача формулируется следующим образом. Найти

Y * : Q ( Y * ) = mn Q ( r,t , ^Z )                  (12)

при условии

IIГ111=1Г211=1 кз1= 1,

(r1, r2 ) = (r1, r3 ) = (r2, r3 ) = 0, r1 X r2 = r3,  r2 x r3 = r1,  r3 X r1 = r2,

где Q - область допустимых значений параметров сдвига, поворота и координат Z i , i = 1, N .

Поставленную задачу можно переформулировать как задачу безусловной оптимизации, если вместо вектора параметров r = [ r ₁, r ₂, r ₃] ^T оценивать вектор параметров, составленный из углов поворота вокруг осей X, Y, Z . При этом выполнение ограничений (5) обеспечивается тем, что матрица R формируется в виде

R = R_yRvR₇ , XYZ

где

R X

' 10    0 '

0 cos ⁽a ) ± sin ⁽a )

_V 0 + sin ( a ) cos ( a ) _;

	г cos ( в )	0	± sin ( в ) '
R Y =	0	1	0
	V + sin ( в )	0	cos ( в ) ,
	^ cos ( y )	±	sin ( y ) 0 )
R z =	+ sin ( y ) V 0	cos (Y )    0 0       1 X

Здесь знак перед синусом указывает направление поворота.

Выполнив в векторе r = [ r 1 , r 2 , r 3 ] ^T замены, соответствующие представлению (14):

r11 = Cos в Cos y, r12 = Cos в Sin y, rB = Sin в, r21 =- Cos a Sin y- Sin a Sin в Cos Y, r22 = Cos a Cos Y— Sin a Sin в Sin Y, r23 = Sin a Cos в, r31 =- Sin a Sin Y— Cos a Sin в Cos Y, r32 =- Sin a Cos Y— Cos a Sin в Sin y, r33 = Cos a Cos в , задачу (12) можно представить в следующем виде. Найти

• Y * : Q ( Y * ) = min Q ( ф,t , Z ) ,                 (15)

• 3.    Построение вычислительной процедуры

'     ' ф,t,ZеЦ где ф = [a, в, Y], а t и Z те же, что и выше. Подчеркнём, что в данном случае отсутствуют ограничения на искомые параметры.

Сформулированная задача является многомерной и в общем случае многоэкстремальной. Несмотря на устранение ограничений и снижение размерности, она остаётся достаточно громоздкой в вычислительном отношении. Поэтому для её решения воспользуемся идеей блочной многошаговой схемы оптимизации [9], [10], [11].

Представим вектор Y в виде

Y = [ ф T ,T T ] T ,                                 (16)

где T = [ t ^T , Z ^T ] ^T – ( N + 3)×1-вектор, являющийся прямой суммой векторов t и Z . Теперь задача определения минимума в правой части (15) может быть представлена в виде [11]:

min Q (ф,Т) = min min Q (ф,Т), ф,Тей^ ™, 1 феЦ Тейт^™, 1

где Ц_ф , Ц _т - подобласти допустимых значений, являющиеся проекциями исходной области Ц на подпространства, соответствующие макропеременным ф , T соответственно.

Применяя к макропеременным ф, T схему многошаговой оптимизации [10], можно записать алгоритм определения значений ф, T, доставляющих минимум критерию (15) на k-м шаге, в виде следующей после- довательности вложенных оптимизационных задач меньшей размерности:

ф : Q (Yk )= min Q (фk, т (фк)), фк еЦф '*

где т (фк): Q(фк, т (фк )) = min Q(фк,т).

На первом шаге вектор ф ₀ должен быть каким-либо образом задан.

Процедура останавливается, если

|| Аф к|| <Еф , ||At к||<е t, ||AZ к|| <Е Z, где

^{А ф} к = ^ф к ^{- ф} к - 1 , ^{A t} к = t к ^- t к - 1 , ^{A Z} к = ^Z к ^{- Z} к - 1

и

IIA Q (Yk )||<е Q,(20)

где

A Q ( Y k ) = Q ( Y k ) - Q ( Y k - 1 ) , а Е ф , E t , E _Z, е q - заданные положительные числа (пороговые значения). Полученное на k -м шаге значение критерия считается оптимальным: