Реконструкция входящего потока вязкой жидкости по измерениям скорости на доступном участке свободной поверхности течения
Бесплатный доступ
Построен метод и разработан алгоритм определения неизвестного распределения скорости втекания вязкой неоднородной несжимаемой жидкости в общий ее поток по дополнительным измерениям скорости течения жидкости на каком-либо доступном наблюдению участке свободной поверхности этого потока. Задача формализуется как обратная граничная задача для модели движения рассматриваемой жидкости. Задача является, вообще говоря, некорректной и решается вариационным методом. Для этого вводится некоторый функционал качества, представляющий собой среднеквадратичную норму разницы (невязки) между наблюдениями скорости на доступной свободной поверхности и виртуальными скоростями, вычисляемыми с помощью специально поставленной вспомогательной задачи граничного управления, которую обычно называют прямой задачей. В нашем случае управлением является скорость жидкости, втекающей в общий поток на недоступном прямому наблюдению участке границы. Искомое решение задачи есть точка минимума этого функционала. Для ее нахождения используется метод градиентного спуска. Этот метод позволяет построить минимизирующие функционал последовательности с помощью предварительно аналитически найденных градиентов функционала. Реализация метода минимизации сводится к последовательному решению соответствующих задач граничного управления. Проведены расчеты модельного примера.
Вязкая жидкость, модель навье-стокса, обратная граничная задача, вариационный метод, численное моделирование
Короткий адрес: https://sciup.org/147232832
IDR: 147232832 | УДК: 517.968+550.311 | DOI: 10.14529/mmph190407
Текст научной статьи Реконструкция входящего потока вязкой жидкости по измерениям скорости на доступном участке свободной поверхности течения
Опишем содержательную сторону задачи. Пусть жидкость втекает в некоторую область Ω через участок Г 2 границы Г = dQ этой области. Наблюдение за движением жидкости на этом участке невозможно. Возможно наблюдение и измерение скорости движения жидкости на участке Г 0 границы Г ( Г 2 пГ 0 = 0 ). На Г 0 движение жидкости считается свободным. Содержательным примером описанной ситуации может служить истечение жидкости через вертикальную щель или канал на горизонтальную поверхность (рис. 1). Задача состоит в том, чтобы по измерениям скорости движения жидкости на доступной наблюдению свободной поверхности определить неизвестное распределение скоростей втекающей жидкости.
Математическая модель движения жидкости в области Ω включает в себя уравнение Навье– Стокса (уравнение Стокса) и уравнение несжимаемости. На границе Γ области Ω задаются подходящие граничные условия для скорости, давления или напряжения. Соответствующую краевую задачу для определения поля скоростей втекающей жидкости и определения поля скоростей движения жидкости во всей области Ω назовем обратной задачей.
Обратные задачи по своей сущности являются некорректными [1–4]. На практике это приводит к тому, что малые ошибки в задании исходных данных и (или) неустранимые погрешности вычислений приводят к неконтролируемым искажениям в определении решения задачи. Обычно это проявляется в неустойчивости решения или нарушении фундаментальных законов физики, которые лежат в основе математического моделирования. Методы и алгоритмы, представленные в работе, позволяют найти адекватное решение поставленной обратной задачи. Вариационный метод регуляризации Тихонова позволяет заменить исходную некорректную задачу задачей оп-
Короткий А.И., Реконструкция входящего потока вязкой жидкости по измерениям Цепелев И.А. скорости на доступном участке свободной поверхности течения тимизации квадратичного целевого функционала [1-5]. Для решения экстремальной задачи выбран метод градиентного спуска, при этом исходная задача сводится к последовательному решению корректно поставленных краевых задач граничного управления. Для тестирования предлагаемого метода проведен вычислительный эксперимент, демонстрирующий работоспособность предложенного метода. Подобные задачи находят многочисленные приложения в теории и практике [1-7]. Работа продолжает исследования [6, 7].
Постановка задачи
Рассмотрим 2П-вариант задачи. Будем считать, что жидкость является ньютоновской высоковязкой неоднородной и несжимаемой, а ее движение является изотермическим и стационарным. В случае высокой вязкости и (или) малой скорости движения жидкости число Рейнольдса для такого течения можно считать равным нулю. Таким образом, в ряде случаев уравнение Стокса можно принять в качестве основного при моделировании движения такой жидкости [8, 9]. В безразмерном виде уравнения движения имеют вид
Q: V«(ц (Vu + VuT)) = Vp + pe2, V*u = 0, (1)
где x gQ - пространственная координата; u = (u 1 (x); u 2(x)) - скорость жидкости; p = p (x) -давление; ц = ц ( x ) - вязкость; p = p ( x ) - плотность; e2 = (0,1) - единичный вектор; T - транспонирование тензора; (•,•) - скалярное произведение в R2; V - градиент; V* - дивергенция.
На границе Г = Г о иГ 1 0Г 2 иГ э рассматриваются граничные условия (см. рис. 1)
Г 0 : p = 0, ^ (u)= ц ( V u + V u T ) = 0, u = u0 ; Г 1 : (u,n) = 0 , ^ (u)n - ^ (u)n,n^n = 0 ; Г э :u = 0. (2)
Граница Г 0 свободна и на ней измеряется скорость движения жидкости u0. На границе Г 1 задано условие симметрии. На границе Г 2 жидкость втекает с известными плотностью и вязкостью, но скорость ее втекания неизвестна. На границе Г э задано условие прилипания.
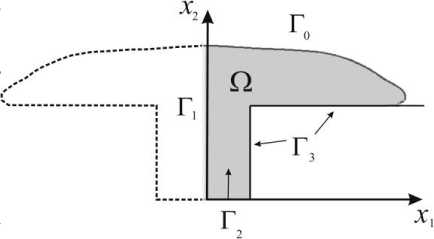
Обратная задача состоит в том, чтобы по результатам измерения скорости движения жидкости на свободной поверхности Г 0 найти скорость втекания
Рис. 1. Модельная область и ее граница жидкости на границе Г2 и поле скоростей движения жидкости в Q, т. е. требуется найти решение задачи (1), (2).
Задача (1), (2), вообще говоря, не обладает свойством устойчивости [4-7] по отношению к возмущению измеряемой скорости u0 , для ее решения требуются специальные методы.
Наряду с задачей (1), (2) рассмотрим вспомогательную задачу граничного управления, которую будем называть прямой задачей. Она в области Q описывается уравнениями (1) со следую щими граничными условиями:
Г 0: p = 0, ^ (u) = 0; F 1:(u,n) = 0 , ^ (u)n -( ^ (u)n,n)n = 0 ; Г 2:u = ^ ; Г э:u = 0. (3)
Вопросы корректности прямой и близких к ней задач обсуждались в [4, 5, 7, 8].
Метод решения обратной задачи
Для построения алгоритма решения задачи перейдём к вариационной постановке обратной задачи. Пусть наблюдаемая скорость движения жидкости u0 на Г 0 в обратной задаче соответствует некоторому заранее неизвестному распределению скорости (управляющему параметру) u = ^* на границе Г 2 в прямой задаче. Обозначим u* gQ решение задачи (1), (3) при заданном граничном условии u = ^* GГ 2 . Ясно, что u* = u0 на Г 0 . Рассмотрим функционал качества
I (9 = 111 u[^] - u 0 11^2 d Г ,
Г 0
Механика
где u[5] - решение прямой задачи (1), (3), где граничным условием Г 2 служит управляющее воздействие u = 5 . Данный функционал примет нулевое значение при 5 = 5* ( I (5*) = 0). Искомое граничное управление 5 * на Г 2 является минимизирующим элементом в вариационной задаче
I (5) ^ min: 5 g V . (4)
здесь V - некоторое множество допустимых управлений на Г 2 и элемент 5* g V .
От решения обратной задачи (1), (2) можно перейти к решению задачи (4). Для решения данной вариационной задачи применим итерационный метод градиентного спуска [10]. Для того чтобы придать вычислительному процессу большую устойчивость, добавим к функционалу качества регуляризирующую добавку (параметр регуляризации в > 0 выбирается эмпирически)
J (5) = I (5) + в Л Ц ||^ 2 d Г . (5)
Г 2
Минимизирующая последовательность в задаче (5) строится по правилу
5( П +1) = 5 ( П ) - Y ( П ) у J (5( п ) ), n = 1,2,3,... .
Шаг спуска вычисляется из скалярной задачи условной минимизации
J ( 5( П + 1) = 5( П ) - Y П ) v J (5( П ) ) ) ^ min : Y П ) > 0,
Y П )= j (5( П ) )| |v j (5( П ) )| Г*
L (Г 2 )
Градиент функционала определяется по правилу vJ(5) =vI(5) + 2в5 = (-qn + ^(W) n) I Г2 + 2в5 , где (w, q) - решение сопряженной краевой задачи
Q : v- ( ц ( v w + v w T ) ) = v q , v*w = 0 ,
Г 0: q = 0, ^ (w) n = 2 (u[5] - u 0 ); Г 1 :^ ,п^ = 0 , ^ (w)n - ^ (w)n,n^n = 0 ; Г 2:w = 0 ;
Г 3: w = 0.
Таким образом, последовательное решение прямой и сопряженной задач граничного управления позволяет аппроксимировать решение обратной задачи. При этом градиент функционала определяется аналитически. Затраты ресурсов ЭВМ на практике практически полностью состоят в качественном решении двух однотипных задач граничного управления для систем дифференциальных уравнений. Вопросы разрешимости таких задач исследованы в [3–5, 7, 10].
Численное моделирование
Для тестирования приведенного алгоритма были разработаны программные коды в пакете OpenFOAM [11]. Такой подход позволяет эффективно решать задачи механики сплошной среды в областях произвольной геометрии на современных вычислительных кластерах. Метод конечных объемов применялся для аппроксимации задач граничного управления. Тестовый пример рассчитывался на сетке из 104 гексаэдральных ячеек.
Расчетная область и исходные данные для решения обратной задачи определялись в пакете ANSYS Fluent [12] следующим образом. В области Q 1 с Ж2 рассматривается двухфазное ламинарное течение ньютоновской вязкой неоднородной несжимаемой жидкости в поле силы тяжести. Это движение описывается известными уравнениями Навье–Стокса [8]
d ( ^ u) + (u, v ( p u)) -v« ( ^ (u) ( v u + v u T ) ) = -v p - p g, x gQ 1 , t > 0;
u(0,x) = 0, x gQ 1 ; v* u = 0, x gQ 1 ;
перенос двухкомпонентной несжимаемой жидкости описывается уравнением
da _ _ . „ _ „
--+v*( a u) = 0 , a (0,x) = 0, x gQ1 , t > 0, S t
Короткий А.И., Реконструкция входящего потока вязкой жидкости по измерениям Цепелев И.А. скорости на доступном участке свободной поверхности течения плотность и вязкость среды может быть вычислена pt, x) = Pref (1 - a(t, x)) + pa(t, x), n(t, x) = ^ref (1 - a(t, x)) + n(x)a(t, x).
Здесь p ref = 10 - 4 Па^с; p ref = 1 кг/м3; n = 10 7 Па-с, P = 2500 кг/м3, h = 100 м. Тогда число Рейнольдса [9] в задаче примет значение ~10–4. Поэтому далее в моделировании жидкости мы отбрасываем инерционные члены в уравнении движения и переходим к уравнению Стокса. Функция a ( t , x) e [0,1] характеризует объемное задержание жидкости в момент времени t > 0 в точке пространства x eQ 1 . Область О определяется как объединение ячеек области Q 1 , в которых a ( t = 8000 5 ,x) > 0,99 (рис. 2).
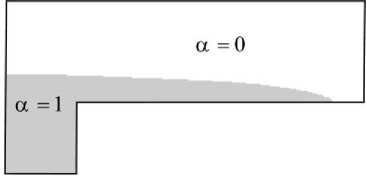
Рис. 2. Определение области Ω

Рис. 3. Тестовая функция для обратной задачи
На границе Г 2 заданы скорости по правилу ^* = 0,01(1 - X 1 )/ u * , X j e [0,1], и вычислены соответствующие скорости u0 на границе между жидкостью и воздухом (см. рис. 3). Эти распределения будут использованы в OpenFOAM для тестирования алгоритма. Параметр регуляризации в = 10 - 6, ^(0) = 0.

Рис. 4 . Погрешности восстановления скорости
На рис. 4 приведены погрешности восстановления поля скоростей u[^( n ) ] - u[^*] 2 при n = 0 (левый кадр) и n = 25 (правый кадр). Далее итерационный процесс не приводит к уменьшению погрешности восстановления. Оттенки серого цвета обозначают градацию относительной погрешности от 9 % до 300 %. Относительная погрешность в наихудшем случае составляет 9 % . Это связано с тем, что погрешности в исходных данных довольно большие. Более подробно данный вопрос для моделей механики высоковязкой жидкости изучен в работе [13].
Заключение
В работе предложен подход численного решения некорректной обратной граничной задачи об определении неизвестного распределения поля скоростей втекающей в некоторую область ньютоновской вязкой неоднородной несжимаемой жидкости по результатам измерения скорости движения жидкости на некоторой части границы области, на которой движение жидкости считается свободным. Развитие вычислительной техники, сочетание аналитических методов исследования систем дифференциальных уравнений, задач управления и устойчивых методов решения экстремальных задач позволяю решать сложные задачи механики сплошной среды. Проведены расчеты характерного примера обратной задачи. При численном моделировании был использован суперкомпьютер «Уран» ИММ УрО РАН.
Работа выполнена при поддержке Комплексной программы фундаментальных научных исследований УрО РАН (проект 18-1-1-8).
Механика
Список литературы Реконструкция входящего потока вязкой жидкости по измерениям скорости на доступном участке свободной поверхности течения
- Тихонов, А.Н. Методы решения некорректных задач / А.Н. Тихонов, В.Я. Арсенин. - М.: Наука, 1979. - 288 с.
- Иванов, В.К. Теория линейных некорректных задач и её приложения / В.К. Иванов, В.В. Васин, В.П. Танана. - М.: Наука, 1978. - 206 с.
- Самарский, А.А. Численные методы решения обратных задач математической физики / А.А. Самарский, П.Н. Вабищевич - М.: УРСС, 2004. - 480 с.
- Кабанихин, С.И. Обратные и некорректные задачи / С.И. Кабанихин. - Новосибирск: Сибирское научное издательство, 2009. - 457 с.
- Алексеев, Г.В. Анализ и оптимизация в гидродинамике вязкой жидкости / Г.В. Алексеев, Д.А. Терешко. - Владивосток: Дальнаука, 2008. - 364 с.
- Ismail-Zadeh, A. Data-Driven Numerical Modelling in Geodynamics: Methods and Applications / A. Ismail-Zadeh, A. Korotkii, I. Tsepelev. - Berlin: Springer International Publishing, 2016. - 105 p.
- Короткий, А.И. Моделирование прямых и обратных граничных задач для стационарных моделей тепломассопереноса / А.И. Короткий, Ю.В. Стародубцева. - Екатеринбург: Издательство Уральского университета, 2015. - 168 с.
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability / S. Chandrasekhar. - Oxford: Clarendon Press, 1961. - 652 p.
- Ландау, Л.Д. Гидродинамика / Л.Д. Ландау, Е.М. Лифшиц. - М.: Наука, 1986. - 736 с.
- Nocedal, J. Numerical Optimization / J. Nocedal, S.J. Wright. - New York: Springer, 1999. - 664 p.
- http://www.openfoam.org
- https://www.ansys.com/products/fluids/ansys-fluent
- Quantitative reconstruction of thermal and dynamic characteristics of volcanic lava from surface thermal measurements / A. Korotkii, D. Kovtunov, A. Ismail-Zadeh et al. // Geophysical Journal International. - 2016. - Vol. 205. - Issue 3. - P.1767-1779.


