Рекуррентная нейронная сеть TrackNETv3 для построения кандидатов в треки на эксперименте BM@N
Автор: Русов Даниил Игоревич, Никольская Анастасия Николаевна, Гончаров Павел Владимирович, Ососков Геннадий Алексеевич
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 3, 2021 года.
Бесплатный доступ
Работа посвящена разработке нейросетевого подхода для задачи реконструкции траекторий элементарных частиц. Данный подход был успешно реализован для данных Монте-Карло симуляции эксперимента BESIII в виде модели TrackNETv2. Однако, в силу особенностей GEM-детектора эксперимента BM@N, возникает ряд проблем. Предложены модификации нейросетевой модели TrackNETv2 для их решения, также внесены изменения в процесс обучения модели. На данный момент лучших результатов позволяют достичь полностью рекуррентная модель нейронной сети и сеть с использованием каузальной свертки. В результате тестирования лучшая модель показала эффективность распознавания треков, равную 0.9830. Также был оптимизирован процесс работы модели за счет использования библиотеки для быстрого поиска ближайших соседей Faiss.
Глубокое обучение, рекуррентные нейронные сети, реконструкция треков, GEM-детекторы, векторный поиск
Короткий адрес: https://sciup.org/14121838
IDR: 14121838 | УДК: 004.9, 004.93
Recurrent neural network TrackNETv3 for building of the track-candidates on the BM@N experiment
The work is devoted to the development of a neural network approach for the problem of track recon-struction. This approach is successfully used for Monte-Carlo simulation of the BESIII experiment in the form of TrackNETv2 model. However, due to the peculiarities of the GEM detector of the BM@N experi-ment, a number of problems arise. Modifications of the TrackNETv2 neural network model are proposed to solve them, and changes are also made to the training process of the model. At the moment, the best results are achieved by a fully recurrent neural network model and a network using causal convolution. As a result of testing, the best model showed the track efficiency equal to 0.9830. Also, the process of the model was optimized by using the Faiss library for efficient similarity search.
Текст научной статьи Рекуррентная нейронная сеть TrackNETv3 для построения кандидатов в треки на эксперименте BM@N
Rusov D., Nikolskaia A., Goncharov P., Ososkov G. Recurrent neural network TrackNETv3 for building of the track-candidates on the BM@N experiment, 2021;(3):17–29(In Russ). Available from:
Реконструкция траекторий элементарных частиц – это ключевая часть восстановления событий экспериментов физики высоких энергий. Цель задачи – группировка отдельных множеств зафиксированных точек пролета частиц (хитов) по критерию принадлежности какому-нибудь треку.
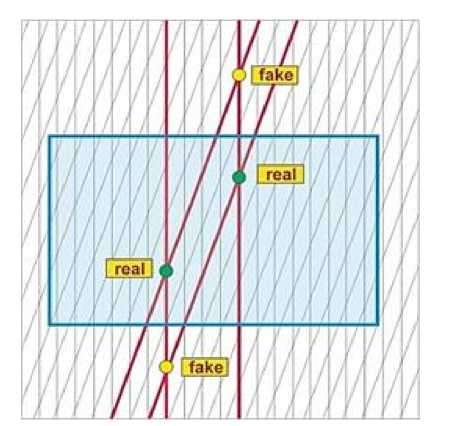
Решение данной задачи вызывает много трудностей. Например, расположение первичной вершины – точки взаимодействия частиц – во многих экспериментах неизвестно. В некоторых случаях треки различны по длине, из-за чего необходимо оценить, какая точка является последней. Также множество проблем связано с конструктивными особенностями установок, например, микрострипо-вый газовый электронный умножитель (ГЭУ) детектор образует большое количество ложных хитов, которые не относятся ни к одной частице (см. рис. 1).
real J
Рис. 1. Процесс рождения ложных стриповых пересечений – фейков. Стерео-угол между двумя стриповыми слоями позволяет убрать некоторое число фейков
К счастью, существует много классических алгоритмов с достаточной эффективностью решающих приведенные сложности, но большая их часть основана на фильтре Калмана, вызывает новые трудности. В современных условиях создается все больше экспериментов с высокой светимостью, которые создают огромные объемы данных. В результате классические алгоритмы не могут обеспечить приемлемую скорость обработки информации из-за низкого потенциала фильтра Калмана к масштабированию, параллелизации и высокой вычислительной сложности.
Это приводит к новому подходу к трекингу, использующему методы глубокого обучения. Модели нейронных сетей используются для нахождения сложных зависимостей в исходных данных в различных сферах. Преимущество данного способа заключается в большем потенциале для описания сложных зависимостей и преодолении проблем с вычислительной сложностью, так как все операции сводятся к последовательному умножению матриц, следовательно, легче распараллеливаются.
Такой подход был успешно реализован в некоторых работах, посвященных трекингу частиц в современных экспериментах. Например, графовая и рекуррентные нейронные сети показали высокую эффективность для данных Монте-Карло симуляции эксперимента BESIII [1].
В одной из моделей рекуррентной нейронной сети, TrackNETv 2 [2], объединены рекуррентные и сверточные слои для обнаружения пространственных зависимостей. В данной работе такой подход был изменен для более сложного сценария Монте-Карло симуляции эксперимента BM@N . Исследования показали, что различные длины треков частиц приводят к худшим результатам и значительному замедлению обучения. В качестве решения была в начале предложена процедура бакетинга (бакетинг (также биннинг) - техника обработки данных, когда исходный набор данных делится на некоторое количество интервалов, общее значение которых (обычно среднее) затем представляет все значения интервала, что позволяет уменьшить влияние отдельных наблюдений), используемая перед обучением.
Данная работа покажет, что подобный подход с применением бакетинга не следует использовать, потому что при разбиении настоящих треков модель может определить свойства, которые не соответствуют реальности. Другой проблемой является применение в старой модели ( TrackNETv2 ) сверточных слоев, в ходе работы которых для предсказания текущего хита использовалась информация о следующих точках. В связи с этим необходимы изменения в архитектуре модели и процессе обучения.
Процесс обучения
Подробное описание модели TrackNETv 2 было изложено в [2], но для ясности необходимо рассмотреть некоторые детали архитектуры для определения ее недостатков. На вход сети поступают координаты точек треков-кандидатов. Целью модели является предсказать центр и полуоси эллипса на следующей координатной плоскости, на которой производится поиск продолжения трека-кандидата. Следующей в данном случае называется станция после той, которой принадлежит последний хит в треке-кандидате. Если точки попали в эллипс, модель выбирает одну из них (обычно наиближайшую) и применяется повторно для предсказания эллипса на следующей станции, и так далее, пока не закончатся станции или трек-кандидат не выйдет за пределы области детектора. После построения трек-кандидатов производится фильтрация ложных треков при помощи классификатора. Модель TrackNETv 2 может быть рассмотрена, как нейросетевой аналог фильтра Калмана (ФК), за исключением этапа фитирования, выполняемого в ФК.
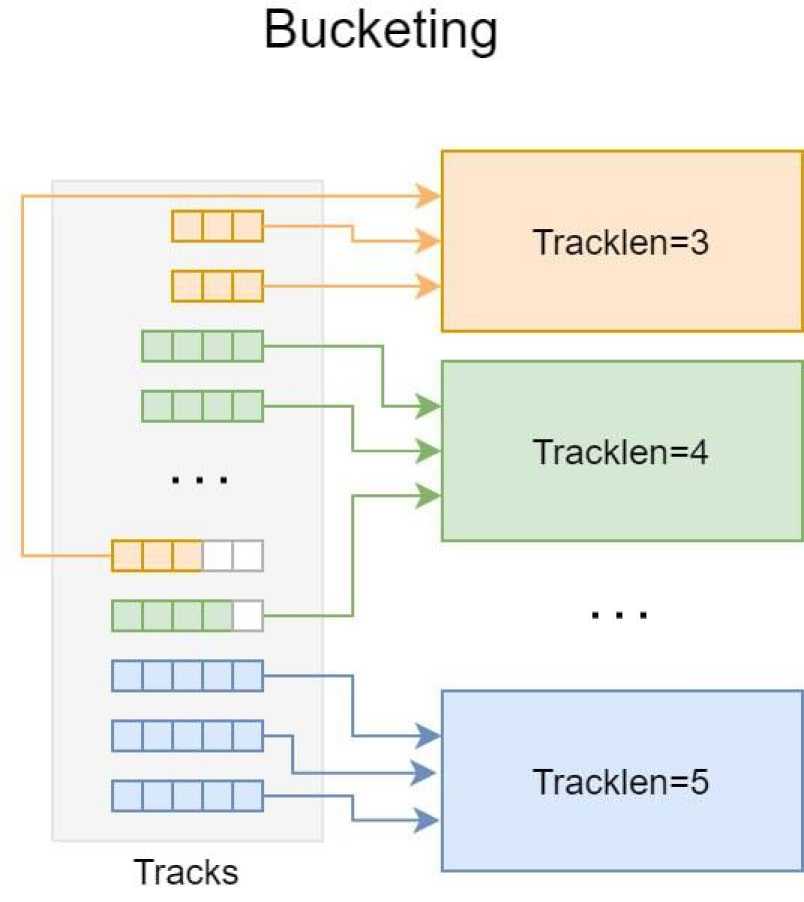
Первая версия TrackNETv 2 была обучена для задачи регрессии. На вход модели поступают хиты трек-кандидатов, целью является предсказание следующего хита на основе предыдущих. Треки состоят из различного количества хитов, поэтому для эффективного обучения была использована наша собственная версия процедуры бакетинга, отличная от общеизвестной (см. рис. 2). Треки сортируются по длине. Каждая группа треков с определенным числом хитов переформируются для балансировки размера всех групп. Случайно выбранные треки большой длины разбиваются и добавляются в набор к трекам меньшей длины. Таким образом создаются «бакеты» треков разной длины - от 3 до числа станций детектора. Затем последние точки в каждом треке выбираются как целевые значения предсказания и вычисления функции ошибки модели, все остальные хиты составляют входные данные.
Bucketing
Tracks
Tracklen=5
Tracklen=3
Tracklen=4
Рис. 2. Процедура бакетинга
Такой метод обучения является неестественным для рекуррентных нейронных сетей, даже если не принимать в расчет необходимость балансировки бакетов. Было принято решение переработать процедуру обучения, и предложен новый алгоритм. Для начала, полученные в результате Монте-Карло моделирования настоящие треки без последней точки подаются на вход модели. В то же время, все хиты кроме первого являются целевыми для вычисления функции ошибки. Модель учится делать предсказания для каждой точки, т. е. для первого хита производится предсказание координат второго хита, для двух точек ведется поиск третьей, и так далее. Таким образом, предсказание и вычисление функции ошибки делаются для каждого временного шага. Далее значение ошибки усредняется по всем отметкам времени и производится обратное распространение ошибки. Такой процесс обучения называется «многие ко многим».
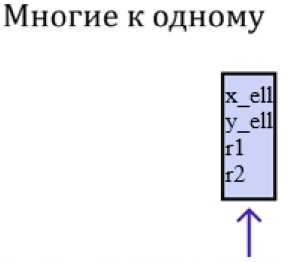
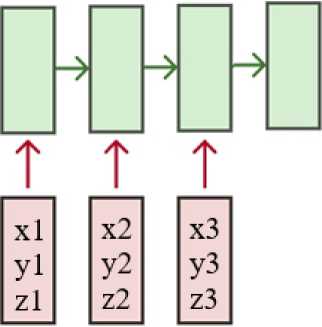
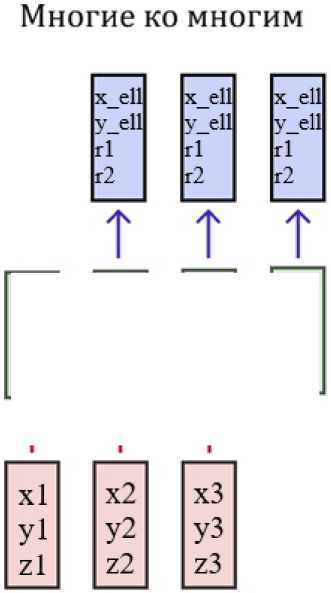
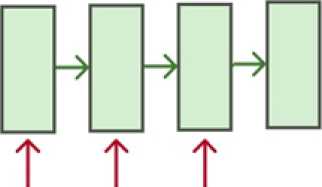
Рис. 3. Стратегия «Многие ко многим»
В одном батче входных данных могут присутствовать треки разной длины, поэтому необходимо дополнить более короткие элементы до наибольшей длины в батче. Обычно эта операция производится с использованием значения 0, поэтому если батч содержит два образца длины 4 и 6, кандидат с 4 хитами будет продлен двумя хитами, все координаты которых будут нулевыми (см. рис. 4). Во время оценки ошибки вычисляется специальная маска, данные шаги исключаются из процесса оптимизации.
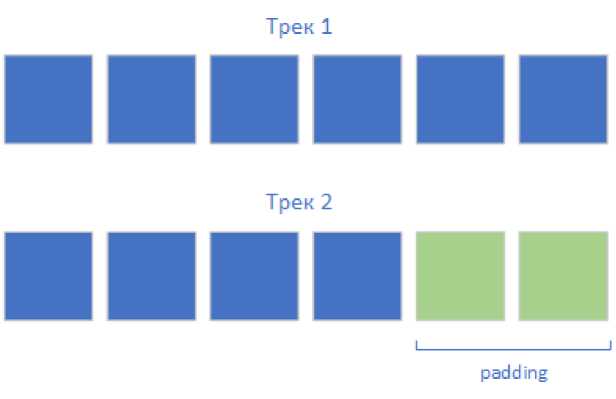
Рис. 4. Обработка треков разной длины
Улучшенная модель была названа TrackNETv 3, чтоб подчеркнуть отличия от предыдущей версии.
Каузальность как следствие
Модель TrackNETv 2 использует сверточный блок для того, чтоб повысить число входных параметров для рекуррентного слоя. Значение размера сверточного ядра модели выбрано 3. Для такого значения и паддинга ‘ same ’ (в данном случае 1), модель будет «заглядывать в будущее» на один шаг. Таким образом, если поставлена задача обучения модели с использованием стратегии “многие ко многим” (см. рис. 3), обычная операция свертки будет приводить к некорректному поведению модели при обучении.
Из всего этого можно сделать вывод, что модель должна быть каузальной, т. е. делать предсказания только на основе текущего и предыдущих временных шагов. Есть несколько путей к достижению этого. Первый, самый простой, убрать сверточный слой, сделав модель полностью рекуррентной. Забегая вперед, заметим, что данный подход позволил нам достичь лучших результатов. Следующий способ - изменить обычную операцию свертки на каузальную [3]. Каузальная свертка не позволяет модели нарушить порядок моделирования данных.
Еще одним вариантом модификации для улучшения модели является изменение рекуррентного блока на каузальные свертки, т. е. построение полностью сверточной сети - данный эксперимент оставлен для будущего исследования. Последняя опция - создание нейросетевой модели-трансформера [4]. с треугольной маской внимания. Трансформер - модель, основным преимуществом которой являются блоки самовнимания ( self-attention ). Такие модели широко используются во многих задачах от поиска ответов на вопросы [5] до классификации изображений [6]. Однако исследования, проведенные во время опубликования данной статьи, показали, что при помощи модели-трансформера не удалось получить результат,удовлетворительный по эффективности трекинга. Поэтому далее будет приведено сравнение двух моделей - полностью рекуррентной ( OnlyRNN) и модели с использованием каузального сверточного блока ( CNNRNN).
Оптимизация процесса работы модели
В ходе работы модели TrackNETv 2 требовалось проверить все хиты на соответствующей станции на попадание в предсказанные эллипсы, для чего необходимо выполнить перебор со сложность порядка O ( n Л2). Кроме того, для получения входных значений в последующем процессе инференса (тестирования работы обученной модели на конкретных данных) приходится использовать все возможные комбинации хитов на первых двух станциях, что также является излишним, и также приводит к квадратичной вычислительной сложности. С учетом этих недостатков процесса инференса предлагаются следующие шаги по его оптимизации.
Во-первых, есть возможность отказаться от использования всех сочетаний хитов на первых двух станциях как входных значений. Новая процедура обучения позволяет проводить предсказания, начиная с первой точки трека-кандидата. Данные уже содержат закономерности, необходимые для грубой оценки эллипса на основе первого хита. Размер эллипса будет значительным, но меньше размера целой станции.
Во-вторых, необходим быстрый поиск хитов, попавших в предсказанный эллипс. Существует библиотека для эффективного поиска и кластеризации векторов - Faiss [7]. Все хиты события помещаются в индекс, реализованный в Faiss. После того, как модель предсказывает эллипсы, на основе их центров производится поиск K ближайших соседей по их индексам. Только для этих точек проверяется попадание в эллипс. В итоге треки-кандидаты продлеваются подходящими точками и подаются на вход модели вновь. Поиск продолжения для треков-кандидатов производится с вычислительной сложностью порядка O ( NK) , где K << N .
Эксперименты
В первой части этого раздела приведены результаты валидации TrackNETv 3. Приведено сравнение различных наборов данных, параметров функции ошибки, оптимизаторов и моделей для выбора лучшего варианта. В следующей части рассматриваются результаты тестирования модели на новых данных.
Для валидации модели одновременно используются две метрики - полнота по хитам и площадь эллипса. Полнота определяется как доля хитов, попавших в эллипс, предсказанный моделью. Ее значение должно стремиться к единице, а площадь эллипса, наоборот, должна быть как можно меньше. Необходимо найти компромисс между двумя метриками, сохраняя полноту около 0.99.
Первая часть посвящена сравнению различных вариантов подготовки тренировочных данных для модели. Для обучения, валидации и оценки модели были использованы данные Монте-Карло моделирования 7-го запуска эксперимента BM@N [8]. Были сгенерированы около 750 тысяч событий для обучения и валидации модели. Использовались события с энергией пучка, равной 3.2 ГэВ. Рассматривались взаимодействия пучка аргона с мишенью из свинца ( ArPb ). Сила тока на магните была установлена в 1250 А. Мишень сгенерирована со следующими параметрами: X (среднее: 0.7 см, дисперсия: 0.33 см), Y (среднее: -3.7 см, дисперсия: 0.33 см) Z (центр: -1.1 см, толщина: 0.25 см). Седьмой запуск проводится с использованием 3 кремниевых станций и 6 ГЭУ, т. е. 9 станций в сумме. Количество треков в событии может доходить до 100, в среднем 37 треков в событии. На каждой станции может быть зафиксировано более 500 хитов, около 90% из них фейковые (см. рис. 5). Для наших экспериментов были созданы три набора данных – “ balanced ”, “ unbalanced ” и “ normalized ”. В “ balanced ” наборе была произведена балансировка размера групп треков разной длины. “ Unbalanced ” набор данных – это обработанная версия исходных данных, может рассматриваться как оригинальный набор данных. Для последнего, “ normalized ” набора, помимо балансировки, была проведена процедура нормализации на основе характеристик области детектора.
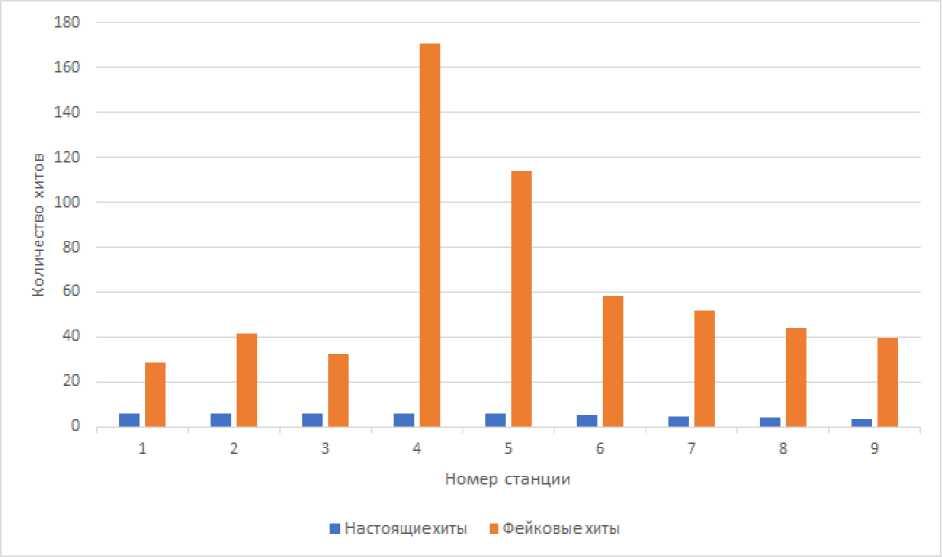
Рис. 5. Распределение количества хитов на станциях
Дополнительно были проведены эксперименты с изменением параметра альфа-функции ошибки, определяющим значение весов центра эллипса и его площади в вычислении значения функции ошибки. Оптимальное значение для «нормализованного» набора данных должно быть намного меньше, иначе предсказанные эллипсы будут иметь слишком большую площадь. На рисунке 6a можно увидеть, что модель, обученная с использованием “ unbalanced ” набора данных со значением альфа 0.95 показывает чуть лучший результат, но данные графики не иллюстрируют значения площади эллипса, что также имеет сильное влияние на качество результатов модели. Площадь эллипса относительно размера станций для модели с использованием «нормализованного» набора данных ниже, поэтому был выбран именно «нормализованный» набор данных.
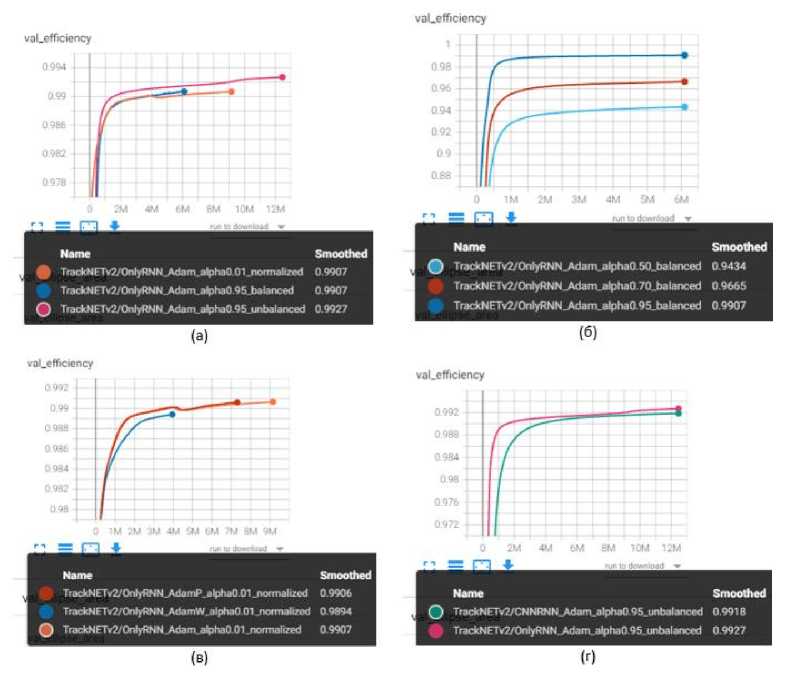
Рис. 6. Результаты валидации полноты по хитам на различных шагах процесса обучения.
a) Сравнение различных наборов данных. б) Сравнение различных значений параметра функции ошибки для “сбалансированного” набора данных. в) Сравнение различных оптимизаторов.
г) Сравнение различных видов моделей
Рисунок 6в показывает сравнение между разными оптимизаторами – Adam , AdamW и AdamP [9]. Обучение при помощи оптимизатора Adam проведено на большем количестве эпох обучения, чем с другими, тем не менее результаты Adam совпадают или лучше, чем с AdamW или AdamP , также Adam показывает лучшие результаты в плане скорости работы.
Также были использованы два вида моделей – с использованием сверточной части ( CNNRNN ) и без нее ( OnlyRNN ). График 6г показывает полноту по хитам. Модель OnlyRNN имеет немного лучшее значение данной метрики. Сравнивая площадь эллипсов, можно определить, что OnlyRNN со значением в 3.947 значительно лучше, чем CNNRNN со значением в 4.678.
Таким образом, лучшей комбинацией модель – набор данных – оптимизатор – альфа является OnlyRNN , обученная с использованием «нормализованного» набора данных, оптимизатора Adam и значения параметра функции ошибки 0.01.
Число ближайших соседей К является параметром и играет значительную роль: поиск с небольшими значениями ближайших соседей приводит к меньшему значению эффективности, но выполняется быстрее, большее количество ближайших соседей увеличивает эффективность, замедляя работу модели. Нами было установлено, что 5 ближайших соседей являются оптимальным значением для обеспечения компромисса по эффективности и скорости.
Табл. 1. Сравнение значений метрик моделей
|
Модель |
OnlyRNN, alpha 0.01, normalized |
CNNRNN, alpha 0.01, normalized |
OnlyRNN, alpha 0.95, unbalanced |
|
Полнота (по трекам) |
0.9830 |
0.9821 |
0.9778 |
|
Точность (по трекам) |
0.0209 |
0.0082 |
0.0072 |
Для оценки результатов модели используются две метрики - полнота и точность. Полнота – это доля треков, для которых более 70% хитов были восстановлены правильно. Точность – доля настоящих треков среди всех треков, распознанных моделью. Точность также является дополнением до единицы для доли ложных треков, называемых обычно «гостами» ( ghosts ). Метрики были вычислены на 2000 событий, результаты лучшей модели составили: полнота – 0.9830, точность – 0.0209 (см. рис. 7, 8).
На обработку одного события с использованием Intel ( R ) Xeon ( R ) Gold 6148 CPU @ 2.40 GHz в среднем требуется 2.2 секунды, дисперсия 3.7 с для версии программы, реализованной на языке Python . Такой большой разброс по времени выполнения объясняется тем, что в некоторых событиях может формироваться до нескольких сотен тысяч треков-кандидатов, которые модель TrackNETv 3 должна обработать.
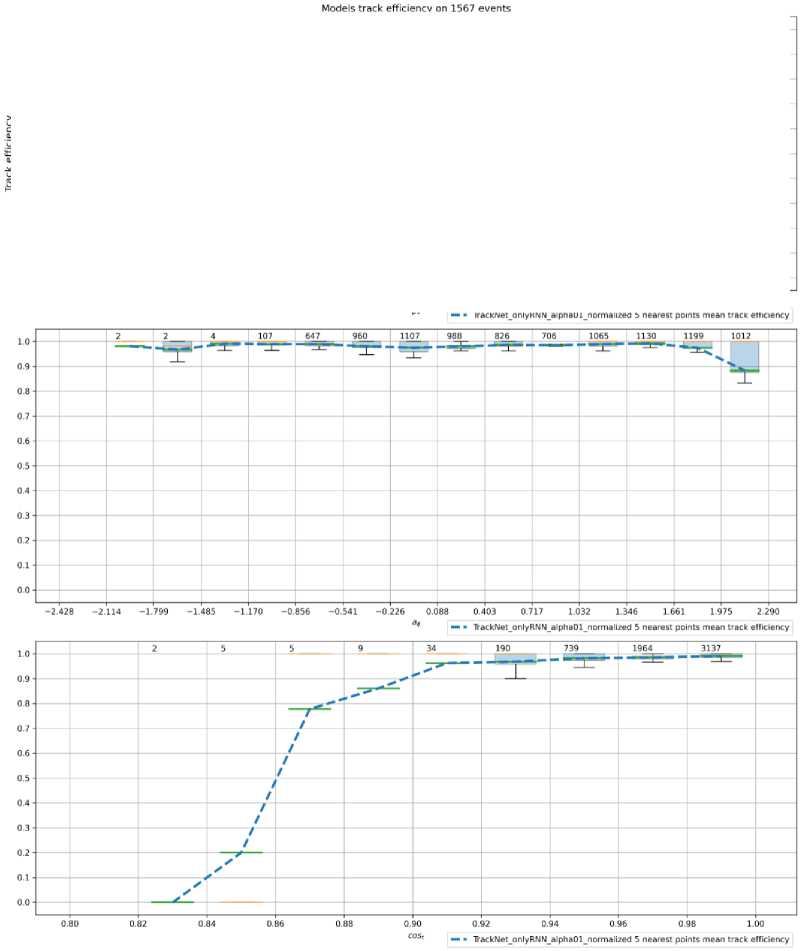
Рис. 7. Графики зависимости значения полноты от поперечного импульса, азимутального угла и косинуса полярного угла вылета (сверху вниз)
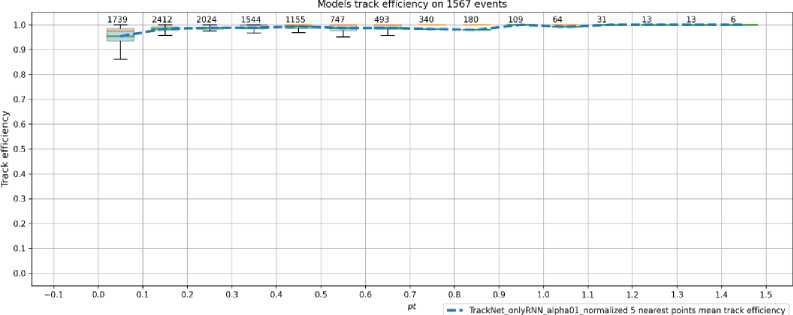
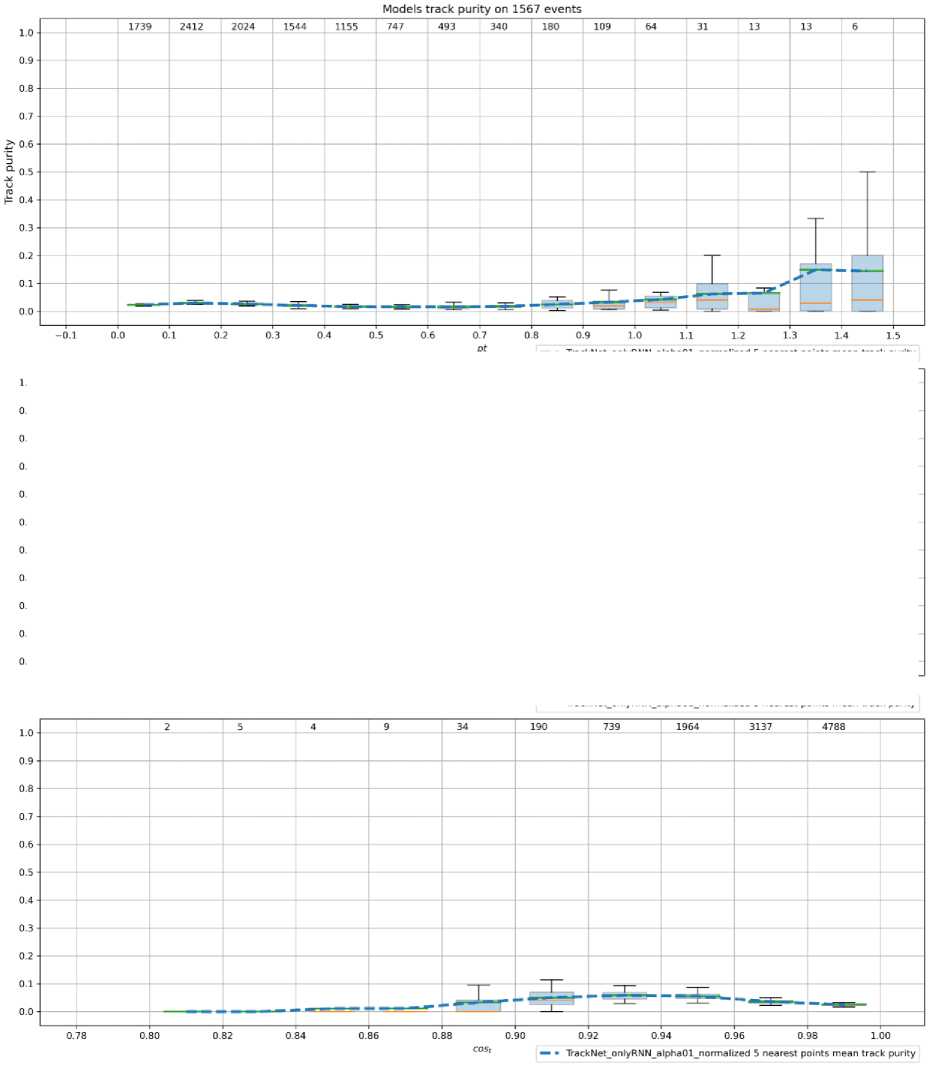
Рис. 8. Графики зависимости значения точности от поперечного импульса, азимутального угла и косинуса полярного угла вылета (сверху вниз)
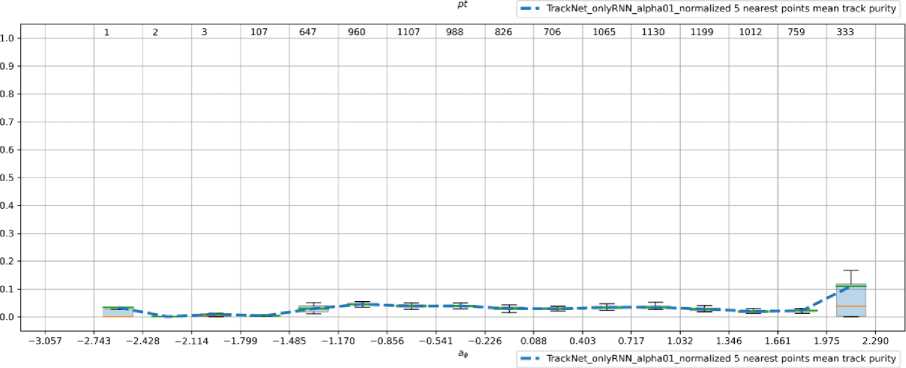
На графиках представлены зависимости полноты и точности (ось Y на рисунке 7 и 8, соответственно) от трех величин (сверху вниз): поперечный импульс Pt , азимутальный угол phi , косинус полярного угла вылета cos ( theta ) (см. формулу 1).

l)Pt = ^P? +Py 2)COS(<9) = = ----
^p2 + p2 + p2
3)0 = atan2(ipx,Py), где px, py, pz - импульсы трека по каждому из трех измерений
Формула 1. 1) Поперечный импульс; 2) Азимутальный угол; 3) Косинус полярного угла вылета
Значение метрики точности модели оставляет желать лучшего. Данную проблему можно решить путем разработки классификатора треков для дополнительной фильтрации гостов. Такой подход был реализован для данных эксперимента BESIII [10]. Однако, следует уточнить, что детектор BESIII устроен таким образом, что координаты X и Y первичной вершины события известны с достаточной точностью. Первичная вершина - это точка столкновения взаимодействующих частиц, т. е. все истинные треки должны вылетать из нее. Благодаря данной особенности появляется возможность использовать локальный классификатор треков. В случае эксперимента BM@N точных данных о положении первичной вершины нет, поэтому необходим классификатор, учитывающий ее местоположение, либо производящий классификацию сразу по всем трекам-кандидатам, т. е. учитывающий глобальную картину события. Таким классификатором потенциально может стать модель графовой нейронной сети [11].
Заключение
Нами был переработан подход к обучению и оптимизирован процесс работы нейросетевой модели TrackNETv 3 с целью снижения алгоритмической сложности. Новая модель достигает полноты в 0.9830 и точности в 0.0209 для данных Монте-Карло моделирования седьмого запуска эксперимента BM@N . Классификатор треков-кандидатов, используемый для фильтрации фейковых треков и повышения точности, будет разработан в будущем. Скорость обработки одного события с использованием процессора Intel ( R ) Xeon ( R ) Gold 6148 CPU @ 2.40 GHz в среднем составляет 2.2 секунды.
Все эксперименты были проведены с использованием инструментов библиотеки Ariadne [12].
Расчеты проводились при помощи гетерогенной вычислительной платформы HybriLIT (ЛИТ, ОИЯИ) [13].
Исследование выполнено за счет гранта РФФИ, проект № 18-02-40101.
Список литературы Рекуррентная нейронная сеть TrackNETv3 для построения кандидатов в треки на эксперименте BM@N
- Ососков Г. А. и др. Нейросетевая реконструкция треков частиц для внутреннего CGEM-детектора эксперимента BESIII / Г.А. Ососков, О.В. Бакина, Д.А. Баранов, П.В. Гончаров, И.И. Денисенко, А.С. Жемчугов, Ю.А. Нефедов, А.В. Нечаевский, А.Н. Никольская, E.M. Щавелев, Л. Ван, Ш. Сунь, Я.Чжан // Компьютерные исследования и моделирование. — 2020. — Т. 12. — №. 6. — С. 1361–1381.
- Goncharov P. Particle track reconstruction with the TrackNETv2 / Р. Goncharov, G. Ososkov, D. Bara-nov //AIP Conference Proceedings. — AIP Publishing LLC, 2019. — Vol. 2163. — No. 1. — P. 040003.
- Oord A. et al. Wavenet: A generative model for raw audio //arXiv preprint arXiv:1609.03499. — 2016.
- Vaswani A. et al. Attention is all you need //Advances in neural information processing systems. — 2017. — С. 5998–6008.
- Devlin J. et al. Bert: Pre-training of deep bidirectional transformers for language understanding //arXiv preprint arXiv:1810.04805. — 2018.
- Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., et al. An image is worth 16x16 words: Transformers for image recognition at scale. In Proceedings of International Conference on Learning Representations (ICLR), 2021.
- Johnson J., Douze M., Jégou H. Billion-scale similarity search with gpus //IEEE Transactions on Big Data. — 2019.
- Kapishin M. et al. Studies of baryonic matter at the BM@ N experiment (JINR) //Nuclear Physics A. – 2019. — Vol. 982. — Pp. 967–970.
- Heo B. et al. AdamP: Slowing down the slowdown for momentum optimizers on scale-invariant weights //arXiv preprint arXiv:2006.08217. — 2020.
- Nikolskaia A. et al. Local strategy of particle tracking with TrackNETv2 on the BES-III CGEM inner detector / A. Nikolskaia, E. Schavelev, P. Goncharov, G. Ososkov, Y. Nefedov, A. Zhemchugov and I. Denisenko //AIP Conference Proceedings. — AIP Publishing LLC, 2021. — Vol. 2377. — No. 1. — P. 060004.
- Bakina O. et al. Global strategy of tracking on the basis of graph neural network for BES-III CGEM inner detector / O. Bakina, I. Denisenko, P. Goncharov, Y. Nefedov, A. Nikolskaya, G. Ososkov, E. Shchavelev and A. Zhemchugov //AIP Conference Proceedings. — AIP Publishing LLC, 2021. — Vol. 2377. — No. 1. — P. 060001.
- Goncharov P. et al. Ariadne: PyTorch library for particle track reconstruction using deep learning / P. Goncharov, E. Schavelev, A. Nikolskaya, and G. Ososkov //AIP Conference Proceedings. — AIP Pub-lishing LLC, 2021. — Vol. 2377. — No. 1. — P. 040004.
- Adam G. et al. IT-ecosystem of the HybriLIT heterogeneous platform for high-performance computing and training of IT-specialists //English, in CEUR Workshop Proceedings, V. Korenkov, A. Nechaev-skiy, T. Zaikina, and E. Mazhitova, Eds. — 2018. — Vol. 2267. — Pp. 638–644.


