Relative Performance of Certain Meta Heuristics on Vehicle Routing Problem with Time Windows

Published Online November 2015 in MECS DOI: 10.5815/ijitcs.2015.12.05

In today’s competitive environment it is necessary to save critical resources. Transportation is one of the major modes of consumption of energy as it is used for transportation of goods between different locations. Moreover it also contributes to the global warming by emitting CO2. Therefore best possible utilization of transportation systems is key to reduction in energy consumption as well as global warming. One of the important problem and widely studied in operation research that deals with efficient routing and scheduling of fleets is Vehicle Routing Problem (VRP).

A typical VRP can be described as problem of finding least cost route between depot and customers in such a way that each customer is visited once and only once by identical capacity vehicles such that total demand on each route does not exceed the vehicle capacity. The objective of the problem is to minimize the total traveled distance and the number of vehicles used so that both operational and maintaince cost is reduced.

The Vehicle Routing Problem with Time Windows (VRPTW) is variant of VRP with additional complexity of serving each customer within its time windows. VRPTW arises in many real life scenarios like bank, hot meal, perishable food deliveries etc. The time window of a customer, i , is represented by [ e_i , l_i ] where e_i and l_i are the earliest and latest arrival time respectively. Service to a customer will be provided by a vehicle only if it arrives within this time period as shown in Fig 1 (a). A vehicle can arrive at customer location before its opening window but it has to wait till opening of window as shown in Fig 1 (b) but cannot after its closing window as shown in Fig 1 (c).

Fig. 1. (a)-(c) Time windows for customer i

VRP is generalization of famous combinatorial problem TSP with multiple vehicles. VRP is NP hard problem and it is one of the most difficult problem to solve in operation research. Many exact and meta heuristic approaches are applied to solve the problem but there exists no algorithm that guarantee to find optimal solution within a computational time. VRPTW is even more complex because of additional constraints. Even for instances with few customers and vehicles efficient routing is a difficult task. Solution space rapidly grows with a small increase in input size hence manual calculated routes are ineffective and human planner looks for automated planning tools to reduce the workload and time. Meta heuristics approaches which stand between exact and heuristic approaches are often tried for finding solutions to reach problems in reasonable time. Moreover they are also used for solving other problem too [26]. SA, GA, ACO, local searches, neural network, variable neighborhood search are some of the examples of meta heuristics. A review of application of neural network can be found in [27].

In this paper three basic meta heuristics namely Simulated Annealing (SA), Genetic (GA) and Ant Colony System (ACS) were implemented and analyzed using different parameters for different datasets by considering total travel distance as the primary objective to be minimized. The main contribution of this paper is that it provides a categorization of various meta heuristics for VRPTW and empirical analysis of three different meta heuristics on different parameters.

II.    Literature Review

A state of the art in the field of VRPTW with heuristic approach is discussed in [1]. In this state of art overview of various methods along with their comparison on different parameters are described. Various heuristic techniques for solution construction and solution improvement phase are discussed in [2]. A survey on the progress and evolution of the problem statement is presented in [3]. In this paper various possible algorithms with their pros and cons are discussed. A taxonomy review encompassing all of the managerial, physical, theoretical disciplines are presented in [4]. A parallel mimetic algorithm for VRPTW is proposed in [5]. In this algorithm genetic and some local refinement procedure are executed in parallel to find solution. For improving the results a novel ran doming scheme is developed by which process communication takes place. A Particle Swarm Optimization algorithm is proposed for solving VRPTW in [6]. Furthermore the proposed algorithm is validated on a real world case study of Chlorine Capsule Distribution Company to the water reservoir in Tehran. A two phase hybrid meta heuristic for VRPTW is presented in [7]. In this firstly variable neighborhood search is applied to minimize the number of routes and then in second phase total travelled distance is minimized using tabu search algorithm. All exchange, all -2-opt, all cross exchange and all relocate and ejection chain operators are designed. A genetic algorithm using an optimized cross over operator is used in [8] to find optimal solution for VRPTW. VRPTW is solved using GA and PSO in [9]. Both single and hybridization of both meta heuristics were implemented. It is concluded that PSO perform better for clustered problems and GA is better for random customer distribution. A review of exact heuristics and meta heuristics methods for solving VRPTW is surveyed in [10]. Mathematical analysis of various meta heuristics is discussed in [11]. In their work authors had provided an overview of convergence and efficiency studies of meta heuristics and provided a frame work for analyzing meta heuristics in term of convergence and efficiency. Open challenge for future work is also provided. In [12] two meta heuristics named SA and iterated local search are applied to solve the problem. Both algorithms use constructive heuristic and various operators and strategies for route improvement. Calculation results show an improvement in 44 instances of Solomon test data. Case study of postal service is also provided. In [13] a two phase method using GA and random search incorporating SA is implemented to solve VRPTW in various scenarios. A two stage ant colony optimization algorithm is proposed in [14]. The proposed two stage of algorithm have different goals and both are independent of each other. The objective of first goal is to minimize the number of vehicles and in the second stage the total distance is minimized using local search methods. In [15] a hybrid algorithm Gen SAT is proposed. In this algorithm initial solution is obtained using push forward insertion heuristic. Л — Interchange mechanism is proposed which moves customers between routes to generate neighborhood solutions for the VRPTW. Simulated annealing and tabu search is used for searching of Л — interchange. A hybridization of SA and ACO (IACS-SA) is proposed for solving VRPTW in [16]. The proposed algorithm combines the strength of both search heuristics. Moreover a new route construction rule, a new pheromone update rule and diverse local search approaches were proposed. In [17, 18] an enhanced ant colony system for solving VRPTW is applied in which other factors like urgency to serve, bias and wait factors were incorporated with distance in state transition rule.

Table 1. Approaches used in VRPTW

Authors’	Approach	Initial   Solution/Solution Construction	Solution Improvement/Operators
Ming yoa, QI et al.[7]	VNS and TS	Solomon I1 insertion	Exchange, 2 opt and Cross Exchange
H.Nazif, L.S.Lee[8]	GA	Random	Swap and insertion
Suraya Masorm[9]	GA and PSO	-	-
Bhawna Minocha and Saswati Tripathi[13]	GA and Random Search	Push  Forward  Insertion Heuristic	SA
Xudong Wu[14]	ACO	Solomon I1 insertion	Local Search
Sam R. Thangiah et al [15]	Hybrid (GA, SA,TS)	Push  Forward  Insertion Heuristic	2 -interchange
Chea-Ho  Chen  and ching-Jung Ting [16]	Hybrid (ACS and SA)	Nearest Neighbor	Local Search
Sandhya and V.Katiyar [17,18]	ACS	Nearest Neighbor	-
R. Banos et al.[21]	EA and SA	-	-
Phuong Khanh Nguyen [22]	Hybrid	Solomon I1 insertion	Local Search

Pheromone update is also done with a minimum and maximum upper bound. An overview along with recent advances in ACO is discussed in [19]. In paper they also discuss the extensions, applications of ACO and various issues related to ACO. A multi objective evolutionary algorithm (MOEA) that can minimize any number of objectives and a mechanism for more diversity is proposed in which 1st offspring is selected as usual in EA but other offspring’s are selected from non-common areas of the search space from the second parent [20]. A multi start evolutionary algorithm with SA is designed for solving VRPTW in [21] and tested on 100 customers of Solomon data set. In this paper populations are optimized using the mutation operators of usual EA and offspring’s individually are accepted or rejected by applying SA. Vidal et al. [22] developed a hybrid GA with adaptive diversity management for VRPTW and it was claimed to be the best meta heuristic. Proposed method combines the exploration of GA and local search for intensification. Permutation encoding without deliminators is used for individual representation. Finally a split procedure is used to partition solution for getting final tour. A general tool using tabu search is proposed for solving VRPTW in [23]. In their work the neighborhood structure is exponential in size resulting in evaluation procedure of polynomial complexity. Summarization of approaches used in VRPTW is given in Table 1.

III.    Metaheuristics for VRPTW

For solving optimization problem like VRPTW various methods are proposed in literature. Solving methods for VRPTW can be divided into 2 main categories as shown in Fig. 2

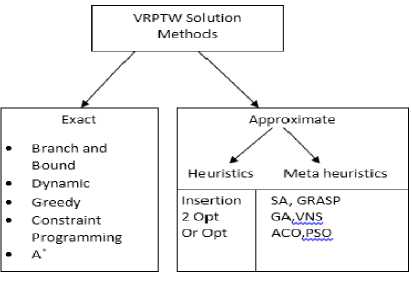
two contradictory criteria’s: Intensification (exploitation) and diversification (exploration). Balance between these 2 criteria’s is important for obtaining high quality solution by exploring all promising and non-promising areas and faster solution by exploring only promising areas. Various classification criteria’s can be used for classifying meta heuristics:

• 1.    Nature vs Non nature: Nature is the rich source of inspiration for many meta heuristics. Therefore almost all are nature inspired. Some of them are bio-inspired like GA, EA. Some are swarm inspired like ACO, PSO and other are from physics/chemistry based like SA. TS and DE are the example of former category.

• 2.    Memory vs memory less: Some meta heuristics which uses memory for information extraction during search history are memory based meta heuristics. Some popular examples are ACO, Tabu etc. On the other hand some SA, GA are memory less meta heuristics.

• 3.    Deterministic vs Stochastic: Stochastic meta heuristic solves optimization problems by applying random rules during their search process. The idea behind is to escape from local optima. On the other hand deterministic meta heuristics apply deterministic decisions to get some final solution by using the same initial solution.

• 4.    Population based vs Single solution based: Another important characteristic for classification of meta heuristic is the number of solution used at the same time. Single solution based meta heuristic like SA and local search manipulate a single solution while in population based meta heuristics a whole set of solution is evolved. Some examples of this category are ACO, GA.

• 5.    Trajectory vs multiple neighborhood moves: In trajectory method single neighborhood structure exists and it allows worse move to accept whereas in case of multiple neighborhood moves meta heuristics use a set of neighborhood structure.

• 6.    Attraction vs Non-attraction: In case of attraction based meta heuristics interaction of multiple agents takes place like in ACO. GA is the example of non- attraction meta heuristics.

• 7.    Rule vs Equation based: In rule base explicit updation of rules are used like GA.

Fig. 2. Solution Methods for VRPTW problem

Exact methods guarantees to find optimal solution if sufficient time and space is given. On the other hand heuristics are the techniques that can find a feasible solution with reasonable time. Heuristic does not guarantee about the solution quality although it can be made by empirical analysis. A popular class of approximate method is meta heuristics that are the general frame work for the heuristic methods. Meta heuristics provides acceptable solution within a reasonable time by iteratively improving the candidate solution. The design space of meta heuristic is based on

Table 2. Categorization of Meta heuristics on various parameters

Features	SA	TS	GA	ACO	GRASP
Trajectory	Y	Y	N	N	Y
Population	N	N	Y	Y	N
Memory	N	Y	P	Y	N
Multiple Neighborhood	N	N	P	N	Y
Dynamic	N	P	N	N	N
Nature Inspired	Y	N	Y	Y	N
Stochastic	Y	N	Y	Y	N

On these parameters various popular meta heuristics along with their properties are summarized in Table 2. Here Y denotes the presence of feature in the meta heuristic, N represent the absence of feature and P represents the partial presence of feature.

Among these SA, GA and ACO were chosen for comparison keeping in mind that all three are nature inspired and stochastic in nature. On the other hand GA and ACO possess some common properties that are different from SA like both are population based meta heuristics and uses memory for information extraction. A brief overview of these meta heuristic are given below in

Table 4.

IV.    Xperimental Results for VRPTW

In this paper we implemented SA, ACO and GA for solving VRPTW. Pseudo code for these three methods can be reviewed from [24]. These pseudo codes are implemented in MATLAB and executed on Windows 7 platform. After sensitive analysis values of various parameters used for these meta heuristics are given in Table 3.

Table 3. Value for various parameters

Parameters Meta heuristics	Population	Mutatio n Rate	Temp .	Coolin g Rate	Absolut e Temp.	a	p	Y	P
GA	1000	0.1
SA			10000	0.999	0.001
ACO						1	3	1	0.2

• A. Performance Metrics

For empirical analysis between implemented meta heuristics various factors were taken, their detail description are as follows:

• (a) Data set: In this paper 2 categories of problems are taken on the basis of time windows type 1 and type 2. Type 1 problems have short time windows whereas type 2 problems have long time windows. Further these 2 categories consist of three problems based on geographical distribution of customers namely Random(R), Clustered (C) and Random Clustered (RC). The geographical distributions of 100 customers for different problems are shown in Fig 3 (a) and Fig 3 (b). Here circle nodes represent the customers and depot is shown by square. The layout for C and RC problems are same i.e X ranges from [-40, 60] and Y ranges from [-50, 40] and for R problems range for X is[ -40,40] and Y ranges from [40,50]. Fig 3 (a) shows clear clusters of customers having 10 customers per cluster and Fig 3 (b) shows the random distribution of customers and similar picture can be obtained for random clustered problem in which clusters are formed at the boundaries and random distribution of customers at the center.

  

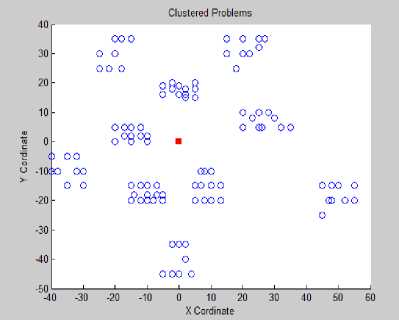
  (a) C class problem

  
  
  

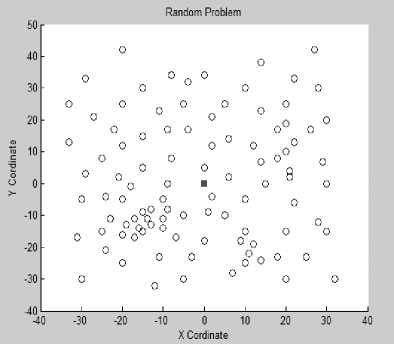
  (b) R class problem

  Fig. 3. (a), (b) Geographical Distribution of customers.

  
  

Table 4. Features of SA, GA, ACO

Features	ACO	GA	SA
Proposed By	Marco Dorigo	John Holland	Kirkpatrick, Gelatt and Vecchi
Inspiration Source	Food Searching Behavior of Ants	Evolution and natural Selection	Annealing in metallurgy
Working	1.    Initialize parameters. 2.    Repeat step 3 and 4 until stopping condition is met. 3.    Construct Solutions 4.    Update pheromone trails 5.    Output result.	1.  Generate populations and fitness function. 2.    Evaluate population. 3.  Repeat  following  until  stopping condition is met. (a)    Crossover (b)    Mutation (c ) Evaluate 4.    Output result.	1.    Initialize     temperature     and generate initial solution. 2.    Repeat step 3 and 4 until stopping condition is met. 3.  Generate new solution by making change to current solution. 4. Accept  solution with  some probability. 5.  Output result.
Advantages	1.    Distributed Computing 2.    Performance does not relies on initial solution. 3.    Retains knowledge of good solution. 4.    Robust and can be hybridized with other algorithms. 5.    Best suited for problems which are dynamic in nature.	1.    Performance does not relies on initial solution. 2.    Best   solution   but   high   time computation. 3.    Applicable for multiobjective problems. 4.    Best suited for problems having no mathematical analysis.	1.    Easy to code for complex problems. 2.    Can  handle  problems  having unordered   data   and   many constraints. 3.    Statically guarantees to find global optimal solution.
Disadvantages	1.    Pheromone stagnation results in premature convergence. 2.    Ant communication mechanism is time consuming.	1.    Knowledge of good solutions can be destroyed by operators. 2.    Difficult to apply for dynamic and highly constraint problems.	1.  Performance relies on initial solution. 2.  Continuous annealing is time consuming. 3.    Tradeoff between solution quality and time consumption.

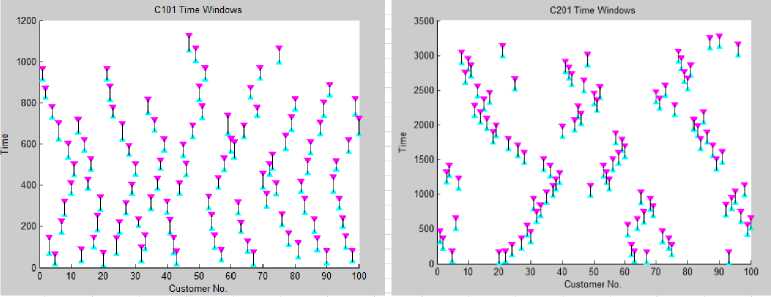
Fig. 4. (a) and (b)

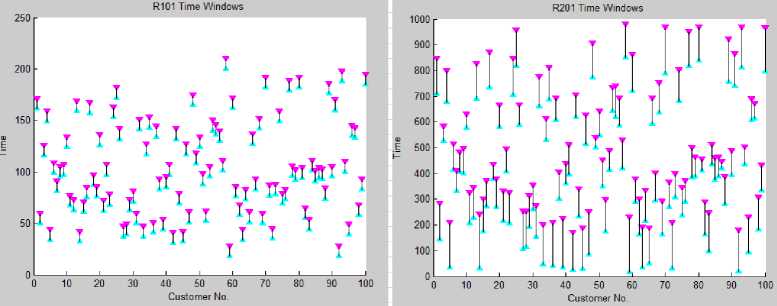
Fig. 4. (c) and (d)

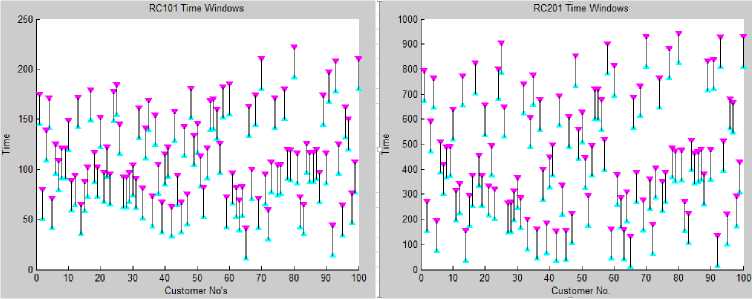
Fig. 4. (e) and (f)

Fig 4 (a) and (b) represents the characteristic of time windows for C1 problem and C2 problem. Fig 4 (c) and (d) represents the characteristics of time windows for R1 and R2 problem while fig 4 (e) and (f) shows for RC1 and RC2 problems. In all three cases X axis represents the customer number and Y axis denotes the time. Vertical bar represents the time windows.

Table 5 shows the results obtained for problems with 25, 50 and 100 customers respectively.

Table 5. Total travelled distance and CPU time for 25, 50, 100 customers

No. of Customers		Initial Solution		SA		GA		ACO
25	Problem	TD	Time (sec)	TD	Time (sec)	TD	Time (sec)	TD	Time (sec)
	R1	2464.7	.5	451.5	71	429.6	210	427.8	137
	C1	2459.1	.3	198.2	484.6	191.3	187.7	191.3	115
	RC1	3419.1	.3	342.3	67.6	351.5	193.8	342.3	56
	R2	3384.7	.3	456.5	56	417	365.2	417	71
	C2	2140.3	.3	461	164	410	368	410	267
	RC2	4251.6	.3	315.7	58	301.5	226.1	301.5	54
50	R1	2648.5	1	772.2	367.2	694.7	1028	696.3	872
	C1	2483.0	1	401.2	484.6	398.7	936.1	327	295
	RC1	3523.8	1	685.95	150.3	669.2	806.4	677.8	121
	R2	3604.9	1	639.1	258	581.5	1544.14	573.7	783
	C2	2363.6	1	717.4	993.5	751.3	1549.7	720.1	873
	RC2	4495.3	1	665.3	554.8	588	2239.7	587.7	623
100	R1	2550.6	7	1215.8	2433.5	1198	2962	1201.7	2347
	C1	2310.0	6	968.7	2461.3	873.5	2993.3	828.9	582
	RC1	3307.6	6	1442.7	1132.4	1308.5	3550.2	1308.5	2107
	R2	3592.8	6	962.2	2100	1154	5206.4	962.2	2154
	C2	3572.3	6	1261.6	4447.5	1362.4	6114	1261.6	4232
	RC2	4778.3	6	1165	2375.4	1138	8875	1143.9	2884

(b) Improvement in total distance: Improvement in           is summarized for three metaheuristics for total travel distance means how much results are           customers in table 6. optimized after applying meta heuristics. In this paper initial solution is obtained by nearest               Improvement = TD v"v -TD Metaheur t st t c * 100 neighbor and saving is calculated as follows and                                    tdnn Table 6. Improvement in total distance for 25, 50, 100 customers																			100 (1)
Problem	R1			C1			RC1			R2			C2			RC2
No.      of Customers	25	50	100	25	50	100	25	50	100	25	50	100	25	50	100	25	50	100
Meta heuristics	% of Improvement
SA	82	71	52	92	84	58	90	81	56	87	82	73	78	70	65	93	85	76
GA	83	74	53	92	84	62	90	81	60	88	84	68	81	68	62	93	87	76
ACO	83	74	53	92	87	64	90	81	60	88	84	73	81	70	65	93	87	76

It can be obtained from the above table that the % of improvement is high for small size problems and it worsen as the problem size increases because the number of possible permutation increases exponentially. All meta heuristics performs well for different problems but the % of improvement is high for ACO when compared with SA and GA.

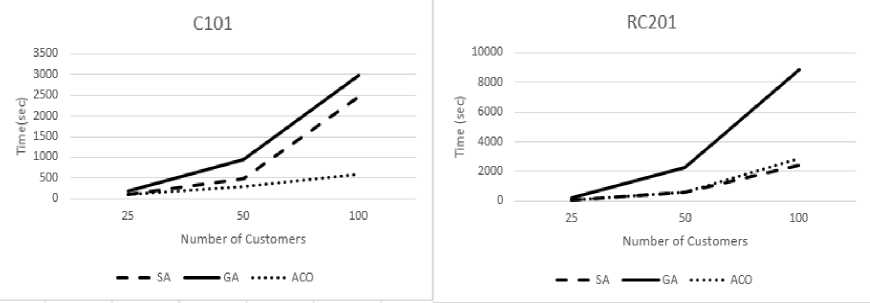
• (c)    Time Complexity: Time complexity of the algorithm is calculated in terms of CPU time taken by the meta to run to its execution. In this paper time is measured in seconds and is shown in fig 5 (a)-(f) for different instances. Three

observations can be made that (i) time complexity grows with the size of input and (ii) GA is the most time consuming meta heuristic (iii) SA gives good solutions in faster run time.

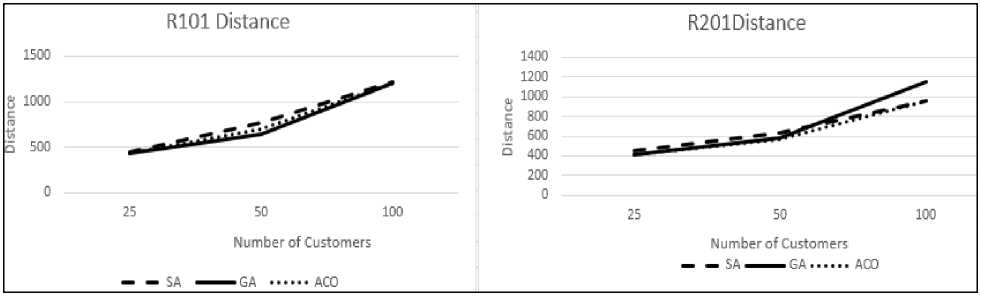
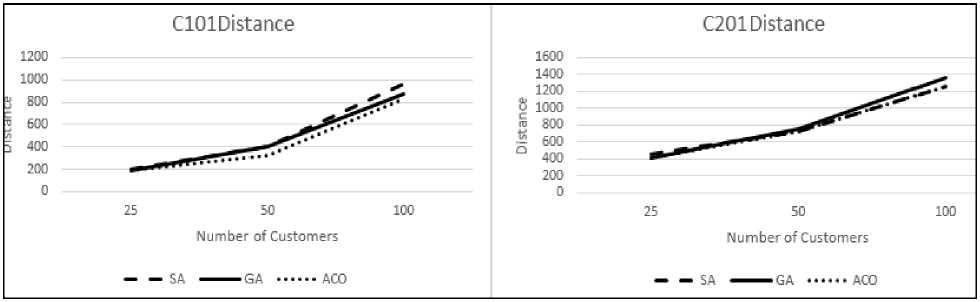
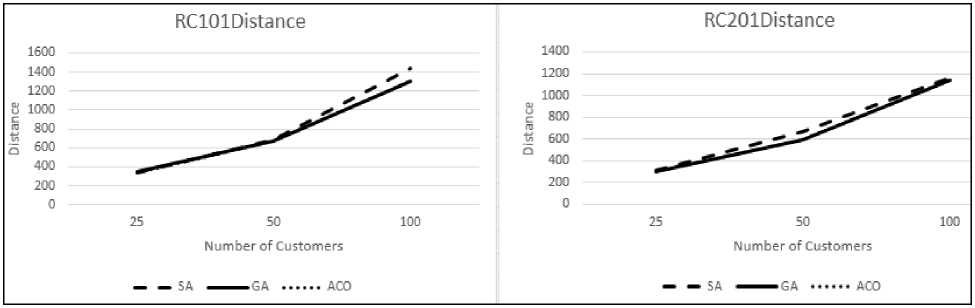
• (d)    Solution quality: Solution quality is measured in terms of total travel distance. Less distance represents the high quality solution while high travel distance means comparatively less quality solution. From fig 6 (a)-(f) it can be concluded that solution quality is good for small size problems but it reduces as the size increases. For large size problems solution quality provided by GA is better that SA and ACO.

  

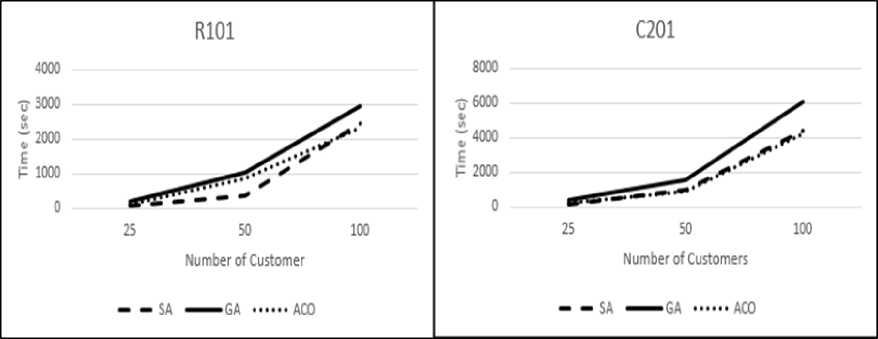
  (a) R101                                                  (b) C201

  
  
  

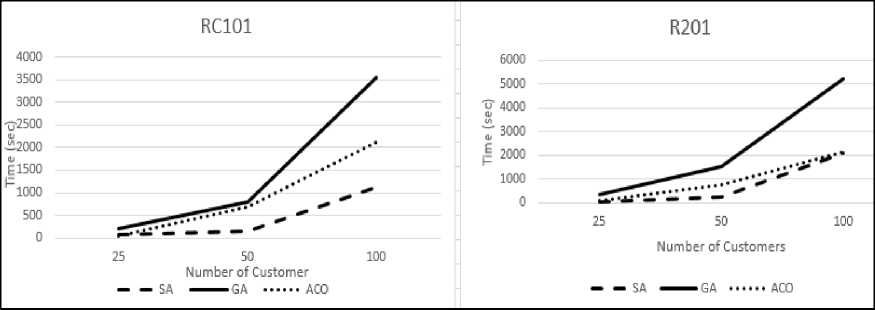
  (c) RC101                                               (d) R201

  
  
  

  (e) C101

  (f) RC201

  Fig. 5. Time complexity for instance

  
  

• (e)    Robustness:  Robustness means how the

performance of meta heuristics changes if some input parameter is changed. A robust algorithm should perform consistently over wide variety of problems and should not be sensitive to changes in input size. In this paper numbers of customers are varied from 25, 50 and 100 to check the robustness of meta heuristics. It can be observed from table 4.2 (a)-(c) that ACO and GA provides robust results for all three cases but the robustness for SA degrades with the increase in number of customers.

• (f)    Simplicity: Simplicity refers to ease of coding. Ease of implementation means the code should be simple, short, self-contained, effective neighborhood moves and has less parameter. In terms of simplicity SA is better than ACO and GA.

• (g)    Resource Consumption: Resource consumption means the memory space taken by meta heuristics. SA is better in terms of resource consumption when compared to GA and ACO as no intermediate results will be stored.

  

  (a) R101

  (b) R201

  
  
  

  (c) C101

  (d) C201

  
  
  

  (e) RC101

  (f) RC201

  Fig. 6. Solution quality for instance

  
  

Table 7 summarizes the findings of our analysis about SA, GA and ACO. In this table H stands for high, M stands for medium and L stands for low presence of particular attribute. From the table it can be concluded that SA is simple to code but its presence is low on all other attributes discussed above. On the other hand both GA and ACO even complex to code but produces high quality results.

Table 7. Comparative analysis of meta heuristics

	Dataset		Improvement	Time Complexity	Solution Quality	Robustness	Simplicity	Resource Consumpiicti
	Гуре 1	[ype2
SA	MH	L	M	L	L	L	H	L
GA	H	H	MH	H	H	H	M	M
ACO	H	MH	H	M	MH	H	M	H

V. Conclusion and Future Work

VRPTW is an important problem in transportation and it is a well-known NP hard combinatorial problem. Various metaheuristics are used for solving it. In this paper three widely used meta heuristics namely SA, GA and ACO are implemented and an empirical analysis of obtained optimal solution is compared on different parameters. The carried out analysis allows us to draw following conclusion: (1) Resources are expensive and optimization is necessary and meta heuristics are the good choice. (2) There is tradeoff between solution quality and time complexity. (3) SA gives good solution in faster run time. (4) Solution quality provided by ACO and GA is better than SA but the time complexity of GA is high and ACO lies between SA and GA. (5) In terms of robustness both ACO and GA scores high than SA but with high simplicity score. (6) GA is better choice for powerful systems because it provides good quality results with high time and resource consumption. (7) Results produced by ACO is better than GA and SA both in terms of solution quality and time although the differences are not overwhelming. At the end it can be concluded that the choice of meta heuristic depends upon various factors. The main objective is to make a good tradeoff between time and solution quality. In future these techniques can be hybridized with each other and with other method so that high quality results can be obtained with less time complexity.

Acknowledgment

The authors wish to thank Dr. Chander Mohan from Ambala College of Engineering, ambala, Haryana for his suggestions and corrections.