Reliable Mobile Ad-Hoc Network Routing Using Firefly Algorithm
Автор: D Jinil Persis, T Paul Robert
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 5 vol.8, 2016 года.
Бесплатный доступ
Routing in Mobile Ad-hoc NETwork (MANET) is a contemporary graph problem that is solved using various shortest path search techniques. The routing algorithms employed in modern routers use deterministic algorithms that extract an exact non-dominated set of solutions from the search space. The search efficiency of these algorithms is found to have an exponential time complexity in the worst case. Moreover this problem is a multi-objective optimization problem in nature for MANET and it is required to consider changing topology layout. This study attempts to employ a formulation incorporating objectives viz., delay, hop-distance, load, cost and reliability that has significant impact on network performance. Simulation with different random topologies has been carried out to illustrate the implementation of an exhaustive search algorithm and it is observed that the algorithm could handle small-scale networks limited to 15 nodes. A random search meta-heuristic that adopts the nature of firefly swarm has been proposed for larger networks to yield an approximated non-dominated path set. Firefly Algorithm is found to perform better than the exact algorithm in terms of scalability and computational time.
Routing, Shortest path, Optimization, Meta-heuristics, Firefly Algorithm (FA)
Короткий адрес: https://sciup.org/15010819
IDR: 15010819
Текст научной статьи Reliable Mobile Ad-Hoc Network Routing Using Firefly Algorithm
Published Online May 2016 in MECS
Shortest path routing is a classical network optimization problem which determines a least-weighted path between predetermined source and destination nodes in a given network [1]. Recent advancements such as internetworking, smart objects and pervasive computing in telecommunication made researchers to show interest in this field. Contemporary routing algorithms in routers aid in routing through the least cost path for several high performance Quality-of-Service (QoS) applications like industrial WANs, video streaming, video conferencing, etc. The classical distance vector (AODV, DSDV) and link state routing protocols (OLSR, OSPF, ZHLS) implement the traditional Bellman-Ford and Dijkstra’s algorithms that are not sufficient to meet the QoS demands of today’s modern and sophisticated communication networks [2]. The routing algorithm should also consider all desirable parameters such as hop distance, cost, delay, load and reliability influencing the quality of the route in order to achieve optimality in routing [3], [4]. This type of problem is referred to as multi-objective optimization problem which is NP-Hard [2] and NP-Complete [5]. The computational effort of multi-objective shortest path algorithms like k-shortest path algorithm and Martin’s algorithm is high and not scalable for larger networks [6]. In this study, an exhaustive search algorithm yielding the complete set of Pareto-optimal solutions has been implemented that adopts dominance principle to determine non-dominated solutions from the feasible solution set. Non-traditional swarm intelligence methods like Particle swarm optimization, Ant colony optimization and Bee colony optimization are used to determine the approximated nondominated solution set within the feasible region [7], [8]. Firefly Algorithm, a novel meta-heuristic used for complex optimization problems [9] is proposed in this study for computing the shortest path. The study reveals that this algorithm is scalable and robust with a high convergence rate. Different network configurations are used to compare the performance of the proposed algorithm with that of the exhaustive search algorithm and the results are presented.
The remainder of the paper is organized as follows. In section II, a detailed review of the conventional shortest path algorithms are presented. The evolutionary and swarm intelligent algorithms used to solve this multiobjective optimization of routing in MANET so far have been discussed and the literature gap is identified. Section III gives the multi-objective problem formulation of routing in MANET that considers objectives such as delay, hop-distance, load, cost and reliability. The reliability estimation model for MANET is presented. In Section IV, the classical approach of solving a multiobjective optimization problem through which exact pareto-optimal set of solutions is obtained through exhaustive search technique is presented with an illustrative example. In section V, the bio-inspired algorithm proposed in this study that uses the behavior of fireflies in nature is presented with an illustrative example. Section VI gives the experiments carried out in this study to obtain the performance of the proposed algorithm with various network topologies having different network sizes and the results are presented. Section VII presents the conclusion of the study.
-
II. Related work
Packet forwarding and routing in communication network through the least-cost paths identified by the routing algorithms is a well-known research problem. The network topology contains routers as vertices and wired/wireless connections as edges in a typical weighted graph problem with resource limitations constraining each edge [10]. As most of the traditional routing protocols use the conventional shortest path algorithms, many researchers have compared the performance of these algorithms in terms of computational time and efficiency [5][11]. The Dijkstra’s algorithm and Bellman-Ford algorithm are implemented in Link State Routing protocols and Distance Vector routing protocols respectively [12]. The convergence time complexity of Dijkstra’s algorithm is found to be O(|E| log |V|) [13] and that of Bellman-Ford algorithm is O(|E||V|) [14] when configured with |V| vertices and |E| edges. The computational time complexity increases for larger networks and they do not handle graphs having negative weighted edges and cycles [15]. Other conventional methods like Brute-force algorithm and Martin’s Algorithm are applied to multi-objective shortest path problem and they are found to yield pareto-optimal front, limited to small size and low density networks [5], [6]. The time complexity of Floyd Marshall’s algorithm is also known to be very high to yield polynomial time feasible solutions for complex graph configurations [11].
Routing in networks is usually influenced by several criteria such as bandwidth limitation, load balancing and link factors like delay, jitter and hence it is a complex multi-objective optimization problem [16], [17]. In the case of MANET, the routing performance is affected by reliability since the network is self-organized and selfadministered [18], [19]. Pareto optimization through evolutionary algorithms can be an efficient method to yield the approximated pareto optimal front in single run for these multi-objective problems [20]. The application of evolutionary algorithms like Particle Swarm Optimization, Genetic Algorithm, Tabu search, Artificial Neural Networks and Ant Colony Optimization to determine the shortest path with computationally less effort have been reported in the literature [15], [21]–[23]. Firefly Algorithm, a new meta-heuristic finds application in various optimization problems such as makespan minimization in permutation flow shop scheduling [24], scheduling jobs on computational grids [25], optimal supplier selection [26] and optimal placement and sizing of distributed generation in radial distribution system [27]. Firefly algorithm has been applied for network optimization problems like queuing [28], travelling salesman problem [29], clustering and network partitioning [30]. However the use of firefly algorithm to explore the shortest paths in network is rarely reported in the literature. This study explores the application of Firefly algorithm to solve shortest path routing problem and generate approximated pareto-optimal paths in a communication network.
-
III. Route optimization problem
The shortest path problem of a communication network is a network optimization problem with multiple criteria affecting the routing performance. The network consists of nodes connected by links of various capacities and hence there is a flow constraint that restricts the traffic demand and the current load of the link within the capacity of the corresponding link. The problem is to determine the pareto-optimal or non-dominated set of paths from a source node to a destination node which would minimize the link metrics viz., distance, cost, delay, and load and maximize the reliability of the link.
-
A. Formulation
Let G =( V,E ) be the graph representing the network topology, V be the vertex set containing N nodes and E be the edge set. The problem is to obtain pareto-optimal set of routes, T . Ti ϵ T represents a non-dominated solution containing set of edges ( i,j ) that collectively connects the source node to the destination node and the overall objective function vector of the solution Ti , ( DTi,CTi,DeTi,
LTi, RTi ) of the route T i ϵ T is pareto-optimal.
The problem formulation is as follows:
Minimize Distance, DT =∑( , )∈E d.[jX[j(1)
Minimize Cost, Cp =∑( , )∈ECtjXij(2)
Minimize Delay, DeT =∑( , )∈E d-^tjXtj(3)
Minimize Load, =∑(, )∈E lijxij(4)
Maximize Reliability, RT =∑( , )∈еП]Хц(5)
Subjected to,
1 if i =
∑j∈|V| Xtj -∑j∈|V| Xji ={-1 if i = j^i j^i 0 otℎerwise
∀
Xtj ∈ {0,1} ∀(i,j)∈E(7)
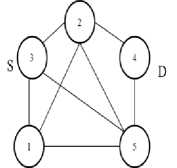
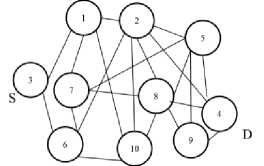
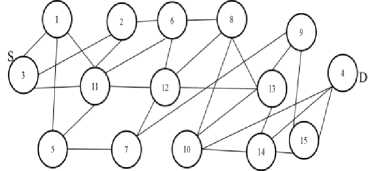
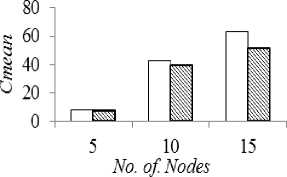
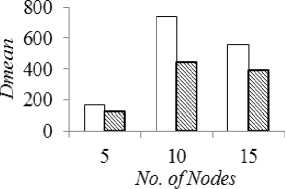
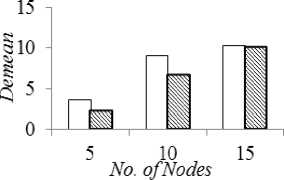
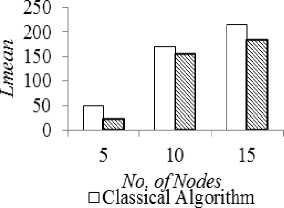
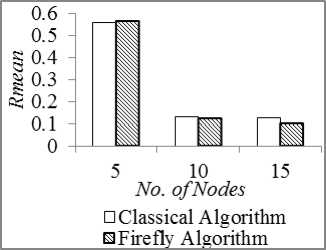
hi + where, dij cij deij I ij rij zij φij Distance of the link (i,j) Cost of the link (i,j) Delay of the link (i,j) Traffic Load on the link (i,j) Reliability of the link (i,j) Capacity of the link (i,j) Demand of the link (i,j) B. Reliability Estimation Because of the unstable network configuration in MANET, it is very crucial to consider reliability in communication that reduces delay and control overhead maximizing the bandwidth utilization [18]. The frequent connectivity loss often creates a major problem in delivering reliable routing. The reliability in connection depends on the durability of the link given by the connectivity period [31]. Through prediction schemes, link lifetime assessment can be made to reduce such failures in network connectivity and maximize the connectivity period [32]. MANET is confronted with dynamic topology changes and hence reliability of the route is a significant component that affects the network performance [31], [33]–[35]. Mobility based reliability prediction model is given in [18], [34] is considered in this study however with few modifications. Consider a node pair (i,j). Their current positions, velocities and directions are given by [(Xi , Vt , Zl),(Xj , У) , Zj)] ,(vt , Vj ) and ( 9i , 9j) respectively where, 0≤9t, 6j ≤2К . The possible position of the nodes after a duration Δ t can be given as, xt (t+Δt)=xt (t)+Δtvt cos 9t(9) Vt (t+Δt)=Vt (t)+Δtvt sin 6t(10) Xj (t+Δt)=Xj (t)+ΔtVj cos 9j(11) Vj (t+Δt)=Vj (t)+ΔtVj sin 9j(12) The reliability of node i is given as, R ={1if lifetime^ > MIN_ _ VALUE(13) 0 Otℎ where, □ 2 _ R$$ij ThTesh-min =(17) ^U - Signal strength based reliability of the link (i,j) Tℎresℎ min- Lower bound for acceptable variation Tℎresℎ min - Upper bound for acceptable variation Overall reliability of the link is given by, Rij = (RU, Ru) (18) IV. Classical approach The multiple criteria considered under study in the shortest path routing problem would yield more than one optimal solution leading to a pareto-optimal or nondominated set. A non-dominated solution in a multiobjective optimization problem satisfies the following dominance principle [36]. “A solution x1 is said to dominate another solution x2 if both the conditions specified below are satisfied: (i) Solution x1 is no worse than x2 in all objectives. (ii) Solution x1 is strictly better than x2 in at least one objective. If any one of the above conditions is violated, solution x1 does not dominate solution x2.” In this study, this dominance theory is used in the classical approach to obtain the entire pareto-optimal set of solutions. Every pair of feasible solutions possible in the given graph problem is tested for dominance to generate the Pareto optimal set of solutions, TND. The classical algorithm presented below is an exhaustive search algorithm that generates all feasible solutions and adopts the dominance theory to extract the nondominated front of a given problem. Therefore, Mobility based Reliability of link (i,j) is calculated as, ( ^-ij (t+Δt) nl _ )------------- lf dU(t+Δt)>transmission range and A^=1 = 0 if Rt=0or Rj=0 (t+Δt)>transmission range Signal strength based stablity model [16] is given below: Relative signal strength of the link (i,j) is given by, RSStj=|SS^d - SS"™| (16) where, RSStj - Relative signal strength ss°/d- Recent signal strength ssiyw - Current signal strength Signal strength based Reliability is given by, //f denotes feasible set ; ND denotes non-dominated set For each node i∈N, find the neighbour list, NHi For each node i in NHS, Tf={S,i} For i=3 to N For each path p in Tf current=last node in p If current≠ D For each node j in NHcurrent If NHcurrent not in p Add p∪ ^^current to Tf Remove p from Tf For each path p in Tf , Calculate (Dp , Cp , Dep, Lip , Rp ) TND=∅ For each path p in Tf For each path q in Tf If q dominates p, p∉^ND TND= TND∪p Fig.1. Exhaustive Search Algorithm with Dominance Principle Example: 1 Consider a network with 6 nodes and 22 edges for illustrating the classical algorithm presented in Fig. 1. Fig.2. Sample Network The exhaustive search algorithm given in Fig. 1 is implemented as follows: i. Initialise feasible solution set f=∅; Nondominated set, ND= ∅; Source S=3; Destination D=4; ii. Initial feasible partial solutions for the given neighbour nodes of S, NH3={1,6}, are f 0= {(3,1),(3,6)}. iii. In every partial solution, the neighbour nodes of the last node are NH1={2,3,5,6}, NH6={1,2,3,5}. The candidate nodes that can enter the feasible set for each partial solution are {2,5,6}, {1,2,5}. So the next feasible partial solutions are f 1= {(3,1,2),(3,1,5),(3,1,6),(3,6,1),(3,6,2),(3,6,5)}. iv. Similarly Step (iii) is repeated for N-1 iterations to obtain feasible complete solutions. f4={(3,1,2,4), (3,1,5,4), (3,6,2,4), (3,6,5,4), (3,1,2,5,4), (3,1,5,2,4), (3,1,6,2,4), (3,1,6,5,4), (3,6,1,2,4), (3,6,1,5,4), (3,6,5,2,4), (3,6,2,5,4), (3,1,2,6,5,4), (3,1,5,6,2,4) , (3,1,6,2,5,4), (3,1,6,5,2,4), (3,6,1,2,5,4) , (3,6,1,5,2,4), (3,6,5,1,2,4), (3,6,2,1,5,4) } v. The application of Dominance conditions yield the non-dominated set from the feasible set by checking every pair (i,j) in f4. For example, consider solution pair (3,1,2,4), (3,1,5,4). When the objective vectors (D,C, De,L,R)( , , , ) =(320,24.8,2.758,145,0.118 4) and (D,C, De,L,R)(3,1,5,4)= (217,20.4,1.629,140,0.383) are compared, it is observed that (3,1,5,4) dominates (3,1,2,4). The test for dominance is carried out for all pairs in the feasible set and the non-dominated set obtained is ND={(3,1,5,4), (3,6,2,4), (3,6,5,4), (3,1,6,5,4)}. The non-dominated set of solutions obtained from classical algorithm is listed in Table 1. Table 1. Non-dominated Set Yielded by Classical Algorithm Nondominated solutions Cost Distance Delay Load Reliability 3-1-5-4 20.4 217 1.629 140 0.38272 3-6-2-4 40.8 211 2.676 133 0.071928 3-6-5-4 40.7 181 2.8 94 0.04836 3-1-6-5-4 84 304 3.48 114 0.092851 V. Firefly Algorithm Firefly algorithm is a recent meta-heuristic developed by Yang that has been used to solve optimization problems [37]. It is an emerging swarm intelligent algorithm that exploits bioluminescence behaviour of fireflies in nature. A firefly in the search space communicates with the neighbouring fireflies/prey through its brightness which influences mate selection and prey attraction. The potential use of this algorithm for determining the shortest path in a network has been explored in this study. The implementation of firefly algorithm for this network optimization problem to determine an optimal path from a source node to a destination node in a given single-source-single-destination weighted graph is presented in the following sections. A. Firefly’s Behaviour Firefly swarm in nature exhibits social behaviour that uses collective intelligence to perform their essential activities like species recognition, foraging, defensive mechanism and mating. A firefly has a special mode of communication with its bioluminescence [9]. The light pattern of the firefly signals the swarm with information about its species, location, attractiveness, etc. The two important properties of the firefly’s flashing light are as follows: i. Brightness of the firefly is proportional to its attractiveness ii. Brightness and attractiveness of pair of fireflies is inversely proportional to the distance between the two. These properties are responsible for visibility of fireflies which pave way to communicate with each other. This communication characteristic of fireflies can be used to solve shortest path search problem in network optimization. B. Scheme of Firefly Algorithm ae(0,1); For each node i∈N, find the neighbour list, NHi For each node i∈N For each node j∈N ^tj = + det] + ^U + ca- Tu For each firefly i∈m, ^ND={S}; current_posi=S; reachedi=0; Fi=0; For each firefly i∈m, Initialize Bl For k=2 to N For each firefly i ∈m If reachedi==0 For each j in ^^current_post∉^ND , Estimate ^current _post,j andВcurrent_post next _P°St =maxj ^current_post,j If next_post == , reacℎedt=1 Fi= Fi+Фcurrent_post. _post ^ND = ∪ {next_P°St }; current_p°st = _p°st =mintFt;Вcurrent_post∗=exp YFbest Fig.3. Firefly Algorithm for Shortest Path Problem A swarm of m fireflies are initially placed in source node S with random initial brightness в0. The selection of next node from a set of candidate neighbour nodes leading to the shortest route is determined based on the attractiveness measure. The transition of the firefly f through a link (i,j) is based on three parameters viz, Brightness, Attractiveness and fitness function. The Brightness of the firefly is estimated by, Bf = (19) where, ^ij - Fitness function estimated by the firefly for the next move у -Absorption coefficient of light Attractiveness estimated by the firefly to determine the desirability of the next position Attj = + Bf +a(rand - 0.5) (20) where, a -Randomization parameter rand - Random number uniformly distributed (0,1) After each transition, the brightness of each firefly is updated based on the fitness of the partial/complete solution of the corresponding firefly. The node with maximum attractiveness is selected by the firefly. This process is repeated till all fireflies in the swarm reach the destination node. By tuning the swarm size and the brightness parameters of the algorithm, more diversified solutions can be obtained from the feasible region. Each firefly in the swarm yields a sub-optimal path leading the firefly from the source node to the destination node. The algorithm is as presented in Fig. 3. Consider the network configuration shown in Example 1 with 6 nodes. The firefly search algorithm given in Fig. 3 is implemented as follows: {0.264,0.296,0.342,0.56,0.404}; = {0.356,0.365,0.378,0.442,0.396}. The node with high attractiveness measure is chosen by each firefly and the partial solution traversed by each firefly is obtained as ND1 {(3,6), (3,6), (3,6), (3,1), (3,1)}. vi. Similarly Step (v) is repeated until all fireflies reach the destination. The approximated nondominated complete solutions after removing duplicates. ND4={(3,1,2,4), (3,1,5,4), (3,6,5,4)} The firefly algorithm is thus applied to solve the network given in Example 1 and the approximated nondominated set of routes yielded along with their performance measures are shown in Table 2. Table 2. Approximated Non-dominated set by Firefly Algorithm Nondominated solutions Cost Distance Delay Load Reliability 3-6-5-4 0.201 0.116 0.240 0.0659 0.00005 3-1-5-4 0.14 0.30 0.19 0.31 0.0021 3-1-2-4 0.05 0.14 0.05 0.08 0.1180 The solutions in the entire non-dominated set shown in Table 2 can be explored by firefly algorithm by tuning the parameters. VI. Experimental Results The firefly algorithm for solving multi-objective shortest path problem is tested for different network configurations for small-scale networks. Simulation experiments are carried out in Matlab, by varying the number of nodes, edges and the link configurations randomly chosen for each objective. For benchmark consideration, non-dominated set of paths are obtained from the classical exhaustive search algorithm presented in this study so as to compare the pareto-optimal set yielded by the firefly algorithm. Fig.4. 5-Node Network Fig.5. 10-Node Network Fig.6. 15-Node Network Several pilot runs are carried out to obtain the optimal swarm size that yields maximum diversity. The firefly algorithm is implemented with a swarm size of 100 fireflies with random initial brightness placed in the source node. Fig. 4, 5 and 6 show the three different network topologies for which the shortest path search is executed using classical and firefly algorithms. The performance of the firefly algorithm is compared with the classical approach for the configurations shown in Fig. 4, 5 and 6. For each of these topologies a pareto-optimal set of routes is obtained by applying the algorithm given in Fig. 1 and an approximated pareto-optimal set of routes is obtained by applying Firefly Algorithm given in Fig. 3. Comparison is made between classical and firefly algorithms on the basis of the mean values of the individual objective considered in the study, as well as the computational time taken by the two algorithms. The performance metrics viz., mean values of cost, distance, delay, load and reliability of the non-dominated set of solutions and the approximated non-dominated set of solutions yielded by classical and firefly algorithms respectively are shown in Fig. 7. □ Classical Algorithm ^Firefly Algorithm (a) Mean cost □ Classical Algorithm ^Firefly Algorithm (b) Mean Distance □ Classical Algorithm □ Fire fly Algorithm (c) Mean Delay ^Firefly Algorithm (d) Mean Load (e) Mean Reliability Fig.7. Mean Values of (A) Cost (B) Distance (C) Delay (D) Load And (E) Reliability of the Solution Set Yielded by Classical and Firefly Algorithm Simulation experiments revealed that the approximated non-dominated paths yielded by the firefly algorithm resulted in minimum mean values of cost, distance, delay, load and maximum reliability when compared to the classical algorithm. It is observed from Fig. 7(a) and 7(d), there is an increasing trend in the cost and load characteristics. This is because of the increase in the size of the path set and the average route length of the path set with the increase in the number of nodes. However from the distance and delay characteristics shown in Fig. 7(b) and 7(c), mean delay and distance of the route initially increases up to a level and later decrease due to the increased density of the network as the number of nodes increases. Fig. 7(e) shows that the reliability characteristics show a decreasing trend as the number of nodes increases. With more mobile nodes, there is frequent topology changes thereby the reliability tend to decrease. Fig.8. Network with 20 Nodes, 130 Edges The scalability of the algorithms is tested with a sample network of 20 nodes and 130 edges. The network topology is shown in Fig. 8. The results revealed that the classical algorithm yielding the entire non-dominated set from the search space could solve problems with network size up to 15 nodes. When it is applied to the graph with 20 nodes, the algorithm could not converge within the maximum limit of simulation period. However, it is found from the study that the firefly algorithm is able to yield approximated non-dominated set of solutions within feasible time limits for reasonably large sized networks (i.e., a network with 20 nodes and 130 edges). The convergence rate of firefly algorithm is found to be 78%. The approximated non-dominated front for the 20-node network by applying firefly algorithm is listed in Table 3. The distinct paths obtained by the firefly swarm (100 fireflies) with the objective value for each criterion are presented. Table 3. Approximated Non-Dominated Front Yielded by Firefly Algorithm for 20-Node Network Nondominated solutions Cost Distance Delay Load Reliability 3-15-19-4 27.9 9015 110 3.532942 6.914 958 0.044630 3-15-13 17-8-7-4 36.2 4126 286 8.820577 44.23 057 0.000081 3-15-1416-4 25.3 4108 176 2.801951 152.1 532 0.044630 3-15-1314-12-19-4 47.6 8083 212 8.718035 67.35 147 0.044630 3-15-1317-19-4 58.5 5992 173 7.579616 32.69 559 0.044630 3-15-1317-12-19-4 55.8 5942 192 9.336274 40.31 509 0.044630 3-15-1314-19-4 54.4 056 221 8.413521 32.83 181 0.000034 3-15-1314-16-4 36.5 7015 199 5.285669 167.8 493 0.000008 3-15-1413-5-4 26.9 5753 235 6.908572 36.17 799 0.044630 The possible convergence to the local optima in a multi-objective optimization problem is prevented in firefly algorithm since the individual agent in the swarm searches path based on its own brightness and the brightness of other agents in the swarm as well as a random value that is added to the attractiveness measure given in Equation (20). Thereby firefly algorithm is able to yield diverse paths from the solution space. The computational time taken by the classical and firefly algorithms is presented in Table 4 to study the convergence of these algorithms for various networks considered in the study. Table 4. Convergence Time of Classical and Firefly Algorithms Nodes Edges Classical Algorithm 6 10 0.0098 10 22 0.1883 15 28 0.6154 20 130 co It is observed from the study that the classical approach of searching the shortest path in a network with more than 15 nodes fails to converge in a feasible time limit. However it is found that firefly algorithm is able to handle large network and generate approximated nondominated set with less computational effort. In order to study the scalability of the firefly algorithm for larger networks, different networks are used by generating nodes in a two-dimensional plane of fixed simulation area. The probability of two nodes i, j being connected is given by Waxman Model [38]. The convergence rate of the algorithm is given by, „ , Number convereged Convergence rate = Swarm size The cardinality of the pareto-optimal set of path, convergence rate and convergence time of the firefly algorithm are presented in Table 5. Table 5. Convergence Statistic of Firefly Algorithms Topology Configuration Convergence rate Pareto-optimal front size Convergence time 20 nodes, 189 edges 0.91 9 0.1507 40 nodes, 773 edges 0.84 17 0.4535 60 nodes, 947 edges 0.81 24 0.6577 80 nodes, 1588 edges 0.68 49 1.1876 100 nodes, 2557 edges 0.59 31 1.7541 Simulation results reveal that when the network size is less than 20 nodes, the convergence rate of the algorithm with a swarm size of 100 was 100%. But the convergence rate as observed from Table 5 declines with the increase in the number of nodes. VII. Conclusion Shortest path routing is a significant network optimization problem that determines the optimal path for traffic flow with minimum resource utilization. In general, network routing problem with single objective criterion is addressed. This study presents an implementation scheme for applying firefly algorithm to determine pareto-optimal path set in a communication network and considers multiple optimizing criteria. The routing performance studied through the simulation experiments revealed that firefly algorithm is a potential search technique to determine the shortest path when classical algorithms encounter scalability problem. This study applied evolutionary algorithm to solve this problem with multiple criteria however not exhaustive. Further the study can be explored to analyse the impact of other metrics such as, bandwidth limits, memory capacity, jitter, etc., on the quality of the solutions. Other new evolutionary algorithms can also be applied for this problem to compare the scalability and robustness of the proposed algorithm for multi-objective shortest path routing problem.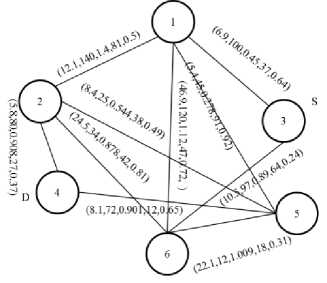
Список литературы Reliable Mobile Ad-Hoc Network Routing Using Firefly Algorithm
- L. Liu, H. Mu, H. Luo, and X. Li, “A simulated annealing for multi-criteria network path problems,” Comput. Oper. Res., vol. 39, no. 12, pp. 3119–3135, Dec. 2012.
- A. W. Mohemmed and N. C. Sahoo, “Efficient Computation of Shortest Paths in Networks Using Particle Swarm Optimization and Noising Metaheuristics,” Discret. Dyn. Nat. Soc., vol. 2007, pp. 1–25, 2007.
- N. Houlden and V. Grout, “Principles of Optimal Interior Routing,” in Fourth Collaborative Research Symposium on Security, E-learning, Internet and Networking (SEIN 2008), 2005, pp. 274–281.
- Y.-K. Lin, “System Reliability with Routing Scheme for a Stochastic Computer Network under Accuracy Rate,” Int. J. Ind. Eng. Theory, Appl. Pract., vol. 20, no. 5–6, 2013.
- G. Janssens and J. Pangilinan, “An empirical evaluation of Martins’ algorithm for the multi-objective shortest path problem,” in The 2011 European Simulation and Modelling Conference, 2011, pp. 252–256.
- X. Gandibleux, F. Beugnies, and S. Randriamasy, “Martins’ algorithm revisited for multi-objective shortest path problems with a MaxMin cost function,” 4or, vol. 4, no. 1, pp. 47–59, Mar. 2006.
- K. Eshghi and H. Javanshir, “A Revised Version of Ant Colony Algorithm for One-Dimensional Cutting Stock Problem,” Int. J. Ind. Eng. Theory, Appl. Pract., vol. 15, no. 4, pp. 341–348, 2008.
- N. Pal and S. Sharma, “Robot Path Planning using Swarm Intelligence: A Survey,” Int. J. Comput. Appl., vol. 83, no. 12, pp. 5–12, 2013.
- S. K. Pal, C. . Rai, and A. P. Singh, “Comparative Study of Firefly Algorithm and Particle Swarm Optimization for Noisy Non-Linear Optimization Problems,” Int. J. Intell. Syst. Appl., vol. 4, no. 10, pp. 50–57, Sep. 2012.
- S. Klampfer and J. Mohorko, “Graph’s theory approach for searching the shortest routing path in RIP protocol: a case study,” PRZEGLĄD ELEKTROTECHNICZNY (Electrical Rev., no. 8, pp. 224–231, 2012.
- K. Magzhan and H. Jani, “A Review And Evaluations Of Shortest Path Algorithms,” Int. J. Sci. Technol. Res., vol. 2, no. 6, pp. 99–104, 2013.
- D. Medhi, Network Routing: Algorithms, Protocols, and Architectures. 2007.
- Z. Tarapata, “Selected Multicriteria Shortest Path Problems: An Analysis of Complexity, Models and Adaptation of Standard Algorithms,” Int. J. Appl. Math. Comput. Sci., vol. 17, no. 2, pp. 269–287, Jan. 2007.
- C. Cooper and A. Frieze, “Average-case complexity of shortest-paths problems in the vertex-potential model,” Random Struct. Algorithms, vol. 16, no. 1, pp. 33–46, 2000.
- B. V. Cherkassky, L. Georgiadis, A. V. Goldberg, R. E. Tarjan, and R. F. Werneck, “Shortest-path feasibility algorithms,” J. Exp. Algorithmics, vol. 14, pp. 1–37, Dec. 2009.
- N. Sarma and S. Nandi, “A Multipath QoS Routing with Route Stability for Mobile Ad Hoc Networks,” IETE Tech. Rev., vol. 27, no. 5, pp. 380–397, 2010.
- W. Alnumay, P. Chatterjee, and U. Ghosh, “Energy Aware Secure Routing for Wireless Ad Hoc Networks,” IETE J. Res., vol. 60, no. 1, pp. 37–41, 2014.
- N. Wang and S. Chang, “A reliable on-demand routing protocol for mobile ad hoc networks with mobility prediction,” Comput. Commun., vol. 29, pp. 123–135, 2005.
- W. Naruephiphat and C. Charnsripinyo, “Routing algorithm for balancing network lifetime and reliable packet delivery in Mobile Ad Hoc Networks,” Ubiquitous, Auton. …, pp. 257–262, 2009.
- J. Pangilinan and G. Janssens, “Evolutionary Algorithms for the Multiobjective Shortest Path Problem.,” Enformatika, vol. 1, no. 5, pp. 322–327, 2007.
- A. W. Mohemmed, N. C. Sahoo, and T. K. Geok, “Solving shortest path problem using particle swarm optimization,” Appl. Soft Comput., vol. 8, no. 4, pp. 1643–1653, Sep. 2008.
- M. Gła̢bowski and B. Musznicki, “Shortest Path Problem Solving Based on Ant Colony Optimization Metaheuristic,” Image Process. Commun., vol. 17, no. 1, pp. 7–18, 2012.
- C. V. Raghavendran, G. N. Satish, and P. S. Varma, “Intelligent Routing Techniques for Mobile Ad hoc Networks using Swarm Intelligence,” Int. J. Intell. Syst. Appl., vol. 5, no. December 2012, pp. 81–89, 2012.
- M. K. Sayadi, R. Ramezanian, and N. Ghaffari-Nasab, “A discrete firefly meta-heuristic with local search for makespan minimization in permutation flow shop scheduling problems,” Int. J. Ind. Eng. Comput., vol. 1, no. 1, pp. 1–10, Jul. 2010.
- A. Yousif, A. H. Abdullah, S. M. Nor, and A. A. Abdelaziz, “Scheduling Jobs on Grid Computing using Firefly Algorithm,” J. Theor. Appl. Inf. Technol., vol. 33, no. 2, pp. 155–164, 2011.
- L. Kota, “Optimization Of The Supplier Selection Problem Using Discrete Firefly Algorithm,” Adv. Logist. Syst., vol. 6, no. 1, pp. 117–126, 2012.
- K. Nadhir, D. Chabane, and B. Tarek, “Firefly algorithm based energy loss minimization approach for optimal sizing & placement of distributed generation,” in Modeling, Simulation and Applied Optimization (ICMSAO), 2013, 2013, pp. 1–5.
- B. Filipowicz, “Firefly algorithm in optimization of queueing systems,” Bull. Polish Acad. Sci., vol. 60, no. 2, pp. 363–368, 2012.
- S. Kumbharana and G. Pandey, “Solving Travelling Salesman Problem using Firefly Algorithm,” Int. J. Res. Sci. Adv. Technol., vol. 2, no. 2, pp. 53–57, 2013.
- J. Senthilnath, S. N. Omkar, and V. Mani, “Clustering using firefly algorithm: Performance study,” Swarm Evol. Comput., vol. 1, no. 3, pp. 164–171, Sep. 2011.
- M. Sivakumar and M. Jayanthi, “Reliability Analysis of Link Stability in Secured Routing Protocols for MANETs,” Eng. J., vol. 18, no. 1, pp. 65–76, 2013.
- H. Zhang and Y. Dong, “Mobility Prediction Model Based Link Stability Metric for Wireless Ad Hoc Networks,” IEEE Wirel. Commun. Netw. …, pp. 3–6, 2006.
- A. Argyriou and V. Madisetti, “Using a new protocol to enhance path reliability and realize load balancing in mobile ad hoc networks,” Ad Hoc Networks, vol. 4, no. 1, pp. 60–74, 2006.
- N. Padmavathy and S. Chaturvedi, “Evaluation of mobile ad hoc network reliability using propagation-based link reliability model,” Reliab. Eng. Syst. Saf., vol. 115, pp. 1–9, 2013.
- M. Eiza, Q. Ni, T. Owens, and G. Min, “Investigation of routing reliability of vehicular ad hoc networks,” EURASIP J. Wirel. Commun. Netw., vol. 2013, no. 1, p. 179, 2013.
- K. Deb, Multi-Objective Optimization using Evolutionary Algorithms. 2001, p. 518.
- S. Yu, S. Yang, and S. Su, “Self-Adaptive Step Firefly Algorithm,” J. Appl. Math., vol. 2013, no. 1, pp. 1–8, 2013.
- B. Waxman, “Routing of multipoint connections,” IEEE J. Sel. Areas Commun., vol. 6, no. 9, pp. 1617–1622, 1988.


