Релятивистская инерциальная навигация и интеллектуальное управление КЛА в римановых метрических пространствах при случайных возмущениях. Ч. 2: кинематика систем отсчета, параллельный перенос тетрад и вращение Вигнера

Одно из обстоятельств закономерного интенсивного развития наукоемких информационных технологий (ИТ) связано с известным фактом появившейся возможности для системной инженерии доступного (для использования в проектировании) применения квантовых и релятивистских макроэффектов, которые лежат в основе управления как космическими летательными аппаратами (КЛА), так и квантовыми системами, находящихся под действием слабых гравитационных полей.

С точки зрения теории управления и системной инженерии, проектирование, например, КЛА, движущегося в искривленном пространстве-времени под действием солнечного ветра или мелких метеоритов как случайных воздействий, или проектирование устройств квантовой памяти (или квантового гироскопа) на основе движения квантовой частицы (со спином ½ или без спина) в слабом гравитационном поле под воздействием случайных возмущений, рассматривается с позиции описания данных устройств как объектов управления (ОУ) в заданной системе отсчета наблюдателя.

В обоих случаях ОУ находятся в пространстве-времени с определенной метрикой и геометрией, в гравитационном поле под воздействием внешних случайных сил и должны быть описаны соответствующими математическими моделями, которые содержат надлежащие физические эффекты. Проявление (не)учтенных в моделях релятивистских и квантовых эффектов отражается на качестве интеллектуального управления, а базы знаний интеллектуальных систем управления проектируются с учетом физической сущности динамического поведения ОУ.

В связи с необходимостью развития методов квантовой релятивистской информатики [1-5] и интеллектуального управления квантовыми и релятивистскими динамическими системами [6-10] возникли методологические проблемы, связанные с отсутствием доступного изложения основ релятивистской и квантовой механик для исследователей в области ИТ [5].

Сами основы релятивистской квантовой механик содержат большое количество «парадоксов», которые в ряде случаев требуют дополнительных знаний из теоретической физики и не булевой логики (квантовой релятивистской нечеткой логики), не Колмогоровской интерпретации вероятности событий (амплитуда вероятностей и отрицательная вероятность) и др., не входящих или вообще не излагаемых в традиционных курсах по физике и механики при подготовке ИТ-специалистов в университетах [11]. Данные факты неоднократно отмечались с разных точек зрения [5, 12-18], а решение данной проблемы существенно зависит от проблемной ориентации образовательных процессов при подготовке соответствующих специалистов и профессиональной ориентации применения приобретенных знаний.

При исследовании релятивистских динамических систем особую роль играют физические аспекты кинематики движения систем отсчета, в которых наблюдателем рассматриваются процессы и приводится физическая интерпретация результатов измерений. Переход из одной инерциальной системы отсчета в другую инерциальную или неинерциальную систему для логического описания результатов наблюдений требует корректного описания системы отсчета наблюдателя и учета ряда новых релятивистских эффектов, не имеющих классических аналогов. Поэтому в данной части работы остановимся на физических и математических особенностях кинематики релятивистских эффектов, а также их учета при исследовании и описании объектов управления в приложении к задачам небесной механики в Солнечной системе.

Кинематика систем отсчета и релятивистские эффекты

При исследовании задач релятивистской инерциальной навигации [8, 19-22], радиолокационных методов управления КЛА и ИСЗ с учетом релятивистских эффектов [8, 23-25] в Солнечной системе [20-33] необходимо учитывать ряд релятивистских эффектов, следующих из особенностей кинематики релятивистских систем отсчета. Из-за отсутствия литературы простого («инженерного») изложения такого сложного вопроса остановимся на изложении некоторых необходимых математических результатов и определений [6-8, 34-36].

В частности, остановимся на понятиях прецессии Томаса и Фоккера, поворотах Вигнера, используемых при исследовании влияния релятивистских эффектов на движение гироскопов. Математические аспекты кинематики и виды релятивистских систем отсчета рассмотрены в Части 1 настоящей работы [37]. Общие вопросы неинерциальных систем отсчета и выбора систем отсчета в процессах измерения, а также их связь со свойствами пространственно-временного континуума исследовались в [37-43] и кратко рассмотрены в Приложении. Здесь обсудим некоторые особенности кинематики систем отсчета в связи с задачами релятивистской инерциальной навигации [20-23, 38-43]. В качестве объекта исследования будем рассматривать важный частный случай общей теории систем отсчета

Электронный журнал «Системный анализ в науке и образовании» Выпуск №3, 2015 год [35-40] – локальные жесткие не вращающиеся системы отсчета с произвольно движущимся началом [41].

Пример 1. Допустим, что заданы три инерциальные системы отсчета S, S', S ". В общем случае в релятивистской кинематике [6, 7] комбинирование двух преобразований Лоренца без вращений приводит преобразование системы S в S" к изменению ориентации декартовых систем осей системы координат в результирующей системе отсчета S ". Если все три системы отсчета S , S, S" имеют произвольную ориентацию, то согласно [41, с. 44]:

x ‘ = D ^-1 x - W"

xW

2 w

2 ^w

2 c

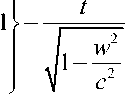
где w - скорость системы отсчета S" относительно S и W" - скорость движения S относительно S "; оператор D отличен в общем случае от единичного.

Физический смысл остальных обозначений в (1) разъяснен ниже1.

Пусть S¹ движется относительно S со скоростью V ; S" движется относительно S¹ со скоростью и¹ . Для величин w и W" имеем в развернутом координатном представлении следующие соотношения [35, 41]

Г     ' 2 А%

1- ^и— г²

V c 7w =-------

(     ' 2 V2

1- ^и—

1 с2

V c 7

W" =--

и ’ V c ²

1 -

V

, и V

^{1 +} -г

Vu ‘ + и'

и 'V c ²

1 - иц;

c ²

1 -

, и 'V

1+

D W " = - W .

Если и ' параллельна V , то из (2) следует

W " = -w = -

V ( 1 + к ).

2;

1     1 и

1 + к — c2

п %

J7

—

, 2 1 и_ c 2

, и

и ' = kV ,  D = 1 .

Для инфинитезимального преобразования S'—»■ S" , при котором скорость и ' является бесконечно малой величиной, уравнение (1) принимает вид:

1 Федоров Ф.И. Группа Лоренца. – М.: Наука, 1979. – C. 180.

1                   1 ID 1 x = x + — < 1

—

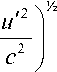
—1Л(VXdV)xx], dV = W — V

В результате получим:

D 1 x = x + (Qx x);

Q =

—

c ²

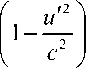
— 1

( V X dV ) .

Из (4) следует, что оператор D представляет собой бесконечно малый поворот тетрады вокруг вектора Q .

Пример 2. Допустим, что имеется точечный компас (материальная частица), определяющий конкретное направление, и задана скорость V ( t ) частицы относительно системы S , dV = Vdt . Системы S’ и S "  в рассматриваемом приближении являются мгновенными системами покоя частицы. Преобразование S¹ ^ S" является инфинитезимальным преобразованием Лоренца без вращения. Если силы, действующие на компас, не сообщают ему момента вращения, то направление компаса в момент t относительно S ‘ совпадает с его направлением в момент ( t + dt ) относительно системы S " . Из (4) следует, что вектор Q при dV = Vdt определяет поворот осей системы S в момент ( t + dt ) для приведения их к одинаковой ориентации с осями системы S ". По условию направление компаса неизменно в системе отсчета покоя частицы. Следовательно, в системе S направление компаса изменяется угол, соответствующий вектору Q [41, C. 45].

Таким образом, компас прецессирует в системе S со скоростью

to =

^

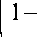
S2)

— 14 V X V ).

dV

Здесь V = —— - ускорение точечного компаса. В первом приближении при i 9 <<  c имеем:

to = —

V x V

2 c ²

Эффект (6) называется прецессией Томаса. Математические аспекты анализа и поправок к формулам (5) и (6) можно найти в [43 - 45].

Отметим теперь некоторые особенности рассматриваемых преобразований систем отсчета.

В символической записи два последовательных преобразования Лоренца S ^ S¹ и S ' ^ S" имеет вид x ' = L_ikx^k , x ' = L ‘ x ‘ ^k и дают результирующее преобразование:

x ” = ( L'L ) x^k ,                                            (7)

т.е. (7) также является преобразованием Лоренца.

В случае инфинитезимального преобразования Лоренца без вращения для S ‘ ^ S" имеем

^Li k = ^ ik ^{+ Э} г к ;   ^Э ^ к = 0, ^Э ^ 0 =   ^Э 0 ц = ^iV p / c, ^Э 00 = ⁰

где V^ — 4-скорость движения системы S” относительно S ‘ , э ‘_к - тетрада.

ТогдаL‘' = (^к + э' )Llk = Lik + э' Llk. Если x. = f. (т) - мировая линия произвольного движения частицы в S , а т - собственное время частицы, то 4 - скорость системы S' относительно S имеет вид

U ( т ) = dx ^л ' dт

= f ( т ) . Коэффициенты

Lik

можно рассматривать как функции L_ik ( т ) . Тогда

L ”_к = L (т + d т ) , а для функции L_ik ( т ) можно получить [41, с.94] следующие уравнения:

-/■ = L,^ ¹ , S t = ( JU - U , U_; ) / c\                        (8)

т.е. (8) совпадает с переносом Ферми-Уолкера (см. Часть 1). Сами коэффициенты L_ik и ^_к удовлетворяют соотношениям релятивистской кинематики [6, 7, 41]:

L A = 5 . L , , U = 0; L.^L ^ - 0,

L _v i r u_s =- LU, ; L ^" L m S " =- ( LU' )( L . , U - ) / c ².

Физически уравнения (8) определяют переход от фиксированной (лабораторной) системы отсчета S к мгновенной системе покоя S ' и системе координат { x ' } .

Пример 3. Допустим теперь, что к рассматриваемой в примере 2 частице присоединен единичный вектор э ' ( т ) . Компоненты этого, вектора предполагаются не изменяющимися во времени относительно пространственных осей S ' ( т ) . Смещение вектора э ' ( т ) происходит, таким образом, без изменения его ориентации (см. пример 2), а в системе S его компоненты имеют вид:

э,(т)=эк(т) L т><(т)^(т)

Согласно (8) и (9), имеем:

d э, (т) =э' (т) dL, (т) =э' (т)^иЦ,-UU,  (э 1U)U, -U,(э 1 U).

dт      k       dт      k            cгc

В силу ортогональности э_; U¹ = 0 , из (10) следует

£ эД т ) ₌ ( !L Ul) и

J dт и является частным случаем (4). Следовательно, имеем перенос Ферми (см. Часть 1).

Из (11) следует, что при т = 0 (если S '( т ) совпадает с S ) имеем э. = э к . В этот момент скорость частицы равна нулю. Таким образом, компоненты единичного вектора различны в системах отсчета S и S ' ; этот вектор совершает, согласно примеру 2, прецессию Томаса относительно S .

Пример 4: Жесткая система отсчета . Будем называть в дальнейшем систему отсчета жесткой, если расстояние между двумя точками системы, измеренное покоящейся относительно нее измерительной линейкой, не меняется со временем [41, с.94; 43]. Допустим, что в инерциальной системе отсчета заданы псевдодекартовы координаты Лоренца X¹ , ,’ = 0,1,2,3 , через которые криволинейные координаты x выражаются в виде:

x = xi (Xk)

Дифференцируя (12), имеем

i dx — —- dXk — Ai dXk.

dxkk

Аналогично имеем dXi—^X-dx1 = Adxk.

dxkk

Таким образом, имеем i-Aifdx1*               2     dVdxk*              Л1 4m ^ЛАЛ- dx — Al Akdx ; Ai Ak — °k ; ds — gikdx dx ; gik — gki — ilmAi Ak — Ai Ak Ai Ak .

Согласно (8), переход от фиксированной системы S^k к мгновенной системе S ‘ ( т ) с системой координат х^г имеет вид x_t — x ‘ L_ki ( т ) . Для того, чтобы частица находилась в начале координат покоя S ‘ ( т ) , необходимо непрерывное смещение начала координат в S ‘ ( т ) , т.е.

xi— fi (Т)+xkLAA.

Рассмотрим преобразование X i ^ x i в виде

Xi— f, (t) + xv Lvi( t),(16)

где коэффициенты L_vt ( t ) являются решением уравнения (8).

Движение частицы в плоском пространстве-времени X определяется уравнением мировой линии С в параметрическом представлении

Xi—fi(0; dX7\—f(t)—yi(T; A— DUr d (т)

Согласно (16), преобразование к новым координатам x i — ( x , y , z , ct ) в вещественном представлении имеет вид

X i — f i ( т ) + A k ( t ) x^k . (18)

Здесь, как и в (14), (14а), A i ( т ) - коэффициенты преобразования Лоренца от системы ( X i ) к мгновенной инерциальной системе покоя частицы. Такое преобразование, как было показано выше, есть результат применения последовательных инфинитезимальных преобразований Лоренца без вращений. Поэтому коэффициенты A i ( т ) удовлетворяют уравнениям (8), которые в вещественном представлении имеют вид [41, c. 234]:

dA k ( г ) — A k ( т )(й _к и - UU i ) c -² — W i А¹( Т ) , W ^ik — c-² ( ua¹ - AU ) — c-² U i, A ^k ]   (19)

В (19), W ^ik – компоненты соответствующего тензора в Лоренцевой системе координат.

Следуя [41, c. 217, формула (9.30)], коэффициенты А¹_к (т ) определяются в ортогональной системе через компоненты тетрады э¹^_к) ( т ) = А¹_к ( т ) . В результате имеем следующие уравнения для перемещения тетрады вдоль мировой линии С :

d э X а ( т )       .   .    / _х

"’ ⁽ ) = W э\ к , ( т ) .                                        (20)

а т

Таким образом, уравнение (20) совпадает с уравнением для случая плоского пространства с Ло-ренцевой системой координат. Следовательно, вдоль мировой линии С тетрады ∋ ⁱ претерпевают перенос Ферми – Уолкера.

Пример 5. Рассмотрим теперь случай, когда частица покоится в системе R с S в начале координат x ^ = 0 . В системе S координаты x^l определяются по (16), а временная координата t совпадает с собственным временем т частицы. Система отсчета R является 3-мерной, в которой точка p е R с тремя постоянными значениями пространственных координат x ^д , а координаты x^l = ( x ^ , ct ) с изменяющимися t описывают последовательные события в p е R .

Дифференцирование (16) с учетом (8) приводит к виду dx. =(u. + xvLv^ ) dt + Lvi ax.                            (21)

Так как выражение для интервала ds2 определяется в виде ds2 = dXldXl, то из (14а) получим ds2 = dx2 + dy2 + dz2 - c2dt2 (1 + gvxv c 2) , xl =(x^, ct ) = (x, y, z, ct),            (22)

где gv = gv (t) = Lvl и = Lv fl. В системе отсчета S метрика определяется по (22) и в малой окрестности (в пренебрежении величинами второго порядка малости относительно x^) принимает вид gk = Пк - 5ioSk02g^ (t) Xхc(23)

Функции g_x ( t ) равны пространственным компонентам 4-ускорения A ( т ) частицы в системе S , которые по определению равны

4 ( г ) = 4 t ( т ) А к = э к„ А к .                                  (24)

Если заменить т ^ t в А_к ( т ) , то получим g _x ( t ) = А _х ( t ) . В искривленном пространстве-времени в произвольной системе отсчета S с координатами x уравнения типа (17) по-прежнему определяют мировую линию С , но в отличии от СТО, теперь 4-ускорение равно абсолютной производной от скорости U . ²

• ² Здесь еще раз отметим, что если данный вектор переносить параллельно из одной точки p в другую точку p вдоль некоторой кривой, соединяющей эти точки, то результирующий вектор в случае искривленного пространства зависит от формы кривой и не зависит от формы кривой, если пространство плоское. Это одно из 7

На мировой линии С как и в случае плоского пространства-времени определяет поле тетрад, которые подвергаются переносу Ферми - Уолкера. Если вектор э^Д0) в точке О параллелен 4-скорости, то это будет выполняться и на всей кривой С . Для данного тетрадного поля во всех точках на С выполняются следующие соотношения:

э\ х = —;  э\ . U = 0;  W'k э, = с с~2Ul(Ak э( . );   э'  A = 0.

• (0)     с ’      (а)    1       ’             (а)к              \ к   (а)кГ       (0)    lv 7

Если поле тетрад выбрать в виде (25), то формула переноса для ∋ ⁱ определяется в виде

D эl Jr)                  zх

--^ A— = w« э   = c"U ( A l э_м Д                   (26) d r                   ^{( v} ) ^{1            (        ( v ) 1} )

Величины Ui и Ai можно считать для данной мировой линии известными функции от r и однозначно определять векторы тетрады э^(г) из уравнения (26) при заданных начальных условиях э^^ ( 0 ). Следовательно, можно считать известными величины gv (Г)=эlv)(r) Al (r) .

Пример 6. Допустим, что задано преобразование x = f (t)+ э (zJt) x - —Г (2^)( t ) x x ^.(28)

где э^ ( r ) является решением (26); Г^l^ ( r ) задается формулой [41, c. 235]:

г; l. )(г)=э(; ) э-„)Г'„ ( p ) I _1 )(r)

Символы Кристоффеля Г ¹ _Ы ( p ) считаются известными функциями от r в точке p на мировой линии С с координатами x^l = f^l ( r ) . Преобразованию (28) удовлетворяет система координат S : x i = ( x ^ , ct ) со следующими свойствами [34-36]: 1) кривая С определяется уравнениями

X ^м = 0, t = r (частица находится все время в 0 системы отсчета R, 0 с R ; временная координата t равна собственному времени частицы); 2) локально при любом t метрика имеет форму (23).

Уравнения (26) можно записать, используя соотношения (25), (27) и (29), в виде [41]:

d э i х ( r )                            i

• — ■ /   =-г l, ( р ) и- a- ; , , + -^ u s g , =- с г ( „ _г ) + c-Uig, .                 (30)

Компоненты 4-скорости и 4-ускорения частицы в системе S имеют вид существенных различий между плоским и искривленным пространствами с точки зрения теории относительности (см. Приложение 1).

i

Ui

= LU = c ^ ^ k op cS_m ; A , = L , A , = э ( , ) A i = ( g , ,0 ) ; L , ( p ) = э ( , , , L , ( p ) —( p ^ (31)

Во всех точках кривой С система S является локально псевдоевклидовой [41, с.236], локально метрика в S имеет ту же форму (23), что и в случае плоского пространства-времени. Таким образом, система отсчета R является корректным релятивистским обобщением ньютоновской не вращающейся системы отсчета [20, 38-41].

Пример 7. Допустим, что в начале 0 системы R расположен точный компас, который показывает все время одно и то же направление относительно координатных осей в R (физически таким устройством является гироскоп, который в S не подвергается действию крутящего момента), т.е. описывается пространственно-подобным вектором с постоянными компонентами [20, 38, 40]

э ¹ = ( э ^ц ,0 ) ;   э ^ э^ = э ^ц э ^ц = 1.                                 (32)

Из (30), (31) и (32) следует

'   = — c ^r ( о- ) ^k " " / ^ g - ^k ' ) = "  С ^Г i O ' ) ^k i" ^k ' ⁺ c² UA =f d f-1  ■ d f-1 .     ⁽³³⁾

ат                c                                     ^ ат 7ф v dT Jt

Из (33) следует, что единичный вектор ∋ ⁱ , описывающий направление гироскопа, прецессирует

в системе отсчета S . В (33) 4-вектор

(d^- 1

I d ^T J t

= c"^UⁱA_l э '

является формой релятивистской прецес-

сии Томаса (11); соотношение

d ∋ ⁱ

d T

= c "²P V . з ( ^г ) э ' =- с Г‘ , э ^v

( 0 v )     '                  ( 0 v )

описывают эффект, присутству-

ющий даже в случае свободного падения частицы и называется прецессией Фоккера.

Пример 8. Рассмотрим теперь одну из разновидностей обобщения результатов из рассмотренных выше примеров 1 и 2 (см. рис. 1).

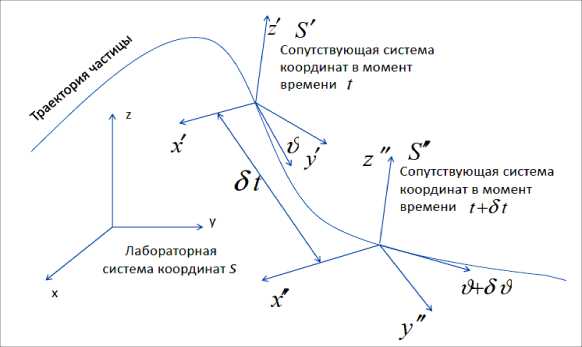
Рис. 1. Пример двух Лоренцевых жестких реперов движущейся частицы с точки зрения лабораторной системы отсчета

В Части 1 настоящей работы отмечалось, что результирующее релятивистское 3-вращение репера, сопутствующего частице М , следует рассматривать как сложное, состоящее из двух вращений: внешнего, определяемого вращением элемента среды, и внутреннего – добавочного (принудительного). Один из таких вариантов обсужден в Примере 7. Необходимые обозначения приведены на рис. 1.

Здесь обсудим вариант (приведенный на рис. 1), в котором исследуется кинематика релятивистских эффектов мгновенных переносимых систем отсчета S ' ^ S" с точки зрения лабораторной системы S ^ S ' ^ S" .

С точки зрения наблюдателя в системе S события в системе S’ определяются как

cAt ' = у (cAt - PA r); Ar ' —Г(A r - Pc At)

В (34) обозначено P c - скорость S' в системе S , а коэффициент Г - специальный нормирующий множитель (диадик), связывающий интервалы A r, A r ' событий в S и S’ . Аналогично, события в S с точки зрения S’ имеют вид:

c A t — у ( c A t'a aA r ' ) ; A r — Г ⁺ ( A r'a a c A t ' ) ,                        (35)

где c a - скорость лабораторной системы S с точки зрения S ' . Для введенных коэффициентов выполняются следующие соотношения [46]:

Гр + Ya — 0; Ya + yP — 0; Г+Г —(I - PP) X — I + у2PP; ГГ+—(I - aa )-1 = I + y2aa, где I - 3-мерный единичный диадик. Как и ранее у2 — 1/ (1 -P ) — 1/ (1 - a2 ). Тогда соотношение Лоренца типа (1) – (4) имеют вид

dr'_ Г( V - cP)     ,_dV '_Г[(1 - PV / c) I + (V - cP) P / c ] a

V — --- — --Z----------Г ; a — ---- — --------------------------T----------- .

dt'    y ( 1 - P V / c )         dt '              Y ² ( 1 - P V / c ) 3

Для последовательности S ^ S ' ^ S" имеем следующие взаимосвязи коэффициентов:

f — yy'(1 - Pa); y'P" = y'( yP + PT); fa" — у (fa'+Va); Г — ГГ-Yf'a'P .

В [46] предложено в композиционном правиле перехода S ^ S ' ^ S " представить коэффициент Г в виде произведения двух факторов: диадик вращения R и диадик чистого смещения Г₆ как

Y 1

буста (жесткого 3-репера). Таким образом, имеем Г — R -Г • При этом Ге — I +--P • P. Для в                       y +1

мгновенной системы отсчета S' коэффициент Г' определяет вращение относительно системы координат S ' (при инфинитезимальном смещении S ' ) на угол 51^' (относительно не вращающихся осей координат, обозначаемых в S ' через вектор т' ). Тогда Г' — I - 5^ ‘ m ' х I . Если обозначить через to ' мгновенную угловую скорость в S ' при ее инфинитезимальном смещении из S' ^ S'' , то имеем to — ( d ^ ‘ / dt' ) т' , а исходное уравнение для коэффициента Г будет иметь вид [46, с. 530, формула (20)]:

dГ _ Y2 (Г-a)P toхГ dt       c         y

Тогда из соотношения Г — R -Ге следует, что уравнение рассматривается как система dR=r dt

Y2 (Г. • a) в  d Г в

—-- — ——

c

dt

Г в

1 to х R

—

Y

,

d Г в = dt c

Y'

Y 2 ( y + 2)/ а

(  ,  )(Р• a)РР .

Первое уравнение в системе (37) при to = to,

c

YY

----- ( а х в ) преобразуется к виду

dR dt

- R х ^

to х R

Y

Из (38) следует (как частный случай) отмеченный в Части 1 данной работы эффект разделения вращения репера (как сложного процесса) на две составляющие: компонента вращения системы отсчета как специального диадика R определяется двумя угловыми скоростями to и to' . Первая из них to (скорость прецессии Томаса) определяется линейной скоростью и ускорением движения частицы. Вторая угловая скорость to' определяет внутреннюю структуру (внутреннюю степень свободы) принудительного поворота мгновенной системы отсчета S' .

Таким образом, угловая скорость прецессии Томаса to определяется в мгновенной системе отсчета при ее инфинитезимальном смещении по траектории движения частицы. В частном случае, при 5у' = 0, имеем to' = 0 и получаем жесткую тетраду Ферми - Уолкера dR+

---= to х R , dt T что приводит к параллельному переносу Ферми – Уолкера. Если потребовать в начальный момент t = t0 выполнение условия сохранения значения R = R (t0 ) вдоль всей траектории движения частицы, то из (38) следует to' = —yR(t0 ) • to или после несложных преобразований [46] получим

to = -—^—- (а' х а). c ( Y + 1)V      7

Из (40) следует количественная оценка угловой скорости принудительного поворота системы S ' при инфинитезимальном смещении S ' ^ S "  за счет переноса Ферми - Уолкера с точки зрения наблюдателя в системе отсчета S .

Сопутствующие и собственные системы отсчета

Математическое решение задачи об инерциальной навигации состоит в определении относительно известного наблюдателя закона движения (преобразования координат) для рассматриваемой точки по заданной системе ее ускорений вдоль искомой мировой линии [20].

Таким образом, задачей навигации, в общем случае, является определение координат положения объекта управления (например, КЛА в пространственно-временном континууме) относительно фиксированной (лабораторной) системы отсчета (например, относительно Земли). Для определения координат объекта управления наблюдатель (находящийся на этом объекте) использует как наблюдения за положением светил на небесной сфере (Солнца, Луны или звезд), так и показания приборов, находящихся на самом объекте (например, акселерометров, с помощью которых можно определить ускорение объекта в каждый данный момент) [39]. С помощью указанных процедур реализуется алгоритм решения задачи навигации. В случае, когда для определения положения объекта управления в пространстве – времени используются исключительно показания приборов, находящихся на объекте и начальные сведения о его положении в момент старта, имеют дело с задачей инерциальной навигации. Здесь в качестве приборов измерения используются исключительно часы и акселерометры, определяющие вектор ускорения в каждый данный момент времени. При этом рассматриваемый объект движется по мировой линии без вращения (последнее условие может быть достигнуто за счет использования системы гироскопов, расположенных на объекте).

Математический анализ задачи релятивистской инерциальной навигации проводился во многих работах [20-23, 47, 48] и требует дополнительных уточнений в определении систем отсчета [32-42]. Здесь дадим необходимые дополнительные определения, используя результаты Части 1 и предыдущего раздела настоящей работы.

Выделенные сопутствующие системы отсчета

Среди выделенных систем координат и систем отсчета особое место занимают сопутствующие локальные и глобальные системы координат, представляющие собой системы координат Лагранжа [20, 32]. Если заданы две координатные системы, связанные между собой функциональными зависи- мостями za = фа (хв ) и z4 = f (хв, х0 ) а, в = 1,2,3, то координаты ха и za называются лагран- жевыми координатами соответствующей системы отсчета. Системы координат xi и zi называются сопутствующими системами координат для системы отсчета с лагранжевыми координатами ха и za . Систему отсчета с координатами xi называют системой наблюдателя (или эйлеровой системой), а систему отсчета с координатами е = е1 (х1) - сопутствующей (или лагранжевой) системой.

Пример 1. Линейное преобразование дифференциалов координат от х1 к е имеет вид d^ = dkde,k; de = bkjdxJ (a'bk = 6)

Матрица || a ' || в точке М может быть произвольной с определителем А = | a ' | * 0 и — = | b '| * 0 .

Для общих нелинейных прямого и обратного преобразований х¹ = х¹ ( е^с ) и е = е ( х¹ ) в точке М

.   ах1 кк  де имеем a, = —г  , b =--- k   де д, , j   дх}

M

M

Если данные равенства справедливы во всех точках пространства,

то дифференциальные преобразования dd и de называются голономными. В общем случае данные равенства выполняются только во взятой точке М и соответствующие преобразования являются локальными и называются неголономными.

Наличие метрики пространства-времени позволяет сконструировать соответствующие выделенные системы с помощью неголономных канонических систем координат в каждой точке пространства V и с помощью тензоров, определяющих метрику. Система мировых линий, индивидуализированных условиями е = const , совпадает с системой мировых линий n^a = const , если переменные е и n k связаны преобразованиями n^a = f ^а ( е^в ) , П 0 = f ( е ' ) . Все системы координат Лагранжа, соответствующие данным фиксированным мировым линиям и связанные между собой указанными преобразованиями, образуют систему отсчета Лагранжа.

Общий вид для метрики сопутствующей системы отсчета ds2 = g,d?d? = g 00 (d? )2 + 2 g„ 0 d?d? + g„el^d^             (41)

в рамках одной и той же системы отсчета с ненулевыми мировыми семейства линий С можно привести к виду [20, c. 57]

^{ds 2} = ( d n ⁰ ) ² + ² g a 0 ^d n „ ^d n ^{0 + g}_al3^d n ^{a d} n ^P ,                          ⁽⁴²⁾

если принять n ° = J^ g 7( ? n d ? = ф ( ? - ? ) , n " = ? „ • В (42) обозначено

₌g 0 ^g a 0 ГТ

—

бф а _ „    бф бф

б?"; ge = ge + ??

- 2 g „ о

бф 1

б?

Таким образом, во множестве систем координат Лагранжа, соответствующих одной системе отсчета, существует система координат n" , в которой g00 = 1. Для мировой линии выделенного семейства мировых линий С (при ? = const) может быть введен глобально переменный временной параметр т + f ?" ), для которого во всех точках линий С имеет место равенство It = ds / c . Тогда метрика (42) примет вид ds2 = c2 It 2 + 2 cga ^„Тт + gapd"?.

Метрика типа (43) используется для описания системы отсчета наблюдателя в задаче релятивистской инерциальной навигации.

Пример 2. В каждой точке пространства значение глобальных временных переменных различны. Выражение для метрики (43) можно записать в виде (см. Часть 1)

ds2 = c2 dt2 + hyd- d- - he = g в - s - о g ,о; dt = It+1 g „о d?.(44)

Из (44) следует cd ( t - т ) = g_ad ? " = d Q * 0 .

Если dQ является дифференциалом функции Q(?",t) , то справедливы соотношения 6Q dQ gaa0 = тт„- — = 0- Q = Q? ).

б? бт

Отсюда следует выполнение условия интегрируемости уравнений (44) в виде б1„^ J^gdo = 0; Sggo = о

б?5  б?      бт

Из (45) следует, что ga „_о не зависит от т , а значения t и т связаны равенством t = т + ф ( ?“ ) . Системы координат с метрикой (44) называются синхронными.

Пример 3. Отметим некоторые полезные для дальнейших исследований свойства преобразований Лоренца. Согласно преобразованию Лоренца Lⁱ для двух различных инерциальных систем отсчета { y i } и { x^k } имеем y i = L_kx^k . Если трехмерные повороты и скорость V движения системы { y i } относительно { x^k } малы, то компоненты матрицы L_k могут быть представлены в виде

L'.. = 8. + у, L" = ——; L" =-9; L = 1.

cc где У и — - бесконечно малы. Шесть компонент (независимых) антисимметричного тензора у c рассматриваются как независимые параметры, определяющие бесконечно малое вращение в 4-мерном пространстве Минковского. Согласно Части 1, преобразование Лоренца с компонентами (46) можно записать в виде [20]

(в

Li = 8i + yi ,   y0 =; Ю a =a cc

Матрица y ^j в декартовой системе координат может быть записана в виде

0     у3    го2   —9 / c II У   0   —У  —9/c У«-||= 2 —го2   У     0   —9 / c .                                     (48) 9 / c 9 / c 9 / c    0 бесконечно малый 3-мерный простран-

В (48) аксиальный вектор to = ( to\ to² , У ³) описывает ственный поворот осей декартовой системы координат у “

относительно системы x“ , а полярный

вектор V = ( 9ⁱ,9²,9ⁱ ) - бесконечно малую 3-мерную поступательную скорость инерциальной системы ^y относительно системы x , координаты которых связаны данным бесконечно малым преобразованием Лоренца.

Отметим, что в системе координат наблюдателя с базисными векторами ∋ компоненты матрицы ||y^j || бесконечно малого преобразования Лоренца (48) имеют вид У = du^j — a^ju^l , где u^l и a^j -компоненты скорости и ускорения движущейся частицы соответственно.

Пример 4. Рассмотрим теперь полезное обобщение формулы Кориолиса из ньютоновой механики на релятивистский случай с учетом более общих свойств переносного движения. Такое обобщение необходимо при анализе физического смысла показаний акселерометра в задаче инерциальной навигации. Рассмотрим три системы отсчета в локальном 3-мерном объеме на мировой линии С в близких точках M и M' на С , отвечающих моментам времени т и т + d т при d т ^ 0. Координатными базисами для введенных систем отсчета являются: 1) локальная (основная) система наблюдателя; 2) переносная подвижная система (вращающаяся и деформирующая); 3) система относительного движения.

Первая система отсчета характеризуется компонентами координат x^а и базисами э_а = const , скоростью V_abs = д r / дт , где т - собственное время на мировой линии С . Вторая система отсчета определяется координатами у“ и базисами э_д , переменными относительно э_д, со скоростью V_tr = д r / дт в системе { x“ } (вектор скорости имеет компоненты 9 в базисах э_а и 9 в базисах э“ ). Третья система со скоростью V“_rd =д r / дт = 9“ э_а имеет компоненты, которые можно рассматривать как в тетраде э_д с компонентами 9^а в э_д, так и в тетраде э_а с компонентами V^a_ге1 .

С точки зрения наблюдателя с базисом ∋ (считая его инерциальным) имеем [49]

a abs    a tr ⁺ a rel ^{+ 2} ^ rel ⁽ e ap ^{+ Ю} сф ) ^{Э .}

В ⁽⁴⁹⁾ обозначено   e e = ¹ ( V „ ^ +V e ^ a )

–

компоненты скоростей деформации;

to_ap = 2 (^“ ^ — V ^“ ) — компоненты тензора вращения в переносном движении в 3-объеме. Следует подчеркнуть, что выражение (49) справедливо в СТО и ОТО в любых криволинейных координатах; сохраняет свой вид и в случае, когда рассматриваются все ускорения относительно неинерциального наблюдателя с базисом ∋ [20, 49].

Ускорения для dr и dr определены по отношению к одной и той же системе отсчета (инерциальной системе), а ускорение для dr определяется относительно системы наблюдателя, «вмороженной» в переносную систему отсчета. Абсолютное движение и переносное движение точек можно определять, таким образом, относительно локальных инерциальных тетрад, а относительные ускорения – по отношению к «вмороженным» (сопутствующим) тетрадам наблюдателя, движущегося вместе с «вмороженными» тетрадами систем отсчета (с учетом ускорений деформаций e и вращения to_ap тетрад в переносном движении).

В ньютоновой механике подразумевается, что «вмороженная» переносная система отсчета связана с твердым телом (в этом случае и устанавливается формула Кориолиса). Формула (49) является обобщением аналогичной формулы Кориолиса для деформируемых систем отсчета в переносном движении для СТО и ОТО.

Дополнительные вопросы анализа неинерциальных систем и их влияние на процессы измерений можно найти в [6, 7] (см. также Приложение и Часть 3). Здесь остановимся кратко на понятиях сопутствующей и собственной системы отсчета.

Пример 5. Векторы э₀ = и , заданные в каждой пространства, определяют собой векторное поле. Огибающие векторные линии этого поля можно рассматривать как мировые линии соответствующей сопутствующей системы отсчета. Так, если в пространстве Минковского все векторы ∋ параллельны, то их огибающие - прямые линии. При э₀ = и получаются системы отсчета, определенные геометрическими свойствами самого пространства в ОТО. В результате в ОТО соответствующие системы сопутствующих линий представляют собой геометрически выделенные характерные сопутствующие системы отсчета [20, с. 46].

В ОТО в качестве сопутствующей системы отсчета рассматривается не инерциально движущийся континуум [40] (называемую, часто «физической лабораторией движущегося наблюдателя»). В этой сопутствующей системе отсчета, согласно Части 1, соблюдается и сохраняется всегда условие равенства нулю 3-скорости u ⁰ / u ⁰ . Определение такой системы отсчета в частном случае совпадает с системой отсчета Ферми – Уолкера.

В этом случае определяется сопутствующее пространство, т.е. правила выделения частиц среды, синхронизованной с данной. При таком определении сопутствующей системы отсчета возникает возможность использования локальных или обобщенных преобразований Лоренца, т.е. принципа локальной справедливости СТО в ОТО, что создает возможность последовательно учесть эффекты СТО в ОТО. Рассмотрим одно из возможных определений сопутствующей системы отсчета [50].

В фиксированном пространстве-времени вводятся 4-реперы {э.}, {эi} , которые связаны с мет-ik i k рическим тензором соотношениями g^ =ээк, g =э э . Эти соотношения позволяют для произвольного 4-вектора А задать координаты: контрвариантные Ai и ковариантные A по формулам

A = A i э. = A э¹ . С каждой движущейся частицей континуума связаны подвижные 4-реперы { э.₀} , { э i } , в которых вектор A имеет координаты A i , A_o . Подвижный 4-репер можно разложить по базису неподвижного, получив его координаты: э. ₀= ( э. ₀) k э_к = ( э. ₀) э ^к .

Таким образом, для определения сопутствующего пространства-времени необходимо ввести уже движущиеся ортонормированные 4-реперы { э.₀} , {э_o i } с соответствующими координатами x_{t 0}, x^ , относительно которых метрический тензор имел бы псевдоэвклидову форму П = П = diag { - 1, - 1, - 1, + 1 } . При этом выполняются соотношения ортонормированности: ( э._о • э_{к 0}) = п = ( э i ₀ • э ^k ₀) = A ^k , ( э i ₀ • э_{к 0}) = A . Данное соотношение выполняется, если в качестве времени - подобных ортов выбрать э₀₀= э 0 = и , где и - 4-скорость частицы вещества, движущейся с 3-скоростью в = { в ,0,0 } по мировой линии С относительно фиксированного пространства-времени с 4-реперами { э. } , { э ¹ } . Выбранные координаты подвижного 4-репера {э_;.₀} входят в обобщенное преобразование Лоренца для координатных дифференциалов dx , dx₀ : dx i = ( э q ) dx^k ; dx¹ = ( э ₀) dx_o^k . Следовательно, ( э^ ) , ( э^ ₀) - матрицы Лоренцевых преобразований. При этом проектирование одних орт на другие определяется следующим образом: ^э 0 = ( ^э 0\ ^{э k} , ^{э 1} = ( ^э k о ) i ^э k , где ( ^э 0 )_к = ( ^э 0 • ^э k )^и ( ^э k o ) = ( ^э . о • ^{э k} ) •

Здесь особо следует отметить, что в последних записях типа (э^ ) внешний индекс к управляется метрическим тензором g_mк , а внутренний i - тензором п •

Подвижный 4-репер сопутствующей системы отсчета конкретизируется выбором для него следующих 4-векторов [50]:

{ ^э 1 0 } = ( B , p , q , u ) ^;   { ^{э 1} о } = ( ^- B , ^- p , ^{- q} , u ) .

Здесь и - 4-скорость частицы континуума движущейся относительно фиксированного пространства-времени по мировой линии С с 3-скоростью в = {в,0,0}, так что координаты ui =(в/,0,0,Y),U =(—в/,0,0,Y),Y = (1 — в2) ’2. В выражении (50) В - 4-вектор нормали к С с координатами Bi =( Y,0,0, вY), В =(—Y,0,0, вY) . Орты p, q в сферической системе координат фиксированного пространства-времени (r - радиус-вектор, 6 - азимутальный угол) задаются следующими координатами:

p i =1 0,1,0,0 | ; Р 1 =| 0, - 1,0,0 | ; q i =| 0,0,—

,0 J ; A=\ 0,0,--1-,0

У       V        r sin 6

V r     )       у r     /       V r sin 6

Преобразование произвольных векторов и тензоров к системе подвижного 4 -репера по формулам Лоренца имеет вид:

A = A m ( э . 0 )‘ ; T ki = t ; ; ( э , . ) ' ( э m „ ), .                               (51)

При этом, согласно [50], компоненты эт0 имеют вид:

( ^э 10 ) 1 = - B 1 = B 1 ,   ( ^э 10 ) ⁰ = B o = B 0 , ( ^э 20 ) 2 = Р 2 , ( ^э з0 ) ³ = q 3 , ( ^э 00 ) 1 =- U 1 = “ 1 , ( ^э 00 ) ⁰ = и 0 = и ⁰.

Следовательно, преобразование (51) фактически сводится к разложению величин A, Tik по 4- векторам подвижного репера и тем самым величины Am, T0n, Tm представляют собой скаляры. Это важное свойство 4-репера используется в задаче релятивистской инерциальной навигации.

Ковариантные производные компонент 4-вектора

DAi / dT = A к = дA / дт + ГAmA= = A + FA Am k            , k       k            km           k      km в фиксированном пространстве-времени определяются через производные от скаляров Am и ковариантные производные от компонент реперных 4-векторов (э.0)k. Ковариантные производные от компонент (э.0 )k имеют вид [50]:

B k = U ( bu k - GB k ) - B ( pp> + q q ) ; p k = pi- ( B¹ B i - и^xu ') - c^ q Q k ;

q k = q7 ( B¹ B ^{- uи} ') ⁺ c"tg ^ p^q ; 4 = B ( ^bu k ^- GB k ) - у ( pPk + q q k ) •

Параметры b и G имеют физический смысл модуля 4-ускорения и 4-скорости деформации b = у³ ( в + вв ') , G = / ³ ( в + вв ) = P b + Py , где в = д в / д г , в = др / дт - частные производные 3-скорости в = { в ,0,0 } в фиксированном пространстве-времени. Таким образом, эффекты неинер-циальности движения вещества описываются членами, содержащими b и G , а остальные члены, пропорциональные r ^{- 1} , описывают геометрические факторы. Максимальное число производных (52) может быть 64, так как представляют собой 4-тензоры 2-го ранга.

Правила изменения 4-репера {э.₀} при пространственно-временных перемещениях подвижного 4-репера вдоль мировой линии С определяются через введенные ковариантные производные 4-векторов. Соответствующие абсолютные производные 4-вектора А и скаляра р по направлению координатных линий сопутствующей системы отсчета { х ' } определяются с помощью соотношений

^Ak      mm k    5ф

i  =(э10 )  A \m ; p i = ф,г0 =(эi'0 )

дx0               1д

„ dф      ф п Ф<Р

Здесь р = 9 —; р =--+ в^— •

,T0      dT     ,х 0    9

Из соотношений (53) можно вычислить, используя (52), абсолютные производные компонент подвижного 4-репера {э. A при перенесении его по координатным линиям { х ' } [50]. Из этих формул следует, что при таком переносе (перенос Ферми - Уолкера) сохраняется свойство ортогональности. Так, орты 4-репера {э.A по общей формуле A = A э.₀= A 1 B + A 2 p + A 3 q + A 0 и по (50) можно представить в нем само при A =э _г 0 . В этом случае из (50) следует B 1 = 1, p 2 = 1, q 3 = 1, и 0 = 1 .

Следовательно, это означает в локальном смысле сопутствующий 4-репер (Д = 0) . Все остальные частные производные скалярных величин тождественно обращаются в нуль, что обеспечивает сохранение основного свойства соответствующей системы (в = 0) • Таким образом, полное определение сопутствующей системы отсчета дается соотношениями (50), (52).

Наряду с заданной системой координат наблюдателя xⁱ с тетрадой базисных векторов ∋ и сопутствующей системой координат с тетрадой базисных векторов ∋ ˆ (отвечающей заданному или искомому семейству мировых линий) в ОТО используются и некоторые, специальным образом определенные тетрадные поля базисных векторов.

Одно из таких определений собственной тетрады в точке мировой линии рассмотрим в связи с использованием в задаче релятивистской инерциальной навигации.

Пример 6. Пусть С – некоторая ненулевая мировая линия точки М , которая движется с конечным ускорением и индивидуализирована условиями ^ = const . В каждой точке данной мировой линии С определена некоторым способом ортонормированная тетрада е_а , е₀ = и . Базисные векторы тетрады е_а в близких точках M и M ’ данной мировой линии связаны, согласно примеру 3, между собой бесконечно малым преобразованием Лоренца

ea (M') = (^ + toads) eb (M) или de; = ^beb

Поскольку, согласно примеру 3, в системе координат наблюдателя с базисными векторами ∋ компоненты матрицы ||toj|| имеют вид to = aU = aU , то компоненты ek базисного вектора еа в базисе эк (еа = ek э^ ) , согласно (54), определяются в виде e a = (akuj -ajuk\e .. (55) ds aj

Согласно Части 1, выражение (55) определяет перенос Ферми – Уолкера.

Для каждой точки М данной мировой линии С наряду с тетрадой Ферми – Уолкера e можно локально ввести поле тетрад э. , значение которого совпадает в точке М с тетрадой е_а : э.|= е^_м и которое постоянно вдоль геодезической, касательной к мировой линии С в точке M : d э. / ds = 0 . Для геодезической линии, проходящей через точку М данной мировой линии и касающейся ее в этой точке, тетрада ∋ является, таким образом, тетрадой Ферми – Уолкера.

В ОТО локально определенную тетраду ∋ можно рассматривать [50, с. 86] в каждой точке сопутствующей (см. пример 5) системы отсчета как локальный инерциальный базис, свободно (с ускорением, равным нулю) падающий в гравитационном поле. Локально определенный инерциальный базис э. называется собственной тетрадой в точке М. Приращение собственного времени d r - одно и то же относительно тетрад базисных векторов e и ∋ .

Векторному базису ∋ в точке М соответствует, таким образом, локальная инерциальная система координат: начало этой системы координат движется по геодезической с ускорением, равным нулю (так как d э0 /ds = 0), ее скорость и в точке М равна скорости индивидуализированной точки М, а du / ds = 0 . Так как пространственные векторы базисов еа и э^ при переходе от одной точки мировой линии к другой сохраняют свою ориентацию (с точки зрения наблюдателя в базис ∋ ) в трехмерном пространстве, то для обоих 3-реперов в трехмерном пространстве их ориентация одинакова во всех точках мировой линии. Различие базисов e и ∋ обусловлено только поступательным движением триэдра базисных векторов ∋ относительно триэдра базисных векторов ∋ наблюдателя. Если V – 3-мерный вектор скорости этого поступательного движения, то тетрады базисных векторов ∋ и ∋ связаны преобразованием Лоренца.

Определенные таким образом локальные тетрады собственных базисных векторов позволяют установить связь между вектором 4-ускорения и используемым в ньютоновой механике 3-вектором ускорения. Такая связь установлена в связи с задачей релятивистской инерциальной навигации.

Преимущество сопутствующих и собственных систем координат связано с независимостью физических соотношений от выбора системы координат наблюдателя. Для наблюдателя соответствующие соотношения зависят от выбора системы координат (самого наблюдателя) и получаются с помощью тензорного преобразования от известной сопутствующей системы к известной системе координат. Ряд особенностей кинематики релятивистских эффектов в таких системах рассмотрены в Части 1 настоящей работы.

Решение задачи инерциальной навигации [32] основано на использовании показаний инерциальных приборов в сопутствующей системе и состоит в определении различных соотношений с последующим их пересчетов по правилу тензорных преобразований к известной заданной системе отсчета наблюдателя. Так, например, ускорение и различные другие векторные или скалярные величины, определенные наблюдателем в синхронных сопутствующих системах координат можно пересчитать в данном римановом пространстве для любых заданных наблюдателей с помощью алгоритмов, разработанных в теории инерциальной навигации [20, 32].

Следует отметить, что зависимость результатов измерений не только от механических состояний изучаемого объекта, но и от состояний наблюдателя присуща не только теории относительности. Так, в квантовой механике постулируется, что физическая интерпретация получаемых результатов неотделима от наблюдателя. Однако некоторые общие физические положения об инвариантности получаемых физических выводов и результатов относительно вспомогательных средств измерений сохраняются именно благодаря указанным тензорным преобразованиям.

Поскольку в исследуемой задаче релятивистской инерциальной навигации существенно используются понятия 4-скорости и 4-ускорения в сопутствующих системах отсчета, то в первую очередь отметим некоторые физические особенности используемых характеристик.

Определение и особенности 4-скорости и 4-ускорения в сопутствующих системах отсчета

Из определения вектора 4-скорости и правила преобразования компонент векторов выражения для контравариантных и ковариантных компонент для 4-скорости в сопутствующей системе координат имеют следующий вид [20, c. 65]:

k kk \^-^ _ek ax ^0 \^-^ s \-^ u = § i u = ( g 00 ) 3₀; u = 0, и = ( g 00 ) ; и_k = g_ьи = ( g 00 ) g_k о

.

Из множества сопутствующих систем координат, соответствующих одной и той же системе отсчета, можно выбрать такую систему, в которой g00 = 1. Тогда выражения для компонент 4-скорости в сопутствующей системе координат примут вид U1 = ^0, uii = g^.о. Как ранее показано, в любых системах координат в каждой точке можно рассматривать псевдоримановы 4-мерные пространства с ненулевым собственным временем т в канонической сопутствующей метрике и координатными тетрадными базисами {э.}, i = 0,1,2,3 в виде ds2 = c2dт2 + 2cga0 (£",T)d^^dT + gap (?,т)d^L.

В каждой индивидуализированной точке с координатами { d " , т } в римановом пространстве можно ввести соответствующую (56) каноническую глобальную метрику с определением глобальной временной координаты т и различные системы отсчета с тетрадными базисами э₀ = и и э ¹ в каждой точке пространства или на отдельных мировых линиях С и рассматривать различные системы отсчета наблюдателя К [8, 20]. Тогда в метрике (56) на сопутствующих линиях С для векторов u выполняются в компонентах и ⁰ = 1, и " = 0, и ₀ = 1, и_а = g_{a (} ^ "“ , т ) и в базисах э k на линиях С имеем u = ^Э 0 = ^Э 0 ⁺ g a 0 ( Г , т ) э " . Данное выражение справедливо в разных 4-мерных пространствах Римана, в которых поле 4-мерных скоростей и при и = э₀ и соответствующие мировые линии С образуют различные семейства с наложенной метрикой вида (56) в координатах Лагранжа { ^‘ , т } [40]. В этом случае относительное ускорение a (относительно системы отсчета наблюдателя К ) в виде частной производной по собственному глобальному сопутствующему времени т имеет вид

д -и

У = a дт

' rel = £ ( g a 0 ' )

д э0+--- дт

.

и определяет вектор относительного ускорения на мировых линиях С .

Из (57) следует, что вектор а_ге1 всегда перпендикулярен к единичному базису э ⁰ = и , так как вектор и = э₀ единичен и направлен по касательной к С . Согласно (57), векторы относительного ускорения можно выразить через переменные компоненты метрики g_{k 0}( ^ “ , т ) и контравариантные векторы базиса э ^k ( ^ “ , т ) , которые рассматриваются в точках заданных или искомых мировых линий С .

Пример 1. Движущаяся ортонормированная тетрада базисных векторов e_a ( е ₀ = и ) , связанная с точкой, движущейся с произвольным (но конечным) ускорением, каждый из векторов которой переносится вдоль мировой линии по Ферми – Уолкеру, как известно называется репером (тетрадой) Ферми – Уолкеру. Перенос Ферми – Уолкера пространственных базисных векторов можно осуществить, связав их с малыми гироскопами, оси которых направлены по векторам e _a . Вдоль мировой линии наблюдателя некоторые коэффициенты связности системы координат, связанной с тетрадой Ферми – Уолкера, можно вычислить, используя правило переноса локальной тетрады базисных векторов e _a и выражения для компонент to⁴ (см. приведенный пример выше из предыдущего раздела).

Для компонент вектора 4-мерной скорости и 4-мерного ускорения в локальной сопутствующей системе координат, связанной с тетрадой Ферми - Уолкера, имеем и " = 0, и ⁰ = 1, a ⁰ = 0 . Из формул для коэффициентов связности Г '_яи (см. Часть 1) в точках мировой линии С следует Г0₀ = Г f ₀ = 0, Г0₀ = а_а , Г " = а " . Остальные независимые коэффициенты связности можно определить, используя для продолжения тетрады в окрестность линии С параллельный перенос по пространственным геодезическим (они будут во всех точках линий С равны нулю).

Таким образом, в сопутствующей системе координат на ненулевой мировой линии С, индивидуализированной условиями ^“ = const, из определения 4-мерного ускорения и приведенных результатов следует выражение a = гоо э..                                                 (58)

В (58) учтено, что на выбранной мировой линии С выполняются равенства d Ча      а     -О  ,

---— = 0, и- = 0, и = 1 . Используя выражение для символов Кристоффеля через компоненты ds ²

метрического тензора в сопутствующей системе координат, из (58) получим следующее выражение для вектора 4-ускорения

1      д -^j j⁰

a = " -  / c    дт

∋ ˆ _i .

Пример 2. Дифференцируя по т равенства зисе ∋ ˆ ⁱ сопутствующей системы координат и в

и = э₀ = э ⁰ + д_а0 ( ^^а , т ) э ^а вдоль С в голономном ба-неголономном ортонормированном базисе eⁱ можно

получить

М. = -    ■ g - к =„ «L   g  „-

k 0 k 0

дт       дт дт         дт дт

В метрике (56) в каждой точке рассматриваемой мировой линии С верны следующие инвариантные соотношения [49, с. 185]: 1) д ₀₀ = д ₀₀ = 1 , поскольку по построению ( и =э₀ = э ⁰ + д_{а 0} ( ^^а , т ) э ^а ) _{0    0         а}        д э_п    д е ⁰

имеем э0 = е =э° + да0 э , при ---0 ^---; 2) из фиксирования типа риманова пространства следу- дт   дт

, д эк             дек                     . д эк       дек   п ет     = -г оi э ; — = -г оi e , поэтому дк о — = дк»— = 0.

дт            дт                      дт       дт д^-аа а  дд 0 а

Из приведенных условий следует выражение ---0 еэ =---0 е . Перпендикулярность ускоре- дт       дт ния к вектору э0 выполняется, так как э0 = е0 , а векторы еа перпендикулярны к е0 в силу ортонор-мированности. Таким образом, в сопутствующей лагранжевой системы (в соответствии с определением собственной системы координат) на любой линии С, отвечающей уравнениям ^а = const, для относительного ускорения имеем

a

^д g - а о

— а

В заключении отметим, что сопутствующие координаты и соответственно их канонический вид вместе с глобальны собственным временем являются выделенными системами отсчета. Переход от соответствующих моделей в сопутствующих системах отсчета на другие системы отсчета и составляет сущность задачи инерциальной навигации [19, 20, 32].

О связи 3-мерного и 4-мерного ускорений в собственной и в тетраде Ферми - Уолкера

Рассмотренные ранее локальные тетрады собственных базисных векторов позволяют установить связь между вектором 4-ускорения и используемым в ньютоновой вектором 3-ускорения. По определению вектор 4-ускорения a ортогонален вектору 4-скорости u . Поэтому в локальной собственной ортонормированной тетраде базисных векторов ∋ (см. выше введенные определения) вектор a имеет (при условии э₀ = и ) только пространственные компоненты

α a= a∋α

При указанном способе введения собственной тетрады базисных векторов компоненты вектора 4-ускорения в тетраде Ферми – Уолкера также будут равны aα . Так как в ньютоновой механике компоненты вектора 3-ускорения a точки М (при ξα = const) относительно инерциальной (локально dϑα     α

∋  (ϑ – 3-скорость точки М dt α

определенной) тетрады ∋ определяется равенством a=aα ∋ относительно триэдра базисных векторов ∋ ), то в собственной тетраде базисных векторов ∋ (вве- денной в окрестности точки М), 3-скорость ϑα на мировой линии С индивидуализированной точки равна нулю. Тогда du dui1 dui a=    =     ∋i=ai∋ =      ∋ .                              (63)

ds ds          c d τ

ϑα

Из (63) с учетом соотношений u ^α = , N c ² - ϑ ²

0c                 α u=          следует a c2 -ϑ2

a ^α c ^{2 .}

Из данного

выражения следует, что компоненты вектора 4-ускорения в локально определенной собственной тетраде ∋ ⁱ совпадают (с точностью до постоянного множителя c ^{- 2} ) с компонентами вектора 3-ускорения. Учитывая (59) получим в результате

α           ∂ g ˆ _{j 0}

aα ∋α=cgˆij∋

∂ τ

Скалярное умножение обеих частей (64) на ∋ ˆ дает соотношение следующего вида:

∂∂gˆτk0 = 1caα(∋β∋ˆα).

Из соотношения (65) следует:

∂gˆ00 =0,  ∂gˆα0 =1aβ(∋β∋ˆα).

∂ τ ∂ τ c

При выводе (66) учитывалось, что по определению ∋ перпендикулярны ∋ ˆ при условии, что g ˆ = 1 . В общем случае имеет место неравенство g ˆ _α ≠ 0 , т.е. в сопутствующей системе координат ∋ ˆ не ортогональны ∋ ˆ .

Для исправления данного факта вводят триэдр базисных векторов сопутствующей системы координат следующего вида:

∋ _α = ∋ ˆ _α - g ˆ _{α 0} ∋ ˆ₀.                                        (67)

Для данной мировой линии С , индивидуализированной условиями ξ^α = const , с помощью вектора ∋ ˆ = u , направленного по касательной к мировой линии С .

Из (67) следует, что (∋∋ˆ ) = 0 , т.е. триэдр базисных векторов ∋ принадлежит элементу 3-мерного пространства V , локально ортогонально данной мировой линии С. При этом вектор ∋ представляет собой проекцию вектора ∋ˆ  на подпространство, локально ортогональное мировой линии С. Для векторов ∋ и ∋

справедливы равенства

ˆ

У ^а Р)  \ а р)

; в результате соотношения

в (65) записываются как

^^ = 1 a в (^а Эр ).                               (68)

дт c

Соотношения (65) и (68) применяют при решении задачи инерциальной навигации в СТО и ОТО.

Примечание . В связи с выражением (59) отметим, что система отсчета п^а = f ^а ( 5 ) , П = f ( 5° ) , определенная условиями g ^₀ = 0, g ₀₀ = 1 , называется синхронной . Для семейства мировых линий в синхронной системе отсчета при П = const может быть введено глобальное голономное собственное время т = t . При выполнении условия интегрируемости имеем д g а       дg _п д g в о

—^{0 0} = 0, —0 °-- L_ = о . Из (59) следует равенство a = 0 на мировых линиях рассматриваемого

дт       д5в   д5а семейства. В этом случае мировые линии, индивидуализированные условиями па = const, являются геодезическими [20].

Приведенные определения и результаты позволяют рассмотреть задачу релятивистской инерциальной навигации, которая имеет решение в рамках СТО, в системе координат Ферми в СТО, в системе отсчета произвольного наблюдателя в СТО и ОТО.

Приложение: Геометрия параллельного переноса вектора и тензора

Напомним некоторые необходимые сведения об операциях из тензорного анализа. Если Aⁱ и B^k_m - тензоры то Ci_jtт = AiB^ - также тензор, порядки ко- контравариантности которого равны суммам соответствующих порядков двух первых тензоров. Эта операция носит название умножение тензоров; она также инвариантна относительно преобразования координат. Рассмотрим смешанный тензор A^ij . Выделим компоненты, у которых один из индексов ковариантности совпадает с одним из индексов контравариантности, и составим их сумму A ^ = A ^ 1 +-----+ A in . Совокупность величин A ^ ^

является тензором, у которого порядки ко – контравариантности на единицу ниже, чем у исходного тензора. В данном случае А ^ представляет собой смешанный тензор второго порядка - ковариантный относительно индекса k и контравариантный относительно i . Эта операция называется свертыванием. Если порядки ко – контравариантности одинаковы, то можно выполнить полное свертывание, результатом которого является скаляр, или инвариант, данного тензора. Так, двойная сумма A^ служит инвариантом тензора A^j . В качестве простого пример имеем 5 ^ = n . Несколько более сложным примером является свертывание произведения gyg^ . Имеем g_iag^ka = 5 k , gapg ^ = 5 ^ = n • Сочетание умножения и свертывания позволяет осуществить особые операции, называемые поднятием и опусканием индексов. Пусть A - ковариантный тензор третьего порядка. Составим произведение A_ijag^ka и, положив a = в , выполним свертывание. Полученный таким образом тензор A_ijag^ka имеет второй порядок ковариантности и первый порядок контравариантности. Его обозначают обыкновенно символом A^k ; один из индексов оказался поднятым. Аналогично, умножив тензор B ^ijk на g и произведя затем свертывание, можно образовать тензор B^ij , опустив один из индексов исходного тензора. Это дает возможность изменять строение тензоров: по заданным ковариантным компонентам вычислять смешанные или контравариантные компоненты и наоборот. В частности, символы Кронекера можно рассматривать как результат поднятия одного из индексов ковариантного метрического тензора или как результат опускания одного индекса контравариантного тензора.

При задании двух тензоров одинаковой структуры в одной точке пространства вопрос об их ра- венстве решается путем непосредственного сравнения компонент: тензоры считаются равными, если их соответствующие компоненты одинаковы. Если же тензоры заданы в различных точках простран- ства, то при применении криволинейных координат вопрос об их равенстве или неравенстве требует

M_x ( х^г_х ) и M ₂ ( х\ ) заданы векторы с

дополнительного рассмотрения. Пусть, например, в точках контравариантными компонентами yi и yi соответственно. Поскольку координатные векторы в указанных точках различны, непосредственное сравнение компонент не может служить признаком равенства или неравенства векторов. Предварительно необходимо ввести в одной из точек местную (локальную) систему координат, выбрав ее так, чтобы координатные векторы этой системы совпали с координатными векторами в другой точке. Если при этом соответственные компоненты рассматриваемых векторов окажутся одинаковыми, то и сами векторы равны. Такое качественное определение равенства применимо и для тензоров (любого порядка и структуры). Если два тензора одинаковой структуры, заданные в различных точках пространства, отвечают этому определению, то их называют равными; каждый из них представляет собой результат параллельного переноса тензора из одной точки в другую. Для определения равенства или неравенства тензоров, заданных в различных точках, нет необходимости в фактическом выборе местной (локальной) системы координат. Достаточно найти в общем виде закон изменения компонент тензора при его параллельном переносе из одной точки пространства в другую.

Рассмотрим некоторые особенности операции параллельного переноса тензора.

Особенности геометрии параллельного переноса вектора. Рассмотрим, прежде всего, вопрос о бесконечно малом параллельном переносе контравариантного вектора. Пусть вектор y i задан в точке M (xi) . Требуется определить, какие приращения приобретут компоненты этого вектора при его параллельном переносе в точку M‘(xi + dx ). В точке М координатные направления dr определяются единичными векторами e = —-, где r - радиус-вектор точки М относительно произ-дxi вольно выбранного начала. При переходе к точке M' координатные векторы изменяются на

, дei de,. = —- i   дx"

индексов

а а     д 2r                   Sei                    „ dx = —:---dx . Величина —- представляет собой вектор, симметричный относительно dxi дxa                 дxj i, j. Разложив его на составляющие, направленные вдоль координатных линий, можно записать

j—’ а _аа

'у =1 Ji.

Sei T^ a ,-a iT - = ^Г y^a , ^{где г} у дx^J

Для определения

– коэффициенты разложения, отвечающие условию симметрии

этих коэффициентов дифференцируем известное соотношение

g j =^{( e} i ,e j ) :

Умножив    равенство

de.       i , yyj,ek | = Г-' (ea,e. ) = gakГ".

д x^j     )

перестановку индексов, получим

виде:

dgij = kI дxv д

(   de,

⁺ e i , TT , e j

дx

.

(П.1)

de. а_

—- = Г1еа     скалярно на вектор     ek, получим дxj

Вводя обозначение g_aкГ“. = г _к и выполнив соответствующую

(Sei соотношение I —^- ,ej I = Гй j. Поэтому (П.1) можно переписать в

^дg y ₌(дe_K д x^k   la x^k ,

(   de,    )

^{+ e} i, "^k ^{,e j}

v  dx )

= Г ik , j +Г jk , i

(П.2)

С помощью этого соотношения можно найти коэффициенты Г^. к , после чего искомые коэффициенты Г * вычисляются на основе ga АГ" = Г к . Круговая перестановка индексов в (П.2) позволяет дgjk   д gy R составить выражение для производных     и     . Вычитая из суммы этих производных величину дxi     дxJ

(П.2), получим

Г... = ij , k

^{1 ( д} g ik   ^{д g} jk

2   д x^j

дx

—

gij дxk

.

(П.3)

Для вычисления коэффициентов  Гk g«Г в = Г/ а . Умножив это равенство

используем ранее установленное соотношение на  gak  и просуммировав по а , получим gapgalkГiJ = ^ГiJ = gakГija , откуда непосредственно следует Г У = g"Гу,а • Величины Гу,к и Гу называются символами Кристоффеля первого и второго рода соответственно. Символы симметричны относительно индексов i, j и являются однородными линейными функциями производных от ком- понент метрического тензора по координатам. Символы Кристоффеля не являются тензорами, но входят во многие соотношения тензорного анализа.

de в

При решении задачи о параллельном переносе вектора в соотношении --- = Г^e „ приращение

5ха вектора с. представляют в виде dez = Гв e^dx“ . Таким образом, координатные векторы в точках M и M‘ соответственно равны ez и ez +Гв e^dx“ . Как известно, вектор равен сумме произведений его ковариантных составляющих на единичные векторы координатных направлений (см. рис. П.1).

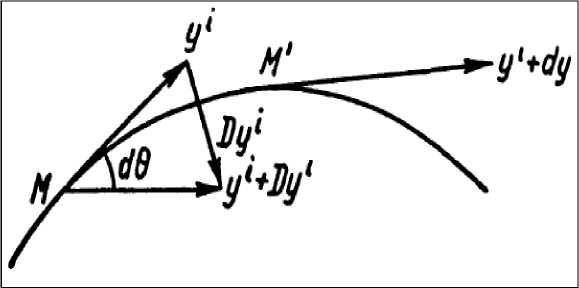
Рис. П.1. Параллельный перенос вектора

Поскольку составляющие в точке M, M' соответственно равны yi и yi + dy‘, то условие параллельного переноса выражается уравнением ezyi =(e, +Гв e^dxa )(y1 + dy1) . С точностью до бесконечно малых первого порядка имеем Гв e^yldxa + etdy1 = 0, или (Гypd“dx+ + dy1) ez = 0 , откуда, ввиду произвольности системы координатных векторов, следует dy‘=-Г‘ав y“dxp.

(П.4)

Выражение (П.4) определяет приращение контравариантных компонент при параллельном переносе вектора в бесконечно близкую точку. Выясним, как при параллельном переносе изменяются ковариантные компоненты вектора. В точке М эти компоненты определяются, как знаем, в виде yi =( У, ei) . В точке M' значение ковариантной компоненты y + dyf равно скалярному произведению вектора y на координатный вектор ez +Гв e^dxa. Следовательно, y+dy=( y, e )+га (y, e в) dxa, или dy ^-Г,а ypdx“.

(П.5)

Примечание . Сравним рассмотренные процессы параллельного переноса вектора в плоском и криволинейном пространстве. Зададим векторы V_р ( x ) и V^ ( y ) на рис. П.2 в двух пространственновременных точках. Между двумя векторами есть различие А V_ц , равное

А V, =   dVM   +     ^V^

различие в одной изменение тангенциального системе координат        пространтсва

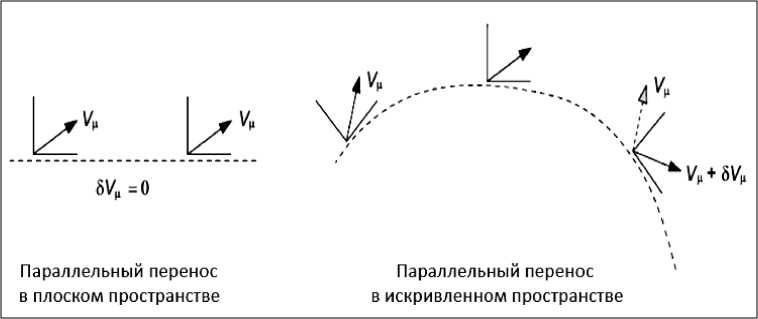
Рис. П.2. Параллельный перенос вектора в плоском и криволинейном пространстве

В плоском пространстве ЗУ„ = 0 и имеем в результате AV/z = dV„ = (5^V, J dxa , т.е. ковариант-ц                                 ц ц a ц ная производная эквивалентна частной производной. В криволинейном пространстве на инфинитезимальном расстоянии между x и у можно принять величину ЗУ линейной функцией от У^ и dxa , т.е. ЗУ = Г^аVvdxa , где Г^ является аффинной связностью.

Поэтому имеем:

A V, = dV, + ЗУ, =^

(8„V, +r;„) dx ковариантная производная

( криволинейное пространство )

д^ V^dx ^a       (плоское пространство)

Найденные законы изменения ко- и контравариантных компонент при параллельном переносе вектора нетрудно обобщаются на случай тензора любой структуры. Так, при переносе в бесконечно близкую точку смешанного тензора третьего порядка его компоненты приобретают приращения dX* = —Г^Хв dxa + Г * X^dxa + Г * Х^•               (П.6)

jk         ар jk           ja p k            a k j p

Применим операцию параллельного переноса к метрическому тензору.

Параллельный перенос тензора . Пусть в пространстве задано поле тензора g . Если в точке

M ( x ^a ) компоненты этого тензора равны g_ip , то в точке M¹ ( x i + dx¹ ) они определяются формулами

5gj a.a\ g.. + dg.., где dg.. = —- dx . Произведем параллельный перенос тензора g.. из точки M (x ) в

J      J           J   дxa точку M‘(xi + dx1). Приращения компонент, обусловленные этим переносом, обозначим Agtj..

Agj = ( gjpg * Г a + gpg Р'Г№, ) dxa = (З; Г a, + S'Ta, ) dxa = (Г aj + Г „,,) dx‘.

^д § ij  , a

= dg , совпадая с дифференциалом,

Согласно (П.2), искомое приращение равно Ag.. = —-dx дxa обусловленным различием координат в точках M, M1. Это значит, что поле метрического тензора можно рассматривать как результат параллельного переноса этого тензора из какой-либо одной точки во все другие точки пространства. Такой же особенностью обладают тензоры gi и 31 . Так, приращение смешанного тензора 31, вызванного его параллельным переносом, равно

Mj = -rlap5Pdxa + Г%5^с“ = 0 , что совпадает с дифференциалом этого тензора, имеющего одинаковые значения компонент во всех точках пространства. Таким образом, рассмотрена задача о параллельном переносе тензора в бесконечно близкую точку.

Рассмотрим теперь задачу о параллельном переносе вектора и тензора на конечное расстояние. Допустим, что некоторый контравариантный вектор задан в точке M ( х " ) своими компонентами y i . проведем через эту точку непрерывную линию, заданную уравнением х¹ = х¹ ( т ) , где т - параметр, принимающий для точки М значение т ₀. Требуется параллельно перенести вектор вдоль данной линии. Соотношение (П.4) определяет приращение компонент вектора при его параллельном переносе между двумя бесконечно близкими точками кривой. Разделив это соотношение не приращение параметра d т , отвечающее переходу между указанными точками, получим:

dy      dx

(П.7)

— + Г ' _в---у^а = 0 .

dт      dт

Входящие в (П.7) символы Кристоффеля выражаются через составляющие метрического тензора и их производные по координатам. Для данной линии эти символы являются определенными функциями параметра т , зависящими от уравнений линии. Теми же уравнениями определяются произ-dxe              , х водные     . Равенства (П.7) составляют систему линейных однородных уравнений первого порядка относительно величин у1. Поскольку при т = т величины у1 принимают заданные значения yi , эта система имеет единственное решение, однозначно определяющее параллельный перенос вдоль линии.

Приложение 1: Бусты группы Лоренца и вращение Томаса - Вигнера

Рассмотрим необходимые основные понятия группы Лоренца и связь с вращениями (поворотам) Вигнера. В пределах модели специальной теории относительности (СТО) при переходе от нерелятивистской к релятивистской механике группы симметрии пространства-времени переходят из группы Галилея в группу Пуанкаре. Группа Пуанкаре состоит из преобразований пространства-времени, вращений и бустов Лоренца. Здесь остановимся на понятии бустов группы Лоренца.

Некоторые определения СТО и бусты группы Лоренца . Центральное место в группе Лоренца занимает определение так называемых лоренцевых бустов, которые для двух наблюдателей соотносят положение в инерциальных системах отсчета, движущиеся друг относительно друга с постоянной скоростью S . Предположим, что движение осуществляется вдоль оси x , Тогда преобразования между координатами систем отсчета принимают вид:

x ‘ = у ( x — S t ) , y ' = y , z ‘ = z , t ‘ = у ( t — S x I c ² ) .

(П1.1)

где у = (1 — S / c2)"%. Обозначим в = SI c и определим 4-вектор x“ =(x0, x1, x2, x3,) = (t, x, y, z) = (t,x ). Примем систему единиц, в которой Й = c = 1. Тогда (П1.1)

можно записать в виде

Г t '1		Г Y	— Yp	0	0 1	Г 1 1
f x	—	—ур	Y	0	0	x
y '	=	0	0	1	0	y
v z ' ?		v 0	0	0	1 J	V z J

(П1.2)

или в более компактном виде

x' = Л (S) x,

(П1.3)

где Л = Л (S) - буст в x -направлении. Часто бусты параметризуются, используя понятие быстроты, которое определяется как ^ = arctanhS, тогда в = arctanh^, у = cosh^, ув = sinh^, и матрица буста Лоренца в (П1.2) можно представить в виде

	г cosh ^  — sinh ^  0  0
	— sinh ^  cosh ^  0  0	.                               (П1.5)
Л(0 =	0     0   10 v    0         0     0  1 ?

Для частицы с массой m можно записать 4-момент

Р^ =( Р 0, Р1, Р2, P3 ) = ( E, Px , Py , Pz ) = ( E ( P ) ,P ) , где E ( P ) = 4P2 + m m где отношение для быстроты определяется в виде:

cosh^ =

У P2 + mm

m

sinh ^ = —. m

(П1.6)

Элементы матрицы общего вида буста Лоренца в направлении единичного вектора e = (ex, ey, ez ) = p / |p| задаются в виде [35, 36]

Лу (£) = 5у + (cosh£-1)ee, Лiо (О = лоi (£) = sinh А лоi (^) = c°sh£.

Группа Лоренца содержит также чисто пространственные вращения, которые имеют вид

" 1   0     00

(П1.8)

<0

где R ( 0 ) е SO ( 3 ) - матрица 3-мерного вращения. Множество всех 3-мерных вращений образует подгруппу группы Лоренца. Отметим, что в общем случае данный факт не выполняется для бустов группы Лоренца: они не образуют подгруппу группы Лоренца. Это нетрудно проверить с помощью комбинации двух бустов, которые для упрощения выберем вдоль x оси и z оси с быстротами 9 и ^ соответственно

	' cosh ^ x	- sinh 9 x	0	0 )		^ cosh 9		0	- sinh ^
Лх =	- sinh ^ x	cosh ^ x	0	0	,    Л	0	1	0	0	(П1.9)
x	0	0	1	0	z	0	0	1	0
	I    0	0	0	1 J		^- sinh z_	0	0	cosh ^ J

Произведение этих матриц дает

^ cosh ^ cosh ^ - cosh ^ sinh ^ 0 - sinh ^ ЛА = - sinh ^x cosh ^x 0 0 ,              (П1.10) zx 0 0 1 0 (-sinh ^z cosh ^x sinh ^ sinh ^. 0 cosh ^z J которое не имеет симметричный вид (П1.7). Однако, можно показать, что результатом является буст и матрица вращения

Л z Л x = R (т )Л,

(П1.11)

где R ( т ) - матрица 3-мерного вращения. Это выражение означает знаменитое вращение Вигнера или вращение Томаса – Вигнера (часто обозначаемое как TWR) и связано с прецессией Томаса.

Вращение Вигнера является следствием структуры группы Лоренца, которая характеризует релятивистскую природу пространства-времени. Приведенные соотношения показывают существование неколлинеарных бустов. Коммутационные соотношения отражают коллинеарность бустов и формируют подгруппу. Коллинеарность бустов со скоростями 9 и 9 подчиняются релятивистско

9 + 9

1 + 99

му правилу сложения скоростей 9 =

Вращение Вигнера является чисто кинематическим эффектом, которое не зависит от динамики поведения системы. В контексте квантовой механики вращение Вигнера приводит к неожиданным эффектам подобно прецессии Томаса и играет важную роль при исследовании запутанных состояний, когда квантовая система наблюдается из разных инерциальных систем отсчета.

Свойства вращения Томаса – Вигнера Рассмотрим три наблюдателя в инерциальных системах отсчета O , O ' , O ", где O' движется со скоростью Д относительно O и O" имеет скорость движения Д относительно O' . Согласно (П1.11), комбинация двух бустов Л ( Д ) и Л ( Д ) сопоставляет соответствующие системы отсчета O и O ", и представляет собой буст и вращение

Л(Д )Л(Д ) = R (го )Л(Д), (П1.12)

где R (to) определяет вращение Томаса - Вигнера с угловой скоростью вращения го . С точки зрения наблюдателя O система отсчета O" вращается с угловой скоростью вращения to , которая определяется в виде to sin 0 tan =----------,

(П1.13)

2 cos 0 + D где 0 определяет угол между двумя бустами, или, что эквивалентно, между векторами скоростей Д и Д , а параметр

D =       I ^ 2 + 1 1 , где Y i,2 = ( 1 - Д 2 Г.

IY1 -1/■-1)

Ось вращения определяется вектором n = Д х Д и ортогональна плоскости, определяемой векторами скорости Д и Д .

Зависимость вращения Томаса – Вигнера от угла между двумя бустами показана на рис. П1.1.

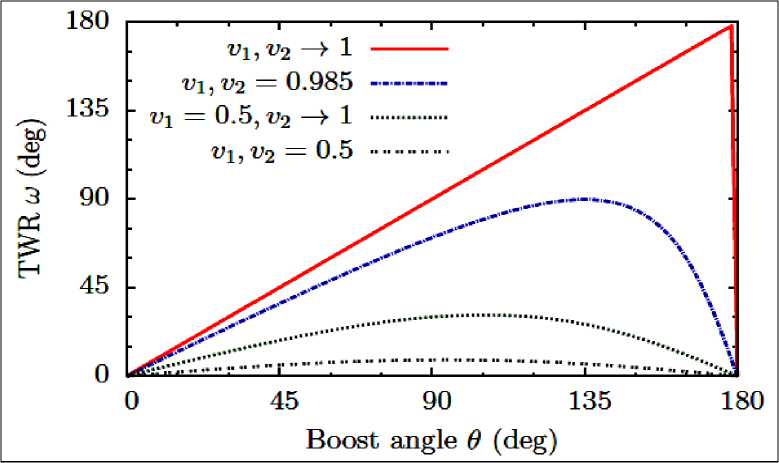
Рис. П1.1. Зависимость угловой скорости to вращения Томаса - Вигнера от угла 0 между двумя бустами (boost angle – угол буста) [51]

Отметим ряд интересных следствий.

Во-первых, для заданных двух бустов со скоростями ^ и ^ и углом 0 между бустами угол вращения Томаса - Вигнера возрастает до максимума 180 0 при стремлении обеих скоростей ^ и <9₂ к скорости света. Во-вторых, максимальное значение to ограничено малым бустом. Если ^ = 0.5 , то если <9 ₂ приближается к скорости света величина to меньше, чем в случае оба буста приближаются к скорости света. В-третьих, величина угла 0 , от которого зависит максимум вращения Томаса -Вигнера, зависит от значения скоростей ^ и <9 ₂: величина to стремится к максимальному значению 180 0 в случае противоположного значения или при стремлении ^ и ^ к скорости света. Перечисленные особенности играют важную роль, в частности, при исследовании поведения квантовых запутанных состояний в бустах систем отсчета. Исследование свойств вращения Томаса-Вигнера существенно зависит от сценария бустов или геометрии бустов, в частности, от триплета ( ^ , i 9₂ , 0 ) . Альтернативный вариант можно представить как ( ^ , ^ ₂, 0 ) в силу однозначного соответствия между скоростью и быстротой буста. Из (П1.13) при £ = ^ = ^ параметр to может быть определен как функция от £ и 0 в следующем виде:

to = 2 arctan

sin 0

_v cos ⁰ + D ( ^ ) _?

(П1.14)

где D(£) =

cosh ² ( ^ /2 ) sinh ² ( ^ /2 ) .

График на рис. П1.2 показывает аналогичную рис. П1.1 зависимость.

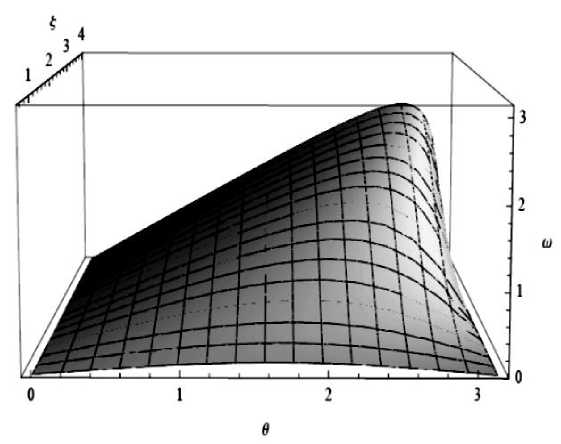
Рис. П1.2. Зависимость угловой скорости to вращения Томаса - Вигнера от быстроты £ и угла 0 между бустами [51]

Как и в случае рис. П1.1 множество малых бустов ограничивает максимум угла Томаса – Вигнера и поверхность на рис. П1.2 описывает возможные значения вращения Томаса – Вигнера при различных положениях на 0 - to плоскости и при фиксированных значениях быстроты £ .

Приложение 2: Кинематика поворотов и вращение Вигнера

Напомним предварительно некоторые сведения из кинематики поворотов. При повороте системы координат вокруг единичного вектора n компоненты вектора r(s) в начальной системе s и составляющие этого же вектора r(s′) в конечной системе s′ связаны равенством rα (s) = aβαr′β (s′), α,β=1,2,3,                            (П2.1)

матрица поворота a ^βα в координатах: ось поворота n и угол поворота φ имеет вид

aβα = δαβ cosφ+ nβnα (1 - cosφ) - eαβγnγ sinφ

При этом предполагается, что при поворотах вращается система координат, а сам вектор остаётся неизменным. Для матрицы поворота aβα справедливы соотношения ортогональности aβαaγα = aαβaαγ =δβγ                               (П2.3)

и равенства, которое называется равенством «уничтожения» в виде eαµνaµβaνγ = eµβγaαµ,  eαµνaβµaγν = eµβγaµα                      (П2.4)

Матрица вращения a ^βα ( t ) удовлетворяет уравнению

a   = -eαµνω′µaνβ,

(П2.5)

(П2.6)

dt где ω′ есть угловая скорость в системе s ′

ν ¹ αλν λβ ^{da αβ}

2          dt

Рассмотрим сейчас движение инерциальной системы отсчёта s ′ со скоростью v(t) относительно лабораторной системы отсчёта S . Если инерциальная система s ′ ориентирована таким образом, что преобразование пространственно-временных координат из S в s ′ является чистым бустом, то условно система s ′ ориентирована без поворота относительно S . Перейдём в новую лабораторную систему отсчёта S ^∗ , которая движется со скоростью u без поворота относительно S . В новой лабораторной системе начало отсчёта системы s ′ движется со скоростью (здесь c = 1) [42]

V _{1 - u} 2 _{v - u} ( 1 -   1 - u ² ) ( uv ) vu

(П2.7)

1 - uv           u ² ( 1 - uv )

Но преобразование из S ^∗ в s′ не является чистым бустом. Поэтому, чтобы получить систему координат s ′, оси новой системы отсчёта s ориентированные без поворота относительно S ^∗ (которая двигается со скоростью v(t) из (П2.7)) требуется ещё повернуть на некоторый угол φ вокруг некоторого единичного вектора n. Этот собственный поворот равен (см. [42, 43])

ntg ^A = n       ^A =                               .

2     1 + cos φ_A   ( _{1 +} >J 1 - u ² )( 1 + 1 - ϑ ² ) - uv ^.

Этот поворот следует называть вращением Вигнера. Если u мало, то

nφA =

1 + 1 - ϑ ²

ϑ ²

u × v.

(П2.9)

Матрица поворота Вигнера обозначается в виде b ^βα и (1) выглядит следующим образом:

rα(s)=bβαr′β(s′).

(П2.10)

Для малого угла φ матрица поворота (П2.2) имеет вид

bβα =δβα-eαβγnγφ =δβα+1-1-ϑ2 ϑαuβ -ϑβuα .             (П2.11)

^AA ϑ ²

По определению (П2.6) угловая скорость вращения Вигнера определяется в виде

αβ

ω ′ ^ν = ¹ e ^αµν b ^{µβ dbA}                                  (П2.12)

^A 2       ^Adt

Подставляя (П2.11) в (П2.12) получим, что она равна

d(nφA)  (1-1-ϑ2)

^dt       ϑ ⁴1 - ϑ ²

( vv ) u × v +

1 - 1 - ϑ ² ϑ ²

u × v .

(П2.13)

Рассмотрим теперь общий случай движения инерциальной системы k, которая имеет другую ориентацию относительно системы S, чем система без поворота s′. Другими словами, пусть компоненты вектора r(s′) в начальной системе s′ и составляющие этого же вектора r(k) в системе k связаны равенством rβ(s′) = aγβrγ (k).                                     (П2.14)

Подставив (П2.14) в (П2.10) получим, что результирующая матрица поворота между начальной системой s и конечной системой k есть a∗γα = aγβbβα.

(П2.15)

Таким образом, параметры системы отсчёта k , которая двигается со скоростью v и имеет ориентацию a ^γα относительно S , при чистом бусте со скоростью u преобразуются по законам (П2.7), (П2.15).

О связи между прецессией Томаса и вращением Вигнера Пусть в некоторой лабораторной системе S начало жёсткой системы отсчёта s′ движется поступательно (матрица вращения a ^{∗ βα} = δ^βα , т.е. без поворота относительно S) со скоростью v . Данная система отсчёта обладает собственной угловой скоростью равной частоте прецессии Томаса

Ω=

1 - 1 - ϑ ²

ϑ ² 1 - ϑ ²

v×v.

(П2.16)

После последовательно произведенных (в близкие моменты времени) бустов в мгновенно сопутствующие s′ инерциальные системы отсчёта новая прецессия Томаса системы s′ будет мала (из-за малой относительной скорости) и вся собственная прецессия Томаса будет относиться на счёт вращения Вигнера. Действительно, пусть в момент T+ΔT скорость системы s′ относительно S ста- ла v + Av. Перейдём в систему отсчёта, двигающуюся со скоростью u = v. Сделав замену в (П2.8) u ^ v, v ^ v + Av и учитывая, что угол поворота Вигнера ф мал, получим, что он равен

пф =

1 - 71 - s² s ²71- s 2

v х A v .

Очевидно, этот угол совпадает с собственной частотой прецессии Томаса (П2.16) умноженной на промежуток собственного времени. Это обстоятельство часто рассматривается как подтверждение того, что прецессия Томаса и вращение Вигнера являются разными названиями одного и того же физического явления. Но для произвольного (и даже для очень малого) буста необходимо проводить различие между вращением Вигнера и прецессией Томаса [43].

При совершении буста, движущаяся система отсчёта, имеющая прецессию Томаса, относительно новой лабораторной системы будет иметь комбинацию двух вращений: новой собственной прецессии Томаса и вращения Вигнера, которые в совокупности дают первоначальную частоту прецессии Томаса. Это обстоятельство можно пояснить также на примере, если произвести буст из S не в мгновенно сопутствующую систему отсчёта, а в произвольную со скоростью u . В новой лабораторной системе отсчёта S * начало отсчёта s ′ имеет уже скорость v* , связанную с v и и формулой (П2.7), а оси координат s′ испытывают дополнительное вигнеровское вращение (П2.8).

Следовательно, угловая скорость собственного вращения s′ в новой системе складывается из двух составляющих: новой собственной прецессии Томаса и вигнеровского вращения.

Пример: Инвариантные условия движения неинерциальной системы отсчёта.

Рассмотрим следующие 4 величины, состоящие из 4 компонент,

Л0 1 = (л00, Л0а ) =

1       9аv 71—9 ’71—9 ,

(П2.17)

где первый индекс у каждого символа отвечает за его номер, второй - за его компоненту, 9^а определяет 3-вектор скорости начала отсчёта неинерциальной системы. Данные величины удовлетворяют соотношениям ортонормированности

Л⁰¹Л ⁰ = 1, Л^ш Л ^а = 0, Л ™ Л ^в = -б “ ^э . (П2.18)

Отметим, что с математической точки зрения Л ⁰¹, Л ™ являются коэффициентами в преобразовании Лоренца из лабораторной системы отсчёта S : (T, R) в инерциальную систему s′: ( t , r′) в виде: T = Л^{а 0} r '^а +Л ⁰⁰ t , R ^e =Л “ ^в г ' “ +Л ^{0 e} t . Если рассматривать r '“ и t как параметры, то из определения величин Л ™ = dX^l I dr ' “ и Л⁰¹ = dX^l I dt следует, что они являются 4-векторами. Кроме того, при любом непрерывном преобразовании из группы Лоренца величины Л ⁰¹, Л ™ ( i = 0,1,2,3 ) преобразуются в величины той же математической формы (П2.17).

Как хорошо известно, нулевой вектор Л⁰¹ является время - подобным вектором 4-скорости начала системы s′, является единичным и касательным к мировой линии начала отсчёта неинерциальной системы s'. 4-вектор же Л ™ представляет собой пространственно-подобный орт а - й оси системы координат s′. Выражения

„ dXYi           1        dX™

W' г =Л ⁰. d ^, Q' ^Y =- ¹ e ^a ^ ^Y Л ^ d^— .

(П2.19)

dt            2          dt

В мгновенно сопутствующей инерциальной системе отсчёта эти произведения равны W'^Y = aS и Q' ^Y = e ^e^ aa “ ^e a ^ae , т.е. являются собственным ускорением и собственной угловой скоростью s′ соответственно. Данные уравнения будут выполняться в любой системе отсчёта в силу 4-векторности величин Л 0 i , Л^а . Это означает, что уравнения (П2.19) являются кинематическими, релятивистски инвариантными условиями движения данной неинерциальной системы с известными характеристиками. После дифференцирования (П2.17), представления в (П2.19) и использования равенств (П2.4) и (П2.5) в результате получим

W 'Y = aY

^    1 - У1 - s2

VT s ' // (1 - s ²)

(vv )sa

(П2.20)

Действуя аналогично, нетрудно получить из (П2.19)

Q'Y = aY“ 1 /1 S e““Yd“sv + to'Y.

(П2.21)

s2 (1 - s2)

Уравнения (П2.19) и (П2.21) после замены S^a = a ^eaS^e сводятся к уравнениям обратной задачи кинематики, как показано в [43].

Пример По своему смыслу формулы для определения собственного ускорения и собственной угловой скорости фактически описывают требования неизменности характеристик системы отсчёта s′ от бустов. Поэтому в новой лабораторной системе отсчёта S* и в старой системе S согласно принципу теории относительности собственное ускорение и угловая скорость системы s′ должны быть при подстановке (П2.7), (П2.15) равными. Произвольный буст можно рассматривать как композицию множества произвольных бесконечно малых бустов. Поэтому, чтобы показать в общем случае справедливость равенств (П2.21), (П2.20) достаточно доказать их выполнение для инфинитезимального преобразования Лоренца. Для инфинитезимального преобразования Лоренца из (П2.7) видно, что v* = V (1 + uv)-u, v* = v (1 + uv) + v (uv)

(П2.22)

При подстановке в выражение W '⁷ = a * ^Ya

ir    1 - V1 - s*2

V1 - s*^{2 +}s *² (1 - s )

(v* v*)s*a

формул (П2.22), а

также (П2.15) и (П2.11), после некоторых алгебраических преобразований получим, что математиче- ская форма величины W‘ не изменилась W’Y = aYa

sa    1 - V1 - s2Vr-s2 ^91 (1 - s2)

(vv )sa

, т.е. инвариантна.

Аналогично вышесказанному, подставляя (П2.6) и (П2.15) в (П2.21), дифференцируя и учитывая ортогональность матрицы Вигнера, которая аналогична уравнению (П2.3) получим, что

Q'Y

a *^{Y a}

1 - V1 - s*² s *² (1 - s *²)

e«as as*v + ю'*Y =

( a ^Y ‘ b W " ) ' -dT^- ! e°"® “ s"' + ¹ e ‘" ( a " ^{V b} W ) d! ( a "' b W ^Y ) = s ( 1 - s )               —               dt

^{( a}'^bW )

вкОЛ ^{1 - 1 -} - ^V

⁽ a ^b W ) V ² ( i - ^2 )

eay V V +1 ea1 [a*vaapbvXbex + aAVa“eea*V *V*v +i (e^17a^a^3)b-e + jea*a*vaapSvp

Во втором слагаемом учитывается первое из равенств "уничтожения" (П2.4) и после этого равенство (П2.12) приводит к результату в виде

O' ^;

* ²

¹ , У V ₄ e ^a * 9 V + ¹ e^{T Pv} a^b^b e ^- + ¹ e^a V"^{1 3} =

V ² ( i - v ² )             2        W W 2

ayP bWa

1 - 1- - V ² V * ( i _ _s *2) i - Vi - v*² V *² (1 - V *²)

e^V m9*v + to;wT + 1 ea* a^^a^3 =

W ₂

ea*V V + ^p

+ 1 e ^a * a^a ^ .

(П2.23)

Рассмотрим отдельно выражение стоящее в правой части (П2.23) в квадратных скобках. Подставляя сюда (П2.11), (П2.13), (П2.22) получим после некоторых вычислений, что

*2                 1_Jl_Q2

кP“  __22_____ p^a'^v Я 1 ,9* ^V ^rn’ P =2__—__ __ e^a'^vS * 9* ^V +

bW V* (i - V*2)e  V V + toW   V (i - V)e V V +

( i - ^ V ) 2

V4 (i - V2)

k p ,     (П2.24)

где вектор k , компонента которого входит в правую часть этого равенства, зависит от векторов v,v,u и равен k = V ²v x u + ( uv ) v x v - ( vv ) v^u + ^ v ( vxu ) J v . В [42, с. 8] показано, что k = 0.

Следовательно, из (П2.24) имеем [43]

bea i ;i V\ea‘vV*d*v W v*2 (i - V2)

новая прецессия Томаса

У_:     = ⁱ , / V e ^*' ^ ^m9*^v .

W      V2 i-V2)

вигнеровское вращение

.

(П2.25)

Тем самым отсюда следует, что величина угловой скорости (П2.24) форм-инвариантна

O' ^Y = a * ^Ya

* ²

i у v  eaivS *3*v +iea”a*XaaX =

V* (i - V*2)             2

ya i        ^"  apv QP Qv , i apy  uX ■ a- a --г-----г e v v +— e  a a

V ( i - V )          2

Следовательно, угловая скорость собственного вращения s′ в новой системе складывается согласно формуле (П2.25) из двух составляющих: новой собственной прецессии Томаса (первый член в левой части) и вигнеровского вращения (второй член в левой части), что и было отмечено в Примере 3. Таким образом, если жёсткая система отсчёта s′ движется таким образом, что в каждый момент лабораторного времени её координатные оси совпадают с осями мгновенно сопутствующей ей инер- циальной системой отсчёта ориентированной без поворота относительно лабораторной системы, то система s′ обладает собственной прецессией, которая и является прецессией Томаса. Собственное же вращение Вигнера дополнительно к прецессии Томаса, определяется матрицей вращения bβα и появляется при любом бусте. В том случае, когда система s′ в первоначальной лабораторной системе двигалась прямолинейно и равномерно ускоренно без собственного вращения, её собственная прецессия Томаса равна нулю. В новой лабораторной системе вращение Вигнера и прецессия Томаса системы s′ должны быть противоположно направлены и компенсировать друг друга. Их различие следует уже из определений (П2.12), (П2.25).

Таким образом, собственное вращение Вигнера и собственная прецессия Томаса представляют самостоятельные эффекты, тесно связанные между собой, но неэквивалентные понятия.