Remarks on first Zagreb indices

Let G = ( V, E ), V = { 1 , 2 , ...,n } , be undirected connected graph, where V = { 1 , 2 ,...,n } is set of vertices and E = { e ₁ , e ₂ , ...,e _m } set of edges. Further, denote with d ₁ >  d ₂ >  ... >  d _n , d i = d ( i ), i = 1 , 2 , ...,n , a sequence of vertex degrees of G . If e = { i, j } G E , then d ( e ) = d i + d j — 2. The first Zagreb index M ₁ and reformulated Zagreb index EM 1 are, respectively, defined by [8, 9]

M 1 = ^X d i ² and EM 1 = ^X d ( e i )² .

i =1                       i =1

If G is a graph and L ( G ) is a corresponding line graph, then the following equality is valid EM 1 ( G ) = M 1 ( L ( G )). Invariants M 1 and EM 1 play an important role in algebraic graph theory, as well as in other sciences especially in molecular chemistry (see [2, 5, 6, 8, 9, 12]). Since these invariants can be calculated for a few classes of graphs in a closed form, it is of interest to find out inequalities that determine upper and lower bounds of these invariants in terms of some graph parameters or their mutual relationship. This is the topic of this paper.

We first give two inequalities that establish a connection between M 1 and EM 1 proved in [5].

Theorem 1.1. Let G = (V, E), V = {1, 2,..., n}, be undirected connected graph n vertices and m edges. Then with

EM 1 > ( M i - ^2m) 2 ,

m with equality if and only if G is a regular graph.

Theorem 1.2. Let G = ( V, E ) , V = { 1 , 2 ,..., n } , be undirected connected graph with n vertices and m edges. Then

< ⁽ M 1 - ^2m) 2 ^(d 1 ⁺ d n - ^{2) 2}

EM ^{1 6}    4 m ( d — 1)( d „ — 1)    ’

where d n >  2 , with equality if and only if G is a regular graph or there are exactly m (+ n - 1) edges of degree 2( d 1 — 1) and dm + d n - ^ edges of degree 2( d _n — 1) such that ( d i + d n — 2) divides m ( d n - 1) .

• 2.    Main Result

The following theorem establishes a connection between invariants EM 1 and M i in terms of parameters m , d 1 and d n .

Theorem 2.1. Let G = ( V, E ) , V = { 1 , 2 ,..., n} , E = { e i , e ₂ ,..., e _m } , be an undirected connected graph. Then

( M ¹— 2 m - + 2( d 1 — d n ) ² 6 EM 1 6 ( M ¹— 2 m^ + 4 m ( d 1 — d _n ) ² a ( m ) ,      (3)

mm where

α ( m ) =

-

-

( — 1) ^{m +1}

2 m ²

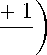
Equality holds if and only if L ( G ) is a regular graph.

C The following inequality was proved in [1] for positive real numbers p 1 ,p ₂ , ..., p _n , a i , a ₂ , ..., a n and b 1 ,b ₂ ,...,b _n with the properties 0 < r i 6 a i 6 R i <  + ro and 0 < r ₂ 6 b i 6 R ₂ <  + ^

nn    n   n

n

X P i — X P i J ,    (4)

i =i       i e S /

pi     pi ai bi -     pi ai     pi bi i=1 i=1          i=1     i=1

where S is a subset of In = {1, 2, . . . , n} for which the expression pi i∈S

-

n

2 X P i i =1

reaches a minimal value.

For n = m and S = {1, 2,... , k} C Im = {1, 2,... m} from (5) we obtain that k = b mm J. Now, for n = m, pi = 1, S = {1, 2,..., b mm J}, ai = bi = d(ei), i = 1, 2,..., m, Ri = R2 = 2(di — 1), r1 = r2 = 2(dn — 1) the inequality (4) becomes m          mm \ 2

^m XXX ^d( e i ^{) 2 —} (X ^d( e i )) ^{6 4(} d i ^— d n ^{) 2} [y] (m ^— [y] )•             ⁽⁶⁾

Since 522 =1 d ( e i ) = 52П =1 d 2 — 2 m = M 1 — 2 m , from (6) immediately follows right side of inequality (3).

Since the equality in (6) holds if and only if d ( e 1 ) = d ( e ₂ ) = ... = d ( e _m ), therefore equality on the right side of (3) holds if and only if L ( G ) is a regular graph.

For the real numbers a i , a 2 , . . . , a _m with the property r 6 a i 6 R , i = 1 , 2 , . . . , m , the following inequality was proved in [10] (see also [11])

m

^X i =i

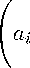
- m2

¹ X a i

m i=i

>

( R — r ) ²

For ai = d(ei), i = 1,2, ...,m, r = 2(dn — 1) and R = 2(d1 — 1) the above inequality transforms into m X i=1

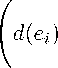
m ²

-- ^^ d ( e i ) j > 2( d i - d n ) ² , ^m i =1

i. e.

m            m ²

X d(ei)2 — £ Ed(e-)   > 2 d - d-)2- i=1                i=1

where from the left side of inequality (3) is obtained.

Equality in (7) holds if and only if d ( e 1 ) = d ( e 2 ) = . . . = d ( e _m ), so the equality in the left part of (3) holds if and only if L ( G ) is a regular graph. B

Remark 2.1. Since ( d i — d n ) ² > 0, left inequality in (3) is stronger than inequality (1).

Corollary 2.1. Let G = ( V, E ) , V = { 1 , 2 ,..., n } , E = { e 1 , e ₂ ,..., e m } be an undirected connected graph. Then

( M 1 — 2 m )( d 1 — d n ) 6 EM 1 6 -—¹------—+ m ( d 1 — d n ) ² .

mm

Equality on the right side holds if and only if L ( G ) is a regular graph. Equality on the left side holds if and only if G = K 2 .

C Inequality on the left side in (8) is obtained from the left side of inequality (3) and inequality between arithmetic and geometric mean for real numbers. The right side of inequality (8) is obtained from the right part of inequality (3) and inequality α ( m ) 6 ¹ ₄ . B

Corollary 2.2. Let G = ( V, E ) , V = { 1 , 2 ,..., n} , E = { e 1 , e ₂ ,..., e m } be an undirected connected graph. Then

4 m ( d _n — 1) 2 + 2( d 1 — d n ) ² 6 EM 1 6 4 m ( d 1 — 1) 2 + 4 m ( d 1 — d _n ) ² a ( m ) .        (9)

Equalities hold if and only if G is a regular graph.

C Inequalities (9) are obtained according to the inequality (3) and inequality

2 m ( d _n — 1) 6 M 1 — 2 m 6 2 m ( d 1 — 1) . B

Corollary 2.3. Let G = ( V, E ) , V = { 1 , 2 ,..., n } , E = { e 1 , e ₂ ,..., e m } , be an undirected connected graph. Then

) + 2( d 1 — d n ) ² 6 EM 1 6 -— m   (2 m + ( n — 1)( n — 4)) ² + 4 m ( d 1 — d _n ) a ( m ) .

( n — 1) ²

4 m

2 m n

Equality on the left side holds if and only if G is a regular graph. Equality on the right side holds if and only if G is a complete graph, i. e. G = K _n .

C The result immediately follows from inequality (3) and inequalities M 1 >  ^{4 m} _n ² , proved in [7], and M 1 6 m ( nm l + ( n — 2)), proved in [4]. B

Theorem 2.2. Let G = ( V, E ) , V = { 1 , 2 ,...,n } , E = { e 1 , e ₂ ,..., e m } , be an undirected connected graph. Then

EM 1 6 ( M i — 2 m )( d 1 + d n — 2) — 4 m ( d 1 — 1)( d _n — 1) .               (10)

Equality holds if and only if G is a regular graph or a graph with the property that for some k , 1 6 k 6 n , sequence of vertex degrees is of the form d ₁ = d ₂ = ... = d k > d k +i = ^d k +2 — • • • — ^d n -

C For the real numbers a i , a 2 , • • •, a m with the property r 6 a i 6 R , i — 1 , 2 ,..., m , the following inequality was proved in [3] (see also [11])

m

1X

m i=1

a i

-

m ²

^{1 X} a i

m i=1   /

m

R-m   ai i=i

m

1 Xai m i=i

- r

For ai — d(ei), i — 1, 2,..., m, r — 2(dn — 1) and R — 2(d1 — 1) the above inequality becomes mm m1       d(ei) - m1     d(ei)

i =i                i =i

m

2( d i — 1) — m X d ( e i ) i =i

m

¹      d ( e i ) - 2( d n

m i=i

-

)

i. e.

1 ^m

X d(ei)2 6 2(di + dn m i=i

m

^{— 2)} ^^ ^{d (} e i ) ^{— 4(d} 1 ^{— 1)(d} n ^— 1) , i =i

where from the assertion of the theorem is obtained. B

Remark 2.2. According to (10) the following inequality is valid

EM ₁ + 4 m ( d ₁ — 1)( d _n — 1) 6 2( M ₁ — 2 m )( d ₁ + d n — 2) .              (11)

Based on the inequality between arithmetic and geometric means for real numbers and applying it on the left part of inequality (11), the inequality

2P4m(d1 — 1)(dn — 1)EM 6 2(M — 2m)(d1 + dn — 2), dn > 1, is obtained, i. e.

< ⁽ M 1 — ^2m) 2 ⁽ d 1 ⁺ dn¹ — ^{2) 2}

.

EM 1 6 ------—--- ttt7 ---77---

4 m ( d 1 — 1)( d n — 1)

This means that inequality (10) is stronger than inequality (2).