Research of IGPC Control Strategy Based-on Hybrid Optimization for Power Station Boiler Superheated Steam Temperature

Published Online January 2014 in MECS

• I.    Introduction

2.1 GPC Law Computation

As a new type of predictive control method, GPC has better performance for its collection of the merits of multiple algorithms, and forms a variety of improved predictive control algorithm in the actual use[1][2][3]. But traditional GPC assumes that the controlled processes are both linear and unconstrained, and uses gradient optimization method to obtain optimal predictive control increment based-on the minimization of error between system output and expected value, and the minimization of the quadratic form objective function with control incremental weighted term. But in practical industrial process, completely unconstrained control system is rare, most systems have various constraint conditions, such as the saturation constraint on the control action and its change rate, as well as the constraint of system output, etc. In considering these constraints, the constraint quadratic programming should be solved, also objective function and constraint condition must be differentiable, and commonly only locally optimal solution is obtained. To improve GPC performance and extend its application, the effective method to solve the optimization problem must be researched[4][5][6]. The paper proposes IGPC based-on PSO hybrid optimization, this modified IGPC can be applied to both of the constraint and non-constraint industry process control.

Superheated steam temperature of high temperature superheater for power station boiler is one of the main control parameters in power plant thermal control system. Under serious interference and varied working condition, ideal control effect is difficult to achieve with the common used conventional cascade PID control, therefore, many of the new predictive control method with the combination of traditional PID control strategy are obtained[7][8][9][10].

The main research contents of the paper include the following three aspects. Firstly, aiming at the controlled object described with CARIMA model, GPC law equation is derived, in order to avoid the direct solution of the Diophantine equation, the paper further derives the calculation process of IGPC algorithm, IGPC algorithm adopts the direct identification of controller parameters without the need to solve the controller parameters by online recursive solution, so it can reduce the online computation time. Secondly, PSO algorithm is introduced into the GPC rolling horizon optimization, a practical hybrid optimization strategy is obtained, so the strategy may improve the searching speed and precision, and thus improve IGPC performance. Lastly, aiming at the superheated steam temperature control system of Power Station Boiler, a new cascade compound control strategy that combines an outer loop IGPC master adjuster with PSO and an inner loop PID auxiliary adjuster is adopted, the effective simulation results are obtained under some constraint conditions.

II. IGPC Algorithm

Suppose the mathematical model of the controlled object is described by the following CARIMA model[6]:

A( z-1) y ( k ) = B (z — )u (k — d ) + C (z-* )£( k ) / A

A (z-1) = 1 + a1 z-1 + ■■■ + anaz "na

Where: B(z4) = b0 + bz"1 + • • • + bnbz"nb

C (z-1) = c 0 + c z-1 + ••• + CnCz - nc

A = 1 _{— z} ^— is the differential factor, y ( k ), u ( k ) are the output and input of system, ^ (k ) is the zero-mean random noise sequence.

For the above formula, the easy mathematical treatment ( d =1) is used, and both sides are multiplied by the difference operator △ , thus we can obtain the equation as follows:

A ( z ■') y ( k ) = B ( z ■' ) A u ( k — 1) + C ( z — )« k )     (1)

Where: A ( z "*) = A ( z "*)A

Introducing the following Diophantine equation:

T ( z -¹) y ( k + j )

= Gj ( z -¹ ) A u ( k + j — 1) + Ej ( z -¹ ) A u ( k — 1)

+ S j ( z -¹) y ( k ) + R j ( z -¹) C ( z -¹ ) £ ( k + j )

y ⁽ k + j )

= Gj . ( z "1 )A u^ ( k + j — 1) + Ej . ( z ') A u_$ ( k — 1)

+ S j . ( z -¹) y_f ( k ) + R ( z -¹)( C (— ) £ ( k + j ) T ( z )

= Gj ( z ⁴ )A u_f ( k + j — 1) + Ej ( z ^{— 1} )A u_f ( k — 1)

+ S ( z -¹ ) y_f ( k ) + R -( z -*) ^ ( k + j )

Where:

' y_f ( k ) = y ( k )/ T ( z -¹)

< _{M /} ( k ) = u ( k )/ T ( z "')

П ( k + j ) = C ( z -*) ^ ( k + j )/ T ( z -¹)

When j increases from 1 to P , the matrix form of Formula (3) can be written as follows:

У ( k + 1) = G A Uj ( k ) + E ( z "1 ) A u_$ ( k — 1) + S ( z -¹) y_$ ( k ) + R ( z "^x)n< k + 1)

Where:

У ( k +1) = [ y ( k +1), y ( k + 2),..., y ( k + P ) ] T

A U _f ( k ) = [A u _z ( k ), A uj ( k +1),..., A u _z ( k + P — 1)] ^T n ( k +1) = [ n ( k +1), n ( k + 2),..., n ( k + P )] ^T

E ( z -¹) = [ E , ( z Л E 2 ( z -¹ ),..., E p ( z -> )] ^T

S ( z -¹ ) = [ S 1 ( z -* ), S 2 ( z -¹),..., S p ( z -‘)] ^T

_ R ( z -¹) = [ R 1 ( z -¹ ), R 2 ( z -¹),..., R p ( z -*)] ^T

g 0      0    0   0

g ₁ g ₀00

T (z-1) = Rj (z-1) A( z-1) + z "jSj( z-1)(2)

Where: T ( z ') is the filter polynomial, generally using the first order filter.

—1

Rj (z-1) = 1 + 5 j"j , Sj (z’ ) = 5 siz"i i=1

Take: Gj (z"1) = G,. (z"1) + z"jE,. (z"1)Where: Gj (z-1) = B(z-1)Ry.(z—)

deg G j = П ь + j — 1;deg G j = j — 1;deg E j = n , — 1

Then formula (1) can be changed into:

gp—1   gp — 2   • ••  g 0 J P x P

Introducing the rolling horizon optimization

performance index:

P

J = E <5 [ y (k + j) — yr (k + j )]2

< j = 1

p

+ 52j[Auf (k + j — 1)]2 > j=1

Where: P is the maximum length of prediction horizon, Xj is the control increment weighting coefficient, y_r ( k + j ) is the input reference trajectory. Formula (5) can be expressed in the following matrix form:

J = E { [ У ( k + 1) - Y r ( k + 1)] ^T [ Y ( k + 1) - Y_r ( k + 1)]

+ [ A U T ( k ) 2 A U_f ( k )] }

With the assumptions:

E { [ R ( z ^{- 1} ) n ( k + 1)] ^T AU, ( k ) } = 0, E { R ( z"^VMk + 1) } = 0 , by using the derivation to a U_f ( k ), formula (6) can be simplified into the following control law equation:

• - E ( z -¹) A u^ ( k - 1) - 5 ( z -¹) y_f ( k )]

For the above formula, taking the first line, the realtime control increment is obtained as follows:

• f                r                           f               ₍₇₎

• - 5 ( z -¹) y_f ( k )]

• 2.2 IGPC Algorithm Computation

Where: d ^T = [1  0       0] ( g^tG + 2 I )^- ' G ^T

To solve the optimal control law by using the above algorithm, the online recursive calculation of Diophantine equation is required. For the controller parameters must be solved beforehand, then can the control law be solved, this heavy calculation leads to big CPU resources consumption in real-time industrial control. Here an implicit algorithm is adopted [11][12][13], it can directly identify controller parameters without the need to solve the Diophantine equation, so it can save the online computation time.

The formula (4) is expanded as follows:

У (k +1) = g 0A uf (k) + E1( z "1)A uf ( k -1)

+ 5 1 ( z -¹) y f ( k ) + R^ z "*) n ( k + 1)

У (k + 2) = g 1A Uf (k ) + g 0A uf (k + 1)

+ E ₂ ( z "*) A u f ( k - 1)                     ₍8)

’           + 5 2 ( z -¹) y f ( k ) + R ₂ ( z -*) 7 ( k + 2)

y (k + P) = gp-1A uf (k) + ■ • • + g 0 A uf (k + P -1)

+ E p ( z "*) A u f ( k - 1) + S p ( z "*) y f ( k ) + R p ( z "*) n ( k + P )

In order to identify G, the P equations in the formula (8) are identified, but the amount of calculation is large, so this scheme is not desirable. It can be noted from formula (8), all of the elements g0, gx ,..., gp_x in G matrix appear in the last line of formula (8), all elements of matrix G can be obtained only through the identification of the last line prediction, at the same time, Ep (z ') , Sp (z ') can also be identified. Thus following formula can be obtained:

f ( k + P ) = E p ( z -¹) A u f ( k - 1) + S p ( z -¹) y f ( k )

In this way, a least squares identification is only needed.

Take the last line of formula (8):

y ( k + P ) = g_{p - 1} A u_f ( k ) + g_p _ ₂ A u_f ( k + 1) + • • •

• + g 0 A u f ( k + P - 1) + E p ( z -¹) u f ( k - 1)   (9)

• + 5_P ( z -¹ ) y f ( k ) + R_P ( z -¹ ) n ( k + P )

= ф ( k )) в + R_P ( z "*) 7 ( k + P )

Where:

ф ( k ) = [ A u _y ( k + P - 1), • • •, A u, ■ ( k ), A u, ■ ( k - 1), , ^{A u}f ⁽ k ^- n b \ y_f ⁽ k X--', y f ⁽ k ^- n a ^{)] T}

6   [g0,“ *, gp-1, ep,0,“ *, e

T

,    P ,0 ,     ,    P , n_a ]

Predictive control has a characteristic, A u ( k ) , A u ( k + 1) ,^, A u ( k + P - 1) can be obtained at the moment of k , in that way ф ( k ) is decided by the current and past observations { y ( k ), u ( k ) } of the system. When C ( z ') = T ( z ') , the noise term R_p ( z ^-1) n ( k + P ) of formula (9) on the right contains the random disturbance of the system in the future time, so it is orthogonal to the ф ( k )6 , here, the obtained output predicted value is the optimal prediction.

or: y_p ( k / k - P ) = ф ( k - P) 6

Therefore, the identification equation is:

y ( k ) = ф ( k - P )6 + ^ ( k )                  (10)

By using formula (10), ^^₀ , ^^₁ ,^, ^J _{p - 1} and jEp ( z '), Sip ( z ^-1) can be identified, so f ( k + P ) can be obtained, that is the following formula:

f ( k + P ) = E r p ( z-^x) A M_f ( k - 1) + 5 p ( z -¹) y f ( ^k )

The next step is how to solve:

f ( k + i ) = E i ( z "-) A u f ( k - 1) + 5 , ( z -¹) y f ( k ) ( i = 1,2,---, P - 1)

Rewrite the first P -1 lines of formula (8):

• + тФ R i (*"¹' ^ ^<-k + * )

So the output predictive value is obtained as follows:

+ £ gi Auf(k - j + i- 1)       (11)

^j = 0

From the control law formula (7), a set of control law A u_f ( k ) ,..., A u^ ( k + P - 2) can be obtained at the moment of k -1, so A u_f ( k + i - 1)( г = 1,2,---, P - 1) is known at the moment k . At the same time, the predictive value y_p (( k + P )/ k ) = ф ( k) 0 of step P can be obtained at the every moment k , as a result, y_p ( k + i / k ) , (i = 1,2,-••, P - 1) can be obtained by calculation at the moment k + i - P (Assuming that the estimated parameters in step P remain unchanged):

Ур ((k + i) / k) = Ур ((k + i) / (k + i - P)) =ф (k+i - p )e(i = 1,..., p -1)

Thus, f ( k + i ) can be directly calculated by formula (11), the all parameters of controller can be obtained without identification.

f (k + i) = Ур ((k + i)/ k)

• - £ g ? j A U f ( k - j + i - 1)       (12)

j = 0

(i=1,..., P -1)

In summary, IGPC algorithm can be summarized as follows:

Step 1: set the initial value of parameters;

Step ² : identify gr 0, g_v...,д^ р _ 1 and E-_р ( z ^-1 ), Si _P ( z ^by formula (10), compute I?_p ( z"’ ) A u_f ( k - 1) + Sip ( z "') y_f ( k );

Step 3: solve f ( k + i ),( i = 1,2,-••, P - 1) by formula (12);

Step 4: compute the control law by formula (7);

Step 5: return to Step 2.

IGPC algorithm adopts the direct identification of controller parameters. It does not need to solve the controller parameters by online recursive solution.

• III.    Hybrid Optimization Strategy based-on PSO Algorithm

• 3.1    Fundamental Principle

PSO algorithm adopts velocity-displacement model, so it is easy to understand, easy to realize, does not require differentiable object function and constraint condition, it can quickly obtain the globally optimal solution with larger probability, currently this algorithm has obtained successfully application in many optimization problems[14][15]. According to the following formula, particle speed and position are updated.

x_i = x_i + v_i

Where: v is particle velocity, c , c is learning factor. rand() is random number between [0,1], x is particle current position, p and g are the current extreme value of particle and particle swarm. ω is influencing factor that the last speed influences the current flight speed.

PSO algorithm was introduced into the GPC rolling horizon optimization, thus a new hybrid optimization method combined with general GPC gradient optimization method under unconstrained condition is obtained. In the controlled object without constraints, gradient optimization is used to obtain the optimal control input. Under the constraint, gradient optimization will cooperate with PSO algorithm, thus the optimal control input is obtained fast and accurately. GPC structure based-on PSO hybrid optimization algorithm is shown in Fig. 1.

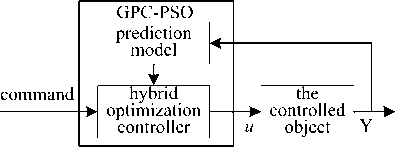
Fig. 1: Control structure based-on PSO hybrid optimization

• 3.2    Hybrid Optimization Strategy

• 3.2.1    Parameter Setting Strategy of Constrainted PSO Algorithm

Particle swarm algorithm is a random search and solving algorithm, a disadvantage is that the computation time is often longer, and may even fall into the local optimum. Therefore, the conventional particle swarm algorithm is difficult to apply directly to the real time industry process control, in order to overcome the limitations of the particle swarm algorithm, the paper adopts the following several strategies to improve the search speed and accuracy of particle swarm algorithm in the use of particle swarm algorithm for the optimization of GPC, finally good performance of realtime control is obtained.

In order to quickly and accurately obtain optimal value, PSO algorithm will depend on the fitness function selection and the population initialization and the weight ω setting strategy etc. Following some modified strategies for PSO algorithm are introduced in the initial parameters setting[16].

• (1)    Fitness function

When GPC is used to optimize, the system output is hoped as close as possible to the given value. In order to make the control increment A U accord with the actual production, don't want it to have great change. So, formula (5) is adopted as the fitness function of PSO algorithm, its optimization target values is 0, the minimum error criterion is 0.01.

• (2)    Population initialization

In general PSO algorithm, population initialization is random, and the speed of convergence is relatively slow. In reality, the optimal solution o f a large class of constrained optimization problems is in the constrained boundary. Accordingly, the paper by using the gradient optimizing in the case of unconstrained condition will get the optimal solution sequence A U through the minimization of the two type objective function in the particle swarm initialization process, and introducing the constraint condition, the elements of the sequence beyond the constraint conditions are set with the end boundary value, then the A U as the initial value is assigned to θ% seed in the population, the remaining seeds are randomly assigned to the initial value, here seed dimension is control time domain m. By this method, the population contains a part of high quality seed, as well as ensures the diversity and randomicity of population, thus it can accelerate the algorithm convergence speed, reduce the computation time, and avoid the local minima to a certain extent.

• (3)    Weight ω Setting

Shi[14] researched effects of inertia weight ω on the optimal performance, found that large ω value is advantageous to jump out of local minima and has the strong global search ability, but smaller ω value is advantageous to algorithm convergence. Therefore, in the setting of ω, the initial value ω is set to 0.7, also its value is linearly reduced to 0.2 with the increase of the number of iterations.

• (4)    Iteration Termination Condition Setting

When iteration termination condition of a general PSO algorithm is to reach the maximum number of iterations or meet the minimum error criterion, the iteration is stopped. Because of the existence of constraints in many cases, the optimization goal of GPC in the case with constraints is difficult to achieve 0, as a result PSO algorithm has obtained an optimal value, but the optimization will continue to search until the algorithm reaches a maximum number of iterations and then terminates the iteration, a lot of time is wasted. Thus we can introduce the two parameters of a stable accuracy δ and maximum stable continuous iteration number b in the particle swarm algorithm, this parameters are used to judge whether the algorithm has obtained an optimal value, and then decide whether to terminate the iteration. This can save a lot of time and improve the real-time performance of PSO algorithm. Specific process is as follows:

IF (The current fitness of the optimal particle － The last time fitness of the optimal particle)<δ

Then flag=flag+1

ELSE flag=0

END IF

IF (reach the maximum number of iterations) OR (meet the minimum error criterion) OR (flag=b)

Then (terminate the iteration, give the optimal solution)

END IF

• 3.2.2    Soft Switching Strategy

• 3.3    The Algorithm Flow based-on PSO Hybrid Optimization

This important strategy is to ensure real-time GPC-PSO system. When the system is in steady state, fluctuation is lesser for optimal predictive control input increment, here optimal control increment obtained by unconstrained GPC basically can satisfy the constraints. Considered from the aspect of real-time, it may directly use unconstrained GPC to obtain the optimal control increment in order to save the running time of algorithm, it does not need to call the PSO algorithm. Therefore, a soft switch is arranged in the controller to switch. Specific methods are as follows:

IF the optimal input control increment sequence A U meets the constraint conditions of the controlled object according to the two type objective function of the unconstrained GPC

Then directly use u(k-1)+ A u(k) as a control variable to control the system

Else start the PSO algorithm for solving constrained optimization, then act on the system with this optimal control input

END IF

The GPC algorithm flow based-on PSO hybrid optimization is shown in Fig. 2.

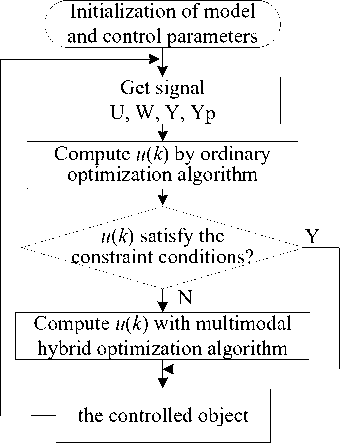
Fig. 2: Software flow chart of hybrid optimization GPC algorithm

• 3.4    Algorithm Simulation

The simulation research is implemented based-on the model provided by reference [4] in various constraint conditions:

A (z ^{- 1})=1 - 0.4z ^{- 1} - 0.32z ^{- 2},

B (z ^{- 1})=0.1, C (z ^{- 1})=1

Constraint condition:

- 10 ≤ u ( k ) ≤ 10, - 5 ≤ u ( k ) - u ( k - 1) ≤ 5, - 2.55 ≤ y ( k ) ≤ 2.55 , ξ ( k ) is [-0.1, 0.1] uniformly distributed white noise.

Simulation parameter settings: The population number of PSO is 20, Maximum number of iterations is 100, Learning factor c = c = 2 , Stable precision δ =0.001, Maximum continuous stable iteration number b =5, High quality seed ratio 0%=2O%. The simulation results are shown in Fig. 3.

From the simulation results, the hybrid optimization method is feasible and has good control effect for the controlled object with many kinds of constraint condition.

Cl 50      100     150     200     250     300     350400

0      50     100     150    200    250    300    350400

t

0      50     100    150    200    250    300    350400

Fig. 3: Algorithm simulation result with a variety of constraints

• IV.    Superheated Steam Temperature Control for Power Station Boiler

• 4.1    Cascade Control System based-on IGPC and PID

• 4.2    Simulation Study

The main steam temperature control of power station boiler is one of the important parameters of the unit safety and economic operation. Common control methods include the double loop control system of conventional cascade PID controller or differential compensation signal, but because of the characteristics of steam temperature controlled object with large delay and large inertia, these control methods are difficult to obtain the optimal control effect. The actual situation shows that, although many power plants have used Distributed Control System (DCS), but the control quality of steam temperature is still not ideal, steam temperature will deviate from the set value above 8C even when the load changes with only 2%MCR/min rate for some power plants, so often the main steam temperature can only be controlled by manual operation, also the stable range is expanded to the scope of ±6 °C, this will reduce the economic operation of the unit and increase the labor intensity of operator.

Superheated steam temperature control scheme in the paper adopts the cascade control system which combined IGPC with PID, it don't change the inner loop characteristics of the traditional cascade PID control system, only use IGPC instead of the outer loop master adjuster. Combined the inner loop PID controller with the superheated steam temperature object, the generalized controlled object model is as shown in Fig.4.

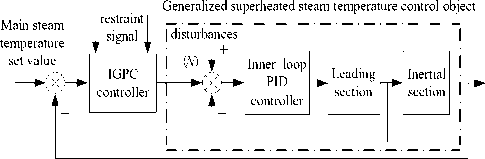
Fig. 4: Schematic diagram of superheated steam temperature control system based-on IGPC

The paper will do simulation studies based-on previous modeling results of boiler superheated steam temperature system in a Anhui power plant #2 boiler (600MW subcritical boiler)[13], and choose A side primary desuperheater, forward screen, backward screen model as an example. The transfer function of primary desuperheater is 0.270     - 15 5 , The transfer

(1 + 26.195) e function of forward screen A is_______0.482_______ -37s,

(1 + 27.74 5 )(1 + 28.65 5 ) e

The transfer function of backward screen A is

0.576     - 46 5 . Inner PID algorithm parameter Kp is

(1 + 155.59 5 ) e

• 50,    thus comprehensive main loop model is ___________________ 3.75 ___________________ ^-98 ⁵ . The paper (1 + 26.19 5 )(1 + 27.74 5 )(1 + 28.65 5 )(1 + 155.59 5 ) e

will use this superheated steam temperature model as the simulation research object.

Simulation parameter settings: The population number of PSO is 20, Maximum number of iterations is 100, Learning factor c_t = c₂ = 2 , Stable precision δ =0.001, Maximum continuous stable iteration number b =10, High quality seed ratio 6 % = 20 % . The simulation results are shown in Fig.5.

Where, A u is limited in [-5,5], The valve opening is limited in [0,100], the down load disturbance on the system is done in 100th minutes, from the simulation figure we can see, the output temperature of the system will be back to the set temperature of about 540 °C after deviation from the set value of 4C.

From Fig. 5, IGPC has a strong constraint function on the control action, thus it is able to control the input in the scope of constraint, so effectively prevent the dramatic changes in the input signal. At the same time, the system has good control performance, and meets the requirements of actual control. IGPC algorithm has good robustness for the order number and parameters changes of the model, and can adapt to control power station boiler superheated steam temperature.

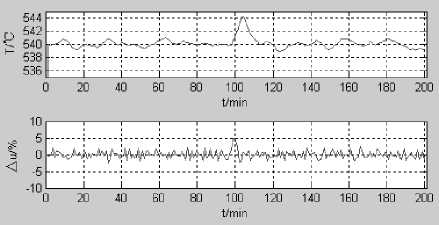
Fig. 5: Simulation curve of the main stream temperature control

• V.    Conclusion

Combined PSO algorithm with unconstrained GPC gradient optimization method, a new hybrid optimization algorithm is obtained, it may improve optimizing rate and precision, this method not only can obtain good control effect for unconstrained controlled object, but also obtain good control effect in case of multiple constraints through the simulation research. This improved IGPC will help promoting GPC application in more industrial process control.