Research of Self-Tuning PID for PMSM Vector Control based on Improved KMTOA

Published Online March 2017 in MECS

Due to PMSM offers certain advantages such as small volume, high efficiency, low moment of inertia, large electromagnetic torque and so on, permanent magnetic synchronous motor drive systems are also widely employed in precise positioning of end effectors in robotic applications, electric and hybrid electric vehicles etc.[1-2]. During the actual operation, the variation of the load torque and speed of PMSM will have a bad effect on the high precision control system [3].

The PMSM is a nonlinear control system and strong coupling among the rotor speed and the winding currents [3]. Nowadays, many methods of nonlinear control algorithms have been proposed in order to enhance the control performance of PMSM. Owing to small steadystate error and easy implementation, the proportionalintegral-derivative (PID) are the most widely adopted controller in the industrial PMSM drives. The PID controller included a whole set of controller parameters aims to provide an optimal behavior in terms of the response to a speed command, a load disturbance, and parametric uncertainties [4-5]. Generally, many optimization algorithms of PID parameters was proposed by the researcher, such as Z-N algorithm, ant colony algorithm, particle swarm optimization algorithm (PSO), genetic optimization algorithm, fuzzy RBF neural network adaptive control and so on [6-10]. However, these control strategies are flawed, such as control is more complex, difficult, poor robustness and so on.

In the parameter setting of the PID controller for accurate speed control in PMSM drives. A improved kinetic molecular theory optimization algorithm is proposed in this paper. The algorithm made use of the advantage of randomness and ergodicity of chaotic system. In modified algorithm, an inertia weight was adjusted adaptively with nonlinear strategy, and chaotic searching is conducted within the neighbour set of the solutions to avoid the local minima. The simulation platform MATLAB/Simulink is used to set up the model of PMSM and its space vector control system. The result of the simulation will be compared with the conventional PID and particle swarm optimization algorithm to verify the effectiveness of the proposed methods.

This paper is organized as follows. Section 2 describes mathematical model of PMSM. The principle of PMSM vector control system is provided in section 3. A brief introduction to the KMTOA algorithm and improved KMTOA algorithm, also the improved KMTOA algorithm has been applied for self-tuning of PID controller is proposed in section 4. In section 5, the selftuning CKMTOA PID controller has been applied for the PMSM vector control system and result analysis are shown. Section 6 is conclusions of this paper.

• II.    Mathematical Model of PMSM

In the d-q synchronously rotating reference frame, the mathematical model of PMSM is much simpler than the static reference frame of three-phase A-B-C and a-p-o . The d-q synchronously rotating reference frame makes the variable coefficient differential equations of the motor convert to constant coefficient equation and eliminates the time-varying coefficient which simplifies operation and systematic analysis. It is benefit for operating the control system. Then the mathematical model of surface mounted permanent magnet synchronous motor in the d-q synchronously rotating reference frame can be expressed as following equations.

To establish the PMSM healthy model, without loss of generality, the assumptions are as follows. Firstly, the magnetic circuit is not saturation. Secondly, the eddy currents and the hysteresis losses are negligible. Thirdly, the electrical conductivity of the permanent magnetic material is zero. Fourthly, the rotor magneto motive force is sinusoidal and the slot effect is neglected. Lastly, the stator winding current is sinusoidal, symmetrical and non-harmonic.

The stator voltage equation of PMSM in the d-q synchronously rotating reference frame are as follows:

axis’ inductances, R Ω is the damping coefficient, n p is number of pole pairs by motor, ^ is rotor flux linkage, J is moment of inertia, T is load torque.

The model of surface PMSM given by (1), (2) and (3) is written in state space form equation as follows:

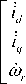
R S —

L

- n p ^ r

n p ^ r

R s

—

L

1.5 n p V f

J

n p V f

L

B

J

ud

L

d

*

+

u q

.

^

L

—

T L

J

Where B is viscous friction coefficient by motor.

L^ = L = L is stator inductance for surface PMSM. dq

di ud = Rsid + Ld-^ — n.^rL'q di uq = Rsiq + Lq-^ + np^Ldid + np^Vf

The electromagnetic torque equation is written as:

Te = 2 np [Vf iq + (Ld — Lq )idiq ] •

The moment balance equation is written as:

T -T = Jd^r- + R ^.(3)

e    l^ dt

Where i d and i q are the d-q axis’ currents, u d and u q are the d-q axis’ stator voltages, R s is the stator resistance, ω r is Rotor mechanical angular speed, L d and L q are the d-q

III. Principle of Pmsm Vector Control

Vector control allows the control the speed, position and torque of the PMSM based on its d-q model described previously. The two closed control loops are generally implemented by PI controllers with fixed parameters because its structure is simple and well known [14]. The outer loop is the speed closed loop and the inner loop is the current closed loop. The desired d-axis stator current reference ( i d^* ) is set to zero to operate with maximum efficiency. Five modules are included in this control system and they are PMSM module, the information collection module, 3-phase inverter module, coordinate transformation module and SVPWM module. The speed deviation of the motor actual speed V and the reference speed V ^* is processed by ASR controller will produce the reference q-axis current loop command i q^* . Then the reference current i q^* and the motor actual current i q deviation is processed by PI controller will output u q . The setting i d^* =0 and the motor actual current i d

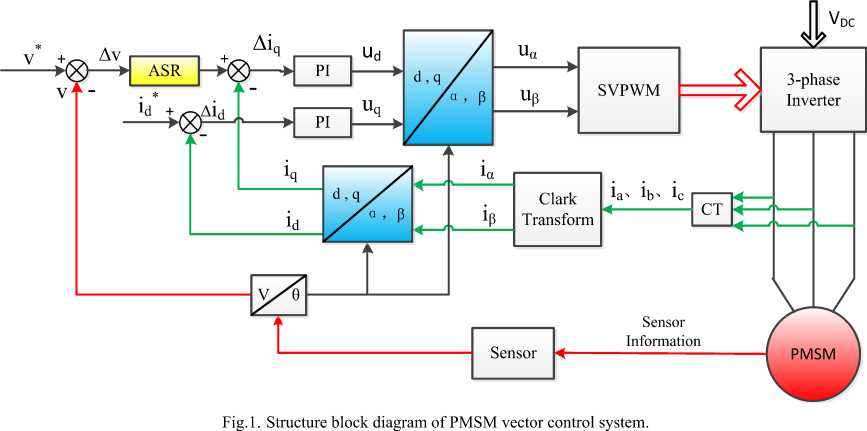
deviation is processed by PI controller will output u d . The d-q axis’ stator voltages u q and u d are processed by the iPark coordinate transformation will output u and u , which as the control signal of SVPWM. Then the SVPWM control signals will control the three phase voltage inverter to drive PMSM.

Fig.1 shows a typical structure block diagram of PMSM vector control system with two closed-loops control. However, they can’t give enough precision for electric and hybrid electric vehicles because the dynamic behavior depends on the operation mode and its parameters changes in time.

• IV.    The Self-Tuning Ckmtoa PID Controller Design

• A.    Kinetic-molecular theory optimization algorithm (KMTOA)

KMTOA is a new type of optimization algorithm be generated through simulate physical laws [15]. KMTOA is proposed by Chao-dong FAN in 2013 and the algorithm has been continuously improved in the past two years. The basic content of kinetic-molecular theory are as follow. The main content of KMTOA includes attraction, repulsion and thermal motion. The molecule is attraction if rand <  p_x ( rand is a uniform random variable in the interval [0, 1]). The attraction equations can be express as follows:

F i = GM i M best ( к .  , - X )          (5)

Where F is the attraction exerting on individual X ; G is a gravitational constant; M and M are the masses related to the individual X and optimal individual Xb_es, ; P 1 , p 2 and p 3 ⁽ p ^ + p 2 + p 3 =1 ) respectively represents the probability of this individual attracted, repulsion and thermal motion by the optimal individual.

The repulsion equations can be express as follows:

If p_x <  rand <  p_x + p₂

F_t = — GM i M best ( X    — X i ).

By the laws of motion, the acceleration of the individual X can be express as follows:

a

F i

M i

The resultants of the individuals which are at the balance position are zero and it is not helpful for optimization. Therefore, these individuals could simulate the thermal movement and increase population diversity to the effect of optimization. The condition that the resultant of individual x is zero is: ( p_x + p ₂) <  rand < 1.

These individuals could do irregular thermal movement. The acceleration of the individual X can be express as follows:

If rand < pc a-j = AX     Xmj N (0,1)        (8)

Where aij is the j-th component of individual X ; p e [0,1) is the mutation rate ; X and X are the pc      ,                                         max, j           min, j upper and lower bounds of the j-th components of solution space; A represents the amplitude expressed by following formula: A = 1 — 0.9t / T (t is the current number of iterations and T is the total number of iterations); N(0,1) is a normally distributed stochastic variable.

The velocity and position can be express as follows:

V = ® V ( t ) + a ,..                  (9)

X - ( t +1)= x, ( t )+ V , ( t ) .              (10)

Where ω is inertia weight.

The elitism strategy can avoid losing the optimal individual. Elitism strategy are as follows. Assume Хц™а = Х is the optimal individual at generation t-th, that J (Хв.а. (t)) = min( J (Xj (t)) , j e{1,2, ■■■, S} (S represents the population size, J(X   (t)) is represents the objective function value of X(t)). At the next iteration, if J(ХВея(t + 1))>min( J(X; (t +1)) , it means that the optimal individual degenerates. Meanwhile, let Х, = Хва..

• B.     Improved chaotic Kinetic-molecular theory

optimization algorithm

The KMTOA relies on the current optimal molecules in the population for optimal operation. It is easy to cause the error convergence of the algorithm when the optimal value is a local extremum. In this paper, the chaos theory is applied to the kinetic molecular theory optimization algorithm. The chaos theory studies the systems that follow deterministic law but exhibit random and unpredictable behavior [16]. Due to these characteristics, chaos theory is applied in optimization. It is advantageous to jump out of the local optimal and fast search to the optimal solution, and improve the accuracy of the solution. In this paper, the successions are made by the logistic mapping instead of above mentioned random numbers. Sequences generated by the logistic mapping are formulated as below:

Z jk + 1 = p z j, _k (1 — Z j , _k ), k = 0,1,2...,  0 <  Z j0 <  1.   (11)

Where z j _,k is a real-valued sequence and μ is the control parameter    (here,      μ=4 ,     z₀ ∉{0,0.25,0.5,0.75}).

Subsequently, the logistic mapping begins to enter a chaotic state.

The chaotic theory is introduced into the iterative process of kinetic molecular theory optimization algorithm. The current part of the better molecular position is used to produce a chaotic sequence.

X j + k = x * j + z_b k , k = 0,1,2,.... (12)

Where x j^* is current part of the better molecular position. Then, the previous particle is replaced by that sequence.

Generally, electric car and hybrid electric vehicles needs the PID parameters be tuned at the appropriate value quickly during startup. Then make fine adjustments according to the load torque to improve the performance of the system. From the formula (9) shows that the value of the inertia weight ω has an important impact on the convergence of the algorithm. So we use adaptive inertia weight factors in the speed updating and the equation can be express as follows.

dependent on the object of the mathematical model, there are relatively good adaptability and strong robustness. A mathematical description of the PID controller as:

u ( t ) = K  e ( t ) + K.0e ( t ) dT + К;^ИЛ .

p                           dt

to = <

to min

( to   - to )( f - f )

max     min         min

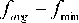
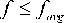
to max

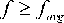
Where e ( t ) = r ( t ) - y ( t ) is the error signal, r ( t ) is the reference input signal, y ( t ) is the output signal.

Due to the conventional PID can not to meet the high precision control requirements when the variation of the load torque and speed of PMSM. The problem is the precise and optimal tuning of PID coefficients. Therefore, this paper research realization design of chaotic kinetic molecular theory optimization algorithm (CKMTOA) technique for tuning the PID speed controller adaptively.

The well-known fitness function value include Integral Absolute Error (IAE), Integral Time Squared Error (ITSE), and Integral Time Absolute Error (ITAE). In this paper, the ITAE is chose as the fitness function value. The ITAE equation as follows:

to

J = . t|e(t) | dt .

Where to and to is maximum and minimum inertia min max weight respectively, f is the current fitness function value, favg is the current fitness function value of the average of all particles, fmin is the minimum fitness function value.

The improved chaotic kinetic-molecular theory optimization algorithm of the following steps.

Step 1: Initialization of the positions and velocities of the population.

Step 2: Calculate the fitness of each individual and the selection of the best position X .

Step 3: Determine that the resultant force of each molecule is attraction, repulsion or zero. Calculate the resultant force between the molecule and the current optimal molecule by (5) or (6). And calculate its acceleration by (7) or (8).

Step 4: Update each molecule’s velocity by (9), and its position by (10). Update ω of adaptive inertia weight factors by (13).

Step 5: Calculate the fitness of each individual and retain the best-performing partial individual in the population.

Step 6: To create chaotic sequences by (11), the total number of iterations is k, and the selected position is mapped back to the original solution space by (12). Subsequently, update the best position X .

Step 7: Repetition of the evolutionary cycle and the return to Step 2 until the terminated condition is met.

• C.    CKMTOA PID controller design

PID is an acronym for Proportional–Integral– Derivative, referring to the three terms operating on the error signal to produce a control signal. PID isn’t overly

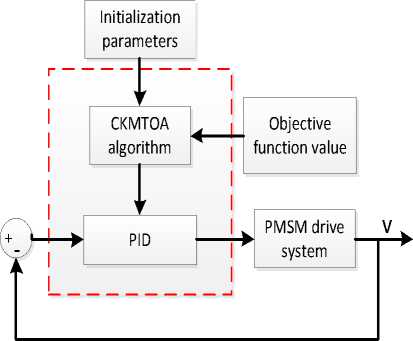
Fig.2. Diagram of self-tuning CKMTOA PID controller.

A self-tuning CKMTOA PID controller is shown in Fig.2. The detailed steps of CKMTOA PID are as followed.

Step 1: Initialize the parameters of algorithm and the swarm by randomly assigning each particle to an arbitrarily initial velocity and a position in three dimension of the solution space. Each individual molecular position consisted of three members KP, KI and KD (three dimensional search space).

Step 2: Calculate the fitness function value in the model of PMSM space vector control system by (15), and select the optimal individual X .

Step 3: Determine that the resultant force of each molecule is attraction, repulsion or zero. Calculate the resultant force between the molecule and the current optimal molecule by (5) or (6). And calculate its acceleration by (7) or (8).

Calculate the objective function value and retain the best-performing partial position

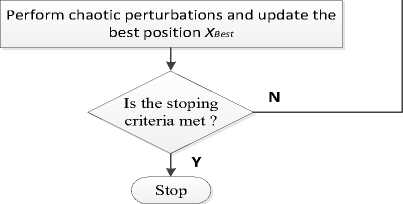
Fig.3. The program flow chart.

Step 4: Update each molecule’s velocity and position by (9) and (10). Update ω of adaptive inertia weight factors according to (13).

Step 5: Calculate the fitness function value of each individual in the model of PMSM space vector control system and retain the best-performing partial individual in the population.

Step 6: Create chaotic sequences by (11), the total number of iterations is k, and the selected position is mapped back to the original solution space by (12). Update the best position X .

Step 7: Stopping condition: If the iteration is equal to the iteration maximum, break to step 8. Otherwise, the procedure is repeated rom Step 2.

Step 8: Output the global optimal fitness function value and corresponding parameters of PID.

The program flow chart of CKMTOA tuning algorithm for PMSM is as follow Fig.3.

• V.    System Simulation and Result Analysis

• A.    Simulation setting

In MATLAB/Simulink environment, the simulation model of PMSM CKMTOA PID parameters self-tuning control system is shown in Fig.4. This control system adopts speed and outer double closed loop control. The inner loop is current loop with classic PI controller. The outer loop is speed loop with CKMTOA PID controller.

In this paper, the parameters of the PMSM used in this simulation are given by table 1.

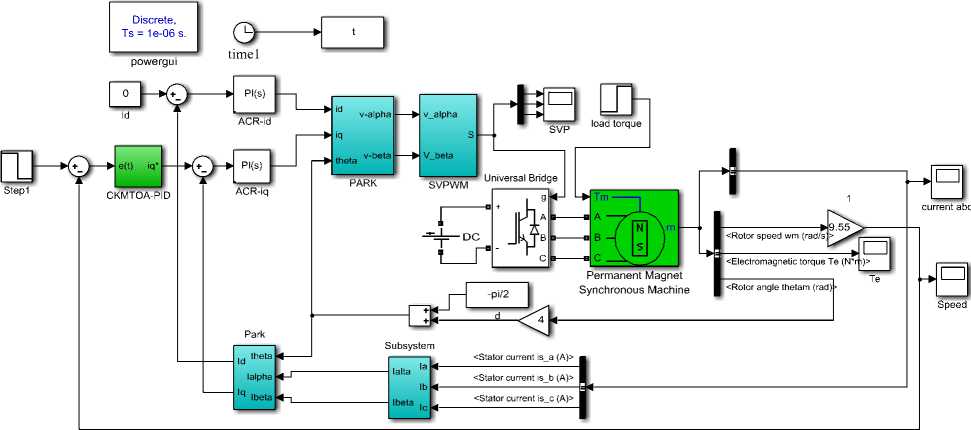
Fig.4. Simulation model of PMSM vector control system with CKMTOA PID controller.

Table 1. The Parameters of the PMSM.

Parameter	Value	Unit
Stator resistance	2.875	Ω
q-axis inductance	0.0085	Н
d-axis inductance	0.0085	Н
Inertia moment	0.008	kg·m^2
Flux linkage	0.175	Wb
Viscous friction coefficient	0.000134	N·m·s/rad
Number of pole pairs	4

The parameters of improved kinetic-molecular theory optimization algorithm has been set as follows: p = 0.3 , p = 0.64 , p = 0.06 . The gravitational constant is G = 2 , the Max iteration number and the population size is set as 50 and 20 respectively. The chaos variable control parameter μ=4. For each iteration we take 20 percent of the population as the current the current partial optimal molecular position. Subsequently, the population is replaced by generating chaotic sequences.

• B.    Simulation Results Analyses and Comparison

  In order to prove the performance of CKMTOA PID optimized controller, a comparison is made between CKMTOA PID, PSO PID and Conventional PID tuned PID controller in the PMSM drive simulation model. The initial condition of simulation is given as follows: the simulation time is 0.2s, the initial speed response from 0 to 2000r/min, then the speed will reduce to 1500r/min in 0.15s, the initially load is 0N·m and rise to 6N·m in 0.05s.

Thespeed response curves of CKMTOA PID, Conventional PID and PSO PID controllers for PMSM drives are shown in Fig.5. It can be seen from Fig.5 that, the speed response of CKMTOA PID controller has small overshoot and it needs a short time to achieve steady state, which is in 0.0059s. However, the Conventional PID and controller PSO PID controller achieve respectively the steady state in 0.0082s and 0.0071s. The adjusting time reduced from 0.0082s to 0.0059s. At the same time, by adopting the self-tuning CKMTOA PID controller is no overshoot. While the load is added and change speed, it shows that the PMSM vector control system with CKMTOA PID controller has the best dynamic behavior, the speed response is the fastest and the speed tracking performance is the best. In summary, for the PMSM control system, the CKMTOA PID controller can improve control accuracy, reduce overshoot and improve response time.

The torque response of PMSM vector control system with CKMTOA PID, Conventional PID and PSO PID controllers controller have been shown in Fig. 6 to Fig.8. From Fig.6 to Fig.8 it can concluded that the PID controller tuned with CKMTOA yields smaller torque ripple. Under the same conditions, the figures show that the CKMTOA PID controller has the best torque control performance. While the command load and speed changes, the CKMTOA PID controller has small overshoot and take shorter time to reach steady-state compared with the Conventional PID and PSO PID controller.

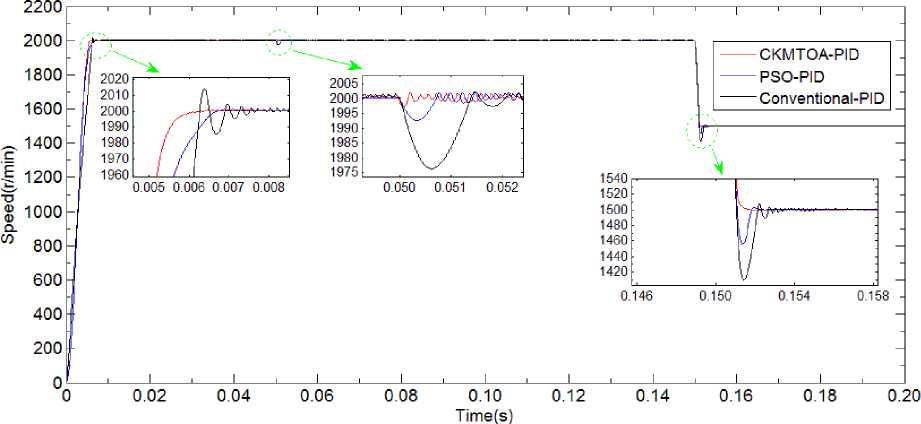
Fig.5. Speed response curve of CKMTOA PID, Conventional PID and PSO PID controller system.

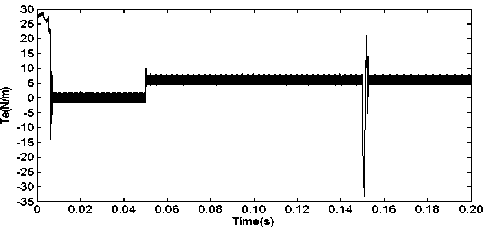
Fig.6. Torque response curve under Conventional PID controller.

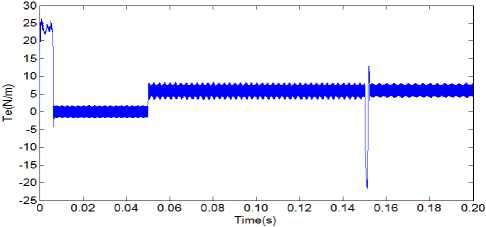
Fig.7. Torque response curve under PSO PID controller.

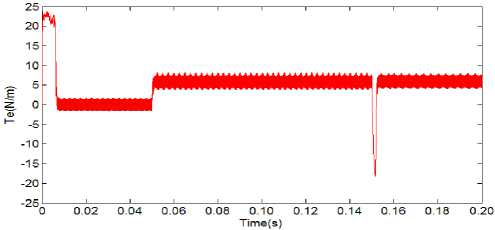
Fig.8. Torque response curve under CKMTOA PID controller.

Applying the Conventional PID controller, the PID controller parameters as follows: K p = 7.7653, K i =0.1856, K_d =0.0124. When applying the CKMTOA PID controller the K_p and K_i is set as in [0,50] and K_d is set as in [0,5] closed interval. After optimization under the same conditions, the optimization fitness function value and the three parameters of CKMTOA PID controller are showed in Fig.9 and Fig.10. The three parameters of CKMTOA PID controller as follows: K p = 16.7304, K i = 0.4544, K d = 0.0628. Finally, the fitness function value is reduced to 0.188.

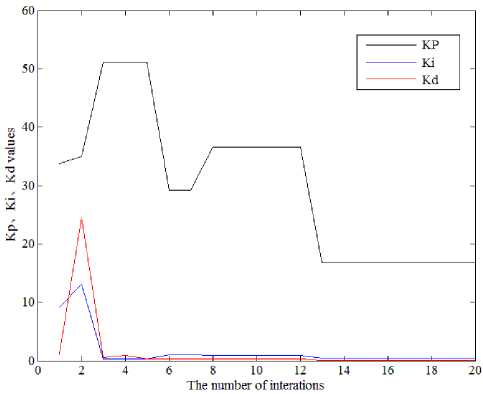
Fig.9. Three coefficients of CKMTOA PID controller curves.

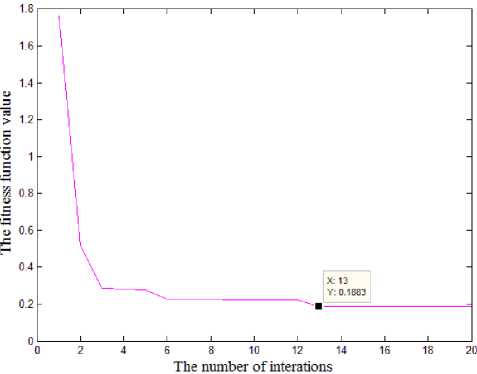
Fig.10. Optimization fitness function value curves.

• VI.    Conclusions

The PMSM vector control is a multivariable, nonlinear and strong coupling system. As a result, conventional PID controller used in vector control system is not satisfied with the requirements of high precision control. In this paper, the PMSM speed control system adaptive PID controller based on CKMTOA self-tuning algorithm is proposed. Making full use of the global optimization ability and self-updating property of improved KMTOA, CKMTOA PID controller can quickly and intelligently select the proper PID parameters. The simulation result shows the CKMTOA PID controller obvious advantages over PSO PID and Conventional PID controller in selfupdating property and global optimization. Under the load and speed variation, CKMTOA PID controller can also reduce the electromagnetic torque ripple so as to make PMSM more stable and robust.

Appendix a Appendix Title

The Research of Improved Kinetic-molecular Theory Optimization Algorithm PID Parameters Self-tuning in PMSM Vector Control.

Acknowledgment

This work was supported by the National Natural Science Foundation of China (61572416), Shenzhen significant         strategy         layout         project

(JCYJ20160429112213821), and Hunan province Natural science Zhuzhou United foundation (2016JJ5033).