Решение электромагнитной обратной задачи восстановления неоднородности в диэлектрическом теле двухшаговым методом по измерениям ближнего поля

Обратные электромагнитные (векторные) задачи восстановления структуры неоднородного тела вызывают большой интерес на протяжении нескольких десятилетий. Одним из наиболее популярных подходов к их решению является минимизация некоторых функционалов ошибок (с помощью регуляризации Тихонова) и использование итерационных методов, требующих выбора хорошего начального приближения.

В данной работе мы используем неитерационный метод к решению обратной электромагнитной задачи восстановления структуры неоднородного тела, на которое падает монохроматическая электромагнитная волна. Задача состоит в нахождении неизвестной диэлектрической проницаемости (или соответствующего ей показателя преломления) ограниченного объемного рассеивателя, расположенного в пространстве, по результатам измерений ближнего поля вне тела. В статье представлено описание, обоснование и применение двухшагового метода.

Сформулирована прямая задача о дифракции монохроматической электромагнитной волны на ограниченном объемном рассеивателе с заданной постоянной магнитной проницаемостью и известной диэлектрической проницаемостью. Исходная краевая задача для уравнений Максвелла сводится к системе, состоящей из сингулярного интегро-дифференциального уравнения электрического поля по области неоднородности и интегрального представления полного электрического поля вне рассеивателя. Приведены основные результаты о разрешимости прямой задачи дифракции.

Затем решается обратная задача, заключающаяся в нахождении неизвестной диэлектрической проницаемости объемного тела заданной формы. Показано, что интегро-дифференциальное уравнение первого рода имеет не более одного решения в конечномерных пространствах кусочно-постоянных функций.

Постановка задачи

Пусть дано некоторое тело Q с К - полушар, ∂ Q – кусочно-гладкая граница. Предполагаем, что диэлектрическое тело Q является изотропным и неоднородным.

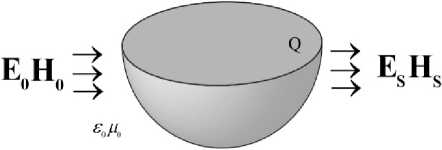
Рис. 1. Графическая иллюстрация задачи

Fig. 1. Graphic illustration of the problem

В пространстве вне тела предполагается, что среда однородна и имеет постоянные значения магнитной проницаемости Ц о и диэлектрической проницаемости S o .

Поле возбуждается точечным источником излучения в точке x о е К ³ \ Q , порождающим электромагнитную волну E ₀ , H ₀ , удовлетворящую системе уравнений Максвелла вне этой точки:

rot H = - i as _nE ,

0      00                                (1)

rot E ₀ = i ^a^ ₀ H 0 .

Полное электромагнитное поле в точке можно представить как сумму двух компонент: падающего поля E ₀, H ₀ и поля E _S , H _S , рассеянного от объекта (рис. 1):

E = E 0 + E s , H = H 0 + H s .                         (2)

Решение прямой задачи дифракции – полное электромагнитное поле E , H – удовлетворяет в К ³ \ d Q уравнениям Максвелла:

rotH = - irosE, rotE = iro^H.

Предполагаем, что на границе раздела двух сред выполняются условия непрерывности касательных компонент поля на границе области неоднородности:

[ E Ш Q =[ H ]| ₅ Q =^0,                            (4)

условия конечности энергии в любом ограниченном объеме пространства:

E , H е L ₂ , l oc ( К ³).                                            (5)

Подробная постановка задачи (1)–(5) и исследование ее разрешимости имеются в [1].

Краевую задачу (1)–(5) можно свести [1] к системе, состоящей из интегро-дифференциального уравнения по области неоднородности:

E ( x ) — ( k 2 + grad div) j_q G ( x , У )( s r ( y ) - 1) E ( y ) dy =       (6)

= Eo(x), x е Q, и интегрального представления поля вне тела:

E ( x ) = E 0 ( x ) +                                               (7)

+ (k2 + grad div) j G(x, У)(sr (y) - 1)E(y)dy, x е К3 \ Q, где ik o|x - y |

G ( x , y )= ^e ,

4n|x- y | а sr = s / So - относительная диэлектрическая проницаемость.

Магнитное поле всюду выражается через электрическое по формуле

H =---- rot E .

i ац о

Введем в области Q вектор-функцию

J ( x ):=( s r ( x ) - 1) E ( x ), предполагая, что всюду в Q выполнено условие |sr ( x )| > S >1. Тогда из представления поля вне рассеивателя получим уравнение для J ( x ):

(к о + grad div) jqG( x, y )J( y) dy =(8)

= E(x) - Eo(x), x е D, а уравнение в области неоднородности перепишем в виде

—Jx - (ко + grad div) G(x, y)J(y)dy =(9)

s r (x) -1

= E _o( x ), x е Q .

Для решения обратной задачи нахождения неизвестной диэлектрической проницаемости (или соответствующего ей показателя преломления) ограниченного объемного рассеивателя, расположенного в пространстве, по результатам измерений ближнего поля вне тела применим двухшаговый метод [2–3]. Первый шаг двухшагового метода заключается в решении линейного интегрального уравнения первого рода относительно тока поляризации (по известным значениям падающего поля E ₀( x ) и полного поля E ( x ) в некоторой области D вне тела необходимо найти ток J ( x ) в Q из уравнения (8)). На втором шаге s ( x ) явно выражается через известную функцию J ( x ) с использованием уравнения (9).

Численная реализация двухшагового метода подробно описана в [4–7]. Ниже представлены результаты расчетов этим методом в случае тела в форме полушара.

Рис. 2 демонстрирует решение прямой (слева) и обратной (справа) задач для полусферы, содержащей неравномерно распределенные неоднородности с различными показателями преломления, значения которых отображены на цветовой шкале. Неоднородности визуализированы цветными фигурами внутри полусферы. Из рис. 2 видно, что

Физика волновых процессов и радиотехнические системы Physics of Wave Processes and Radio Systems

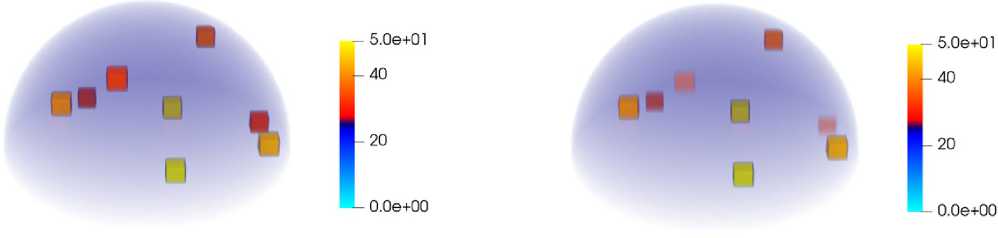
Рис. 2. Решение прямой и обратной задачи для тела формы полусфера

Fig. 2. Solving the direct and inverse problem for a hemisphere-shaped body

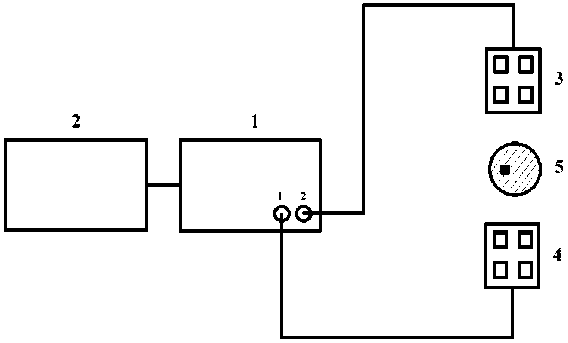
Рис. 3. Схематичное представление измерительной установки

Fig. 3. Schematic representation of the measuring unit

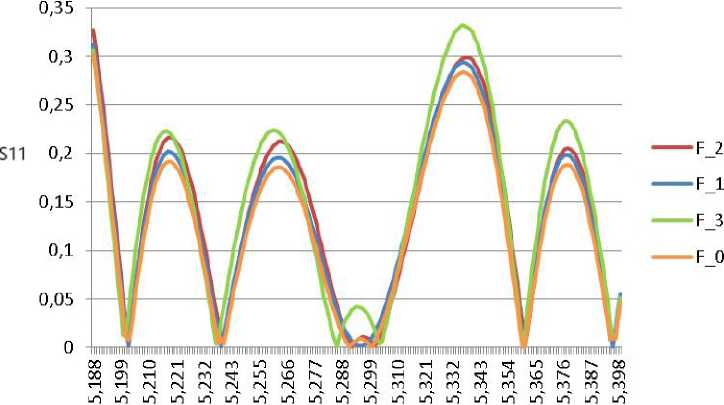
Частота, GHz

Рис. 4. Значение параметра S11 для объектов F ₀ , F ₁ , F ₂ , F ₃

Fig. 4. Value of the S11 parameter for objects F ₀ , F ₁ , F ₂ , F ₃

изменения значений неоднородностей в прямой (точные значения) и обратной (вычисленные приближенные значения) задачах незначительны. Восстановленные данные, отражающие их положение и параметры неоднородности, хорошо различимы.

На рис. 3 представлена принципиальная схема измерительной установки, реализованная с использованием двухпортового векторного анализатора цепей (vector network analyzer) ZNLE6 производства компании Rohde&Schwarz ( 1 ) и персонального компьютера для анализа и обработки

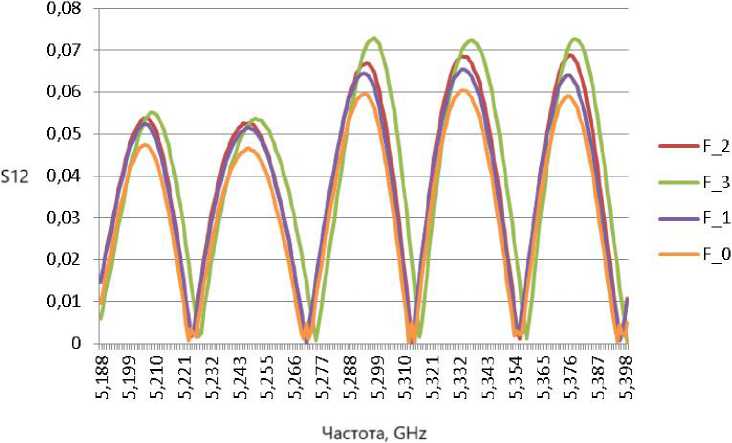
Рис. 5. Значение параметра S12 для объектов F ₀ , F ₁ , F ₂ , F ₃

Fig. 5. Value of the S12 parameter for objects F ₀ , F ₁ , F ₂ , F ₃

полученных измерений ( 2 ). Измерения проводились в диапазоне частот от 5 до 5,5 ГГц с применением микрополосковых печатных антенн, которые направлены друг на друга ( 3 ) и ( 4 ). При проведении измерений исследуемый образец с некоторой неоднородностью внутри ( 5 ) помещается между двух антенн. Объектами исследования являются полусферы с наличием внутри неоднородностей различных размеров: кубических неоднородностей со сторонами 1, 2, 3 см и эталонный объект с однородной структурой. Ниже эти варианты обозначены, соответственно, F ₁, F ₂, F ₃, F ₀.

На рис. 4 и 5 представлены значения модуля вещественной части измеренных коэффициентов отражения и прохождения при помещении объектов с неоднородностями и без. Из графиков видно, что значения параметров заметно изменяются в зависимости от размера неоднородности. Также проводились эксперименты при изменении положения неоднородностей (поворот образца), показывающие изменение S-параметров и в этих случаях.

Экспериментальные данные выявляют принципиальную возможность обнаружения неоднородностей в диэлектрическом теле с помощью измерений электромагнитного поля в ближней зоне.

Заключение

В статье рассмотрен метод решения электромагнитной обратной задачи СВЧ-томографии по измерениям ближнего поля, то есть восстановления структуры неоднородного диэлектрического тела по значениям электромагнитного поля вне этого тела с помощью измерительной установки. Для решения обратной задачи применялся двухшаговый неитерационный метод.

Приведенные численные результаты в случае тела в форме полушара показывают возможность достаточно точного восстановления структуры неоднородного тела по измерениям поля вне тела.

Экспериментальные данные, полученные с помощью измерительной установки, демонстрируют возможность обнаружения сравнительно небольших по размеру произвольно расположенных неоднородностей в диэлектрическом теле посредством измерений электромагнитного поля на различных частотах в ближней зоне.

Финансирование

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ по гранту Государственного Задания (Рег. № 124020200015-7).