Решение краевой задачи для равновесного плавного n- n +-перехода с помощью интерполяционного метода

1. Постановка задачи

ⁿh ⁿi / ⁿe ,

Рассмотрим слой полупроводника толщиной a . Направим ось x декартовой системы координат перпендикулярно его границам. Будем предполагать, что в кристалле присутствует донорная примесь, причем концентрация ионов донорных атомов N_d является функцией x .

В состоянии равновесия токи дрейфа и диффузии электронов проводимости в полупроводнике компенсируют друг друга

где n_i – концентрация электронов проводимости в полупроводнике i -типа.

Введем обозначения:

ea

^E = kT E ’ n e = qn e ’ ⁿi = q— , NN d = qN d .

•w nh = qnh,

Нормировочный множитель для концентраций

заряженных частиц в кристалле

dn je = ец eneE + eDe —e = 0. dx

q =

22 ea

kT s _q

Здесь j_e и E – x -компоненты плотности тока свободных электронов и напряженности внутреннего электрического поля в полупроводнике; n_e – концентрация электронов проводимости; e – абсолютное значение заряда электрона. Коэффициент диффузии D_e и подвижность ц _e свободных электронов связаны соотношением Эйнштейна [1]

С учетом (2), (4), (5) уравнения (1), (3) прини-

мают вид

dn i _e dx

•w dE dix

•w

—in _eE ,

1 s

•w

—n e

+

Я ²

-i - + N ( 5c ) , n e      ^{d (} ) ’

где 5 c = x / a . На поверхностях полупроводнико-

kT

D e       ^ц е ,

e

где k – постоянная Больцмана; T – абсолютная температура полупроводника.

Третье уравнение Максвелла может быть записано следующим образом dE = — [-ne + nh + Nd (x)] .               (3)

dx S q S

вого кристалла, как и во внешнем пространстве, напряженность внутреннего электрического поля равна нулю. Это дает граничные ус-

ловия

EE ( q ) = EE ( 1 ) = q                                        (8)

Здесь n h - концентрация дырок; S q — электрическая постоянная; s — относительная диэлектрическая проницаемость полупроводника. В состоянии равновесия справедливо соотношение

для системы дифференциальных уравнений (6), (7). Равенства (8) вместе с уравнением Максвелла (3) приводят к условию электрической нейтральности полупроводника

a

J p (x) dx = 0, где

Р = e ( ^- n e + n h + N d )

– плотность заряда в кристалле.

^{( x}m <  ^x <  ^xm + i ) ,

( m = o, i,

, M - i ) ,

F m ²⁾ ( x ) = f mm ²⁾ i -[ f m- i ( x m

-

xm

i I - ¹+

2. Интерполяционный метод решения дифференциального уравнения

+

f m ( x m - i

-

xm

) ^{- i} ] ( x

-

xm

i ^{) +}

Для решения краевой задачи (6)–(8) восполь-

+

f m - i ⁽ x m

-

xm

i )   ^{( x}m + i

-

xm

i ) ■ ' +

зуемся интерполяционным методом с переменным шагом. При использовании постоянного шага данный метод изложен в [2].

В случае интерполяции по двум и трем точкам применимы многочлены Ньютона первого и второго порядка [3]

+

S4

f m+ i (

x ( x

^{( x}m

-

xm

) ^{( x}m + i

-

xm

) ^{- i} +

-

^xm + i )   ^{( x}m

^xm - i ) ^{( x}

-

^xm ) ,

-

^xm + i

x

i <  x <  x m + i ) ,    ( m = i,2,

, M - i ) ,

Z ^{( i )} ( x ) = z о + A i ( x o , X i ) ( x - x о ) ,

где

Z ^{( 2 )} ( x ) = Z ^{( 1 )} ( x ) + A 2 ( x o , x i , x 2 )( x - x o )( x - x i ) .

f m^Q ) = f ^{[ x}m ^, y'

Здесь A i ( x o , x i ) и A 2 ( x o , x i , x 2 ) — разделенные

( Q = i,2; m = Q - i, Q ,..., M ) .

разности, определяемые равенствами:

В результате получаем следующие рекуррент-

^A i ( ^x 0^{, x} i ) = ( z i ^- z o )( ^x i ^{- x} o ) ^{- i} A 2 ( x o , x i , x 2 ) = ( x 2 - x o ) ^{- i} x X [A i ( x i , x 2 ) - A i ( x o , x i ) ] =

ные соотношения для определения значений не-

известной функции в точках x_m :

⁽ Q ), = V^ Q )     ( Q )f⁽ Q )     ( Q )

^ym + i ^ym ⁺ m f m + i ⁺ m ,

= z o ( x i ^{- x} o ) ⁱ ( x ^{- x} o ) ⁱ +

( Q = i,2; m = Q - i, Q ,

, M -1 ) .

+ Z i ( x o - x i ) ⁱ ( x 2 - x i ) ⁱ +

Здесь использованы следующие обозначения:

+ Z 2 ( x o - x 2 ) ⁱ ( x i - x 2 ) ⁱ

( Q ) y_m

= y ( x m ) ,    ( Q = i,2; m = o,i, ^ , M ) ,

Интерполяционные многочлены

Z ^{( i )} ( x ) , Z ^{( 2 )} ( x )

( i )

Am

= 2 ( ^xm + i

-

^xm ) ^,

удовлетворяют условиям:

Z ⁽ Q ) ( x j ) = Z j ,    ( Q = i,2; j = o,i,..., Q ) .

в ^{( i )} = ⁱ f⁽ⁱ⁾ ( m   2 f m ⁽

-

^xm ) ,

Рассмотрим дифференциальное уравнение

первого порядка dy = f (x, y).

dx

Разобьем область определения неизвестной функции y ( x ) на M интервалов ( x_m , x_{m +} i ) , ( m = o,i, ..., M - i ) , в общем случае имеющих различную длину. Проинтегрируем уравнение (9) на интервале ( x_m , x_{m +} i )

xm + i ym+i = ym) + J f [x, y (x)] dx, xm

( Q = i,2; m = Q - i, Q ,..., M - i ) .

Подставим вместо функции f [ x , y ( x ) ] интерполяционные многочлены Ньютона первого и вто-

рого порядка

F m ) ( x ) = f m

_ [ /^{(i )}

I f m ( x m + i

X-i

^{- x}m )   ⁺

( m = o,i, _ , M ) ,

m   ( x m + i

-

xm

i )   ^{( x}m + i

-

xm )

x

x

m

-

в^{( 2)} = — f^{( 2 )}

^um     6 f m - i ⁽ x m

^{x ( x}m + i

^{x ( x}m + i

-

xm

,

i )   ^{( x}m + i

-

xm

i ) " ' x

-

xm

-

)3+fm2) (

m

-

^xm - i )

x

+ f m + i (

m

^xm + i )    ^{( x}

-

^xm ) ,

„ ^xm + i ⁺ „ ^xm 63

( m = i,2, _ , M ) .

В случае равномерного

-

2 ^xm - i

,

разбиения области

определения неизвестных функций

m

= m A,    ( m = o, i, ^ , M ) ,

^A = ^{( x}M

-

x o ) / M

равенства (10) переходят в интерполяционные

формулы Адамса [2]

_y ^{(i )} -_y^{( i)}+^{A ( i)} _{+ f} ^{(i )} y m + i y m ⁺ 2 ( f m ⁺ f m + i ) ^,

( m = o, i,

, M -1 ) ,

У ( 2 ) _ у ( 2 ) ₊ А     ( 2 ) ₊gf^{( 2 )}₊5f( ^{2 )}

y m + 1 y m ⁺ 12 ( f m - 1 ⁺ 8 f m ⁺ 5 f m + 1 ) ,

( m = 1,2,..., M - 1 ) .

• 3.    Решение краевой задачи интерполяционным методом

В случае дифференциальных уравнений (6), (7) соотношения (10) записываются следующим образом:

Граничное условие (8) в точке 5 с = 0 дает

E о = E 0 ¹ ) = E 0 ^{2 )} = о.

Представленные ниже решения краевой задачи соответствуют первому из выражений (15), которое содержит знак «плюс» перед квадратным корнем.

Алгоритм решения краевой задачи может быть построен следующим образом. Сначала задается произвольное значение нормированной

⁽ Q ) . = й⁽ Q ) n e , m + 1    n e , m

-

( Q ) ⁽ Q )    г ⁽ Q )      ⁽ Q 2

ⁿm n e , m + 1 m + 1 ⁺ n , m ,

( Q = 1,2; m = Q - 1, Q , _ , M - 1 ) ,

концентрации электронов проводимости в точке 5 г = о

•W

•W

г ⁽ Q )      p ⁽ Q )

E m + 1 = E m ⁺

^—e ,0 = —

( 1 ) e ,0 .

^{( Q} ) 1

⁺ A m

-

⁽ Q ) n e , m + 1

+

V

—i у (Q) ne, m+1

A

^{+ N} d , m + 1

J

+ B EQm ^, (13)

Затем определяются величины й _e 1 = й' E E 1 = EE 1 ¹ ) по формулам (15), (14). Полагая

( 2 ^{( 2 )} - ^^{( 1 )}

^—e ,1 = ^—e ,1 ,

E 12 ) = E 1‘> ,

( Q = 1,2; m = Q - 1, Q ,..., M - 1 ) .

можно выразить

•w

значения n

Величины A m ) , B nQm , B Em , ( Q = 1,2; m = 1,2, - ,

= E mm неизвестных функций

e , m в

M - 1) определяются равенствами (11), в кото-

рых следует положить

f ⁽ Q ) = /2 Q )          ⁽ Q ) г ( Q )

f m      f n , m    f n n e , m , m ,

f^{( Q} ) = ( Q^Q )              ^{( Q} )

f m      f E , m    f E l ^xm , n e , m J,

( Q = 1,2; m = 1,2, ..., M - 1 ) , f n ( n e , E ) = - n e E ,

f E ( x , n e ) = ¹

- n e

~ 2

-i - + N_a ( x ) .

— e     d ⁽ )

e ,1 и

= п' ' Е = ne,m, m точках 5с m,

( m = 2,3, „., M ) , каждое из которых, очевидно, является функцией переменной й_e о . Граничное условие (8) в точке 5 г = 1 дает уравнение для определения й_e о

EE M ( in e ,0 ) = 0-

Решив его, следует повторить описанную выше

процедуру для отыскания истинных значений нормированных концентрации электронов проводимости й _em и напряженности внутреннего электрического поля E_m в точках 5с_m , ( m = 1,2, „., M ) .

( Q )

Выражая E^x_m + 1 из (12), имеем

(Q)     (Q) _y(Q) , г (Q) _ ne, m + n, m ne, m+1 m+1 =     Д (Q Ы Q)       ,

A m n e , m + 1

( Q = 1,2; m = Q - 1, Q , _ , M - 1 ) .

Подстановка (14) в (13) приводит к квадратно- ( Q ) му уравнению относительно неизвестной — e m + 1 -

Его решения имеют вид:

( Q ) n e , m + 1

2 ( Am³ ) ) ²

- 1

x

• 4.    Результаты расчетов

При выполнении расчетов выбирались следующие числовые значения параметров. Толщина слоя полупроводника a = 0,1 мм; относительная диэлектрическая проницаемость полупроводника 8 = 12, 5 (материал полупроводника — кремний); температура кристалла T = 300 К; концентрация электронов проводимости в кремнии 16   –3

i-типа —i = 1,45 ■ 10 м . Предполагалось, что концентрация донорных ионов в ———+-переходе распределена по закону x /б + А(Q)     (Q) + B(Q) + A(Q)N/i      + x^8 + Am 8 I Em + BE, m ) + Am Nd, m+1 —

N d ( x ) = N 0 + N 1 exp

-

a

x

±

где N ₀ = 10²² м ³, N 1 = 10²³ м ³, X = 10 мкм. Под границей раздела — - и — ⁺ -областей понималась плоскость x = x гр , на которой переменная составляющая функции N d ( x ) оказывается в 3

а = 10 раз меньше своего максимального значения N1. Исходя из условия exp

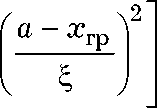
^, а

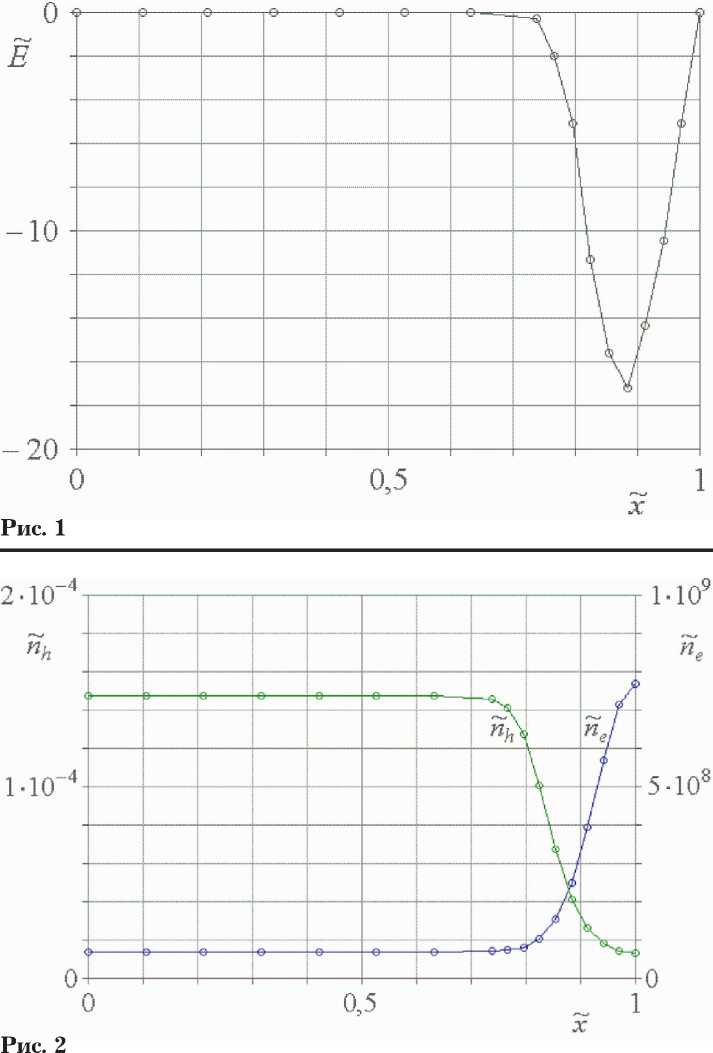
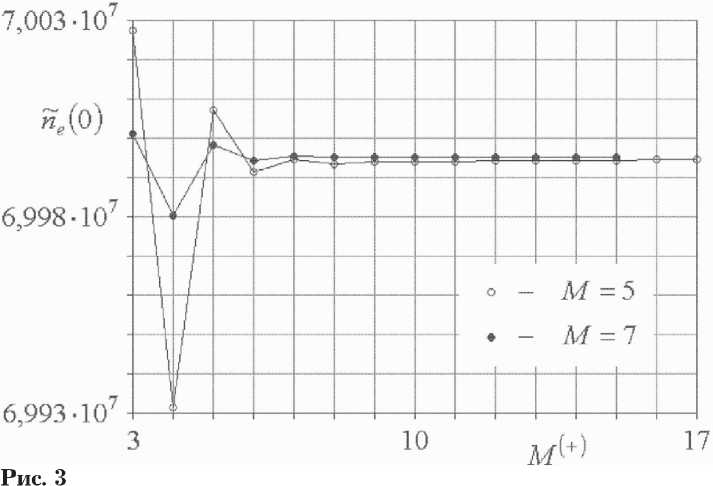
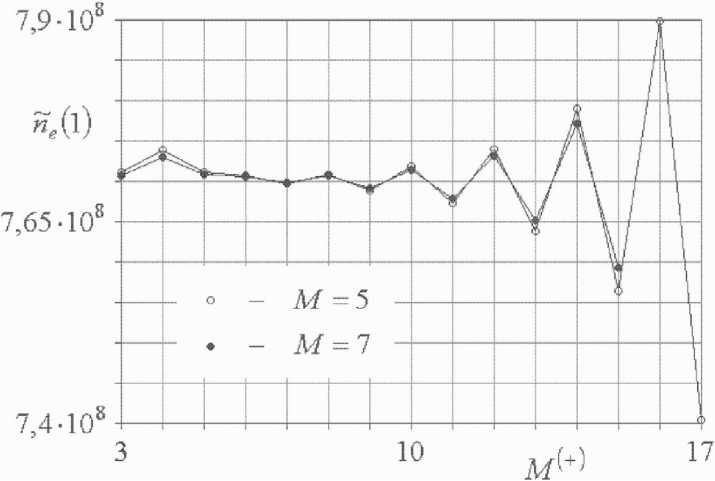
Рис. 4

имеем xгр = a - §Vln а, или

• 5 гр = 1 - § V ln а,

где 5сгр = xгр / a, § = § / a. В процессе реализации интерполяционного алгоритма интервалы (о < 5с < Xгр) и (5гр < 5 < 1), соответствующие n- и n+-областям, разбивались на M и M(+) равных отрезков длиной А = 5гр / M и А(+) = (1 - 5сгр) / M(+). Этим обусловлена необходимость использования интерполяционных фор- мул с переменным шагом.

На рис. 1 изображено распределение нормированной напряженности внутреннего электрического поля в n-n ⁺ -переходе. Здесь количество разбиений n - и n ⁺ -областей составляет: M = 7, M ⁽⁺⁾ = 9. Экстремум функции E ( 5 ) локализован вблизи максимума производной dN д / d5 .

Координатные зависимости нормированных концентраций электронов проводимости n e и дырок n h представлены на рис. 2. Следует отметить, что при выбранных числовых значениях параметров функция п e ( 5 ) с достаточно высокой точностью совпадает с распределением нормированной концентрации донорных ионов в полупроводнике N д ( 5 с ) .

Рис. 3 и 4 представляют собой диаграммы сходимости последовательностей приближенных значений нормированной концентрации электронов проводимости n e на поверхностях слоя полупроводника 5 = 0 и 5 с = 1. Здесь количество разбиений n -области остается фиксированным ( M = 5 или M = 7 ) ; количество разбиений n ⁺ -области M ⁽⁺⁾ варьируется. Начиная с некоторого значения параметра M ⁽⁺⁾ , решение краевой ( 2 )

задачи найти не удается. Корни n_{e , m} квадратного уравнения, определяемые равенствами (15), становятся комплексными. В случае M = 5 и M = 7 это происходит соответственно при M ⁽⁺⁾ = 18 и M ⁽⁺⁾ = 16.