Решение нестационарной краевой задачи внутренних магнитогидродинамических волн на поверхности раздела слоев проводящей жидкости

В статье поставлена и решена нестационарная краевая задача, о внутренних магнитогидродинамических волнах на. поверхности раздела слоев проводящей жидкости в скрещенных электрическом и магнитном полях. Задача, поставлена в безиндукцион-ном и линейном приближении для идеальной несжимаемой жидкости. Поставленная начально-краевая задача, решена, аналитически путем применения методов операционного исчисления и интегральных преобразований Фурье. В явном виде получено уравнение волновой поверхности раздела, слоев, позволяющее определить критическое положение, при котором не происходит захвата стратифицированной жидкости из другого слоя.

Электромагнитные способы обогащений тесно связаны с магнитогидродинамическими задачами о слоистом течении проводящей жидкости в скрещенных электрическом и магнитном полях. При этом необходимо прежде всего определить критическое положение поверхности раздела, т. е. такое положение, при котором не происходит захвата жидкости из других слоев [1-3].

В случае, когда жидкость забирается из нижнего слоя, критическое положение поверхности раздела называется верхним положением (рис. 1), а при заборе из верхнего слоя — нижним положением (рис. 2).

В прямоугольной системе координат xOz часть пространства, ограниченная условиями 0 ^ ж ^ Z, 0 ^ г ^ Hi, представляет верхний слой несжимаемой проводящей жидкости, другая часть пространства — 0 ^ х ^ I, —Н^ ^ z ^ О — нижний слой (Z — длина ванны, Hi и Н^ — глубины слоев, ось z — направлена вверх, плоскость z = 0 совмещена с поверхностью раздела слоев). Оба слоя жидкости помещены в скрещенных однородных электрическом и магнитном полях. Созданная электромагнитным полем пондеромоторная сила направлена вертикально сверху вниз и создает возможность гравитационного всплывания частиц примеси из нижнего слоя в верхний. Очищенный от примеси нижний слой жидкости через заборное окно вытекает из ванны. Заборное окно ограничено условиями х = 0, — Н^ ^ z ^ — Н^ + h, где /г — высота окна. Для сохранения постоянных уровней слоев полагается, что в нижнем слое при х = I по всей глубине размещены источники с суммарной мощностью равной расходу

жидкости через заборное окно. Жидкость считается идеальной, движение — безвихревым (потенциальным).

z

ρ ₁ , σ ₁

l

-;

x

14::

ρ ₂ , σ ₂

h

Рис. 1.

В безиндукционном и линейном приближении сформулированная контактная задача магнитной гидродинамики сводится к решению дифференциальных уравнений Лапласа

z

ρ ₁ , σ ₁

x

14::

ρ ₂ , ₂

l

Рис. 2.

£^i + d²ii Эх² dz²

^£1 ₊ ^^Р²

Эх2 dz2

О при 0 ^ z ^ Д1,

О при — Н₂ ^ z ^ О

при следующих начальных и граничных условиях:

^ilt=o- 9t

= 0, t=0

1          8<р2

= 0 t=o

5^1 Эх

= 0, ж=0

5^1 Эх

= 0, ж=/

5^2 Эх

ж=0

-ГИ = {

— Уо о

при — Н₂ ^ z ^ — Н₂ + /г, при — Н₂ + h < z ^ 0,

5^2 Эх

Х=1

4U

Н2 ’

Pi^- + i+9iPiHi=O при z = Hi.

d^i dz

^- при z = 0.

OZ

ц

d\i ЭЕ

+ 784^+81^7)-д

ЁуД ЭЕ

) при г = °’ (8)

Эф2 dz

= 0,

z = -H2

где приняты следующие обозначения: фуД,г,1) и (рДх^Д^ — потенциалы скоростей в верхнем и нижнем слоях соответственно, р^ и р^ — плотности, tri и ст2 — электропроводности в верхнем и нижнем слоях жидкости,

(Ю)

91 — 9 4-- -EqB₀, g* _ g -\-- -EqBq, pl                    P2

Eq = Еу — напряженность электрического поля, Bq = В_х — индукция магнитного поля.

Относительно граничного условия (6) отметим, что волнообразование на свободной поверхности верхнего слоя не учитывается.

Волновая поверхность раздела слоев при z = 0

или

ЧИЛ =

+

ЭрД, В) dt

91     5^1

Р292 — Р191 91

<71^

92^2

^^^^^^^^.

pig*i

^1

ДрДхДтД dz

^^^^^^^^™

z=0

^^^^^^^^.

Р2 дф2

Р292 — Р191 9t

ct^Bq

92^2

^^^^^^^^.

Р191

^2

(ДДдШД dz

z=0

I

Для непроводящей жидкости эта задача поставлена и решена в [4].

Приступая к решению поставленной начально-краевой задачи (1)—(9), применим интегральное преобразование Лапласа относительно времени t.

+ <х>

<91,₂(ж, z,p) = j ip_li2(x,z,t)e"^pt dt. о

В результате преобразования (13) выражения (1)-(9) в изображениях запишутся следующим образом

/ХфгД^) = 0,

А№(ж, z) = О,

	dpi Эх	ж =	= 0, =0	dpi dx	X-	= 0, =z
Эр2			VH	dip2
Эх	= x=0		p :	dx	X-
Pippi + criBypi			+ ^ = 0 p			при z = Hi
			dpi dz	_ dp2 dz		при z = 0,

Pi 7 2 , ^1 D2 A ~ , *dpi A” oPr 91^. -p2 / 2 , ^2 „2 V *d+2 у +ЙВ°РЛ 92"57. при z = 0, (20) dp^ dz = 0. z = -H2 (21) переме-

Применим конечное косинус-преобразование Фурье относительно ной х:

<11,2^7) = j pi^x, z)cos^-x dx, о

(РрЦп dz2

^^^^^^^^.

^a_nPl,n — 0

при

О ^ z ^ Hi,

d^P^n dz2

^^^^^^^^.

^2 ~

® 71^2,71

МоМ

^^^^^^^^.

Z = H1

= KMM

p

HiL

^^^^^^^^.

км

р

при — H^ ^ z ^ 0,

?(p+ ^M)

/*w

Р1,П

z=Hx

= 0 (п= 1,2,3...),

Ni,n   dP2,n

——— = ——— при Z dz dz

= 0,

/ 2 । ^l r>2 A -     । * dpi n pi [p + —BopWi^+gi—,— \ pi /            dz

=Р2

/ 2 | ^2 _п2 \ -

Р + — В_ор ]р₂,_п

V р-2       '

,  * ^2,п

+ 92—1— dz

при z = О,

dp-цп

dz

= О.

z = -H2

Решения дифференциальных уравнений (23) и (24) с граничными условиями (25) и (28) имеют следующий вид:

71,п(Д = СцггбЬ^Д - ЯД),

72,ДД = с_{2 n} ch ДДг + ЯД) + — а_1г

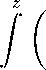
Нг

ИНГ

р

^^^^^^^^.

^^ sh Д_пД

Р /

Постоянные щ и с2 определяются из граничных условий (26) и (27).

Для С1_)П и С2,_п получаются следующие выражения:

А^

С1,п

рМр + ^У J (шли

-я2 \

-™) ch (аДЯ. + ДИ

Ф ch (a„Hi) сЬ(а„Я₂) + /), sh (е„Н₂) sh (а„Я,)) (р² + sp + g)

A^

C2,n

_ а^Вр ch (а_пЯД ch (а_пЯД + a^B^ sh (а_пЯД sh Д_пНД

' p2 ch (аиЯД ch (аиЯД + pT sh (аиЯД sh (аиЯД '

=     (m2 - P\g*^an 8Ь(апЯ2)сЬ(апЯД p2 ch (апЯД ch (anH2) + pY sh (апЯД sh (апЯД ’

(сЬ(апЯД

о

-p^p^I- И^-^_ЫЫ

V p2 ' a_n J \ p p )

-H2

+ p2g₂ (--- ) ch (а,Д) d^

-H2

+ Pi

p(p + —вЛ v Pi '

sh ДпНх)

- g{a_n ch (a_n НД

о

^/(3 y.......M)

H2

x 7---------------------------------------------\------------

|^p₂ ch Д_пН_х) ch <а_пН^ + p_x sh Д_пН_х) sh (a_nH₂^ (p² + sp + g)

I

В результате применимых интегральных преобразований (13) и (22) выражение (12) принимает вид

Дф\,п

РРп = —;— dz

I

2=0

Подставив выражения (29) и (31) в (34), получим

^*

Лп =

ch(a_nHi)p₂(p+ ^В^а_п

( Р2 ch ДпНх) ch (a_nH₂) + p-v sh (а_иНД sh (а_пН₂) ]р(р² + sp + у)

где

( 1|"Г/ о?о = 0, аи = --------sh(anH2)--sh (anh) (n = 1, 2, 3 ...).      (36)

Для f]n обратное косинус интегральное преобразование Фурье имеет сле дующий вид

ОО

Т^Р) = V У^7/_и(р)сО8й_иЖ.

71=1

Для нахождения оригинала функции ?/(жД) достаточно использовать таблицы операционного исчисления.

Уравнение волновой поверхности раздела слоев получается в следующем виде о ОО

/         2 П7Г

№ И = ?/_n(t)cos—ж,                   (38)

71=1

где

Рп^ =

сЪ^а^Ну

dn^q

^^^^^^^^.

s2

Р2«п

Г е 2 sin a q

^^^^^^^^.

4 '

sjq- ^cos ^q- ^t q

+

dn = p-2 ch (a_nHi) ch nH^ + pi sh (a_nHi) sh (a_nH₂).          (40)

С точки зрения реализации на ЭВМ целесообразно выражению (39) придать следующую форму:

( л 2У° V"

71=1

(-l)™^ th (ап^) -

sh (an/i) дГДДТП

—e

t

^sin^/^

dn\[b%

^^^^^^^^.

S2

-fan

Ie 2 smygn

^^^^^^^^™

s2

f^

^^^^^^^^™

^ +

= COS

^^^^^^^^.

s2

4 1

Qn

+

V^n-^

9?l

где dn = 1 + — th (апН^ th (anH2), P2

f 1 - ^4th(anH2))

_ *         \ P2 g₂* ^v j

-92Qn1 + ^th(anHi)th(anH2y g2B02 l + ^th(an^)th(a^2)

^Sn Р2 1 + th (а„Я_х) th (а„Я₂)’

X _ -2а_пН_{г                х} _ -2а_пН₂

th Д_пН^ = —--- 7—777, th (а_пЯ₂) = —---77777.

sh (a_nh) ch (а_пЯ₂)

^a_n (H₂ — h)   g — a_n (H₂+h)

h < я₂.

X | g — 2a_nH₂