Решение обратных задач аэродинамики для невыпуклых форм

Основным при решении обратных задач аэродинамики (ОЗА) является определение формы тела по заданному распределению характеристик (в нашем случае скорости) на его поверхности. Обратные задачи, в отличие от прямых, позволяют решить проблему отыскания контура профиля, обладающего заранее заданными свойствами.

Для идеальных несжимаемых жидкостей (ИНЖ) обратная задача обычно сводится к решению интегрального уравнения Фредгольма II рода [1; 4]. Использование данного метода хорошо себя зарекомендовало при отыскании форм крыловых профилей по заданным скоростям на их поверхности [2; 3]. Иногда обратные задачи сводятся к отысканию форм невыпуклых тел [5].

В данной работе на основе интегрального уравнения составлены методы решений прямой задачи аэродинамики (ПЗА) и ОЗА. С использованием данного подхода численно решена задача отыскания формы тела, обтекаемого двумерным потоком ИНЖ, в рамках различных параметризаций профиля. Вычислительные эксперименты позволяют сделать сравнительные выводы об эффективности параметризации, задающей контур.

Постановка задачи

Искомое непроницаемое тело обтекается двумерным потоком ИНЖ с заданной скоростью на бесконечности ^-→ υ _∞ (см. рис. 1). На поверхности задано распределение скорости потока и = и(0),0 € [0, 2п] (см. рис. 2). Требуется определить форму тела.

Данная постановка может быть разрешена интегральным уравнением Фредгольма II рода, которое связывает между собой скорости потока на поверхности профиля и его форму:

и(^ о ) = ¹ / u(0)K(0,0 o )d0 + 2( dx cos(a) + -dy sin(a)), (1) π 0 dθ 0 dθ 0

где ядро K имеет вид

K (9,0 o ) =

^{( y} - y o ) ddx ^{+ ( x -} x) dy (x - X o ) ² + (y - y o ) 2

Здесь a — угол атаки набегающего потока, (x, y) — точки контура тела, скорости нор-мированны относительно скорости набегающего потока υ ∞ .

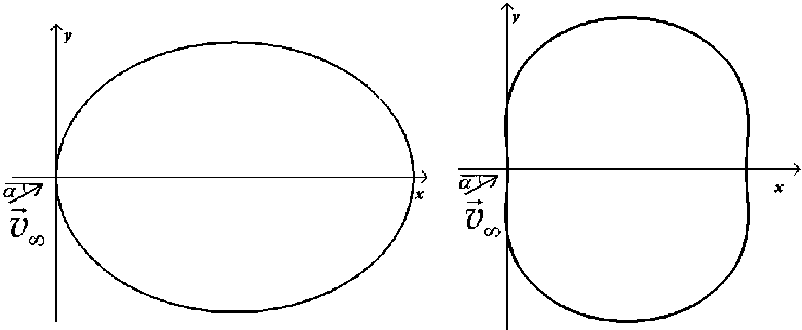
Рис. 1. Формы искомых обтекаемых тел: а — эллиптическое; б — невыпуклое

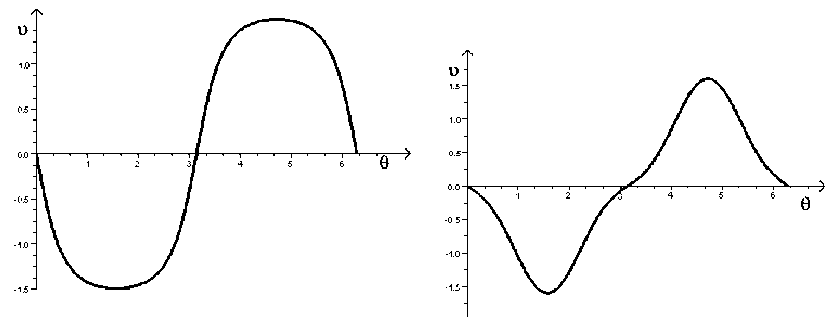
Рис. 2. Распределение скорости, соответствующее телам: а — эллиптическому; б — невыпуклому

Уравнение (1) имеет бесконечное множество решений. Согласно постулату Жуковского — Чаплыгина добавляем условие и(0) = и(2п) = 0 для замыкания системы. Имен- но на базе этого интегрального уравнения далее строятся решения прямой и обратной задач.

Решения прямой и обратной задач

На поверхности тела задается сетка с координатами (x, у). Уравнение (1) с условием и (0) = и(2п) = 0 сводится к системе уравнений в узлах [1; 4]:

Г и о = 0             ‘             ‘

{ ^ AijUj = -2(xi cos(a) + yi sin(a)) ’ где матрица A содержит координаты профиля нелинейным образом.

В работе использаны две различные параметризации координат: (x(6),y (6)) и (г(в ),в)• Первая задается как:

{ x^)   (1 + cos(e))/2 ,6 = 2n/(N - 1), где N число узлов сетки. В этой параметризации происходит сгущение точек в лобовых областях. Вторая задает равномерное разбиение по углу вдоль контура тела (г(в),в), где в изменяется от 0 до 2п.

ПЗА решается разрешением уравнений (3) относительно скорости на поверхности известной формы тела и угла набегающего потока. Нахождение узлов контура профиля из нелинейной системы (3) для заданного распределения скоростей на поверхности дает решенеие ОЗА.

Результаты расчетов

Для тестирования методов была проведена серия расчетов. В качестве исходных данных были взяты распределения скоростей, полученные решением прямой задачи для заданных тел (целевых) (например, см. рис. 1 и 2). Для эллипсов варьировались их толщины (от 0,5 до 1,5), углы набегающих потоков α (от 0 до 15 градусов), бралось различное количество узлов N (80, 160, 320), корректировалось целевое распределение характеристик υ. Исходный профиль, с которого начиналось решение ОЗА, был близким по форме к целевому. Исследования [1; 4] показывают хорошую работу обеих параметризаций для таких тел, но наиболее предпочтительной оказывается (x(6),y(6)).

Для невыпуклых тел (см. рис. 1б и 3а) допустимо задание контура только через (г(в ), в). В работе [1] исследовано решение таких задач. Проведена проверка устойчивости метода к измененным начальным данным. Рисунок 4б соответствует модифицированному распределению скорости для профиля рисунка 3а. В результате решения ОЗА было получено тело, изображенное на рисунке 4а.

Заключение

Каждый из подходов выбора сетки хорош лишь в строго определенных случаях. Выходом из этого положения может стать синтез двух параметризаций в одну, или выбор неравномерного разбиения узлов для случая (r(6), 6).

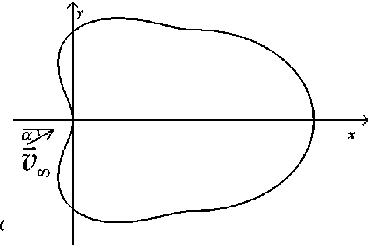
Рис. 3. Пример невыпуклого тела а

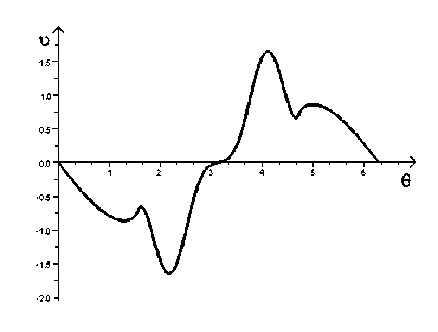
с распределением скорости на нем б

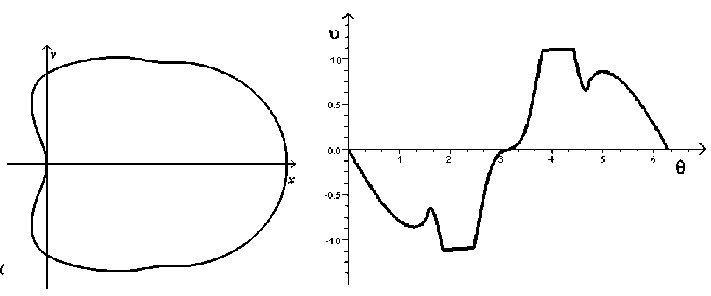
Рис. 4. Пример полученного тела а , соответствующий измененному распределению скорости б