Решение одного нелинейного диофантова уравнения

Диофантовы уравнения - это алгебраические уравнения или системы алгебраических уравнений с рациональными коэффициентами, решение которых отыскивается в целых или рациональных числах (см.: Математическая энциклопедия. М„ 1979. Т. 2. Стб. 168-171). Как правило, число неизвестных в диофантовых уравнениях больше числа уравнений, поэтому они также называются неопределенными уравнениями (подробнее об этом см.: Соловьев Ю. Неопределенные уравнения первой степени И Школа в «Кванте»: Арифметика и алгебра. М., 1994. С. 32 - 40). Решение уравнений в целых числах является одной из древнейших математических задач. И в настоящее время исследование диофантовых уравнений представляет собой пограничную область между теорией чисел и алгебраической геометрией.

Известно, что существует большое число конкретных диофантовых уравнений, решаемых элементарными методами (см.: Серпинский В. О решении уравнений в целых числах. М„ 1961). В общем случае проблема разрешимости диофантовых уравнений - это проблема отыскания алгоритма для распознавания по любому диофантову уравнению, имеет ли оно решение. Столь важная проблема и в настоящее время остается открытой и не исследованной до конца. Все известные методы и способы для распознавания наличия решений у диофантовых уравнений приме-

W$&^^             4(2)

нимы лишь к уравнениям из отдельных более или менее широких классов. Далее в статье будет описан способ решения нелинейных диофантовых уравнений конкретного вида, часто возникающих при решении задач олимпиадного типа.

Интересно отметить, что с диофантовыми уравнениями связана глубокая теорема Зигеля о целых точках, т.е. теорема о конечности числа решений в целых числах одного класса диофантовых уравнений (см.: Математическая энциклопедия. Т. 2. Стб. 456 -457). Мы будем вести речь о рациональных (не обязательно целых) решениях конкретного диофантова уравнения второй степени, прежде заметив, что в общем случае нахождение всего множества рациональных точек для конкретной кривой, заданной диофантовым уравнением, - очень трудная задача (см.: Васильев Н.Б., Гутенмахер В.Л.. Раббот Ж.М., Томм А.Л. Заочные математические олимпиады. М., 1987. С. 34 - 36.)

Рассмотрим нелинейное (второй степени) диофантово уравнение, симметричное относительно вхождений переменных хи у:

аху - Ь(х + у) = с.          (I)

Здесь а, Ь, с - целые числа, причем а отлично от нуля.

Если h = с = 0. т.е. Ь² + с² = 0. уравнение (I), очевидно, имеет единственное рациональное решение (0; 0).

Если Ь² ^ с²> 0, то описываемый ниже способ нахождения рациональных корней дает все рациональные решения уравнения (1).

Определение. Любую упорядоченную пару целых (рациональных) чисел (х_и, у₍₁), удовлетворяющую уравнению (1), будем называть его /-решением (Q-решением).

Для любых целых Ь, с и ненулевого целого а из уравнения (1) справедливо представление ca + b2 _ kxlx _kd2 _ _ У»!

Нетрудно убедиться, что справедлива следующая теорема.

Теорема. Только пары чисел вида

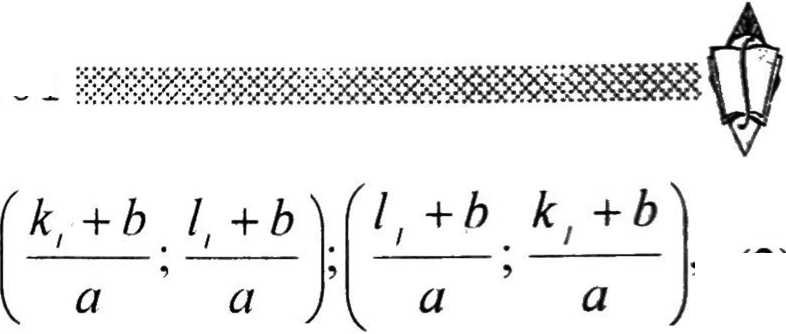
’ (2)

где j = 1, пт, образуют весь спектр Q-pe-шений диофантова уравнения (I).

Замечание 1. Ясно, что по формулам (2) попутно находится и весь спектр /-решений уравнения (I), если он не пуст.

Пример 1. Решить уравнение

Зху - 2(х + у) = 29.

Решение.

са+b² _29-3+2² _91_ 1-91 _7-J3_91-1 _ 13-7 а² " З²          З² " З²"" З² " З²

получаем пару (I; 31).

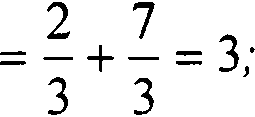
получаем пару (3,5).

91 2

х, ---ь — = 31;

получаем пару (31; I).

2 13

Х4 = Т + ~

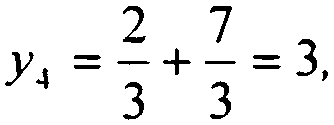
получаем пару (5; 3).

Таким образом, у исходного уравнения существуют только целые Q-решения. Т.е. /-решения исчерпывают весь спектр решений исследуемого уравнения.

Ответ: (1: 31), (3:5). (31: 1),(5:3).

Замечание 2. Очевидно, что все Q-решения уравнения

Р г /   XS

• -•^₇(х + т) = — q к        m

где р, q, г, s, m - целые числа

(q, k.m* 0), так же можно найти с помощью изложенного выше алгоритма.

Замечание 3. Для решения системы уравнений ахху -bx (х + у) = сх, а2х2 + b,xy + с2у2 = d,

Щ ^щ^^^ ИНТЕГРАЦИЯ где av bv cv aY К, cY d - целые числа (a, * 0; a^ + ^2 + c2 > 0), сначала необходимо найти все Q-решения первого уравнения этой системы, а затем выделить среди них те, которые удовлетворяют второму уравнению.

Пример 2. Решить систему уравнений (Зху-2(х + у) = 29, \3х²+2ху + 4у² = 97.

ОБРАЗОВАНИЯ ^^^^

Решение. Подставим решения, найденные в примере 1, во второе уравнение исходной системы:

312 — 2-1 -31 + 4-3I2 ^97, З-З2-2-3-5 + 4-52=27-30 + 100 = 97. 3-312 — 2-1 -3 1 + 4-312 ^97, 3-52 - 2-3-5 + 4-32 ^97,

Как видим, подходит лишь одна пара чисел (3; 5). Это-7-решение исходной системы.

Ответ: (3; 5).