Решение олимпиадных задач методами дискретной математики
Автор: Мухаметова М.И., Воистинова Г.Х.
Журнал: Международный журнал гуманитарных и естественных наук @intjournal
Рубрика: Педагогические науки
Статья в выпуске: 6-2 (81), 2023 года.
Бесплатный доступ
В статье раскрыты некоторые приемы решения олимпиадных задач средствами дискретной математики. Подчеркивается преимущество владения разными методами и способами решения таких задач и определение оптимального из них. Олимпиадные задачи требуют нестандартного подхода. Успешно участвовать в олимпиаде по математике может учащийся, знакомый не только со стандартными способами решения задач, но и приемами, выходящими за рамки школьного курса.
Олимпиадные задачи, методы решения, графы, комбинаторика
Короткий адрес: https://sciup.org/170199567
IDR: 170199567 | DOI: 10.24412/2500-1000-2023-6-2-163-168
Текст научной статьи Решение олимпиадных задач методами дискретной математики
Олимпиадные задачи по математике – термин для обозначения круга задач, для решения которых обязательно требуется неожиданный и оригинальный подход.
Решение олимпиадных задач принципиально отличается от решения школьных, даже очень сложных, задач. Это обусловлено, прежде всего, выбором разделов, традиционно рассматриваемых на олимпиадах. Теория игр, графы, уравнения в целых числах и т.д. не рассматриваются в школьном курсе математики, не говоря о принципе Дирихле, элементах теории чи сел и комбинаторики, логических задачах. И чем больше методов, способов и приемов решения олимпиадных задач ученик знает, тем больше его шансы успешно выступить на олимпиаде.
Какая же задача называется нестандартной? Л.М. Фридман дал следующее определение: «нестандартные задачи – это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения» [7]. Однако следует заметить, что понятие «нестандартная задача» является относительным. Одна и та же задача может быть стандартной или нестандартной, в зависимости от того, знаком ли школьник со способами решения задач такого типа. Таким образом, нестандартная задача – это задача, алгоритм которой неизвестен, т.е. неизвестен ни способ её решения, ни то, на какой учебный материал опирается решение. А некоторые задачи требуют еще и специальных знаний, подготовки. К таким задачам относятся задачи на смекалку, на логику, применения инвариантов, задачи на раскраски, на чет и нечет и т.д. Конечно, для успешного решения любой задачи нужно уметь думать, догадываться, но этого мало. Нужны знания и опыт в решении задач. Полезно владеть и определенными общими подходами к решению таких задач. Поэтому мы решили разобраться в решении этих задач, попробовать их исследовать, найти общие подходы. Любая задача должна чему-нибудь научить. Решение каждой задачи должно быть шагом вперед в развитии математических знаний, умений и навыков, должно обогащать знания и опыт, учить ориентироваться в различных ситуациях.
При подготовке к математической олимпиаде, часто учащиеся сталкиваются с проблемой, каким методом решать задачу. Хотелось бы найти метод, который был бы интересен, с помощью которого можно было бы решить широкий круг задач.
Метод графов
Графический способ содержит в себе метод, основанный на теории графов. Этот метод показался интересным и увлекательным. Однако теория графов не рассматривается в школьном курсе математики, но широко используется в решении олимпиадных задач. Давайте рассмотрим этот метод подробнее.
Граф – это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (рёбра графа). Вершины, из которых выходит нечетное число ребер, называют нечетными вершинами, а вершины, из которых выходит четное количество ребер – четными.
Решая задачу про кенигсбергские мосты, Эйлер установил свойства графа:
-
1. Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.
-
2. Граф с двумя нечетными вершинами тоже можно начертить одним росчерком. Движение нужно начинать от любой нечетной вершины, а заканчивать на другой нечетной вершине.
-
3. Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.
-
4. Число нечетных вершин графа всегда четное.
-
5. Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф будет равно половине числа нечетных вершин этого графа.
Выделяют несколько типов задач, решаемых методом графов:
-
1. Задачи на вычерчивание фигур одним росчерком.
-
2. Логические задачи.
-
3. Задачи о мостах.
-
4. Задачи о «правильном» раскрашивании карт.
-
5. Задачи о колодцах.
-
6. Задачи на построение уникурсальных графов.
-
7. Задачи комбинаторного характера.
Рассмотрим задачи, которые можно решить методом графов.
Задачи на вычерчивание фигур одним росчерком
Фигуры, которые можно будет вычертить одним росчерком, в математической и методической литературе называют Эйлеровыми графами [7]. Чтобы решить задачи данного типа следует знать свойства графа, рассмотренные выше.
Например, у фигур 1 и 5 (рис. 1) все вершины четные, поэтому данную фигуру можно начертить одним росчерком (свойство 1), у фигур 2, 3, 6 имеется две нечетных вершины, но (по свойству 2) и их можно начертить, если начать с одной из нечетных вершин. А вот фигуры 4 и 7 нельзя начертить одним росчерком, так как у них более двух нечетных вершин [5].
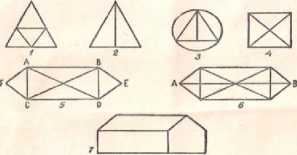
Рис. 1. Эйлеровы графы
Задача 1 . Начертить одним росчерком следующие фигуры (рис. 2).
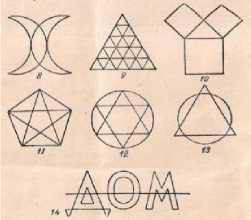
Рис. 2. Эйлеровы графы
Логические задачи
При решении логических задач следует выделить группы объектов и элементы к ним относящиеся – вершины графа, далее из условия задачи устанавливаем между ними отношения – ребра графа. Если отношения неконкретные, то ребра рисуем пунктирной линией, если конкретные, то сплошной линией.
Задача 2. В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько ещё осталось [4]?
Решение: В данной задаче одна группа – игроки. Поэтому устанавливаем отношения между игроками (рис. 3).
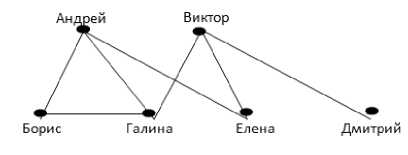
Рис.3. Граф проведенных игр
Посчитав количество ребер, ответим на вопрос, сколько игр сыгранно к настоящему моменту.
Ответ: 7 игр.
Построим граф для непроведенных игр (рис. 4), на этом рисунке граф имеет 8 ребер, следовательно, осталось провести 8 игр.
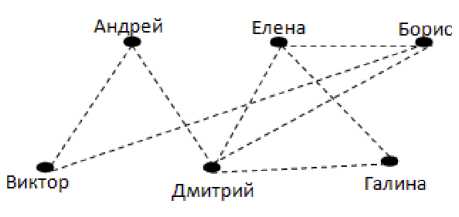
Рис. 4. Граф непроведенных игр
Задача 3. Купленные в подарок игрушки (пистолет, сумочку, куклу и машину) уложили в четыре коробки, по одной игрушке в каждую. Требуется узнать, что положено в каждую коробку, если известно следующее: машинка и пистолет не в красной коробке; коробка с сумочкой находится между синей коробкой и коробкой с куклой; в зеленой коробке не сумочка и не машинка; желтая и зеленая коробки находятся около коробки с пистолетом [5].
Решение: Построим граф, рассуждая следующим образом. По условию машина и пистолет не в красной коробке – соединим эти вершины штриховыми линиями.
Известно, что коробка с сумочкой не синяя, соединим эти вершины штриховой линией. Сумочка и машинка не в зеленой коробке, тоже соединяем соответствующие вершины штриховыми линиями. Пистолет не в желтой и не в зеленой коробках, соединяем также эти вершины штриховыми линиями.
Становится очевидным, что пистолет лежит в синей коробке, соединяем соответствующие вершины стрелкой. Теперь становится очевидным то, что машина находится в желтой коробке. Сумочка лежит в красной коробке, а кукла в зеленой (рис. 5).
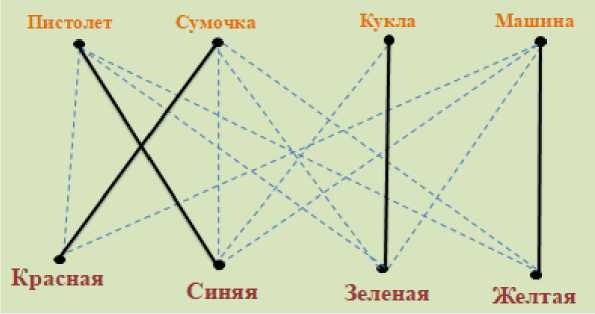
Рис. 5. Граф решения
Ответ: Пистолет – в синей, сумочка – в красной, кукла – в зеленой, машинка – в желтой коробках.
Методы комбинаторики
Основной вопрос комбинаторики – «сколько?», основная задача – подсчёт числа элементов конечного множества.
В комбинаторных задачах нас обычно интересует, сколько комбинаций, удовлетворяющих тем или иным условиям, можно составить из заданного конечного набора объектов. Как отмечают методисты [1, 2], в простейших случаях мы можем выписать все нужные нам комбинации и непосредственно подсчитать их. Однако при бессистемном выписывании легко упустить какую-то комбинацию или, наоборот, посчитать некоторую комбинацию дважды. Поэтому при переборе вариантов желательно придерживаться двух правил.
-
1. Обозначаем наши комбинации буквами или цифрами так, что каждая комбинация будет обозначена своей уникальной последовательностью букв или цифр.
-
2. Выписываем комбинации в алфавитном порядке (при обозначении буквами) или по возрастанию чисел (при обозначении цифрами). При таком переборе ни один вариант не ускользнёт от нас и, с другой стороны, будет исключена возможность повторения вариантов.
Задача 4. Маша собирается съесть яблоко, сливу и мандарин, но пока не решила, в какой последовательности. Сколькими способами Маша может выбрать эту последовательность?
Решение: Обозначаем буквами: Я – яблоко, С – слива, М – мандарин. Тогда, например, СМЯ – это вариант, когда Маша сначала съест сливу, потом – мандарин, потом – яблоко. Выпишем варианты в алфавитном порядке:
МСЯ, МЯС, СМЯ, СЯМ, ЯМС, ЯСМ.
Получилось 6 вариантов.
Задача 5 (Задача Леонарда Эйлера). Четыре гостя при входе в ресторан отдали швейцару свои шляпы, а при выходе получили их обратно. Невнимательный швейцар раздал шляпы случайным образом. Сколько существует вариантов, при которых каждый гость получил чужую шляпу [8]?
Решение: Пронумеруем гостей цифрами 1, 2, 3, 4 и так же пронумеруем их шляпы. Считаем, что шляпа с данным номером принадлежит гостю с этим же номером (то есть, например, шляпа 2 принадлежит гостю 2). Тогда каждый вариант получения шляп обозначается четырёхзначным числом, составленным из цифр 1, 2, 3 и 4, в котором номер позиции цифры есть номер гостя, а сама цифра есть номер полученной им шляпы (номера позиций будем считать слева направо).
Например, комбинация 4132 означает, что первый гость получил четвёртую шляпу, второй – первую, третий – третью, а четвёртый – вторую. Такой вариант не годится по условию, поскольку третий получил свою шляпу. Теперь понятно, что нужно сделать – выписать по возрастанию все четырехзначные числа, содержащие по одной цифре 1, 2, 3 и 4, такие, что никакая цифра не стоит на позиции со своим номером.
Эти числа выписаны ниже под чертой (рис. 6). Красные цифры над чертой – но- мер позиции (номер гостя), с которым не должна совпадать цифра в соответствующем столбце (номер шляпы).
Как видим, всего имеется 9 вариантов нужной раздачи шляп. Вариантов может быть довольно много, но в некоторых случаях, тем не менее, самый быстрый способ решения задачи – разумно организованный перебор.
12 3 4
214 3
23 4 1
24 13
314 2
34 12
34 2 1
412 3
43 12
-
43 2 1
Рис. 6. Комбинации шляп и гостей
Заключение. Мы рассмотрели некоторые нестандартные методы и приемы, которые будут полезны при решении олимпиадных задач. Моделирование условия задачи с помощью графов позволяет устанавливать различные связи и отношения между данными и искомыми величинами задачи, позволяет лучше осознать идею решения, его логику, увидеть различные способы решения задачи. Также составление графов является увлекательным занятием.
По мнению Г.Х. Воистиновой и Л.З. Зариповой [1, с. 114], методы дискретной математики используются при решении олимпиадных задач, которые требуют детального анализа условия и требования задачи, представляющих собой дискретные объекты, такие как целые числа, графы, комбинаторные объекты и т.д. Они позволяют разбить задачу на более простые компоненты и применять математические методы для их решения. Кроме того, методы дискретной математики могут помочь определить оптимальные решения и оценить сложность алгоритмов. В целом, использование методов дискретной математики позволяет решать олимпиадные задачи более эффективно и быстро.
Список литературы Решение олимпиадных задач методами дискретной математики
- Барболин М. Головоломки и графы // Научно-популярный физико-математический журнал "Квант". - 1994. - № 6. - С. 33.
- Березина Л.Ю. Графы и их применение: Пособие для учителей. - М.: Просвещение, 2001 - 143 с.
- Виленкин Н.Я. Комбинаторика / Н.Я. Виленкин [и др.]. - М.: МЦНМО, 2013. - 180 с.
- Воистинова Г.Х., Зарипова Л.З. О нетривиальном приеме решения олимпиадных задач по математике // Математическое моделирование процессов и систем: Материалы XII Межд. молодежн. науч.-практ. конф. Часть 1, 17-19 ноября 2022 г., г. Стерлитамак / отв. ред. С.В. Викторов. - Стерлитамак: Стерлитамакский филиал УУНиТ, 2022. - С. 110-115.
- Горбачев В.Г. Сборник олимпиадных задач по. - М., 2004. - 56 с.
- Мельников О. И. Теория графов в занимательных задачах. - Изд. 3-е. - М.: КомКнига, 2009. - 232 с.
- Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Книга для учащихся ст. классов сред. шк. - М.: Просвещение, 1989. - 192 с.
- Яковлев И.В. Комбинаторика для олимпиадников. - М.: МЦНМО, 2014. - 80 с.


