Решение проблемы Аргунова - Глисона

Паппову плоскость изучали Штаудт, Штейнер, Шаль, Гильберт, Глаголев, Гуревич и др. Дезаргову плоскость впервые описал Гильберт в [1]. Проективную плоскость, в которой выполняется проективно малая теорема Дезарга D 10 О L 10 , изучали Руфь Муфанг [10], Скорняков [11], и др. (эти плоскости называются муфанговыми). Проективную плоскость, в которой проективно выполняется конфигурационная теорема Фано 7 з , изучал Глисон [6]. Он доказал, что конечная плоскость Фано дезаргова и, следовательно, паппова. Бесконечную плоскость Фано изучали Глисон, Рашевский [10], Скорняков [11], Аргунов [2]. Аргуновым и Глисоном была поставлена следующая проблема: «Не дезаргова ли бесконечная плоскость Фано?». В настоящей работе получено полное описание бесконечной плоскости Фано и, следовательно, решение проблемы Аргунова — Глисона.

• 1.    Необходимые сведения

Определение 1.1 [3]. Классическая алгебраическая система A(+, • ), в которой имеют место аксиомы

• (1 ) A(+) — абелева группа,

• (2 ) A0\{ O } есть IP-лупа,

• (3 ) (a + b)c = ac + bc (a, b, c),

• (4 ) a(b + c) = ab + ac (a, b, c), называется альтернативным телом .

Теорема 1.1 (Линник) [4] .    Всякое альтернативное тело характеристики 2

ассоциативно.

Конфигурационная теорема Фано 1.1 (7 з ) [6]. Пусть для точек 1,2, 3, 4 общего положения выполняются инциденции: 6 = [1,4] П [2, 3], 5 = [1, 2] П [3,4], 7 = [1, 3] П [2,4] . Тогда будет выполняться и инциденция (5, 6, 7) .

Определение 1.2. Проективная плоскость, в которой проективно выполняется теорема 7 з , называется плоскостью Фано.

Определение 1.3 [2, 7]. Конфигурационная теорема K1, содержащая все инциденции теоремы K | и еще хотя бы одну дополнительную инциденцию каких-то элементов K | в плоскости G p характеристики р, называется частным случаем теоремы K | , в плоскости G p . Конфигурационные теоремы K и R в плоскости G p называются эквивалентными проективно-алгебраически, если они или их частные случаи K i и R i соответственно даже при отсутствии R и K или одной из них в плоскости G p в своем исходном виде, имеют одну и ту же совокупность локальных алгебраических эквивалентов.

Определение 1.4 [7]. Совокупность всех общих и ограниченных квазитождеств теоремы K и ее следствий K i в плоскости G p , называется проективным алгебраическим эквивалентом теоремы K в тернаре плоскости G p .

Определение 1.5 [7]. Классическая алгебраическая система A(+, • ), в которой выполняются следующие условия:

• 1)    A(+) — абелева группа,

• 2)    A0 \{ O } — лупа,

• 3)    a(b + 1) = ab + a ( V a, b,)

• 4)    (a + 1)b = ab + b ( V a, b),

• 5)    уравнения x = bx + c и ta = tb + c, a = b, однозначно разрешимы относительно x и t называется слабо-дистрибутивным телом.

• 2.    Решение проблемы Аргунова — Глисона

В бесконечной плоскости Фано имеют место, кроме 7 з , нижеследующие конфигурационные теоремы, геометризующие характеристику 2.

Конфигурационная теорема 2.1 (Dp) [7]. Если для точек (3,6,1 0 ), 2 0 ,4 бесконечной плоскости Фано выполняются следующие инциденции:

• [1 0 ,3]    п [4,2 0 ] =2, 3 0 = [6,2 0 ] п [3,4], 5 = [2 0 ,3] п [1 0 ,3 0 ], 1 = [1 0 ,4] п [2 0 ,5], 7 = [1 0 ,2 0 ] п [1,2],

то будут выполняться и инциденции (5, 6, 7) и (3, 3 0 , 7) .

Очевидно, что D p = D(8; 10,10) = Dp в плоскости Фано содержит замыкающиеся конфигурации 7 3 { 1234 } , 7 | { 1 0 2 ⁰ 3 0 3 } , 7 3 { 1 0 2 0 34 } , 7 | { 11 0 22 ⁰} , 7 5 { 1 0 357 } и что Dp = 7 з { 1 0 2 ⁰ 3 0 3 } и { 4,2,1 } = { 1 0 ,2 0 ,3 0 , 3,5,6,7,4 } . 2 = [4,2 0 ] п [6,3], 1 = [4,1 0 ] п [2 0 ,3] п [7,2] } .

Поскольку D p содержит все инциденции D 9 (рис. 3) и инциденцию (7, 3,4), то она есть частный случай D 9 в плоскости Фано.

Теорема 2.2 [7] . В плоскости Фано G | из 73 следует Dp.

Конфигурационная теорема 2.3 (L p ) [7]. (A) Пусть в плоскости Фано для точек 7,4, 2 0 , 3,1 (рис. 2), выполняются инциденции:

1 0 = [4,1] п [2 0 ,3], 3 0 = [4,3] п [2 0 ,7], 5 = [1 0 ,2 0 ] п [4,7],

6 = [4,7] п [1 0 ,3 0 ], 2 = [3,7] п [4,2 0 ].

Тогда будут выполняться инциденции (1, 3, 6) и (1, 2, 5, 3 0 ) , другими словами, (A 0 ) : пусть для точек (5, 3, 1 ⁰ ), 4, 2 имеют место инциденции [5, 3] п [4, 2] = 2 ⁰ , [5, 2] п [4, 1 ⁰ ] = 1, [5,4] п [2, 3] = 7 , [2 0 , 7] п [3,4] = 3 0 , [1, 3] п [1 0 , 3 0 ] = 6 . Тогда будут иметь место и инциденции _ _ _ _ _ _

(4, 5, 6) и (1, 2, 3 0 ) .

Теорема Lp содержит все инциденции L 9 (123; 1 0 2 0 3 0 ) (рис. 4) и инциденцию (1, 2, 3 0 ), и поэтому, она есть частный случай L 9 .

Связи между L p и 7 з выясняет следующая

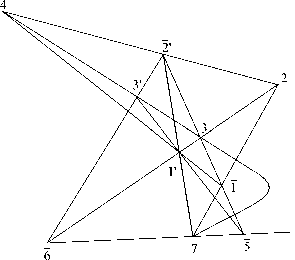
Рис. 1. (D ₈ ^∗ )

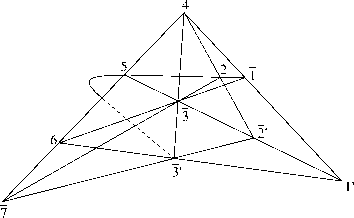
Рис. 2. (L 8^∗ )

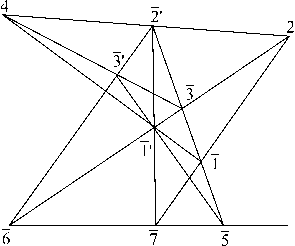
Рис. 3. (D 9 )

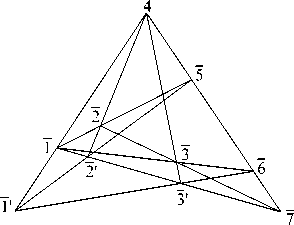
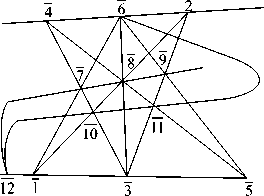
Рис. 4. (L 9 )

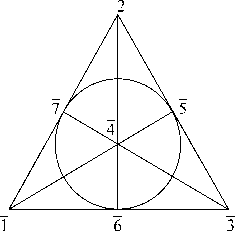
Рис. 5. (П ^∗7 )                                    Рис. 6. (7 3 )

Теорема 2.4 [7] . В плоскости Фано из 7 з следует Lg.

Теорема 2.5. Теорема D g проективно эквивалентна теореме Lg.

Сформулирована необходимая для дальнейшего исследования, конфигурационная теорема с двумя замыкающими инциденциями, содержащая пары перспективных трехвершинников.

Конфигурационная теорема 2.6 (Щ) (рис. 5). Пусть в плоскости Фано заданы точки 1, 3, (2,4, 6) и выполняются инциденции: 7 = [1, 6] П [3, 4], 8 = [1, 2] П [3, 6] , 5 = [4,8] п [1,3], 9 = [5,6] п [2,3] , 9 = [5,6] п [2,3] , 10 = [3,4] п [1,2] , 11 =_[2,3] п [4,5] , 12 = [10,11] П [1, 3] . Тогда выполняются и инциденции (10,11,12, 6) и (8, 9, 7,12) .

Теорема 2.7 [7] . В плоскости Фано из D g следует Щ проективно.

Нахождению аксиоматики тернара бесконечной плоскости Фано посвящена следующая основная теорема.

Теорема 2.8. Некоторыми квазитождествами теоремы 7 з являются:

• 1)    a + (a + k) = k, q + (c + p) = c + (p + q) ( V c,p, q);

• 2)    a + b = b + a ( V a, b);

• 2 0 )    a + (b + c) = (a + b) + c ( V a, b, c);

• 3)    a • m о am = am + am = 0 ( V a, m);

• 4)    a • m о b = d ^^ a • m о d = b ( V a, b, d, m);

• 5)    q • n о q = qn + q ( V q, n);

• 6)    a • m о (am + am • m) = am • m ( V a, m);

• 7)    a(r + 1) = ar + a ( V a, r);

• 8)    aa ^{- 1} = a - 1a = 1 ( V a = 0);

• 9)    1 • q о q = 1 • c о q ( V c, q);

• (1)    s • p о (s + ac) = s + s • p о ac ( V s,p, c, a);

• 10)    < (2) p • f о (c • f о d) = c • f о (p • f о d) ( V p,f, d, c)

• (3)    aq • k о (aq • q о ac) = aq • q о (aq • k о ac) ( V a, q, k, c);

• 11)    a • m о b = am + b ( V a, m, b);

• 12)    a(k + ak) = ak + a • ak ( V a, k);

• 13)    a • a ^{- 1}c = c ( V a = 0, c);

• 14)    a(a - 1c + c) = c + ac;

• 15)    ca • a ^{- 1} = c ( V a = 0, c);

15 0 ) ca • (a ^{- 1} + c) = c + ca • c; a(a ^{- 1} + b) = 1 + ab;

• 16)    (a + 1)k = ak + k ( V a, k);

• 17)    (d + dt) = dt + dt • t ( V d, t);

• 18)    a - 1(ab + (b + c)) + a ^{- 1}(ac + (b + c)) = b + c;

• 19)    a(c + d + (a + 1) ^{— 1} (c + ad)) = ac + ad + a • (a + 1) ^{- 1} (c + ad), a • (a + 1) ^{- 1}b = a(a + 1) ^{- 1} • b = (1 + (a + 1) ^{- 1})b, a(a + 1) ^{- 1} = (a + 1) ^{- 1}a,

b(a + 1) ^{- 1} • a = ba • (a + 1) ^{- 1} = b • (a + 1) ^{- 1}a = b • (a + 1) ^{- 1} a = b(1 + (a + 1) ^— 1 );

• 20)    a(d + m) = ad + am ( V a, d, m = ^(a, d));

• 21)    (m + d)a = ma + da ( V a, d, m = ^(a, d));

• 22)    (a + b)c = ac + bc ( V a, b, c);

• 23)    a(b + c) = ab + ac ( V a, b, c);

• 24)    a • bc = ab • c.

C 7з ^ 1)—17) доказаны в работах [7, 8]. Приведем ключевые моменты этих доказательств.

• 1): Следует из Щ : { 5 = (0, c + p), 3 = ( го ), 1 = (0,p + q), 2 = (q,p + q), 4 = (c,c + p) } (рис. 5).

2): Следует из Щ : { 1 = (0,a), 2 = (a, a), 3 = ( го ), 4 = (b, b), 5 = (0, b) } (рис. 5).

2 ⁰ ): следует из 1) и 2).

3): Следует из L8 : { 7 = (m), 4 = ( го ), 3 = (0,am), 2 0 = (a, am), 1 = (am, am + am) } (рис. 2).

4): Следует из 7 3 { ( a, d ) , (0 , d ) , ( го ) , ( m ) } .

5): Следует из 7 3 { 0 , cn ) , (1) , ( го ) , ( c, 0) } .

6): Следует из L g { 4 = ( го ), 1 = (0, 0), 7 = (0), 3 0 = (am, am), 2 = (a, (am) • m) } .

7): Следует из L8 { 7 = (0, 0), 4 = ( го ), 2 0 = (ar, ar), 3 = (a, ar), 1 = (r + 1) } .

8): Следует из { 3 = (a, 1), 7 = (0, 0), 2 0 = (1,1), 4 = ( го ), 1 = (a ^{- 1} + 1) } , где a ^{- 1} есть решение уравнения xa = 1.

9): Следует из 7 з { (0, 0), ( го ), (q), (1, c) } .

10): (1) Следует из 7 з { А = (0, ac), B = (1), C = (р), D = (0, s • р о (s + ac)) } , { р = 1 } .

1о): (2) Следует из 7 з { ( го ), (b, d), (p, d), (f) } , b = p.

10): (3) Следует из 7 з { (0, ac), ( го ), (k), (aq, aq • q о ac) } .

11): Следует из D 8 { 1 = (0,p), 1 0 = ( го ), 2 = (1), 2 0 = (aq, aq • q о p), 3 0 = (a, aq • q о p) } .

12): Следует из L 8 { 7 = (0, 0), 4 = ( го ), 1 = (q), 2 0 = (1,ak), 3 = (a, ak) } (рис. 2).

13), 14): Следуют из L 88 { 7 = (0, 0), 4 = ( го ), 2 0 = (1, c), 1 = (a ^{- 1}c + c), 3 = (a, c) } .

15), 15 0 ): Следуют из L g { 3 = (ca, c), 7 = (0, 0), 2 0 = (1, c), 4 = ( го ), 1 = (a ^{- 1} + c) } .

16): Следует из L g { 7 = ( го ), 4 = (0), 1 = (a + 1, 0), 2 = (1, am), 3 0 = (a, m) } .

17): Следует из L g { 4 = (0), 7 = ( го ), 2 = (d, am), 3 0 = (ac, ac), 1 0 = (0, 0) } .

Докажем теперь соотношения: 7 з ^ 18)-24).

18): 7 з { p—(0,1), 4 = ( го ), 2 0 = (1,c), 3 0 = (a, ac) } ,     _                                     ( * )

A = [p, 4] П [30, 20] = [x = 0] П [y = xc] = (0, 0), B = [p, 20] П [4, 30] = [y = xf +1] П [x = a], 201 о c = f + 1, f = c + 1, B = (a, a(c + 1) + 1), C = [p, 30] П [4, 20] = [y = xs + 1] П [x = 1] = (1, s + 1), 301 о ac = as + 1, s = a-1(ac + 1), C = (1, a-1(ac + 1) + 1), (A, B, C) о BI [A, C] = [y = x(a-1(ac + 1) + 1)] о a 1(a(c + 1) + 1) — a ^(ac + 1) + 1,                           (18.1)

a(a(c + ac + as) + as + ac) = a ¹ • as + as + ac, a(c + ac + as) + as + ac = a(s + as + ac), ac + 1 = as, 1 = as + ac,

a(s + as + ac) + a(c + as + ac) = as + ac.                   (18.2)

Если в (18.1) заменим 1 на 1 + c, то получим:

a (a1 + 1 + c) + a (ac + 1 + c) = 1 + c.                     (18.3)

Доказано соотношение 7 з ^ 18).

19): Пусть образующие точки 7 з имеют следующие координаты: P = (0, c + (1 + a) ^{- 1}(c + ad)) = (0, t o ), 4( го ), 2 0 = (1, c), 3 0 = (a, ac). Тогда получим:

7 з { P, 4, 2 0 , 3 0 } ^ 7 = [4, P] П [2 0 , 3 0 ] = [x = 0] П [y = xc] = (0, 0),

• 2 = [4, 2 0 ] П [P, 3 0 ] = [x = 1] П [y = xf + t o ] = (1,f + t o ),

• 3 0 1 о ac = af + t o ^ f = a ^{- 1}(ac + t o ), 2 = (1, a ^{- 1}(ac + t o ) + t o ),

[2, 7] =jy = x(a - 1 (ac + t o ) + t o )],

• 3 = [4, 3 0 ] П [P, 2 0 ] = [x = a] П [y = xp + t o ] = (a, ap + t o ),

• 3 = (a, a(c + t o ) + t o ),

(2, 3, 7) о a(c + t o ) + t o = a(a 1 (ac + t o ) + t o ),                   (19.1)

a(c + t o ) + t o = a(1 + a) (c + ad) + c + (a + 1)  (c + ad) =

(19.2)

= c + (a + 1) • (1 + a) ^{- 1}(c + ad) = c + c + ad = ad,

• 3 = (a, ad).

Очевидны следующие выкладки: a • (1 + a) ^{- 1}(c + ad) = ((a + 1) + 1) • (1 + a) ^{- 1}(c + ad) = (c + ad) + (1 + a) ^{- 1} (c + ad) = (1 + (1 + a) ^{- 1}(c + ad) = ((a + 1)(a + 1) ^{- 1} + (1 + a) ^{- 1} (c + ad) = a(1 + a) ^{- 1} • (c + ad).

Следовательно, получено следующее равенство:

a(1 + a) ^{- 1}(c + ad) = a(1 + a) ^{- 1} • (c + ad).                     (19.3)

Продолжая алгебраизацию всех других инциденций 7 з , получаем:

• 21 [3, 7] = [y = xd] о a ^{- 1}(ac + t o ) + t o = d ^ 2 = (1, d),

a(c + t o ) + t o = ad, a ^{- 1}(ac + t o ) + t o = d ^ a(c + t o ) + a ^{- 1} (ac + t o ) = ad + d о a • (1 + a) ^{- 1}(c + ad) + a ^{- 1}(ac + c + (1 + a) ^{- 1}(c + ad)) = ad + d о a(1 + a) ^{- 1}(c + ad) + ad + d = (1 + (1 + a) ^)(c + ad) + d+ad = c+ad + (1 + a) ^(c+ad)+ d+ad = c+d + (1 + a) ^(c+ad) ^о a ^- (ac + c + (1 + a) ^- (c + ad)) = c + d + (1 + a) ^- (c + ad),

a(c + d + (1 + a) (c + ad)) — ac + c + (1 + a) (c + ad) — ac + c + (c + ad) + a(1 + a) ^(c + ad) =^ a(c + d + (1 + a) ^(c + ad)) —       (19.4)

• — ac + ad + a • (1 + a) ^{- 1}(c + ad).

Доказано: 7 з ^ 19).

20): L 8 { 4 — ( го ), 7 — (0, 0), 3 0 — (a, ac), 2 — (1, b + c), I — (b) } ^ 5 — [1, 2] n [4, 7] — [y — xb + t] n [x — 0] — (0, t);

2 1 о b + c — b + t ^ t — c, 2 0 — [3 0 , 7] n [4, 2] — [y — xc] n [x — 1] — (1, c),

1 0 — [2 0 , 5] n [4,_1] — [y — xf + c] n U — (f), 2 0 1 о c — f + c ^ f — 0,1 0 — (0),

3 — [4, 3 0 ] n [5,1 0 ] — [x — a] n [y — c] — (a, c),

6 — [1 0 ,3 0 ] n [4, 7] — [y — ac] n [x — 0] — (0, ac),

61 [1, 3] — [y — xb + t ⁰ ], 31 о c — ab + t ⁰ ^ ac — ab + c,

(a + 1)c — ab ^ c — (1 + a) ^{- 1} • ab — ^(a, b),

(2,3,7) о 31 [2, 7] — [y — x(b + c)] о c — a(b + c), a-1c — b + c ^ c — (1 + a-1)-1b — ^(a, b) — (1 + a)-1 a • b,

(1, 2, 5, 3 0 ) о 3 0 1 [1, 2, 5] — [y — xb + c] о ac — ab + c ^ c — ab + ac, c — (1 + a) ^{- 1}ab —

y^{( a,b )}.

Таким образом, из L 8 следует квазитождество a(b + c) — ab + ac, где c — ^(a, b) и потому оно есть правый слабый дистрибутивный закон.

• 21) Пусть образующие точки L имеют следующие координаты: { 4 — (0), 7 — ( го ), 2 0 — (a, am), 3 — (a + b, a), 1 0 — (0,0) } . Тогда, следуя таблице инциденций, соответствущей данному набору образующих точек, получаем:

5 — [4, 7] ^п [1 0 ,_2 0 ] — l ^ ⁿ [y — xm] — (m),

2 — [7, 3] П [4, 2 0 ] — [x — a + b] П [y — am] — (a + b, am),

3 ⁰ — [7, 2 ⁰ ] п [4, 3] — [x — a] п [y — a] — (a, a),

1 — [2, 5] n [1 0 ,4] — [y — xm + t] n [y — 0] — (x i , 0).

21[2, 5] о am — (a + b)m + t ^ t — am + (a + b)m, 0 — xm + t ^ x — tm ^{- 1}.

• 1 — ((am + (a + b)m)m ^{- 1},0) — (x ₁ ,0),

6 = [1 0 , 3 0 ] n [4, 7] — [y — x] n u — (1) I [1, 3, 6] — [y — x + t ⁰ ],

3I[1, 6] о a — a + b + t ⁰ ^ t ⁰ — b,

11[1,6] о 0 — x ₁ +1 ⁰ ^ t ⁰ — x ₁ о b — (am + (a + b)m)m ^{- 1} о bm — am + (a + b)m, ( * )

(1, 2, 5, 3 0 ) о [1, 2, 5] 13 0 о [y — xm + am + (a + b)m] о a — am + (a + b)m + am о a — (a + b)m,

(10,20, 3,5) о [10,20,5] 13 о [y — xm] 13 о a — (a + b)m ^ am-1 — a + b, a(1 + m-1) — b, < a — b(1 + m-1)-1 — b • (1 + m)-1m

(a + b)m — am + bm — a, am + a — bm, a(m + 1) — bm, a — bm • (m + 1)-1 — b(1 + (m + 1)-1) — b(1 + m)-1m.

Следовательно, (b + a)m — bm + am не есть общий дистрибутивный закон, и тем самым доказана импликация L8 ^ 21).

22): Новый набор образующих точек L g , имеющих координаты 7 — ( го ), 4 — (0), 1 — (ba + b, 0), 2 — (b, ba • m), 3 0 — (ba, bm), приводит к получению квазитождества (p + q)k — pk + qk, V p, q, k.

В самом деле произведя алгебраизацию всех инциденций L ^∗ ₈ , получаем:

2 ⁰ — [7, 3 ⁰ ] n [4, 2] — [x — ba] n [y — ba • m] — (ba, ba • m).

_ _ _ _ _ _ _ _ _ _ _ _

5 = [4, 7] n [2,1, 3 0 ] = U П [y = xf + t] = (f),

2 I о ba • m = bf + t 3 0 1 о bm = ba • f + t

^ ba • m + bm = ba • f + bf ^ m = f, 5 = (m),

• 1 1 о 0 = (ba + b)f + t ^ t = (ba + b)f = (ba + b)m) ^ bm + ba • m = (b + ba)m. ( * * * )

(p + b)m = (b • b - 1 p + b)m = (b • b - 1p) • m + bm = pm + bm;

1 0 = [5, 2 0 ] n [4, ²] = [y = xm +1 ⁰ ] n [y = 0],

2 0 1 о ba • m = ba • m + t⁰ ^ t⁰ = 0, 1 0 = (0, 0),

3 = [5, 2 0 ] n [4, 3 0 ] П [7, 2] = [y = xm] П [y = bm] П x = b] = (b, bm),

6 = [4,7] n [1 0 ,3 0 ] = U n [y = xs] = (s),

3 0 1 о bm = ba • s ^ s = (ba) ^{- 1}(bm) = ^(a, b, m), V a, b, m,

6 1 [1, 3] = [y = xs + r],

1 1 о 0 = (ba + b)s + r

3 I о bm = bs + r

bm = bs + (ba + b)s о

(ba + b)s = ba • s + bs, V a, b,m, s = ^(a, b • m) о ( *** ).

Итак, из L ^∗ ₈ следует 22).

23): Опираясь на 1)–22), в [7, 8, 9] было доказано, что в левой IPVW-системе характеристики 2 из a(b + 1) = ab + a следует a(b + c) = ab + ac, V a, b, c. Следовательно, из 7 з следует 23).

24): Опираясь на теорему Линника 1.2 и 1)–23), заключаем, что тернар бесконечной плоскости Фано представляет собой альтернативное, и следовательно, ассоциативное тело характеристики 2.

Доказана импликация 7 з ^ 24), а затем и теорема 2.8. B

Тем самым получено положительное решение проблемы Аргунова — Глисона: из вышеизложенного следует, что всякая проективная плоскость Фано дезаргова.