Решение проблемы Рашевского

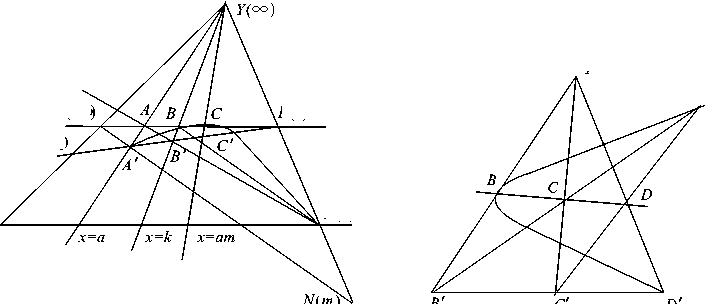
Рассмотрим частный случай теоремы Дезарга, а именно следующую конфигурационную теорему (рис. 1).

Если для трехвершинников 12 3 и 1 0 2 0 3 0 существует центр 4 перспективы, стороны одного инцидентны вершинам другого и точки 5, 6, 7 пересечения сходственных сторон инцидентны одной прямой, то (4, 5, 6, 7) .

Эту теорему, имеющую ранг 7 и состоящую из 10 точек и 10 прямых, обозначим через L(7;10;10) = L 7 [4].

Выясним связи между L 7 и нижеследующими конфигурационными теоремами Рашевского 8 3 и 13 4 [2].

Теорема 1 (К. Теорема 8 3 (рис. 2) [2] ). Если B, C, D — точки одной прямой, перспективно связаны с точками B ⁰ , C ⁰ , D ⁰ другой прямой, то после круговой подстановки над B ⁰ , C ⁰ , D ⁰ перспективное соответствие сохраняется.

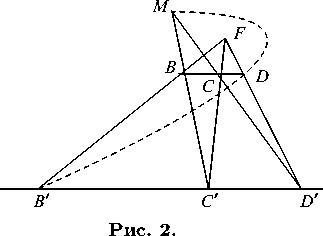
Теорема 2 (К. Теорема 13 4 (рис. 3) [2] ). Если для точек B, C, B 0 , C 0 общего положения и точек A = [B,C] A [B 0 ,C 0 ] , P = [B,C ⁰ ] A [B 0 ,C ] , Q = [A, P] A [C, C 0 ] , D = [B ⁰ , Q] A [C,B] , D' = [B,Q] A [B 0 ,C 0 ] , R = [D, C 0 ] A [C,D 0 ] , F = [C, C 0 ] A [B,B 0 ] , M = [C,D ⁰ ] A [B,C 0 ] , N = [C, B 0 ] A [D, C 0 ] выполняются инциденции (D,D',P,F ) ,

(B,B ' ,R, F) , (P, Q,R, A) , (A, M, N, F) , (B,D ' , Q, N) , то выполняется и замыкающая ( d,B ' ,Q,M ) (рис. 3).

В [2] доказано, что 8 3 проективно эквивалентна 1З 4 , а конфигурация 1З 4 есть полное свободное расширение 8 3 , т. е. плоскость над QF(3) .

Теорема 3 [4] . В проективной плоскости теорема L 7 эквивалентна теореме 1З 4 и, следовательно, теореме 8 3 .

C Доказательство теоремы 3 разобьем на четыре леммы.

Лемма 1. 1З 4 ^ L 7 (рис. 1, 3).

C Рассмотрим два трехвершинника AC ' C и FBD ' с инциденциями FI [C, C 0 ] , BI [A, C ] , D' I [A, C 0 ] , M = [A, F ] n [C ' ,B] n [C, D ' ] , B = [A, C 0 ] n [F, B ] , D = [A, C] n [F, D ' ] , Q = [C, C ' ] П [B,D ' ] и докажем (M, D, B ' , Q), исходя из 13 4 . С этой целью выберем в L 7 следующие четыре точки общего положения B, C, B ' , C ' и построим 13 4 по вышеуказанной таблице инциденций. Тогда в силу выполнения 13 4 в плоскости в ней имеет место инциденция (M, B 0 ,D,Q) ^ L 7 . Отсюда следует также, что L 7 вложена в 13 4 . B

Лемма 2. L 7 ^ 13 4 •

C Докажем, что из L 7 следуют все инциденции 13 4 . С этой целью рассмотрим в 13 4 шесть пар трехвершинников:

• (I)    = {BB ' Q; C ' CA } ,                    (II) = {CC ' P ; D ' DA } ,

• (III)    = {MCО ; FD ' B } ,                (IV) = {NCО ; FB ' D } ,

• (V)    = {CC ' M; PRF } ,                  (VI) = {CC ' N; RPF } .

Учитывая, что в QI [C, C ' ], BI [C, A], B ' I [C ' , A] , P = [B ' ,C ] П [B,C ' ] П [A, Q] , прямая [F, D ⁰ ] , где F = [B, B ⁰ ] n [C, C ⁰ ] , D ⁰ = [B, Q] n [C ⁰ , A] , инцидентна P , то заключаем, что для трехвершинников (I) выполняются условия L 7 и, следовательно, выполняется и замыкающая инциденция (P, F, D, D ⁰ ) , где D = [B ⁰ , Q] n [C, A] , или, другими словами, трехвершинники (I) в 13 4 порождают конфигурацию L 7 . Этот факт запишем так: (I) ^ (P, F, D,D ' ) . Аналогичными рассуждениями при учете (P, F, D, D ' ) устанавливаем, что (II) ^ (P, A, R) и (F, R, B, B' ) . Далее, сравнивая (P, A, Q) и (P, A, R) , заключаем (P, A, Q,R) . Если учесть, что в (III) FI [C, C ' ], D'I [M, C ] , BI [M, C ' ] и точки P = [M, C ' ] n [F, D ' ] , R = [M, C] n [F, B] , Q = [C, C ' ] П [D ' , B] лежат в силу (II), на одной прямой (оси перспективы), A = [C , D ] n [C, B] лежит на оси, то заключаем, что (A, F, M) . Далее имеем, что (IV) ^ (A, F, N ) . Сравнивая последние две инциденции, мы приходим к (A, M, N, F ) . Опираясь на рассуждения, аналогичные предыдущим, заключаем, что (V) ^ (B,D ' Q,N) . Так как в (VI) FI [C, C ' ] , PI [C, N] , RI [C ' ,N ] , (Q,B ' ,D) , где Q = [C ' ,C ] П [P,R] , B ' = [C,N ] П [R, F] , D = [C ' ,N ] П [P,F ] , M = [C, R] П [C ' ,P ] П [N, F ] в силу предыдущих инциденций, то (D,Q,M,B ' ) . Итак, из L 7 следуют все инциденции теоремы 13 4 . B

Лемма 3. 8 3 ^ L 7 .

C Пусть трехвершинники 12 3 и 1' 2Х 3' имеют центр 4, точками пересечения сходственных сторон будут точки 5, 6 и 7 и вершины одного лежат на сторонах другого. Докажем 83 ^ (4, 5, 6, 7). С этой целью рассмотрим в L7 пару коллинеарных троек 2 3 5 и 7 2 3' с центром перспективы в точке 1'. В силу 83 тогда пара 2Х3 5 и 2 3'7 также перспективна с центром в [2 , 3] П [2, 3х] =4. Следовательно, 83 ^ (4, 5, 7). Аналогичному этому, из перспективности пары 4 101 и 306 20 с центром в 3 в силу 83 следует перспективность пары 4 101 и 6 2030 с центром в [10, 20] П [2, 30]. Итак, 83 ^ (4, 6, 7). B

Лемма 4. L 7 ^ 8 3 .

C В L 7 выделим пару коллинеарных и перспективных троек 2 0 3 5 и 7 2 3 0 (см. рис. 1) с центром 1 0 = [2 0 , 7] П [3, 2] П [5, 3 0 ] . Так как в L 7 точки 4, 5 и 7 коллинеарны, то тройки 2 3 5 и 2 3 7 перспективны с центром в 4 = [2 ,2] П [3, 3 ] П [5, 7] . Это значит, что 8 3 , порожденная вышеуказанными тройками коллинеарных точек, замыкается. (Заметим, что доказательство импликаций L 7 ^ 8 3 и 8 3 ^ L 7 в силу результатов Рашевского 8 3 ^ 13 4 , 13 4 ^ 8 3 могут быть опущены, как следствия из L 7 ^ 13 4 и 13 4 ^ L 7 .) B

Теорема 4. Из 8 3 следует первая малая теорема Паппа.

C Пусть для точек 4, 6, 2 прямой 1 1 и точек 1, 3, 5 прямой 1 2 плоскости Рашевского выполняются инциденции:

7 = [1, 6 П [3,4], 8 = [3, 6] П [2,1], [4, 8] П [1, 3] = 5, 9 = [5, 6] П [3, 2], тогда выполняется и инциденция (7, 8, 9).

Докажем соотношение 8 3 ^ (7, 8, 9) (рис. 4).

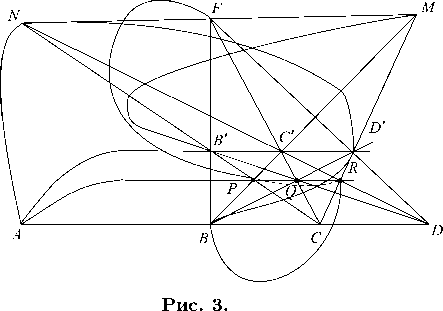
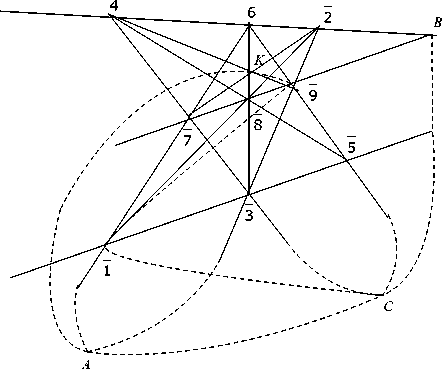
Рис. 4.

1)_L7 { 3 4_2;_6 9 7 } : (3,4, 7),_ (3, 2, 9), (2,4, 6) , K = [3, 6] П [2,7] П [4,9] , A = [2, 3] П [6, 7], B = [2,4] П [7, 9], C = [9,6] 0 П [3,4_] ^_( A,B,C,K) ,_ _     _

• 2) Рассмотрим точки 8 = [3, 6] П [7, 9] и 8 = [3, 6] П [4, 5] П [1, 2] и докажем их совпадение

нижеследующим образом:

• (2.1)    83 ( 7 3 с )’ [6,7] П [2,3] П [B,C ]= A ^( 3  C  B ), [6,3] П [2, C ] П [B, 7] =

8 0 , 8 = [3, 6] П_[ B_L7,9], (2, C, 8 0 ); (3,6, 8 0 ) ;               _  _  _

• (2.2)    83 ( 7 9 8 0 }, [4, 7] П [6, 9] П [2, 8] = C , (9   8 0   7 ), [4, 9] П [6, 8 0 ] П [2, 7] = K ;

(6, 8 0 , K), 8 0 = [2, C] П [3, 6] П [7, 9, B] П [6, K] ^ (K, 6, 3, 8 0 ) ;

• (2.3)    83 ( 1 K B ), [1,7] П [K, 3] П [2,B] = 6, K ( B K 3 )’ [7,B] П [1,K ] П [2,3] = 9, (9,1,K, 4), (1,4, 9) ;

  [3, 6] П [4, 9], (K, 4, 9) ,

  
  

• (2.4)    8з( 7 8 0 9 }, [1, 7] П [3, 8 0 ] П [5, 9] = 6 , Q 7 8 0 ), [1, 9] П [7, 3] П [8 0 , 5] = Q, 4 = [1,9,4] П [3, 7,4] = Q л (5,4, 8 0 ) , 8 0 = [4, 5] П [7,9] П [3,6], 8 = [3,6] П [4, 5] л 8 0 = 8 л (7, 8,9) . B

Следствие 4 0 . В тернарном кольце плоскости Рашевского операция сложения (+) подчиняется аксиомам абелевой группы, т. е. из 8 3 следует выполнение аксиом абелевой аддитивной группы. (Доказательство предложения 4 0 следует из теоремы 4 и теоремы Рашевского — Аргунова [1, 2] : «Из проективного выполнения первой малой теорема Паппа (Щ) следует выполнение аксиом аддитивной абелевой группы в тернаре плоскости».)

Теорема 5. L 7 л a + a + a = 0 при любом a.

C Пусть образующие точки L7 имеют координаты: 1 = (0), 2 = (0, 0), 3 = (a, a), 4 = (го) (см. рис. 5), тогда:

• 1 0    = [4,1 П [2, 3] = U П [y = х] = (1) ,

2 0 = [4, 2] П [1,3] = [х = 0] П [y = a] = (0, a) ,

3 0 = [4, 3] П [1, 2] = [х = a] П [у = 0] = (a, 0) ,

• 5    = [1, 2] П [1 0 , 2 0 ] = [у = 0] П [у = х + a] = ( - a, 0) ,

• 6    = [1, 3] П [1^х, 3^х] = [у = a] П [у = х — a] = (a + a, a) ,

• 7    = [2, 3] П [2 0 , 3 0 ] = [у = х] П [у = х • f о a] = (х г ,у г ) = (x r , х г • f ◦ a) = (x r , Х 7 ) ,

• 3    • I ^^ 0 = a • f о a Л — a = af, a = — af, a • f о ( — af) = 0 при любом a .

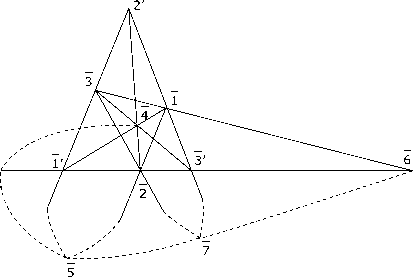
Рис. 5 ( L 7 ) .

Отсюда f = —1 и a(—1) = —a.(

• (5, 6, 7,4) ^^ х б = х 5 ^^ — a = a + a = х г Л

a + a + a = 0.(

• 7 = (— a, —a) = (— a, (— a)(—1) о a) = (— a, a + a),

(—a) • (—1) о a = a + a = (a)(—1) + a,(

—a = a(—1) = a(1 + 1) ~. Л a + a = a(1 + 1). B

Теорема 6. 8 3 Л a • m о b = am + b при любых a, m, b .

C Пусть в 83 A0 = (a, a • m о b), B0 = (k, k + q), C0 = (am, am + q), k = am + q — b, q = a • m о b — a, B = (k, k + b), C = (am, am + b) (см. рис. 20), тогда:

[B, B 0 ] П [C, C 0 ] = Y = ( го ), A = [Y, A ⁰ ] П [B, C] = [х = a] П [у = х + b] = (a, a + b),

( A B C) ^( A B C M ^{= M n} [B,C 0 ] ⁿ [ c,a ] ,

[A, B0] = [y = x • f о t] IA ^^ a + b = a • f о t, B' I ^^ k + q = k • f о t ^ a + b — k — q = a • f о t — k • f о t ^^

Ya — Ybo = am + b — a • m о b = a • f о t — k • f о t = p,(

[A ⁰ , C ] = [y = x • f 1 о t 1 ] IA ^^ a • m о b = a • f 1 о t 1 , IC ^^ am + b = am • f 1 о t 1 ^

Yc — Yao = am + b — a — a • m о b = am • f1 о t1 — a • f1 о t1 = p,(

[B, C ] = [y = x • f ₂ о t ₂ ] IB ^^ k + b = k • f ₂ о t ₂ , IC ⁰ ^^ am + q = am • f ₂ о t ₂ ^

Y b — Y c o = k + b — am — q = k • f ₂ о t ₂ — am • f ₂ о t ₂ ^^

am — q — b + b — am + q = 0 = k • f2 о t2 — am • f2 о t2 ^

/2 = 0, [B,C0] = [y = k + b] = [y = am + q], Yb — Yc. = 0,(

{(*.1), (*.2)} ^ a • f о t — k • f о t = am • fot1 — a • f1 о t1.(

Уравнение (*.5) при f = fi = 0 сводится к тождеству 0 = 0, уравнения (*.1) и (*.2)

дают: p = am + b — a • m о b = 0 ^^ a • m о b = am + b . B

F e (1)

Q(0,q)

X (0)= M

C

M

Рис. 2 0 (8 3 ) .

0(0, (0,0)

t (0, b)

Рис. 6.

Теорема 7. 8 3 ^ ( — a — b)r = — ar — br при любых a, b, r.

C Пусть в 8 3 B ⁰ = (a, ar), C ⁰ = (b, br) , D = ( — a — b, (—a — b)r), C = (b, ar), D = ( — a — b, (—a—b)r — br +ar) (см. рис. 6), тогда: F = CC ⁰ П DD = [x = b] n [x = —a — b] = ( ro ) , B = FB П CD = [x = a] n [y = xr — br +ar] = (a, — ar — br) , M = B ⁰ C П C ⁰ D = [y = ar] n [y = xf + t] , C ⁰ 1 ^^ br = bf + t ^ t = br — bf , DI ^^ ( — a — b)r — br + ar = ( — a — b)f + t .

( — a — b)r — br + ar = ( — a — b)f + br — bf,

(—a — b)r — br + ar = (—a — b)f — bf.(

BD ⁰ = [y = x^ + t ⁰ ], BI ^^ — ar — br = a^ + t ⁰ , DI ^^ ( — a — b)r = ( — a — b)^ + t ⁰ ,

(—a — b)r + ar + br = (—a — b)^ — a^.(

• { ( * .1), ( * -2) } ^ ( — a — b)^ — a^ = ( — a — b)f — af ^ ^ = f ^ C ⁰ D n BD = M = (f) ,

BC = [y = ar] = [y = x • 0 + ar] I (0), B'C n l^ = (0), M = C'D n B0C n BD0

[y = xf + t] n [y = x • 0 + ar] n [y = xf + t0] = (0) = (f) = (y).(

• { ( * .1) — ( * -3) } ^ ( — a — b)r = — ar — br . B

Следствие 7 0 . Из теоремы 7 следуют:

• (1)    ( — a)b = (a + a)b = ab + ab = —ab;

• (2)    (—a — b)r = -ar — br = ( — a)r + ( — b)r ^ —a = k, —b = p, (k + p)r = kr + pr при любых k, p, r .

Теорема 8. 8 3 ^ a(b + c) = ab + ac при любых a, b, c.

C (рис. 6). Пусть в 8 3 B ' = (0,0), C’ = (—a, —a(b + c)), D = (a,a(b + c)), D = (a, —ab — ac), C = ( — a, 0) , тогда: F = CC* n BB’ = ( ro ), DC = [y = xq + t] IC =^ 0 — aq + t ^ t = aq, DI =^ —ab — ac = aq + t = q + a = —aq =^ aq = ab + ac, DC = [y = xq + aq], B = CD n FB' = [y = xq + aq] П [x = 0] = (0, aq) = (0, ab + ac), M = B ' C n C'D n BD = [y = 0] П [y = xf + t i ] П [y = xf ₂ + ab + ac] , C ' I =^ —a(b + c) = —af i + t i , DI =^^ — ab — ac = af i + t i ,

—a(b + c) + ab + ac = —afi — af = afi, a = 1, fi = 0,(

D ' I =^ a(b + c) = af ₂ + ab + ac,

a(b + c) — ab — ac = af2 =^ при a = 1, f2 = 0,(

{(*•1), (*.2)} ^ afi + af2 = 0 Va = 0.(

Тривиальное решение f i = f = 0 уравнения (*.3) относительно f i и f приводит к равенству

a(b + c) = ab + ac.(